Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

2.4 Uniform, exponential, and Gaussian distributions 27

(

)

min

max

∆

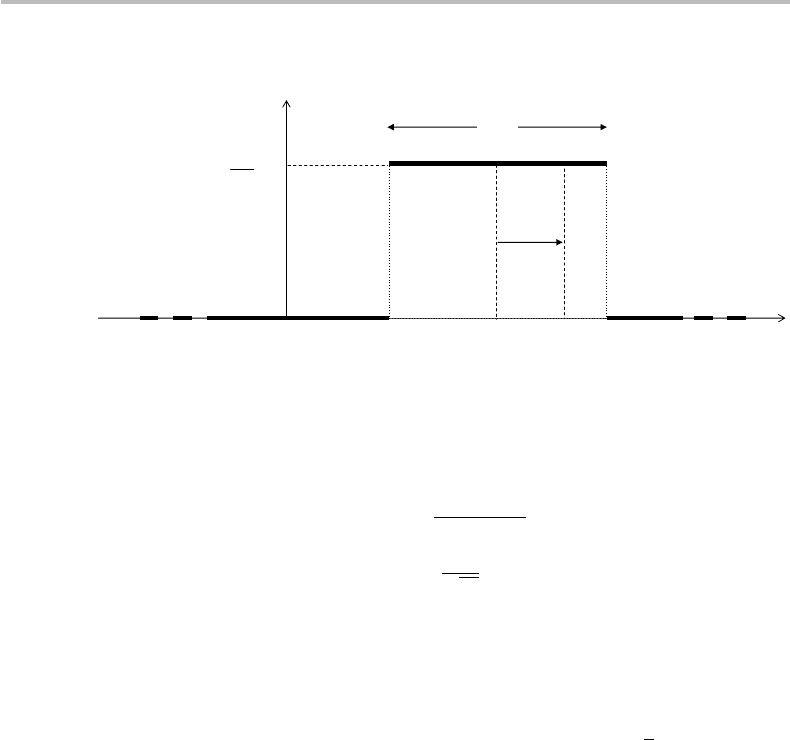
Figure 2.5 Uniform probability distribution of the continuous variable x, see text for description.

identically zero outside the relevant sample interval

[

min

, x

max

]

.Itisleftasanexer-

cise for the reader to show that the mean and standard deviation of a continuous,

uniform PDF are:

<x> ==

max

+ x

min

, (2.15)

σ =

x

√

. (2.16)

We see from the above results that for a uniform PDF the mean <x> corresponds to the

mid-point (x

max

+ x

min

)/2 of the interval

[

min

, x

max

]

. This was expected, since all events

x in this interval are equally probable. However, the deviation σ is different from the

half width of the distribution, x/2, which was not intuitive! This is because (as deﬁned

earlier, and to recall) the variance is the mean value of the square of the difference

x − <x>, i.e., σ

= <(x − <x>)

>. Thus, the quantity 2σ = x/

√

3 does not deﬁne a

speciﬁc interval where the continuous events x are more likely to be observed, although

the contrary is true for most other types of nonuniform PDF.

Uniform continuous distributions, which take the shape of square or step functions, are

not generally found in the physical world. One remarkable example, however, is provided

by the so-called Fermi function in semiconductors while under absolute-zero temperature

(T = 0 kelvin). Such a function is the probability f (E) of having an electron at a given

energy E. The physics shows that, at zero temperature, f (E) = 1/E

for 0 ≤ E ≤ E

and f (E) = 0forE ≥ E

, where E

is referred to as the Fermi energy level. To

take a simpler example, assume that one is able to measure some physical parameter

within an absolutely deﬁned range. For instance, the distribution of frequencies F from

microwave or sunlight radiation, as analyzed through a perfect, square-shaped bandpass

ﬁlter (suppose that measurements outside that ﬁlter range are not observed or irrelevant

to the test). If the ﬁlter is not too large (or is sufﬁciently narrow!), and under some

circumstances, then one may, indeed, observe that the measurement probability p(F)is

uniformly distributed. In any case, this would not mean that the probability is uniform

in the absolute deﬁnition, but in a local-domain sense, as deﬁned by the observation

window of measurement apparatus.

28 Probability distributions

Next, we consider the continuous-exponential distribution. The PDF is deﬁned for

x ≥ 0 as follows:

p(x) = λe

−λx

, (2.17)

where λ is a strictly positive constant called the rate parameter. The mean and variance

of the exponential PDF are <x> = 1/λ and σ

= 1/λ

, respectively (this is left as an

exercise).

Between the discrete-exponential and the continuous-exponential PDFs, there is no

one-to-one correspondence, except in the limit of large means. Indeed, setting N = 1/λ

in Eq. (2.17), we can redeﬁne the discrete-exponential PDF (x = n integer) under the

form

p(n) =

λ + 1

−n log(1+λ)

. (2.18)

Such a deﬁnition corresponds to that of the continuous PDF (Eq. 2.17) only in the limit

λ → 0 (for which log(1 + λ) → λ), which corresponds to the limit N →∞.

The continuous-exponential PDF is used to model the timing of physical events that

happen at a constant average rate. If x = t is a time variable, the event occurs at exact

time t with probability p(t) = λ exp(−λt). We note that in this case, λ has the dimension

of an inverse time (e.g., inverse seconds or inverse days), meaning that the PDF is a

probability rate (in /s or /day units) rather than being dimensionless. The exponential

PDF is a maximum for t = 0 and decays rapidly as time increases. On average, the

events occur at time <t> = 1/λ ≡ τ , where τ is a characteristic time constant.In

atomic physics, τ is called the decay constant, or also the 1/e lifetime. For radioactive

atoms or for atoms used in laser materials, this means that the disintegration or photon

emission occurs in average at the time t = τ . The probability that any atom decays at a

time after t is given by

p(T > t) =



+∞

p(t



)dt



+∞

τ exp(−t



/τ )dt



(2.19)

= τ



−

exp(−t/τ )



+∞

= exp(−t/τ ).

The integration expresses the fact that the probability p(T > t) is given by the continuous

sum of all probabilities p(t



) where t



belongs to the time interval

[

t, +∞

]

. The result

shows that the probability that any atom decays after t = τ is p(T >τ) = e

−1

= 1/e ≈

0.36, hence the name 1/e lifetime. The probabilities that atoms decay after times t =

2τ,3τ,..., etc., are 13%, 5%, etc., illustrating that there is always a ﬁnite number of

“surviving” atoms remaining in their original state and awaiting decay, but their number

decreases exponentially over time.

Other applications of the exponential PDF can be found in daily life. For instance, if

a person regularly drives above the speed limit and if the highway patrol makes regular

controls, the probability of getting a speeding ticket only after a given time t, i.e.,

p(T > t) = exp(−t/τ ), is rapidly vanishing, just like the drivers’ luck. The probability

that he or she will get a ticket before time t, i.e., p(T < t) = 1 −exp(−t/τ ), is rapidly

2.4 Uniform, exponential, and Gaussian distributions 29

increasing towards unity, representing a situation reaching 100% likelihood. If τ = 1

year represents the mean time for bad drivers to get a speeding ticket, the probability of

only getting a ticket 2 to 3 years after that time is only 13% to 5%, meaning that there

is an 87% to 95% chance of getting it well before then!

The exponential distribution is also used to characterize reliability and failure in

manufactured products or systems, such as TV sets or car engines. Given the mean time

to observe a given failure, τ (now called mean time to failure or MTTF), the probabilities

that the failure will be observed before or after time t are p(T <t) = 1 − exp(−t/τ )or

p(T >t) = exp(−t/τ ), respectively. The function p(T >t) is generally referred to as the

reliability function. Its complement, p(T <t) = 1 − p(T >t) is referred to as the failure

function. For instance, if τ = 5 years represents the mean time to get a car-engine

problem, the probability of getting the problem within one year is p(T <1 year) =

1 − exp(−1/5) = 0.18, and after one year p(T >1 year) = 1 − p(T < 1 year) = 0.82.

This means that there is close to a 20% chance of having the problem before one year,

even if the car engine (or driving safety) is supposed to be problem-free for a mean

period of 5 years. On the other hand, the odds of having a problem after one year are

82%, but this prediction covers an inﬁnite amount of time. It is possible to make a more

detailed failure prediction for a given period spanning times t

to t

> t

. Indeed, the

probability of getting a failure between these two times is:

p(t

< T < t

) = 1 −

[

p(T < t

) + p(T > t

)

]

= 1 −

[

1 − exp(−λt

) + exp(−λt

)

]

(2.20)

= exp(−λt

) − exp(−λt

With the above formula, one can determine the failure probabilities concerning any

speciﬁc periods deﬁned by

[

, t

]

Next, we consider as a last but key example, another continuous PDF, which is the

Gaussian or normal distribution.Withamean<x> = N and a variance σ

,itisformally

deﬁned according to:

p(x) =

√

2π

exp



−

(x − N )

2σ



. (2.21)

Since the function exp(−u

) is symmetrical with a peak value centered at u = 0, we

see that the Gaussian PDF is centered about its mean, <x> = N , with a peak value of

p(N ) = p

peak

= 1/(σ

√

2π). For values x = N ± σ

√

2, we observe from the deﬁnition

that the probability drops to e

−1

peak

= p

peak

/e ≈ 0.367p

peak

. Figure 2.6 shows plots of

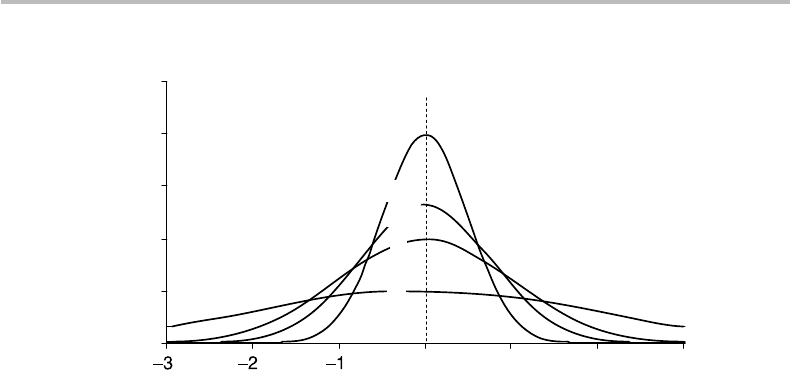
Gaussian PDFs with mean N = 0 and different standard deviations.

The characteristic bell shape has justiﬁed over time the popular name of bell distri-

bution, which is well known to a large public. The surface S under the curve, which is

deﬁned by two points x

, x

, i.e.,

S = p(x

<x<x

) =



p(x)dx, (2.22)

represents the probability of event x taking a value in the interval

[

, x

]

. It can be

shownbyintegrationinEq.(2.22) that p(N − σ<x < N + σ ) ≈ 0.682, meaning that

30 Probability distributions

0.2

0.4

0.6

0.8

3210

(

)

> =

0.75

0.5=

Figure 2.6 Gaussian probability distribution with mean <x > = N = 0 and standard deviations

σ = 0.5, 0.75, 1, and 2.

68.27% of the bell surface concerns events falling within two standard deviations (±σ )

of the mean (N). Likewise, for the intervals 2σ and 3σ about the mean, the surfaces

represent 95.4% and 99.7 of the total bell surface, respectively.

A physical parameter obeying a Gaussian PDF, for instance, electrical noise in radio

or TV signals, is experimentally characterized through discrete sampling, even if the

measurement apparatus (e.g., an analog oscilloscope) provides a continuous signal. It

is interesting to see what a succession of such sampling measurements looks like in

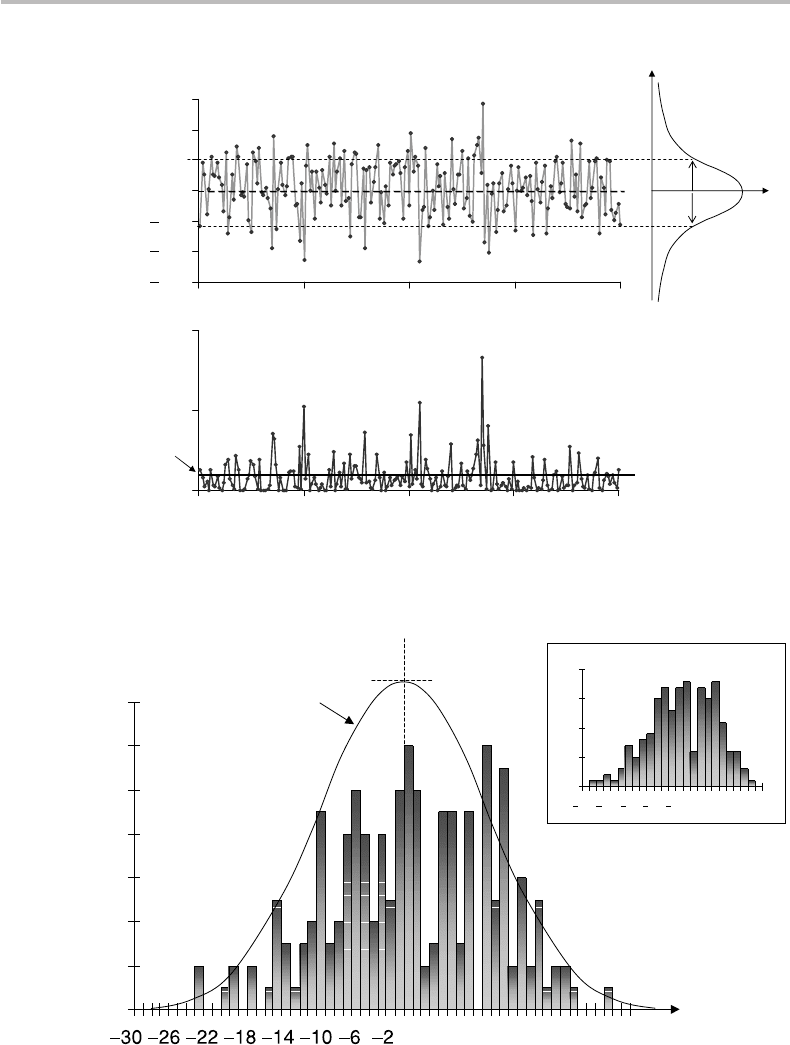
the real world. Figure 2.7 shows the plot of a series of 200 samplings of a random

variable x following a Gaussian distribution with <x> = 0 and σ = 0.1, as generated

by a computer program. We observe that, as expected, the values of x are randomly

distributed above and below the x axis. The sampling points form a cloud that is denser

near the axis, deﬁning a region of width 2σ . The ﬁgure also includes the corresponding

plot of x

, which shows that most of the sampling points are found between x

= 0

and x

= <x

> = σ . It is important to distinguish the discrete sampling points (here

numbering 200) from the continuous, Gaussian PDF. To compare the two, we can draw

a histogram of the sampling points, as shown in Fig. 2.8. The histogram represents the

counts of points corresponding to the different values of x in Fig. 2.7. For clarity, I have

multiplied the sampled variable x by a hundredfold and truncated the result (y = 100x)

to an integer, which gives values ranging from y =−23 to y =+29.

As seen from Fig. 2.8, the envelope of the histogram is quite different from that

of the actual Gaussian distribution, also plotted in the ﬁgure for comparison (with

= 100 × σ

= 10). The reason for this discrepancy is twofold. First, once gathered

into a histogram, the discrete samplings do not have a sufﬁcient number (here 200) to

reproduce the smooth and continuous features of the Gaussian PDF. Second, the data

were arbitrarily arranged into truncated integer bins, which enhances the discontinuity

of the histogram’s envelope. To show how this truncation changes the envelope, a second

histogram was made with z = 50x (see inset in Fig. 2.8). This second histogram has

a smoother envelope, because there are more data in each of the integer bins. For this

2.4 Uniform, exponential, and Gaussian distributions 31

0.1

0.2

0.3

0.1

0.2

0.3

200150100500

(x)

< x >

0.00

0.05

0.10

200150100500

Figure 2.7 Example of discrete samplings (200 events) of a Gaussian distribution

(<x > = 0,σ = 0.1), showing the outcome for random variables x (top) and x

(bottom).

2 6 9 13 17 21 31

Counts

(

)

y =

100

2471013 1 5 8 15

0.04

z =

Figure 2.8 Histogram of the 200 sampling points x shown in Fig. 2.7, as converted into

y = 100x, and corresponding Gaussian distribution envelope p(y). The inset shows a denser

histogram corresponding to the same x data with z = 50x.

32 Probability distributions

reason, the envelope shape is closer to that of a bell. To obtain a smooth histogram

envelope that would closely ﬁt the Gaussian bell curve, one would need to acquire

–10

sampling points and arrange them into hundreds of histogram bins.

The lesson learnt is that experimental statistics require large numbers of samplings

in order to reﬂect a given probability law, for instance, the Gaussian PDF (but it is not

limited to this case). We have previously reached a similar conclusion from our earlier

coin-ﬂipping experiment, for which the associated probability distribution is discrete

and quite elementary ( p(heads) = p(tails) = 1/2), see Chapter 1 and Fig. 1.3. To recall,

it took no less than 700 samples to approach the expected uniform distribution with

reasonable accuracy.

The Gaussian or normal probability distribution characterizes a large variety of ran-

dom processes found in physics, in engineering, and in many other domains of science.

In most random processes indeed, the uncertainty associated with continuous param-

eters, which is also referred to as noise, obeys a Gaussian (normal) PDF. Here is a

nonlimitative list of Gaussian (normal) processes:

Experimental measurement errors (the mean <x> being taken as the value to be

retained);

Manufacturing, in the distribution of production yields and quality scoring;

Telecommunications, in the distribution of 1/0 bit errors in digital receivers;

Photonics, to approximate the transverse or spatial distribution of light intensity in

optical ﬁbers or in laser beams;

Education and training, in the distribution of intelligence (IQ) test scores, or profes-

sional qualiﬁcations and performance ratings;

Information theory, which will be developed in Chapter 4 when analyzing continuous

channels with noise.

Medicine, in the distribution of blood pressure and hair length, or of the logarithm of

body weight or height;

Economics and ﬁnance, in the distribution of the logarithm of interest rates, exchange

rates, stock returns, and inﬂation.

Processes that are associated with a Gaussian (normal) distribution are said to respond

to normality. If normality is satisﬁed only with the logarithm of the variable x (as seen

in the last two above examples), the process is said to be log-normal.

By way of a

simpliﬁed explanation, normality comes from the additive effect of independent random

factors, while log-normality comes from their multiplicative effect.

Generally, the Gaussian (normal) law represents a good approximation of most con-

tinuous distributions, provided the number of events or samples is relatively large. This

will be shown in the next section. Furthermore, the Gaussian (normal) law represents

the asymptotic limit of most discrete probability distributions with large mean <k>,

two key examples being the binomial and the Poisson PDFs described in the previous

section. As we have seen, the binomial distribution p

= C

(1 − q)

n−k

, which is

For advanced reference, the log–normal distribution is deﬁned as: p(x) =

xσ

√

2π

exp



−

(

log x−µ

)



.Its

mean and variance are N = exp(µ + s

/2) and σ



exp





− 1



exp



2µ + s



, respectively.

2.5 Central-limit theorem 33

deﬁned for integers k = 0,...,n,Eq.(2.9) converges towards the Poisson distribution,

Eq. (2.8) in the limit of large n. In the same limit, it can be shown that both distri-

butions converge towards a Gaussian (normal) PDF of same mean <k> and variance

= nq(1 − q).

2.5 Central-limit theorem

In probability theory, there exist several central-limit theorems, which show that the sum

of large numbers of independent random variables, each having a different probability

distribution, asymptotically converges towards some kind of limiting PDF.

Remarkably, this limiting PDF is the same, regardless of the initial distribution of

these variables. The most well known of these theorems is referred to as the central-limit

theorem (CLT). The CLT states that if the variance of the initial distribution is ﬁnite,

the limiting PDF is the Gaussian (normal) distribution. The CLT thus explains why the

Gaussian (normal) distribution is found in so many random processes: such processes

usually stem from the additive effect of several independent or uncorrelated random

variables, which individually obey any PDF type.

A simpliﬁed formulation of the CLT is as follows. Let x be a random variable of a

given parent distribution p

parent

(x). The parent distribution is characterized by a mean

<x> = N and a ﬁnite variance σ

.Letx

, x

,...,x

be a series of k independent

samples from this distribution. Deﬁne the sum

= x

+ x

+,...,x

. (2.23)

Since the random variables (or samples) are independent, the mean and the variance of

the sum in Eq. (2.23)are<S

> = kN and σ

= kσ

, respectively.

The CLT simply states that the probability distribution of S

asymptotically becomes

Gaussian (normal) as the number of samples k increases,ork →∞. A more general

formulation of the CLT assumes a set of independent random variables X

,...,X

Each of these variables X

has a different probability distribution p

(x). Each distribution

(x) has a mean N

and a variance σ

. Deﬁne the sum S

= X

+ X

+,...,X

. Since

the variables X

,...,X

are independent, the mean and variance of the sum are

> = N

+ N

+,...,N

and σ

= σ

+ σ

+,...,σ

, respectively. Just as in the

previous formulation, the CLT simply states that the probability distribution of the sum

is asymptotically Gaussian (normal).

I will not expand on the formal proof of the CLT, which is beyond the scope of

this book.

However, for both clariﬁcation and fun purposes, the reader might check

up this proof through some nicely illustrated online experiments using interactive Java

Formal demonstrations of the CLT can be found in many academic books and in some websites. See, for

instance: http://mathworld.wolfram.com/CentralLimitTheorem.html.

34 Probability distributions

applets.

I consider here an experimental example of CLT proof, using one such web

tool.

Rolling dice and adding spots

This is an experiment similar to that described earlier in Chapter 1 and illustrated in

Figs. 1.1 and 1.2. As we know, each individual die has a uniform discrete distribution

deﬁned by p(x) = 1/6 with x

= 1, 2, 3, 4, 5, 6 being the event space. If we roll two

dice and sum up the spots, the event space is x

= 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and the

probability distribution has a triangular (or witch’s hat) shape centered about <x> = 7,

see Fig. 1.2. Interestingly, the CLT does not apply to the two-dice case, the limiting

PDF being still the witch hat, as can be easily veriﬁed. As a simpliﬁed explanation, this

is because the event space is too limited. But when using three dice or more, the CLT

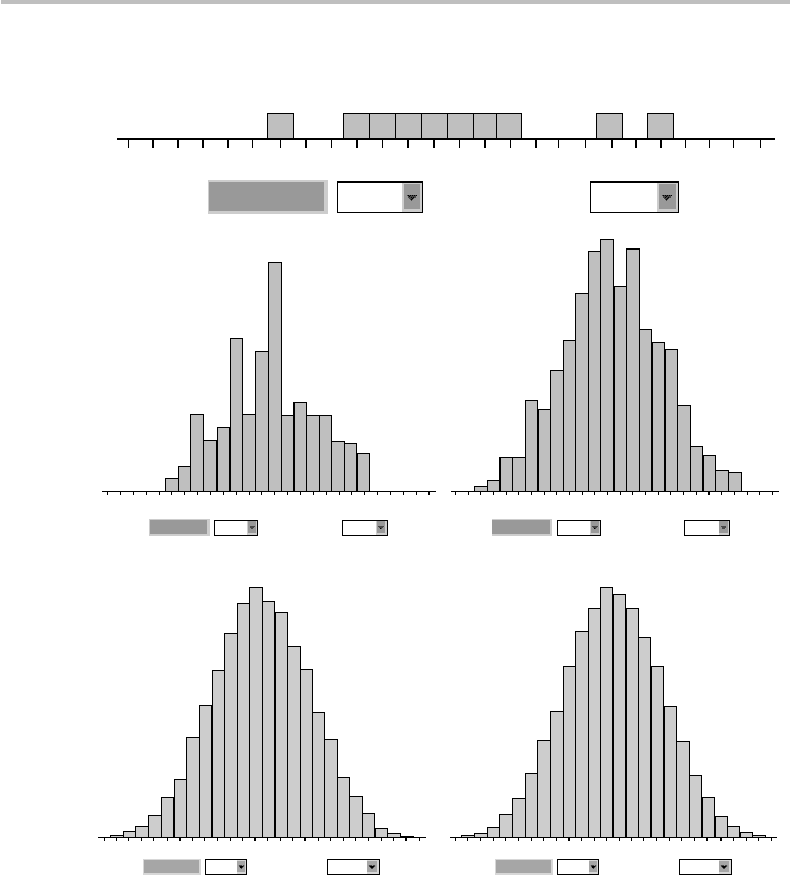
is observed to apply, as illustrated in Fig. 2.9. The ﬁgure shows results obtained with

ﬁvedicefork = 10, 100, 1000, 10 000, and 100 000. It is seen that as k increases, the

resulting histogram envelope progressively takes a bell shape. Ultimately, the histogram

takes a symmetrical (discretized) bell shape limited to the 26 = 30–5+ 1 integer

bins of the event space. A 1000-dice experiment with an adequate number of trials k

would yield a similar histogram with 5001 = 6000 − 1000 + 1 discrete bins, which

is much closer to the idea of a smooth envelope, albeit the resulting PDF is discrete,

not continuous. Only an inﬁnite number of dice and an inﬁnite number of rolls could

provide a histogram match of the limiting Gaussian (normal) envelope.

To complete the illustration of the CLT, consider the school game of a pegboard matrix,

also known as a pinball machine, bean machine, quincunx, or Galton box, and whose

principle is at the root of the Japanese gambling parlors called Pachinko. At each step

of the game, a ball bounces on a peg (or a nail) to choose a left or right path randomly,

according to a uniform, two-valued distribution. The triangular arrangement of pegs or

nails makes it possible to repeat the ball’s choice as many times as there are rows (n)

in the matrix. At the bottom and after the ﬁnal row, the ball rests in a single bin, which

is associated with some reward or gain. It is easily established that the probability for

the ball to be found in a given bin k follows the binomial distribution, Eq. (2.9). If the

number n of rows becomes large, and for a sufﬁciently large number of such trials,

the histogram distribution of balls into the bottom bins takes a Gaussian-like envelope,

which represents a nice, mechanical schoolroom illustration of the CLT.

This concludes the second chapter on probability basics. Most of the mathematical

tools that are required to approach information theory have been described in these two

chapters.

See, for instance:

www.stat.sc.edu/∼west/javahtml/CLT.html,

www.rand.org/statistics/applets/clt.html,

www.math.csusb.edu/faculty/stanton/m262/central

limit theorem/clt old.html,

www.ruf.rice.edu/%7Elane/stat

sim/sampling dist/index.html,

www.vias.org/simulations/simusoft

cenlimit.html.

I am grateful to Professor Todd Ogden for permission to reproduce the simulation results obtained from his

web tool in www.stat.sc.edu/∼west/javahtml/CLT.html.

2.6 Exercises 35

5 10 15 20 25 30 5 10 15 20 25 30

10 15 20 25 30

1000

100