Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

1.1 Events, event space, and probabilities 7

100

150

200

250

300

350

0 100 200 300 400 500 600 700

Number of trials

Count

Heads

Tails

0 100

(a)

0.4

0.5

0.6

0 100 200 300 400 500 600 700

Number of trials

Probability

Heads

Tails

(b)

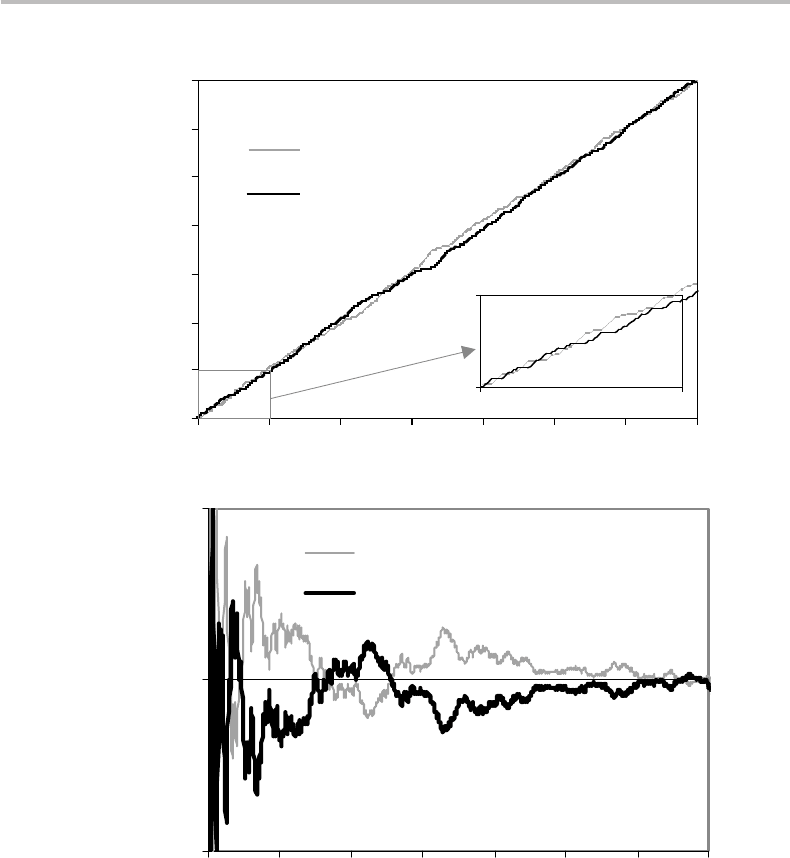
Figure 1.3 Experimental determination of the probability distribution of coin ﬂipping, by means

of 700 successive trials: (a) cumulative count of head and tails outcomes with inset showing

detail for the ﬁrst 100 trials, (b) corresponding probabilities.

themselves as the game progresses, as if the coin would “know” how to come back to

the 50:50 odds rule. Strange isn’t it? The discrepancies between counts are reﬂected

by the wide oscillations of the PDF (Fig. 1.3(b)). But as the experiment progresses,

the oscillations are damped to the point where p(heads) ≈ p(tails) ≈ 0.5, following an

asymptotic behavior.

Performing this experiment and obtaining such results is not straightforward. Different types of coins must

be tested ﬁrst, some being easier to ﬂip than others, because of size or mass. Some coins seem not to lead

8 Probability basics

The above experiment illustrates the difference between event probabilities and their

actual outcomes in the physical world. The nice thing about probability theory is that

the PDF gives one a sense of the unknown when it comes to a relatively large number

of outcomes, as if the unknown, or “chance,” were domesticated by underlying mythical

principles. On the other hand, a known probability gives no clue about a single event,

just a sense of what it is most likely to be. A fair way to conceive of a 10% odds is that

the corresponding event “should be observed” at least once after ten outcomes, and at

least ten times after 100 outcomes, and very close to Q/10 times after Q outcomes, the

closeness being increasingly accurate as Q becomes larger. The expression “should be

observed” progresses towards “should be absolutely certain.” To top off this statement,

we can say that an event with a ﬁnite, nonzero probability is absolutely certain to

occur at least once in the unbounded future. Such a statement is true provided the

physics governing the event (and its associated PDF) remain indeﬁnitely the same, or is

“invariant by time translation” in physicists’ jargon.

1.2 Combinatorics

The examples in the previous section concerned events whose numbers of possible

occurrences in a given trial are easily deﬁned. For instance, we know for certain that a

single die has exactly six faces, with their corresponding numbers of spots. But when

adding spots from two dice (rolling dice, game 2), we had to go through a kind of

inventory in order to ﬁgure out all the different possibilities. While this inventory was

straightforward in this example, in the general case it can be much more tedious if not

very complex. Studying the number of different ways of counting and arranging events is

called combinatorial analysis or combinatorics. Instead of formalizing combinatorics at

once, a few practical examples are going to be used to introduce its underlying concepts

progressively.

Arranging books on a shelf

This is a recurrent problem when moving into a new home or ofﬁce. A lazy solution is

to unpack the books and arrange them on the shelf from left to right, as we randomly

pick them up from the box. How many different ways can we do this?

Answer: Say the shelf can hold ten books, and number the book position from the

left. Assume that the box ﬁts in ten different (or distinguishable) books. The number

of ways to pick up the ﬁrst book to place in position 1 is, therefore, Q = 10. For the

second book to put in position 2, there remain nine possibilities. So far, there have

been Q = 10 ×9 possibilities. Positioning next the third book, the count of possibilities

becomes Q = 10 × 9 ×8. And so on, until the last book, for which there is only a single

to equiprobable outcomes, even over a number of trials as high as 1000 and after trying different tossing

methods. If the coin is not 100% balanced between the two sides in terms of mass, nonuniform PDFs can

be obtained.

1.2 Combinatorics 9

choice left, which gives for the total number of possibilities: Q = 10 × 9 ×8 ×7 ×

6 × 5 ×4 ×3 ×2 ×1. By deﬁnition, this product is called the factorial of 10 and is

noted 10!

More generally, for any integer number n we have the factorial deﬁnition:

n! = n × (n − 1) ×(n − 2) ×···×3 ×2 ×1. (1.6)

Thus

1! = 1,

2! = 2 ×1 = 2,

3! = 3 ×2 ×1 = 6,

and so on. One can easily compute 10! (using, for instance, the factorial function of a

scientiﬁc pocket calculator) to ﬁnd

10! = 3 628 800 ≈ 3.6 million.

There is an impressive number of ways indeed to personalize one’s ofﬁce shelves!

When it comes to somewhat greater arguments (e.g., n = 100), the factorials cannot

be computed by hand or through a pocket calculator, owing to their huge size. To provide

an idea (as computed through a spreadsheet math function up to a maximum of 170!):

50! ≈ 3.0 ×10

100! ≈ 9.3 ×10

157

170! ≈ 7.2 ×10

306

In this case it is possible to use Stirling’s approximation theorem, which is written as

n! ≈ n

−n

√

2πn. (1.7)

Remarkably, the Stirling theorem is accurate within 1.0% for arguments n ≥ 10 and

within 0.20% for arguments n ≥ 40.

To summarize, the factorial of n is the number of ways to arrange n distinguishable

elements into a given orderly fashion. Such an arrangement is also called a permutation.

What about the factorial of the number zero? By convention, mathematicians have set

the odd property

0! = 1.

We shall accept here that 0! = 1 without advanced justiﬁcation. Simply put, if not a

satisfactory explanation, there is only one way to arrange/permute a set containing zero

element.

Consider next a second example.

For the math-oriented reader, it is interesting to mention that the factorial function can be generalized to

any real or even complex arguments x, i.e., x! = (x + 1), where  is the gamma function, which can be

computed numerically.

10 Probability basics

Arranging books on a shelf, with duplicates

Assume that some of the books have one or even several duplicate copies, which can-

not be distinguished from each other, as in a bookstore. For instance, the series of

10 books includes two brand-new English–Russian dictionaries. Having these two in

shelf positions (a, b)or(b, a) represents the same arrangement. So as not to count this

arrangement twice, we should divide the previous result (10!) by two (2!), which is the

number of possible permutations for the duplicated dictionaries. If we had three identical

books in the series, we should divide the result by six (3!), and so on. It is clear, then,

that the number of ways of arranging n elements containing p indistinguishable elements

and n − p distinguishable ones is given by the ratio:

. (1.8)

The above theorem deﬁnes the number of possible arrangements “without repetition”

(of the indistinguishable copies). Consistently, if the series contains n indistinguishable

duplicates, the number of arrangements is simply A

= n!/n! = 1, namely, leaving a

unique possibility.

The next example will make us progress one step more. Assume that we must make

a selection from a set of objects. The objects can be all different, all identical, or partly

duplicated, which does not matter. We would only like to know the number of possibilities

there are to make any random selection of these objects.

Fruit-market shopping

In a fruit market, the stall displays 100 fruits of various species and origins. We have

in mind to pick at random up to ﬁve fruits, without preference. There are 100 different

possibilities to pick up the ﬁrst fruit, 99 possibilities to pick up the second, and so

on until the last ﬁfth, which has 96 possibilities left. The total number of possibilities

to select ﬁve speciﬁc fruits out of 100 is therefore Q = 100 × 99 ×98 ×97 ×96.

Based on the deﬁnition of factorials in Eq. (1.6), we can write this number in the form

Q = 100!/95! = 100!/(100 −5)! But in each selection of ﬁve fruits we put into the

bag, it does not matter in which order they have been selected. All permutations of these

ﬁve speciﬁc fruits, (which are 5!), represent the same ﬁnal bag selection. Therefore, the

above count should be divided by 5! because of the 5! possible redundancies. The end

result is, therefore, Q = 100!/[5!(100 −5)!]. Most generally, the number of ways to

pick up p unordered samples out of a set of n items is

p!(n − p)!

. (1.9)

The number C

, which is also noted (

)or

or C(n, p) is called the binomial

coefﬁcient.

Since the factorial is expandable to a continuous function (see previous note), the binomial coeff-

icient is most generally deﬁned for any real/complex x, y numbers as C

= 

(

x + 1

)



(

)

[



(

x − y + 1

)

]

. Beautiful plots of C

in the real x, y plane, and more on the very rich binomial

1.3 Combined, joint, and conditional probabilities 11

A ﬁnal example is going to show how we can use the binomial coefﬁcient in probability

analysis.

Scooping jellybeans

A candy jar contains 20 jellybeans, of which three quarters are green and one quarter is

red. If one picks up ten jellybeans at random, what is the probability that all beans in

the selection will be green?

Answer: By deﬁnition, the number of ways to pick up 10 green beans out of 15 is C

The total number of possible picks, i.e., a selection of 10 out of 20, is C

. Applying the

probability deﬁnition in Eq. (1.4), with the event being “all picked beans are green,” we

obtain:

p(all green) =

15!

10!5!

10!10!

20!

15!10!

20!5!

(1.10)

10 × 9 ×8 ×7 ×6

20 × 19 ×18 ×17 ×16

= 0.016.

The result shows that the likelihood of getting only green jellybeans is relatively low

(near 1.5%), even if

of the jar are of this type. Interestingly, if the jar had only one

red jelly bean and 19 green ones, the event probability would be p(all green) = 0.5, as

the reader should easily verify. It is also easy to show as an exercise that for a jar of

one red jelly bean and N − 1 green jelly beans, the probability p(all green) becomes

asymptotically close to unity as N reaches inﬁnity, which is the expected result.

1.3 Combined, joint, and conditional probabilities

We have learnt that probabilities are associated with certain events x

belonging to an

event space S ={x

, x

,...,x

}. Here, we further develop the analysis by associating

events from different subspaces of S, and establish a new set of rules for the corresponding

probabilities.

Assume ﬁrst two subspaces containing a single event, which we note A ={a} and

B ={b}, with a, b being included in the space S ={a, b,...}. Let me now introduce

two deﬁnitions:

The combined event is the event corresponding to the occurrence of either a or b or

both; it is also called the union of a and b and is equivalently noted a ∪ b or a ∨ b;

The joint event is the event corresponding to the occurrence of both a and b;itisalso

called the intersection of a and b, and is equivalently noted a ∩ b or a ∧ b.

coefﬁcient properties can be found in http://mathworld.wolfram.com/BinomialCoefﬁcient.html or

www.math.sdu.edu.cn/mathency/math/b/b219.htm.

The symbols ∪ and ∩are generally used to describe union and intersection of sets, while the symbols ∨ and

∧apply to logical or Boolean variables.Ifa is an element of the event set, then the Boolean correspondence

is “event a = veriﬁed or true” For simplicity, I shall use the two notations indifferently.

12 Probability basics

(b)

(a)

∪

∩

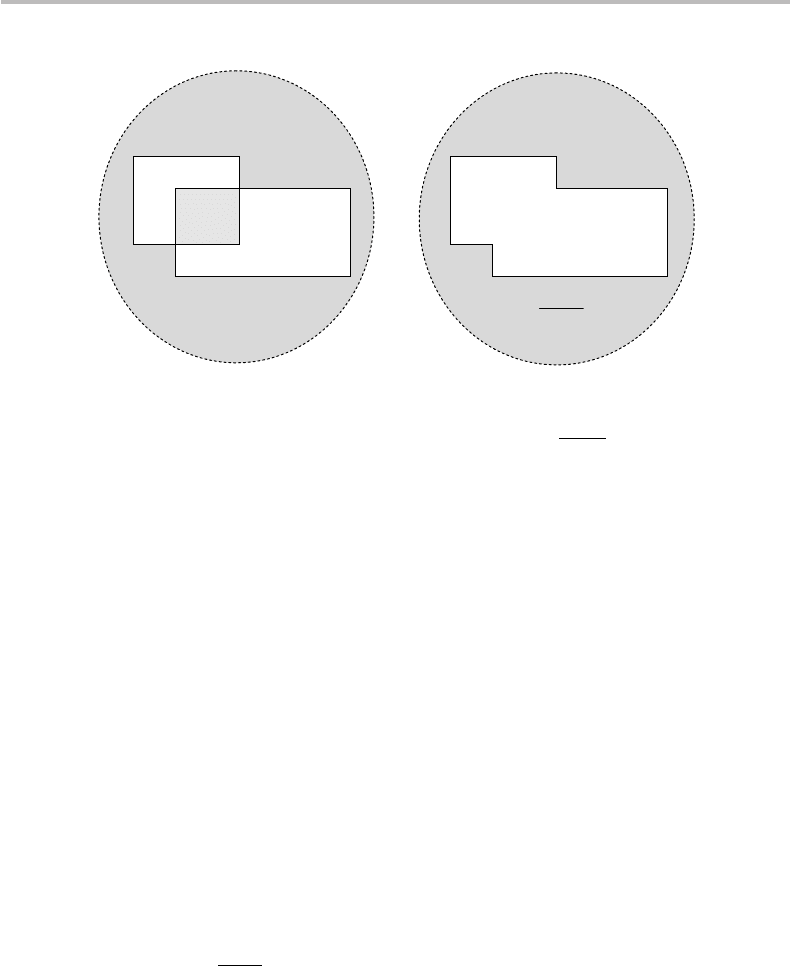
Figure 1.4 Venn diagrams showing event space S and its subspaces A and B, with: (a) the

intersection A ∩ B and (b) the union A ∪ B and its complement

A ∪ B.

A visual representation of these two deﬁnitions is provided by Venn diagrams, as illus-

trated in Fig. 1.4.

In the ﬁgure, the circle S represents the set of all possible occurrences. Its surface

is equal to unity. The rectangles A and B represent the set of occurrences for the two

events a, b, respectively, and their surfaces correspond to the associated probabilities.

The intersection of the two rectangles, A ∩ B, deﬁnes the number of occurrences (the

probability) for the joint event, a ∩ b. The union of the two rectangles, A ∪ B, deﬁnes

the number of occurrences (the probability) of the combined event, a ∪ b. If we note

n(x), the number of occurrences for the event x, then we have

n(a ∪ b) = n(a) +n(b) − n(a ∩ b). (1.11)

The term that is subtracted in the right-hand side in Eq. (1.11) corresponds to events

that would be otherwise counted twice.

Two events are said to be mutually exclusive if n(a ∩ b) = 0, meaning that the second

cannot be observed if the ﬁrst occurs, and the reverse. In this case, we have the property

n(a ∪ b) = n(a) +n(b).

As a third deﬁnition, the complementary event of x is the event that occurs if x does

not occur. It is noted

x or sometimes ¬x.InFig.1.4, the complementary event of a ∪ b,

which is noted

a ∪ b, is represented by the shaded surface spreading inside the space S

and outside the surface of a ∪ b.

Since any event probability p(x) is proportional to its number of occurrences, x,the

previous relation can also be written under the form:

p(a ∪ b) = p(a) + p(b) − p(a ∩ b), (1.12)

which is also usually written as

p(a + b) = p(a) + p(b) − p(a, b), (1.13)

1.3 Combined, joint, and conditional probabilities 13

where p(a ∪ b) ≡ p(a + b)isthecombined probability of the two events a, b and

p(a ∩ b) ≡ p(a, b) is the corresponding joint probability (one must be careful to read

the + sign in p(a + b) as meaning “or” and not “and”).

Finally, the probability p(

x) of the complementary event of x (x = a, b, a ∪ b,

a ∩ b..)isgivenby

x) = 1 − p(x). (1.14)

Let us apply now the above properties with two illustrative examples.

Taking exams

Two students, John and Peter, must take an exam. The probability that John passes is

p(John pass) = 0.7 and for Peter it is p(Peter pass) = 0.4. The probability that they both

pass is p(John pass ∩ Peter pass) = 0.3. What are the probabilities that:

(a) At least one of the two students passes the exam?

(b) The two students fail the exam?

Answer: In the event (a), we have

p(John pass ∪ Peter pass) = p(John pass) + p(Peter pass) − p(John pass ∩ Peter pass)

= 0.7 +0.4 −0.3 = 0.8.

The event (b) is the complement of event (a), since the two are mutually exclusive (at

least one passing excludes both failures). Therefore

p(John fail ∩ Peter fail) = 1 − p(John pass ∪Peter pass)

= 1 −0.8 = 0.2.

The probability of the event (c) can be calculated as follows:

p(John fail ∪ Peter fail) = p(John fail) + p(Peter fail) − p(John fail ∩Peter fail)

= (1 −0.7) +(1 −0.4) −0.2 = 0.7.

To conclude this example, we should take note of an interesting feature. Indeed, we

have

p(John pass) ∪ Peter pass = 0.3

> p(John pass) × p(Peter pass) = 0.7 ×0.3 = 0.21,

which means that the probability of both students passing the exam is greater than the

product of their respective probabilities of succeeding. This means that the events of their

individual successes are correlated. This notion of event correlation will be clariﬁed

further on.

14 Probability basics

Sharing birthdays

Given a group of people, the issue is to ﬁnd how many persons may share your birthday

(assuming that birth events are independent):

(a) In a group of n people, what is the probability of ﬁnding at least one person who

shares your birthday?

(b) How many people n should be in the group so that this probability is 50%?

persons sharing the same birthday is 50%?

Answer: The probability that any person met at random shares your birthday is 1/365

(since your birthday is one date out of 365 possibilities

), which is relatively small

(1/365 = 0.27%). The probability that this person does not share your birthday is thus

364/365 = 99.7%, which is relatively high, as expected.

To answer question (a), we consider the complementary event

x = nobody in this

group shares your birthday. The probability that two persons selected at random do

not share your birthday is (364/365)

, thus for a group of n people we have p(

x) =

(364/365)

. The probability that at least one person shares your birthday is, therefore,

p(x) = 1 − p(

x) = 1 − (364/365)

Question (b) is answered by ﬁnding the value of n for which p(x) ≈ 0.5. With

a pocket calculator, one easily ﬁnds after a few trials that n = 253 (or alternatively

by computing n = log(0.5)/ log(364/365)). As expected, this is a relatively large

group.

Question (c) leads to a nonintuitive result, as we shall see. The number of ways of

selecting a pair of persons in a group of n people is C

= n(n − 1)/2. The probability

that two people do not share birthdays is 364/365. Thus, the probability of ﬁnding no

matching pair in the whole group is p(

x) = (364/365)

n(n−1)/2

, and the probability of

ﬁnding at least one matching pair is p(x) = 1 − p(

x) = 1 − (364/365)

n(n−1)/2

. Solving

for p(x) ≈ 0.5(orn(n − 1)/2 = 253) yields n = 23. Thus, a group as small as 23 people

has a 50% chance of including at least two persons sharing the same birthday. Such a

result is indeed far from intuitive!

I address next the concept of conditional probabilities. By deﬁnition, the conditional

probability p(b

a)isthe probability that event b occurs given the fact that event a has

occurred. The factual knowledge regarding the ﬁrst event thus provides a clue regarding

the likelihood of the second.

The conditional probability is calculated according to what is called Bayes’s theorem:

p(b

a ) =

p(a, b)

p(a)

. (1.15)

For simplicity, we excluded here people born on February 29th (which only happens every four years). It is

also assumed that birthday events are independent, which is not true in real life, for instance, due to seasonal

peaks (i.e., observed peaks in the summer months) and effects of induced labor (i.e., a majority of births

happen on weekdays). A full analysis of the different ways to analyze and solve the Birthday paradox can

be found in http://en.wikipedia.org/wiki/Birthday

paradox.

1.3 Combined, joint, and conditional probabilities 15

Alternatively, we can write

p(a, b) = p(b

a )p(a) = p(a

b ) p(b), (1.16)

which deﬁnes the fundamental relation between joint and conditional probabilities.

If there is no correlation whatsoever between two events a and b, the events are said to

be uncorrelated or independent. This means that the probability of b knowing a (or any

other event different from b) is unchanged, which implies that p(b

a) ≡ p(b). Likewise,

the probability of a knowing b must also be unchanged, or p(a

b) ≡ p(a). Replacing

these two results in Eq. (1.16) yields a fundamental property for the joint probability of

independent/uncorrelated events:

p(a, b) = p(a)p(b). (1.17)

In the opposite case to correlated or dependent events, we have p(a, b) = p(a) p(b),

which means that either p(a, b) > p(a) p(b)or p(a, b) < p(a) p(b), representing two

possibilities (the second case is being referred to as anti-correlation).

Let us play with conditional probabilities through an illustrative example.

Party meetings

Assume that the probabilities of meeting two old friends, Alice and Bob, in a party are

p(Alice) = 0.6 and p(Bob) = 0.4, respectively. The probability of meeting Bob if we

know that Alice is there is p(Bob

Alice ) = 0.5. Then what are the probabilities of:

(a) Meeting at least one of them?

(b) Meeting both Alice and Bob?

Answer: For question (a), let’s apply the theorem in Eq. (1.13) combined with Bayes’s

theorem in Eq. (1.16) to get:

p(Alice + Bob) = p(Alice) + p(Bob) − p(Alice, Bob)

= p(Alice) + p(Bob) − p(Bob

Alice ) p(Alice).

= 0.6 +0.4 −0.5

∗

0.6 = 0.7

For question (b), we directly calculate the joint probabilities as follows:

p(Alice, Bob) = p(Bob

Alice ) p(Alice) = 0.5

∗

0.6 = 0.3.

For question (c), we apply Bayes’s theorem to get:

p(Alice

Bob ) =

p(Alice, Bob)

p(Bob)

0.3

0.4

= 0.75.

We see from the results that the most likely outcome is to meet at least one of them,

(p(Alice + Bob) = 0.7), meaning either Alice or Bob or both. The less likely outcome is

to meet both ( p(Alice, Bob) = 0.3). But if Alice is ﬁrst seen there, it is much more likely

to see Bob (p(Bob

Alice ) = 0.7 > p(Bob) = 0.4) and if Bob is ﬁrst seen there, it is a bit

more likely to see Alice ( p(Alice

Bob ) = 0.75 > p(Alice) = 0.6). These last two facts

16 Probability basics

illustrate the correlation between the respective presences of Alice and Bob. If their

presence were not correlated, we would have p(Alice, Bob) = p(Alice) × p(Bob) =

0.6

∗

0.4 = 0.24, which is a lower probability than found here ( p(Alice, Bob) = 0.3). This

shows that the known presence of either one increases the chances of seeing the other,

a fact that is usually veriﬁed in parties or social life! Incidentally, the probability that

neither Alice nor Bob be seen at the party is p(

Alice + Bob) = 1 − p(Alice + Bob) =

1 − 0.7 = 0.3. Thus, there exist equal chances of seeing them both or of seeing neither

of them, but this is only coincidental to this example.

I shall conclude this section and chapter by considering the probabilities associated

with a succession of independent or uncorrelated events. As we have seen, if x

, x

are independent events with probabilities p(x

), p(x

), their joint probability is simply

given by the product p(x

, x

) = p(x

) × p(x

). Thus for three independent events, we

have p(x

, x

) = p(x

, x

) × p(x

) = p(x

)p(x

), and so on.

Consider a few examples to illustrate the point.

Tossing the coin

What is the probability that a ﬂipped coin lands three times on the same side?

Answer: The probability of getting either three tails or three heads is q = (1/2)

= 0.125.

But there is a trick: since either succession of events is possible (i.e., getting three heads

or three tails), the total probability is actually 0.125 + 0.125 = 0.250 = 1/4.

Double six

Rolling two dice, what is the number of trials required to obtain a double six with a

chance of at least 50%?

Answer: The probability of getting a six from a single die is p(6) = 1/6. Since the two

dice are independent (their outcome is uncorrelated), the joint probability for a double

six is p(6, 6) = p(6) × p(6)(1/6)

= 1/36. The probability of not getting a double six

is therefore q = 1 − p(6, 6) = 1 −1/36 = 35/36 = 0.97222 ...The probability of not

getting a double six after N trials is q

. We must then ﬁnd the number N, such that q

≤

0.5, meaning that the complementary event (not getting any double six) has the proba-

bility 1 − q

≥ 0.5, or greater than 50%. Solving this equation for N is straightforward

using the successive steps: N log q = N log(35/36) ≤ 0.5, then −N log(36/35) ≤ 0.5,

then N ≥ 0.5/ log(36/35). The equation can also be solved using a computer spread-

sheet. Either method yields the solution N = 25, for which 1 − q

= 0.5055.

Drawing cards

Five cards are successively drawn at random from a 32-card deck. What are the

probabilities for the resulting hand to:

(a) Have only red cards?

(b) Include at least one ace?