Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

1.3 Combined, joint, and conditional probabilities 17

Answer: Recall ﬁrst that a 32-card deck has four series (red hearts, red diamonds, black

clubs, and black spades) of eight cards each, including an ace, a king, a queen, a jack

and four cards having the values 10, 9, 8, and 7.

Considering question (a), we must calculate the probability of drawing ﬁve red cards

successively. We ﬁrst observe that half of the cards (16) have the same (red or black)

color. The probability of drawing a red card is thus

,or,moreformally, p(x

red) = C

= 16/32 = 1/2. For the second draw, we have 31 cards left, which by

deﬁnition include only 15 red cards. Thus, p(x

= red) = C

= 15/31, and so on

for the other three selections. The ﬁnal answer for the joint probability is, therefore:

p(red, red, red, red, red) =

= 0.021.

Question (b) concerns a hand having at least one ace. We could go through all the

possibilities of successively drawing ﬁve cards with one, two, three, or four aces, but

we can proceed much more quickly. Indeed, we can instead calculate the probability of

the complementary event “no ace in hand,” then use the property p(at least one ace) =

1–p(no ace). The task is to use combinatorics to evaluate the probabilities of having

no ace at each draw. The number of ways of drawing a ﬁrst card that is not an ace

is C

32−4

= C

= 28. The probability of having no ace in the ﬁrst draw is, therefore,

28/32. With similar reasoning for the next four draws, it is straightforward to obtain

ﬁnally:

p(no ace) =

= 0.488,

and p(at least one ace) = 1 −0.488 = 0.511. We see that the probability of eventually

having at least one ace in the ﬁve-card hand is a little over 50%, which was not an

intuitive result. The lesson learnt is that successive events may be independent, but their

respective probabilities keep evolving according to the outcome of the preceding events.

Put otherwise, each occurring event affects the space of the next series of events, even

if all events are 100% independent.

To complete this ﬁrst chapter, I must introduce the summing rule of conditional

probabilities, also called the law of total probability. Assume two complete and disjoint

event spaces S ={a, b} and T ={x, y, z}, with S ∩ T =∅(the symbol ∅ meaning an

empty set or a set having zero elements) and with, by deﬁnition of probabilities p(a) +

p(b) = 1, and p(x) + p(y) + p(z) = 1. Then the following summing relations hold:



p(x) = p(x

a )p(a) + p(x

b ) p(b)

p(y) = p(y

a )p(a) + p(y

b ) p(b)

(1.18)

and



p(a) = p(a

x ) p(x) + p(a

y ) p(y) + p(a

z )p(z)

p(b) = p(b

x ) p(x) + p(b

y ) p(y) + p(b

z )p(z).

(1.19)

18 Probability basics

Thus with the knowledge of the conditional probabilities p(·

·) relating the two event

space causalities, one is able to compute the probabilities from one space to the other.

It is important to note that while the conditionalp(·

·)aretrueprobabilities, they do not

sum up to unity, a mistake to avoid by ﬁrmly memorizing any of the above summing

relations.

1.4 Exercises

1.1 (B): Flipping two coins simultaneously, what are the probabilities associated with

the following events:

(a) Getting two heads?

(b) Getting one heads and one tails?

1.2 (B): Rolling three dice, one wins if the outcome is 4, 2, 1 in any order. What is the

probability of winning in the ﬁrst, the second, and the third dice roll? What is the

number of rolls required to have at least a 50% chance of winning?

1.3 (B): A lotto game has 50 numbered balls, out of which six are picked at random.

What is the probability of winning by betting on any six-number combination?

1.4 (B): Three competing car companies, A, B, and C, have market shares of 60%, 30%,

and 10%, respectively. The probabilities that the cars will show some construction

defects are 5% for A, 7% for B, and 15% for C. What is the probability for any car

bought at random to show some construction defect?

1.5 (M): A bag contains ten billiard balls numbered from one to ten. If two balls are

picked at random from the bag, what is the probability of getting:

(a) Two balls with even numbers?

(b) At least one ball with an odd number?

You must propose two different methods of solving the exercise.

The summing rule can be generalized, assuming X ={x

, x

,...x

} and Y ={y

, y

,...y

}, into the

following:

p(y

) = p(y

)p(x

) + p(y

)p(x

) +···p(y

)p(x

) =



j=1

p(y

)p(x

which can also be expressed as a matrix–vector relation, P

with P

={p(x

),..., p(x

)} and

={p(y

),..., p(y

)} being column vectors, and U the M × N “conditional” or “transition” matrix:

U =







(

)

(

)

··· p

(

)

(

)

··· ···

. ··· ···

(

)

··· ··· p

(

)







1.4 Exercises 19

1.6 (M): The American roulette has 36 spots numbered 1, 2,...,36, which are alterna-

tively divided into 18 red spots (odd numbers) and 18 black spots (even numbers),

plus two green spots, called 0 and 00. The roulette’s outcome is any single number.

It is possible to bet on any number (single or combination), or on red, black, odd,

even, the ﬁrst 12 (numbers 1–12), the second 12 (numbers 13–24), and the third 12

(numbers 25–36). The roulette payoffs are 35 to 1 for a winning number, 2 to 1 for

a winning red/black/even/odd number and 3 to 1 for a winning ﬁrst/second/third

12 number. What are the odds of winning any of these bets? Comments? What

is the probability of winning at least once after playing single numbers 36 times

successively?

1.7 (T): In the lotto game of Exercise 1.3, what are the probabilities of having either

exactly one or exactly two winning numbers in the six-number combination?

1.8 (T): This is a television game show where the contestant may win a car. The car

is standing behind one of three doors. The payer ﬁrst designates one of the three

doors. The host then opens another door, which reveals . . . a goat! Then the host

asks the contestant: “Do you maintain your choice?” The question here is: what is

in the contestant’s interest? To maintain or to switch his or her choice? Clue: The

answer is not intuitive!

2 Probability distributions

Chapter 1 enabled us to familiarize ourselves (say to revisit, or to brush up?) the concept

of probability. As we have seen, any probability is associated with a given event x

from

a given event space S ={x

, x

,...,x

}. The discrete set {p(x

), p(x

),..., p(x

)}

represents the probability distribution function or PDF, which will be the focus of this

second chapter.

So far, we have considered single events that can be numbered. These are called

discrete events, which correspond to event spaces having a ﬁnite size N (no matter

how big N may be!). At this stage, we are ready to expand our perspective in order

to consider event spaces having unbounded or inﬁnite sizes (N →∞). In this case,

we can still allocate an integer number to each discrete event, while the PDF, p(x

remains a function of the discrete variable x

. But we can conceive as well that the event

corresponds to a real number, for instance, in the physical measurement of a quantity,

such as length, angle, speed, or mass. This is another inﬁnity of events that can be

tagged by a real number x. In this case, the PDF, p(x), is a function of the continuous

variable x.

This chapter is an opportunity to look at the properties of both discrete and continuous

PDFs, as well as to acquire a wealth of new conceptual tools!

2.1 Mean and variance

In this section, I shall introduce the notions of mean and variance. I will consider ﬁrst

discrete then continuous PDFs, with illustrative examples from the physical world. I

will then show that in the limit of a large number of events, the discrete case can be

approximated by the continuous case (the so-called asymptotic limit).

Consider then the discrete case, as deﬁned by the sample/event space S =

, x

,...,x

}, where N can be inﬁnite (notation being N →∞). The associated

PDF is called p(x), which is a function of the random variable x, which takes the

discrete values x

(i = 1,...,N ). When writing p(x

), this conceptually means “the

probability that event x takes the value x

.” The mean, which is noted <x>,oralso

or E(x), is given by the weighted sum

<x> =



i=1

p(x

). (2.1)

2.1 Mean and variance 21

The mean represents what is also called the expectation value, hence the notation E (x).

Contrary to what the word “expectation” would suggest, E(x) is not the value one should

expect for the outcome of event x after some sufﬁcient number of trials. Rather, it is the

mean value of x that one should expect to become, independent of the number of trials

N , as this number indeﬁnitely increases, and assuming that the PDF is constant over

time.

As an illustration, take the event space S ={1, 2, 3, 4, 5, 6} corresponding to the

outcomes of rolling a single die. As we know, the PDF is p(x) = 1/6 for all events x.

The mean value is, therefore,

<x> =



i=1

p(x

) =



i=1

(1 + 2 +3 +4 +5 +6) = 3.5. (2.2)

This example illustrates what should be understood by “expected value.” In no way would

a die fall on x = 3.5, and nobody would “expect” such a result! The number simply

represents the average count of spots, were we to perform an inﬁnite (say, sufﬁciently

large) number of die rolls. Looking back at Fig. 1.2 (counting spots from two dice), we

observe that the PDF is centered about x = 7, which represents the mean value of all

possibilities. The mean value should, therefore, not be interpreted as representing the

event of highest probability, i.e., where the PDF exhibits a peak value, although this

might be true in several cases, like the PDF in Fig. 1.2.

But the mean does not tell the whole story about a PDF. I introduce a second parameter

called PDF variance. The variance, typically noted σ

, is deﬁned as the expected value

(

x − <x>

)

. Thus, using basic algebra:

= <(x − <x>)

= <x

− 2x<x> + <x>

= <x

> − 2<x><x> + << x>

> (2.3)

= <x

> − 2<x>

+ <x>

= <x

> − <x>

(noting that << x>

> = <x>

, since <x>

is a number, not a variable). The variance

is the difference between the expected value of x

and the square of the mean. It is always

a positive number. We can thus take its square root, which is called the PDF standard

deviation:

σ =

√

≡



> − <x>

. (2.4)

How does one calculate the mean square <x

>? Consistent with the earlier deﬁnition

in Eq. (2.1), we have

> =



i=1

p(x

). (2.5)

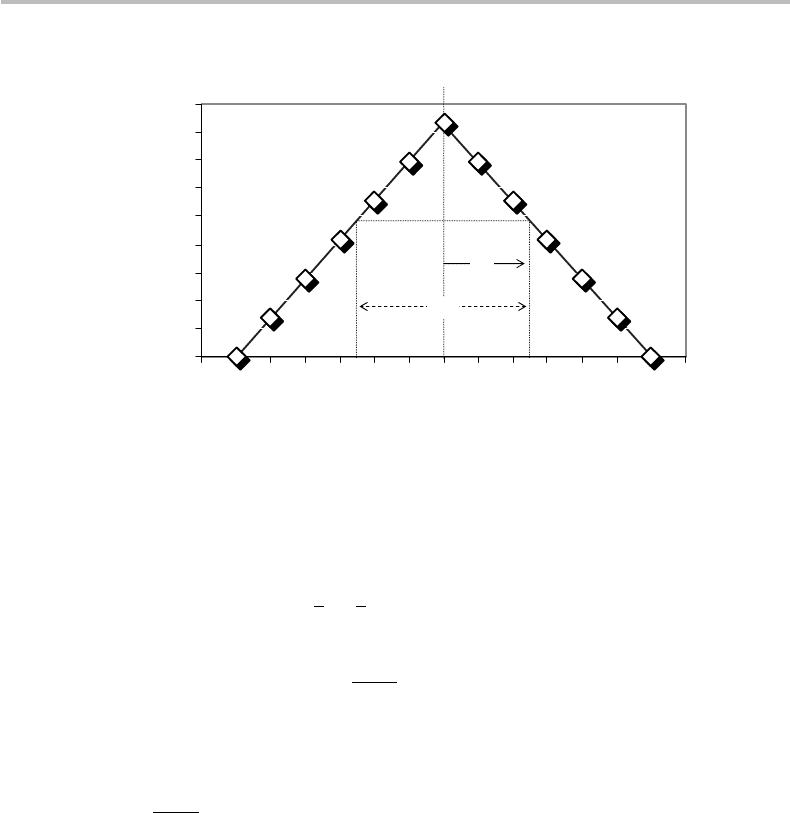
22 Probability distributions

0.000

0.020

0.040

0.060

0.080

0.100

0.120

0.140

0.160

0.180

01234567891011121314

Count

Probability

Figure 2.1 Same probability distribution function (PDF) as in Fig. 1.2(b), illustrating the

concepts of mean (<x> = 7) and standard deviation (σ = 2.415).

As an illustration, let us then calculate the standard deviations of the one-die and two-dice

PDF. In the one-die case, we have

> =



i=1

+ 2

+ 3

+ 4

+ 5

+ 6

) = 15.166. (2.6)

The one-die PDF variance is, thus, σ

= <x

> − <x>

= 15.166 −3.5

= 2.916, and

the standard deviation is σ =

√

2.916 = 1.707.

We can get a better sense of the meaning of such a “deviation” with the two-dice

example. It takes a computer spreadsheet (or pocket-calculator patience) to com-

pute <x

> with the PDF shown in Fig. 1.2(b), but the reader will easily check that

the result is <x

> = 54.833, hence σ

= <x

> − <x>

= 54.833 −7

= 5.833, and

σ =

√

5.833 = 2.415.

Reproducing, for convenience, the same PDF plot in Fig. 2.1, we see that the interval

[

<x> − σ, <x> + σ

]

≈

[

4.5, 9.5

]

, of width 2σ , deﬁnes the PDF region where the

probabilities are the highest, i.e., about greater or equal to half the peak value. In other

words, the outcome of the two-dice roll is most highly likely to fall within the 2σ

region.

Statistics experts familiarly state that the event to be expected is <x> with a ±σ

accuracy or trust interval. However, such a conclusion does not apply with other types

of PDF, for instance, with the uniform distribution, as I will show further below.

2.2 Exponential, Poisson, and binomial distributions

I shall now consider three basic examples of discrete PDFs. As we shall see, these

PDFs govern many physical phenomena and even human society! They are the

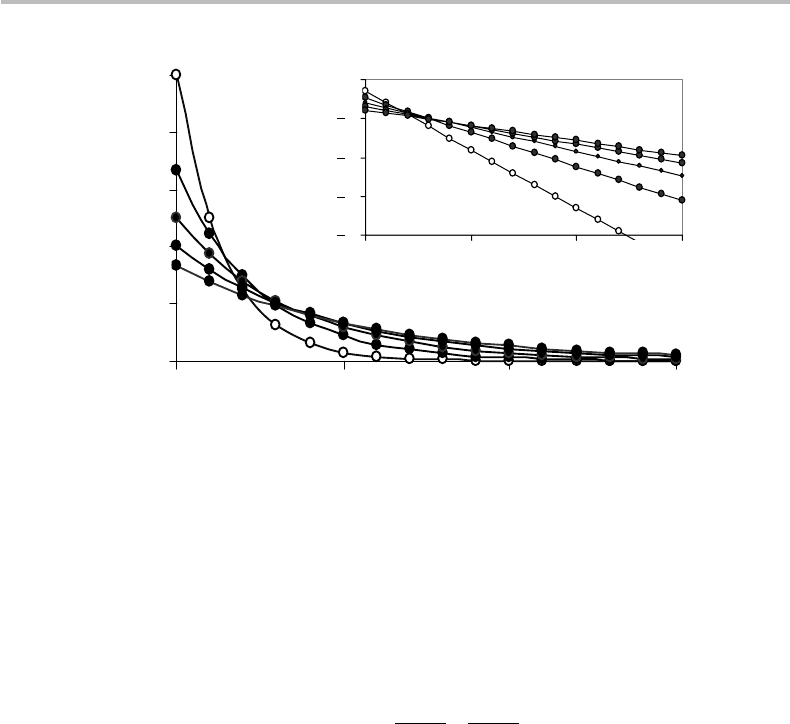
2.2 Exponential, Poisson, and binomial distributions 23

0.1

0.2

0.3

0.4

0.5

0 5 10 15

(

)

0 5 10 15

Log[

(

)]

Figure 2.2 Plots of discrete-exponential or Bose–Einstein probability distribution corresponding

to mean values <n> = N = 1, 2, 3, 4, 5 (open symbols corresponding to the case <n> = 1).

The inset shows the same plots in decimal logarithmic scale.

discrete-exponential distribution, the Poisson distribution, and the binomial distribu-

tion. To recall that these three PDFs concern discrete random variables, I will use the

notations <n> and p(n), instead of <x> and p(x), which we reserve for continuous

distributions.

The discrete-exponential distribution,alsoreferredtoastheBose–Einstein (BE)

distribution, is deﬁned according to

p(n) =

N + 1



N + 1



, (2.7)

where <n> = N is the mean value. This PDF variance is simply σ

= N + N

Figure 2.2 shows plots of the exponential distribution for various values of N , in both

linear and logarithmic scales. The continuous lines linking the data are only shown to

guide the eye, recalling that the PDF applies to the discrete variable n. The PDF is seen to

be linear in the logarithmic plot, which allows a better visualization of the evanescent tail

at high n. As the ﬁgure also illustrates, the peak value of the exponential/BE distribution

is reached at the origin n = 0, with p(0) = 1/(N + 1).

In the physics world, such a distribution is representative of thermal processes. Such

processes concern, for instance, the emission of photons (the electromagnetic energy

quanta) by hot sources, such as an incandescent light bulb or a star, like the sun, or the

distribution of electrons in atomic energy levels, and many other physical phenomena.

As we shall see in the forthcoming chapters, the discrete-exponential distribution is

important in information theory. We will also see that the exponential PDF is commonly

found in human society, for instance, concerning the distribution of alphabetic characters

in Western languages.

Let us consider next another PDF of interest, which is the Poisson distribution.This

PDF is used to predict the number of occurrences of a discrete event over a ﬁxed

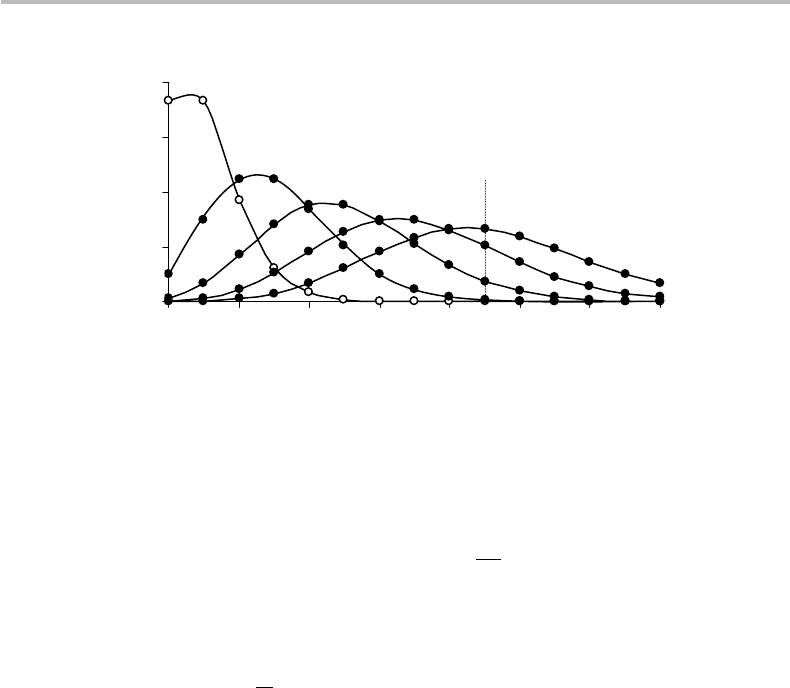
24 Probability distributions

0.1

0.2

0.3

0.4

02468101214

(

)

= 9

Figure 2.3 Plots of the Poisson distribution corresponding to mean values

<n> = N = 1, 3, 5, 7, 9 (open symbols corresponding to the case <n> = 1).

time interval. If N is the expected number of occurrences over that time interval, the

probability that the count is exactly n is

p(n) = e

−N

. (2.8)

As a key property, the Poisson PDF variance is equal to the PDF mean, i.e., σ

= N .

Figure 2.3 shows plots of the Poisson PDF for various values of the mean N .

It is seen from the ﬁgure that as N increases, the distribution widens (but slowly,

according to σ =

√

N ). Also, the line joining the discrete points progressively takes the

shape of a symmetric bell curve centered about the mean, as illustrated for N = 9(the

mean coinciding with the PDF peak only for N →∞). This property will be discussed

further on, when considering continuous distributions.

There exist numerous examples in the physical world of the Poisson distribution,

referred to as Poisson processes. In atomic physics, for instance, the Poisson PDF

deﬁnes the count of nuclei decaying by radioactivity over a period t. Given the decay

rate λ (number of decays per second), the mean count is N = λt, and the Poisson PDF

p(n) gives the probability of counting n decays over that period. In laser physics, the

Poisson PDF corresponds to the count of photons emitted by a coherent light source, or

laser. Poisson processes are also found at macroscopic and human scales: for instance,

the number of cars passing under a highway bridge over a single lane, the number of

phone calls handled by a central ofﬁce, the number of Internet hits received by a website,

the number of bonds traded in the stock exchange, or the number of raindrops falling on

a roof window. Each of these counts, being made within a given amount of time, from

seconds to minutes to hours to days, obeys Poisson statistics.

The binomial distribution, also called the Bernoulli distribution, describes the number

of successes recorded in a discrete sequence of independent trials. Here, let’s call k the

random variable, which is the number of successes, and n the ﬁxed number of trials,

with k ≤ n. If the probability of success for a single independent trial is q, the binomial

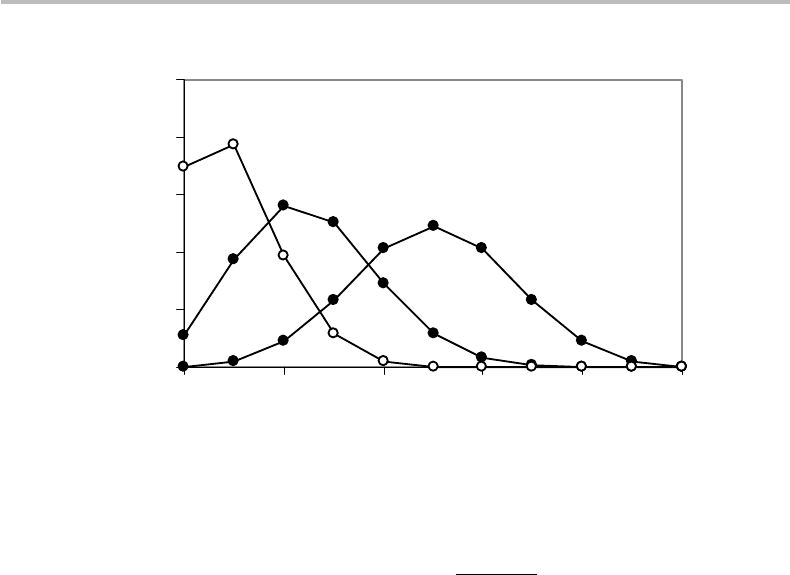
2.2 Exponential, Poisson, and binomial distributions 25

0.1

0.2

0.3

0.4

0.5

02 46810

(

)

Figure 2.4 Plots of the binomial or Bernoulli distribution corresponding to parameters

q = 0.1, 0.25, 0.5 with n = 10 mean (open symbols corresponding to the case q = 0.1).

PDF is deﬁned according to:

p(k) = C

(1 − q)

n−k

≡

k!(n − k)!

(1 − q)

n−k

. (2.9)

Such a deﬁnition makes sense, considering that the probability of obtaining k indepen-

dent successes is q

and the probability of failure for the remaining n − k events is

(1 − q)

n−k

. The product of the two is the joint probability of the group of measurements,

as observed in any speciﬁc order. The combinatorial factor C

is the number of possible

orders for successive success or failure measurements. The mean and variance of the

binomial distribution is N = nq and σ

= N (1 −q), respectively. Figure 2.4 shows

plots of the binomial PDF for n = 10 and different values of q. We observe that the PDF

is asymmetric except when q = 0.5, in which case the peak value is exactly centered

about N .

A physical illustration of the Bernoulli distribution is the passing, one at a time, of a

stream of individual particles (like light quanta or photons) through a piece of absorbing

material. These particles may either successfully pass through the material (success,

probability q), or absorbed by it (failure, probability 1 −q). Assuming an ideal particle

counter, the probability of counting k particles after the stream has passed though the

material is effectivelyp(k), as deﬁned by Eq. (2.9). See also Section 2.5 in the bean

machine example.

We note that the binomial distribution is deﬁned over the ﬁnite random-variable

interval 0 ≤ k ≤ n. Since there is no restriction on the size of the sampling space deﬁned

by n, the PDF can be extended to the limit n →∞. It can be shown that in this inﬁnite

limit, the binomial PDF is equal to the Poisson PDF previously described. It can also be

shown that, for large mean numbers N , the Poisson (or binomial) PDF asymptotically

converges towards the Gaussian or normal distribution, which is described in the next

section.

26 Probability distributions

2.3 Continuous distributions

At the beginning of this chapter, I discussed the possibility that the events form a con-

tinuous and inﬁnite suite of real numbers, which, in the physical world, represent the

unbounded set of measurements of a physical quantity. The likelihood of the measure-

ment then corresponds mathematically to a continuous probability distribution. Like

discrete PDF, a continuous PDF p(x) must satisfy the property

0 ≤ p(x) ≤ 1 (2.10)

for all values x belonging to the event space x

min

, x

max

 within which the events

are deﬁned. By deﬁnition, the sum of all probabilities must be equal to unity. With a

continuous variable, such a sum is an integral, i.e.,



x=x

max

x=x

min

p(x)dx = 1. (2.11)

Consistent with the above deﬁnition, the PDF mean or expected value <x> and the

mean square are deﬁned as follows:

<x> =



x=x

max

x=x

min

xp(x)dx (2.12)

> =



x=x

max

x=x

min

p(x)dx, (2.13)

with the variance being σ

= <x

> − <x>

, just as in the discrete-PDF case. Note

that for any continuous PDF one can replace the interval

[

min

, x

max

]

[

−∞, +∞

]

with the convention that p(x) = 0forx /∈

[

min

, x

max

]

2.4 Uniform, exponential, and Gaussian (normal) distributions

In the following, we shall consider three basic types of continuous distribution: uniform,

exponential, and Gaussian (normal).

The most elementary type of continuous PDF is the uniform distribution.Itgivesa

good pretext to open up our integral-calculus toolbox. Such a distribution is deﬁned as

p(x) = const. over a certain interval

[

min

, x

max

]

and p(x) = 0 elsewhere. The constant

is found by applying Eq. (2.11), i.e.,



x=x

max

x=x

min

p(x)dx = const.



x=x

max

x=x

min

dx = const.(x

max

− x

min

) ≡ const.x = 1,

(2.14)

where x = x

max

− x

min

is the sample-space width, which gives const. = 1/x.

Figure 2.5 shows a plot of the uniform distribution thus deﬁned. The ﬁgure also illus-

trates that the PDF is actually deﬁned over the inﬁnite space

[

−∞, +∞

]

, while being