Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.

5.2 Mutual information 77
H
(
X
)
H
(
Y
)
H
(
X
;
Y
)
H
(
X
,
Y
)
H
(
X
;
Y Z
)
H
(
X
,
Y
,
Z
)
H
(
Z
)
H
(
X
;
Y
;
Z
)
H
(
XY
)
H
(
XY
,
Z
)
H
(
X
)
H
(
Y
)
H
(
Y X
)
H
(
Z X
,
Y
)
H
(
Y X
,
Z
)
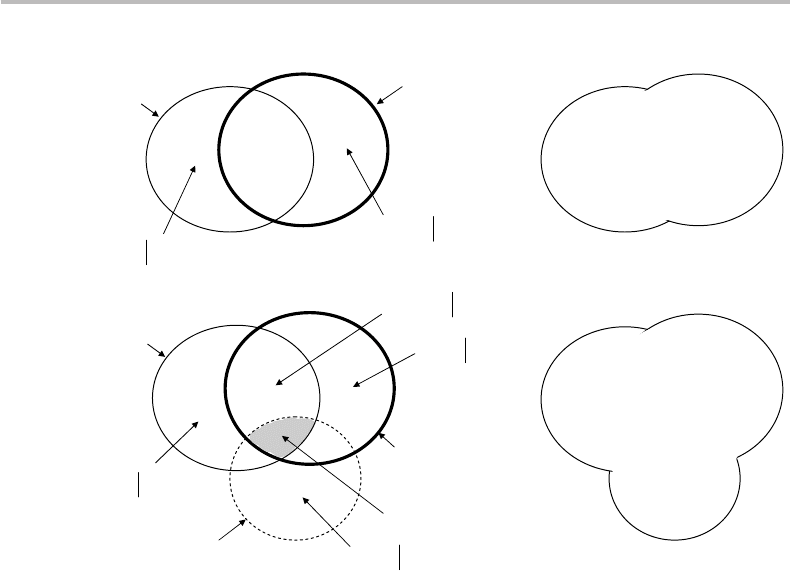
Figure 5.2 Venn diagram representation of entropy H (U), joint entropy H (U, V ), conditional
entropy H (U |V ), and mutual information H (U; V ), for two (U = X, Y )orthree
(U, V = X, Y, Z ) sources.
that the following equivalences hold:
H(X, Y ) ↔ H (X ∪ Y )
H(X ; Y ) ↔ H (X ∩ Y )
H(X |Y ) ↔ H (X ∩¬Y )
H(Y |X ) ↔ H (Y ∩¬X).
(5.15)
The first equivalence in Eq. (5.15) means that the joint entropy of two sources is the
entropy of the source defined by their combined events.
The second equivalence in Eq. (5.15) means that the mutual information of two
sources is the entropy of the source containing the events they have in common.
The last two equivalences in Eq. (5.15) provide the definition of the conditional
entropy of a source U given the information on a source V . The conditional entropy is
given by the contributions of all the events belonging to U but not to V . This property
is far from obvious, unless we can visualize it. Figure 5.2 illustrates all the above logical
equivalences through Venn diagrams, using up to three sources.
Considering the two-source case, we can immediately visualize from Fig. 5.2 to which
subsets the differences H(X) − H (X; Y ) and H (Y ) − H (X ; Y ) actually correspond.
Given the identities listed in Eq. (5.15), we can call these two subsets H (X|Y ) and
H(Y |X ), respectively, which proves the previous point. We also observe from the Venn

78 Mutual information and more entropies
diagram that H(X |Y ) ≤ H (X ) and H (Y |X) ≤ H (Y ), with equality if the sources are
independent.
The above property can be summarized by the statement according to which condi-
tioning reduces entropy. A formal demonstration, using the concept of “relative entropy,”
is provided later.
The three-source case, as illustrated in Fig. 5.2, is somewhat more tricky because it
generates more complex entropy definitions with three arguments X, Y , and Z . Con-
ceptually, defining joint or conditional entropies and mutual information with three (or
more) sources is not this difficult. Considering the joint probability p(x, y, z)forthe
three sources, we can indeed generalize the previous two-source definitions according
to the following:
H(X, Y, Z ) =−
x∈X
y∈Y
z∈Z
p(x, y, z)logp(x, y, z), (5.16)
H(X ; Y ; Z) =+
x∈X
y∈Y
z∈Z
p(x, y, z)log
p(x, y, z)
p(x)p(y) p(z)
, (5.17)
H(Z |X, Y ) =−
x∈X
y∈Y
z∈Z
p(x, y, z)logp(z|x, y), (5.18)
H(X, Y |Z ) =−
x∈X
y∈Y
z∈Z
p(x, y, z)logp(x, y|z). (5.19)
These four definitions correspond to the joint entropy of the three sources X, Y, Z (Eq.
(5.16)), the mutual information of the three sources X, Y, Z (Eq. (5.17)), the entropy of
source Z given the known entropy of X, Y (Eq. (5.18)), and the joint entropy of X, Y
given the known entropy of Z (Eq. (5.19)). The last two definitions are seen to involve
conditional probabilities of higher orders, namely, p(z|x, y) and p(x, y|z), which are
easily determined from the generalization of Bayes’s theorem.
5
Other entropies of the
type H (X; Y |Z) and H (X|Y ; Z ) are more tricky to determine from the above definitions.
But we can resort in all confidence to the equivalence relations and the corresponding
two-source or three-source Venn diagrams shown in Fig. 5.2. Indeed, a straightforward
observation of the diagrams leads to the following correspondences:
H(X ; Y |Z ) = H (X; Y ) − H (Z), (5.20)
H(X |Y ; Z) = H (X) − H (Y ; Z). (5.21)
Finally, the Venn diagrams (with the help of Eq. (5.15) make it possible to establish the
following properties for H (X, Y |Z ) and H (X|Y, Z). The first chain rule is
H(X, Y |Z ) = H (X|Z ) + H (Y |X, Z), (5.22)
5
As we have
p(x, y, z) = p(z|x, y) p(x) p(y) → p(z|x, y) ≡ p(x, y, z)/[ p(x) p(y)]
and p(x, y, z) = p(x, y|z) p(z) → p(x, y|z) =≡ p(x, y, z)/ p(z).

5.3 Relative entropy 79
which is easy to memorize if a condition |z is applied to both sides of the definition of
joint entropy, H (X, Y ) = H (X ) + H (Y |X ). The second chain rule,
H(X, Y |Z ) = H (Y |Z) + H(X |Y, Z ), (5.23)
comes from the permutation in Eq. (5.22) of the sources X, Y , since the joint entropy
H(X, Y ) is symmetrical with respect to the arguments.
The lesson learnt from using Venn diagrams is that there is, in fact, little to
memorize, as long as we are allowed to make drawings! The only general rule to
remember is:
H(U|Z ) is equal to the entropy H(U) defined by the source U (for instance, U = X, Y or
U = X; Y ) minus the entropy H(Z ) defined by the source Z , the reverse being true for H(Z |U).
But the use of Venn diagrams require us not to forget the unique correspondence between the
ensemble or Boolean operators (∪∩¬) and the separators (, ; |) in the entropy-function arguments.
5.3 Relative entropy
In this section, I introduce the notion of distance between two event sources and the
associated concept of relative entropy.
The mathematical concept of distance between two real variables x, y is famil-
iarly known as the quantity d =|x − y|. For two points A, B in the plane, with
coordinates (x
A
, y
A
) and (x
B
, y
B
), respectively, the distance is defined as d =
(x
A
− x
B
)
2
+ (y
A
− y
B
)
2
.
More generally, any definition of distance d(X, Y ) between two entities X, Y must
obey four axiomatic principles:
(a) Positivity, d(X, Y ) ≥ 0;
(b) Symmetry, d(X, Y ) = d(Y, X);
(c) Nullity for self, d(X, X) = 0;
(d) Triangle inequality, d(X, Z) ≤ d(Y, X) + d(Y, Z).
Consider now the quantity D(X, Y ), which we define as
D(X, Y ) = H (X, Y ) − H (X ; Y ). (5.24)
From the visual reference of the Venn diagrams in Fig. 5.2 (top), it is readily verified
that D(X, Y ) satisfies at least the first three above distance axioms (a), (b), and (c). The
last axiom, (d), or the triangle inequality, can also be proven through the Venn diagrams
when considering three ensembles X, Y, Z , which I leave here as an exercise. Therefore,
D(X, Y ) represents a distance between the two sources X, Y .
It is straightforward to visualize from the Venn diagrams in Fig. 5.2 (top) that
D(X, Y ) = H (X|Y ) + H (Y |X), (5.25)
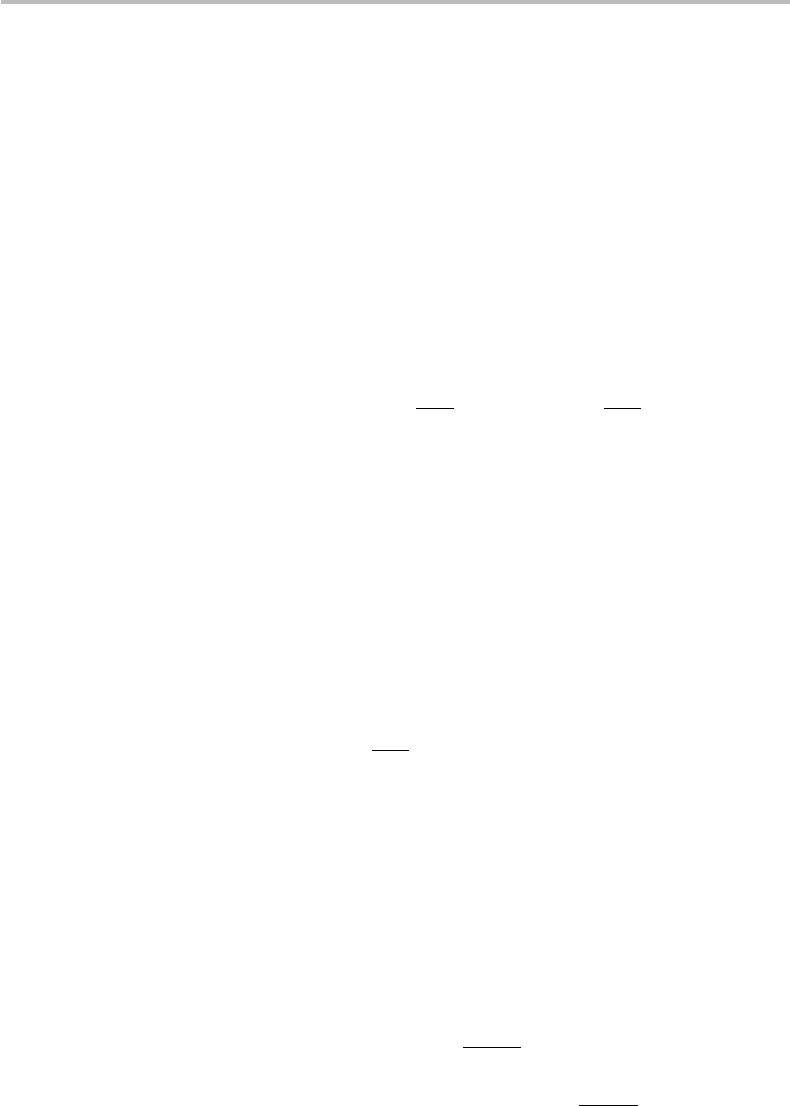
80 Mutual information and more entropies
or using the definition for the conditional entropies, Eq. (5.6), and grouping them
together,
D(X, Y ) =−
x∈X
y∈Y
p(x, y)log[p(x|y) p(y|x)]. (5.26)
We note from the above definition of distance that the weighted sum involves the joint
distribution p(x, y).
The concept of distance can now be further refined. I shall introduce the relative
entropy between two PDFs, which is also called the Kullback–Leibler (KL) distance or
the discrimination. Consider two PDFs, p(x) and q(x), where the argument x belongs
to a single source X.Therelative entropy,orKL distance, is noted D[ p(x)||q(x)] and
is defined as follows:
D[ p(x)q(x)] =
log
p(x)
q(x)
!
p
=
x∈X
p(x)log
p(x)
q(x)
. (5.27)
In this definition, the continuity limit ε log(ε) ≡ 0(ε → 0) applies, while, by convention,
we must set ε log(ε/ε
) ≡ 0(ε, ε
→ 0).
The relative entropy is not strictly a distance, since it is generally not symmetric
(D( pq) =D(qp), as the averaging is based on the PDF p or q in the first argument)
and, furthermore, it does not satisfy the triangle inequality. It is, however, zero for
p = q (D(qq) = 0), and it can be verified as an exercise that it is always nonnegative
(D[ pq] ≥ 0).
An important case of relative entropy is where q(x)isauniform distribution.Ifthe
source X has N events, the uniform PDF is thus defined as q(x) ≡ 1/N . Replacing this
definition in Eq. (5.27) yields:
D[ p(x)q(x)] =
x∈X
p(x)log
p(x)
1/N
= log N
x∈X
p(x) +
x∈X
p(x)logp(x) (5.28)
≡ log N − H (X ).
Since the distance D( pq) is always nonnegative, it follows from the above that H(X ) ≤
log N. This result shows that the entropy of a source X with N elements has log N for
its upper bound, which (in the absence of any other constraint) represents the entropy
maximum. This is consistent with the conclusion reached earlier in Chapter 4, where I
addressed the issue of maximizing entropy for discrete sources.
Assume next that p and q are joint distributions of two variables x, y. Similarly to
the definition in Eq. (5.27), the relative entropy between the two joint distributions is:
D[ p(x, y)q(x, y)] =
log
p(x, y)
q(x, y)
!
p
=
x∈X
y∈Y
p(x, y)log
p(x, y)
q(x, y)
. (5.29)
We note that the expectation value is computed over the distribution p(x, y), and,
therefore, D[p(x, y)q(x, y)] = D[q(x, y)p(x, y)] in the general case.

5.3 Relative entropy 81
The relative entropy is also related to the mutual information. Indeed, recalling the
definition of mutual information, Eq. (2.37), we get
H(X ; Y ) =
x∈X
y∈Y
p(x, y)log
p(x, y)
p(x)p(y)
≡ D[ p(x, y)p(x)p(y)], (5.30)
which shows that the mutual information between two sources X, Y is the relative
entropy (or KL distance) between the joint distribution p(x, y) and the distribution
product p(x)p(y). Since the relative entropy (or KL distance) is always nonnegative
(D(..) ≥ 0), it follows that mutual information is always nonnegative (H (X; Y ) ≥ 0).
This is consistent with results obtained in Section 5.2. Indeed, recalling the chain
rules in Eq. (5.13) and combining them with the property of nonnegativity (obtained in
section herein) yields:
H(X ; Y ) = H (X ) − H (X |Y ) = H (Y ) − H (Y |X) ≥ 0, (5.31)
which thus implies the two inequalities
H(X |Y ) ≤ H (X )
H(Y |X ) ≤ H (Y ).
(5.32)
The above result can be summarized under the fundamental conclusion, which has
already been established: conditioning reduces entropy.
Thus, given two sources X, Y , the information we obtain from source X given the
prior knowledge of the information from Y is less than or equal to that available from
X alone, meaning that entropy has been reduced by the fact of conditioning. The strict
inequality applies in the case where the two sources have nonzero mutual information
(H (X; Y ) > 0). If the two sources are disjoint, or made of independent events, then the
equality applies, and conditioning from Y has no effect on the information of X .
Next, I shall introduce another definition, which is that of conditional relative entropy,
given the joint distributions p and q over the space
{
X, Y
}
:
D[ p(y|x)q(y|x)] =
log
p(y|x)
q(y|x)
!
p
=
x∈X
y∈Y
p(x, y)log
p(y|x)
q(y|x)
, (5.33)
noting that averaging is made through the joint distribution, p(x, y). This definition is
similar to that of the relative entropy for joint distributions, Eq. (5.29), except that it
applies here to conditional joint distributions.
From Eqs. (5.27), (5.29), and (5.33), we can derive the following relation, or chain
rule, between the relative entropies of two single-variate distributions p(x), q(x) and
their two-variate or joint distributions p(x, y), q(x, y):
D[ p(x, y)q(x, y)] = D[ p(x)q(x)] + D[ p(y|x)q(y|x)]. (5.34)

82 Mutual information and more entropies
This chain rule can be memorized if one decomposes p(x, y) and q(x, y) through Bayes’s
theorem, i.e., p(x, y) = p(y|x) p(x) and q(x, y) = q(y|x)q(x), and rearranges the four
factors into two distance terms D
[
∗∗
]
. A similar chain rule thus also applies with x
and y being switched in the right-hand side.
The usefulness of relative entropy and conditional-relative entropy can only be appre-
ciated at a more advanced IT level, which is beyond the scope of these chapters. To satisfy
a demanding student’s curiosity, however, an illustrative example concerning the second
law of thermodynamics is provided. For this, one needs to model the time evolution of
probability distributions, which involves Markov chains. The concept of Markov chains
and its application to the second law of thermodynamics are described in Appendix D,
which is to be regarded as a tractable, bur somewhat advanced topic.
5.4 Exercises
5.1 (B): Given all possible events a ∈ A, and the conditional probability p(a|b)for
any event b ∈ B, demonstrate the summation property:
a∈A
p(a|b) = 1.
5.2 (M): If two sources X, Y represent independent events, then prove that
(a) H(X, Y ) = H (X) + H (Y ),
(b) H(X |Y ) = H (X ) and H (Y |X) = H (Y ).
5.3 (M): Prove the entropy chain rules, which apply to the most general case:
H(X, Y ) = H (Y |X) + H (X)
H(X, Y ) = H (X|Y ) + H (Y ).
5.4 (M): Prove that for any single-event source X, H (X|X ) = 0.
5.5 (M): Prove that for any single-event source X, H (X; X) = H (X).
5.6 (M): Establish the following three equivalent properties for mutual information:
H(X ; Y ) = H (X) − H (X |Y )
= H (Y ) − H (Y |X)
= H (X) + H(Y ) − H(X, Y ).
5.7 (M): Two sources, A =
{
a
1
, a
2
}
and B =
{
b
1
, b
2
}
, have a joint probability distri-
bution defined as follows:
p(a
1
, b
1
) = 0.3, p(a
1
, b
2
) = 0.4,
p(a
2
, b
1
) = 0.1, p(a
2
, b
2
) = 0.2.
Calculate the joint entropy H (A, B), the conditional entropy H(A|B) and
H(B|A), and the mutual information H (A; B).

5.4 Exercises 83
5.8 (B): Show that D(X, Y ), as defined by
D(X, Y ) = H (X, Y ) − H (X ; Y ),
can also be expressed as:
D(X, Y ) = H (X|Y )H(Y |X).
5.9 (T): With the use of the Venn diagrams, prove that
D(X, Y ) = H (X, Y ) − H (X ; Y )
satisfies the triangle inequality,
d(X, Z ) ≤ d(Y, X) +d(Y, Z ),
for any sources X, Y, Z.
5.10 (M): Prove that the Kullback–Leibler distance between two PDFs, p and q,is
always nonnegative, or D[pq] ≥ 0. Clue: assume that f = p/q satisfies Jensen’s
inequality,
f (u)≤f (u).

6 Differential entropy
So far, we have assumed that the source of random symbols or events, X,isdiscrete,
meaning that the source is made of a set (finite or infinite) of discrete elements, x
i
.To
such a discrete source is associated a PDF of discrete variable, p(x = x
i
), which I have
called p(x), for convenience. In Chapter 4, I have defined the source’s entropy according
to Shannon as H(X) =−
i
p(x
i
)logp(x
i
), and described several other entropy vari-
ants for multiple discrete sources, such as joint entropy, H (X, Y ), conditional entropy,
H(X |Y ), mutual information, H(X ; Y ), relative entropy (or Kullback–Leibler [KL]
distance) for discrete single or multivariate PDFs, D[ pq], and conditional relative
entropy, D[ p(y|x)q(y|x)]. In this chapter, we shall expand our conceptual horizons
by considering the entropy of continuous sources, to which are associated PDFs of
continuous variables. It is referred to as differential entropy, and we shall analyze here its
properties as well as those of all of its above-listed variants. This will require the use of
some integral calculus, but only at a relatively basic level. An interesting issue, which is
often overlooked, concerns the comparison between discrete and differential entropies,
which is nontrivial. We will review different examples of differential entropy, along with
illustrative applications of the KL distance. Then we will address the issue of maximiz-
ing differential entropy (finding the optimal PDF corresponding to the upper entropy
bound under a set of constraints), as was done in Chapter 4 in the discrete-PDF case.
6.1 Entropy of continuous sources
A continuous source of random events is characterized by a real variable x and its
associate PDF, p(x), which is a continuous “density function” over a certain domain
X. Several examples of continuous PDFs were described in Chapter 2, including the
uniform, exponential, and Gaussian (normal) PDFs.
By analogy with the discrete case, one defines the Shannon entropy of a continuous
source X according to:
H(X ) =−
X
p(x)log p(x)dx. (6.1)
As in the discrete case, the logarithm in the integrand is conventionally chosen in
base two, the unit of entropy being bit/symbol. In some specific cases, the defini-
tion could preferably involve the natural logarithm, which defines entropy in units of
nat/symbol. The entropy of a continuous source, as defined above, is referred to as
6.1 Entropy of continuous sources 85
differential entropy.
1
Similar definitions apply to multivariate PDFs, yielding the joint
entropy, H (X, Y ), the conditional entropy, H (X|Y ), the mutual information, H(X ; Y ),
and the relative entropy or KL distance, D( pq) with following definitions:
H(X, Y ) =−
X
Y
p(x, y)log p(x, y)dxdy, (6.2)
H(X |Y ) =−
X
Y
p(x, y)log p(x|y)dxdy, (6.3)
H(X ; Y ) =
X
Y
p(x, y)log
p(x, y)
p(x)p(y)
dxdy, (6.4)
D[ p(x)q(x)] =
X
p(x)log
p(x)
q(x)
dx, (6.5)
D[ p(y|x)q(y|x)] =
X
Y
p(x, y)log
p(y|x)
q(y|x)
dxdy. (6.6)
The above definitions of differential entropies appear to come naturally as the generaliza-
tion of the discrete-source case (Chapter 5). However, such a generalization is nontrivial,
and far from being mathematically straightforward, as we shall see!
A first argument that revealed the above issue was provided by Shannon in his seminal
paper.
2
Our attention is first brought to the fact that, unlike discrete sums, integral sums
are defined within a given coordinate system. Considering single integrals, such as in
Eq. (6.1), and using the relation p(x)dx = p(y)dy,wehave
H(Y ) =−
X
p(y)log[p(y)]dy
=−
X
p(x)
dx
dy
log
p(x)
dx
dy
dy
=−
X
p(x)
log p(x) +log
dx
dy
dx (6.7)
= H (X) −
X
p(x)log
dx
dy
dx
≡ H (X) − C.
1
The term “differential” comes from the fact that the probability P(x ≤ y)isdefinedasP(x ≤ y) =
"
y
x
min
p(x)dx, meaning that the PDF p(x), if it exists, is positive and is integrable over the interval considered,
[x
min
,y], and is also the derivative of P(x ≤ y) with respect to y, i.e.,
p(x) =
d
dy
y
x
min
p(x)dx.
2
C. E. Shannon, A mathematical theory of communication. Bell Syst. Tech. J., 27 (1948), 79–423, 623–56.
This paper can be freely downloaded from http://cm.bell-labs.com/cm/ms/what/shannonday/paper.html.

86 Differential entropy
This result establishes that the entropy of a continuous source is defined within some
arbitrary constant shift C, as appearing in the last RHS term.
3
For instance, it is easy to
show that the change of variable
y = ax,
(a being a positive constant) translates into the entropy shift
H(Y ) = H(X ) +log a.
The shift can be positive or negative, depending on whether a is greater or less than two
(or than e, for the natural logarithm), respectively.
A second observation is that differential entropy can be nonpositive (H (X) ≤ 0)
unlike in the discrete case where entropy is always strictly positive (H(X ) > 0).
4
A
straightforward illustration of this upsetting feature is provided by the continuous uni-
form distribution over the real or finite interval x ∈
[
a, b
]
;
p(x) =
1
b −a
. (6.8)
From the definition in Eq. (6.1), it is easily computed that the differential entropy is
H(X ) = log
2
(b −a). The entropy is zero or negative if b − a ≤ 2(orb −a ≤ e, for the
natural logarithm).
The difference between discrete and differential entropy becomes trickier if one
attempts to connect the two definitions. This issue is analyzed in Appendix E. The
comparison consists in sampling, or “discretizing” a continuous source, and calculating
the corresponding discrete entropy, H
. The discrete entropy is then compared with the
differential entropy, H
. As the Appendix shows, the two entropies are shifted from each
other by a constant n =−log , or H
= H
+ n. The constant n corresponds to the
number of extra bits required to discretize the continuous distribution with bins of size
= 1/2
n
. The key issue is that in the integral limit n →∞or → 0, this constant
is infinite! The conclusion is that an infinite discrete sum, corresponding to the integral
limit → 0, is associated with an infinite number of degrees of freedom, and hence,
with infinite entropy.
The differential entropy defined in Eq. (6.1), as applying to any integration domain X ,
is always finite, however. This proof is left as an (advanced) exercise. In the experimental
domain, calculations are always made in discrete steps. If the source is continuous,
the experimentally calculated entropy is not H
, but its discretized version H
, which
assumes a heuristic sampling bin . The constant n =−log should then be subtracted
from the discrete entropy H
in order to obtain the differential entropy H
, thus ensuring
reconciliation between the two concepts.
3
For multivariate expressions, e.g., two-dimensional, this constant is
C =
X,
Y
p(x, y)log
J
x
y
dxdy,
where J (x/y) is the Jacobian matrix.
4
Excluding the case of a discrete distribution where p(x
i
) = δ
ij
(Kronecker symbol).
