Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

7.2 The Turing machine 97

Entering the AIT domain simply requires one to acknowledge the following three

basic deﬁnitions:

(a) The complexity K (x) is deﬁned as the smallest size of a program q(x) necessary to

generate the sequence x.

(b) Such a program is a ﬁnite set of binary instructions with a length of

q(x)

bits.

The smallest program size, min

q(x)

= K (x), which is called the complexity of x,

is equivalently referred to as algorithmic information content, algorithmic complexity,

algorithmic entropy,orKolmogorov complexity (also called Kolmogorov–Chaitin com-

plexity and sometimes noted KC(x) instead).

The Turing machine, which is named after

its inventor, A. Turing,

can be viewed as the most elementary and ideal implementation

of a computer, and is, as we shall see, of inﬁnite computation power (due to speed, not

memory size).

To clarify and develop all of the above, we ought ﬁrst to understand what a Turing

machine looks like and how it works; this is addressed in the next section. Then we will

investigate Kolmogorov complexity and its properties. Interestingly, I will show that

Kolmogorov complexity is in fact incomputable! Finally, I will show that Kolmogorov

complexity and Shannon’s entropy are symptotically bounded, a most remarkable feature

considering the previous property.

7.2 The Turing machine

The Turing machine (TM) is an abstract, idealized, or paper version of the simplest and

most elementary computing device. As Fig. 7.1 illustrates, it consists of a tape and a

read/write head. The tape is of indeﬁnite length and it contains a succession of memory

cells, into which are written the bit symbols 0 or 1.

By convention, cells that were never

written or were left blank are read as containing the 0 bit. The tape can be made to move

left or right by one cell at a time.

The operations of the head and tape are deﬁned by a table of instructions

{

, I

,...,I

}

of ﬁnite size N , also called an action table. The action table is not

a program to be read sequentially. Rather, it is a set of instructions corresponding to dif-

ferent possibilities to be considered by the machine, as I shall clarify. At each instruction

step, the machine’s head is initially positioned at a single tape cell.

See, for instance: http://en.wikipedia.org/wiki/Kolmogorov_complexity, http://szabo.best.vwh.net/

kolmogorov.html.

See, for instance: http://plato.stanford.edu/archives/spr2002/entries/turing-machine/, http://en.wikipedia.

org/wiki/Universal_Turing_machine, www.turing.org.uk/turing/, www.alanturing.net/, www.cs.usfca.edu/

www.AlanTuring.net/turing_archive/pages/Reference%20Articles/What%20is%20a%20Turing20Machine.

html.

More generally, the symbols that can be put into the cells, including a conventional blank symbol, could be

selected from any ﬁnite alphabet.

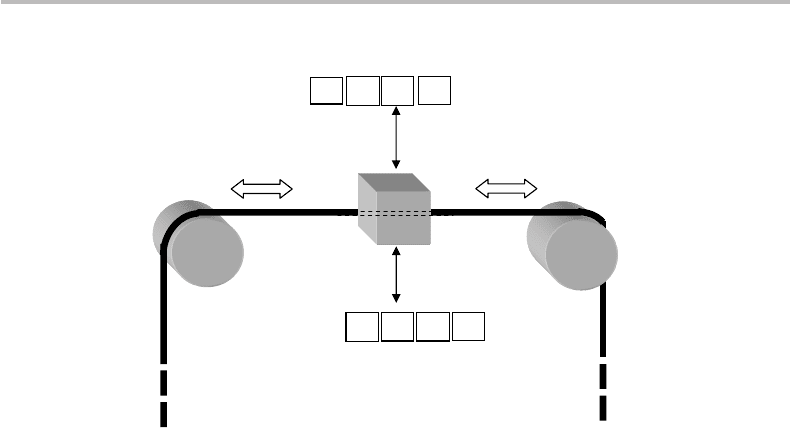
98 Algorithmic entropy and Kolmogorov complexity

0 1

Instructions

Cells

Tape

Head

State 3

…

……

Figure 7.1 Schematic representation of Turing machine.

The machine is said to be in an input state s

, which corresponds to a speciﬁc

instruction in the action table. This instruction tells the machine to perform three basic

operations altogether:

(a) Given the cell’s content, what new content (namely, 1 or 0) is to be written into the

cell;

(b) In what direction the tape should be moved, namely, left or right;

the machine should be moved.

For instance, given the input state s

the corresponding instruction could be:

(a) If reading 0 then write 1,

(b) Move tape to the left,

If the cell reading is 0, the machine changes the contents, then moves according to

the two other actions, (b) and (c). If the cell reading is 1, then it halts. To cover

this other possibility, a second instruction can be introduced into the action table, for

instance;

(a) If reading 1 then write 0,

(b) Move tape right,

These two sets of instructions in the action table can be summarized as follows:

;0→ 1; L; s

(7.1)

;1→ 0; R; s

Since the instructions move the TM into new states s

, s

, the instructions corresponding

to input states s

, s

should also be found in the table. There are no restrictions concerning

7.2 The Turing machine 99

Table 7.1 Example of action table for Turing machine.

Input state Change of cell contents Move tape (R, right; L, left) Output state

0 → 1R s

0 → 0R s

0 → 1R s

0 → 1L s

Table 7.2 Tape changes during Turing machine computation, using the action table deﬁned

in Table 7.1. The input tape is blank, representing a string of 0 bits or 0000000 ... The

initial position of the head is on the leftmost zero bit. At each step, the position of the head

on the tape is shown by the bold, underlined bit. The machine halts at step 6, leaving the

codeword 1101100 ...on the output tape.

Step Input state Tape contents Output state

1 s

0 000000... s

2 s

1 0 00000... s

3 s

110 0000... s

4 s

1100 000... s

5 s

11010 00... s

6 s

1101 100... ?

Halt

the possibility of returning to a state previously used as an input (e.g., s

;0→ 1; R; s

If there is no output state corresponding to the instruction, the machine halts. The same

happens if the cell reading is not a case covered by the action table given a new input

state.

To summarize, the tape and machine keep on moving, as long as the combination

of initial state and cell reading have a matching deﬁnition in the action table. The ﬁnal

output of the program is the bit sequence written on the tape, which is left at the point

where the machine halted. To illustrate how the TM works, consider next a few program

examples including the basic operations of addition, subtraction, multiplication, and

division.

Example 7.1

This is a TM program that creates the 5-bit sequence 11011 out of an initially blank

tape with equivalent sequence 0

0000 ... Table 7.1 shows the action table instructions

and Table 7.2 shows the step-by-step implementation on the tape. It is assumed that the

ﬁrst initial state is s

and that the head is located at the leftmost cell, as underlined. As

Table 7.2 illustrates, each of the computation steps is characterized by a left-to-right tape

move (or equivalently, right-to-left head move, as viewed from the tape) with a possible

change in the cell contents. It is seen that the machine halts at step 6, because there is

no instruction in the action table concerning an input state s

with a cell reading of 1.

100 Algorithmic entropy and Kolmogorov complexity

Table 7.3 Example of action table for Turing machine deﬁning

the addition of two numbers in the unary system.

Input Change of cell Move Output

state contents tape state

1 → 1Rs

0 → 0Rs

1 → 1Rs

0 → 0Ls

1 → 0Ls

0 → 1Rs

Example 7.2

This is a TM program that adds two integers. Such an operation requires one to use the

unary system. In the unary system, the only symbol is 1 (for instance) and an integer

number n is represented by a string of n consecutive 1s. The decimal numbers 3 and 7

are, thus, represented in unary as 111 and 1111111, respectively. Adding unary numbers

is just a matter of concatenating the two strings, namely, 3 +7 ≡ 111 +1111111 =

1111111111 ≡ 10. Because we are manipulating two different numbers, we need an

extra blank symbol, 0, to use as a delimiter to show where each of the numbers ends.

Thus, the two numbers, 2 and 3, must be noted as the unary string 1101110. We use this

string as the TM input tape.

The action table and the step-by-step implementation of its instructions are shown

in Table 7.3 and 7.4, respectively. It is seen that the TM halts at step 14. The output

tape then contains the string 1111100 ≡ 5, which is the expected result. It is left to the

reader as an exercise to show that the program also works with other integer choices,

meaning that this is a true adding machine! We note that the program only requires four

states with two symbols, which illustrates its simplicity. The output state s

, which is

undeﬁned, forces the TM to halt. Analyzing the tape moves line by line in Table 7.4,we

can better understand how the algorithm works.

Basically, each time the head sees a 1 in the cell, the only action is to look at the next

cell to the right, and so on, until a 0 input is hit (here, at step 3). The head then inspects

the next cell with input state s

If the result is another 0, then the output state is s

, meaning that the machine must

halt at the next step, the output tape remaining as it is. This is because reading two

successive 0 means that either (a) the second operand is equal to zero, or (b) that the

addition is completed.

If the result is a 1, then the program ﬂips the two cell values from 01 to 10, and

the same inspection as before is resumed, until another 0 is hit (here, at step 12). If

the sequence 00 is identiﬁed from there, the TM halts, meaning that the addition is

completed.

7.2 The Turing machine 101

Table 7.4 Tape changes during Turing machine computation, using the action table

in Table 7.3, which deﬁnes the addition of two numbers. The input tape is set to

1101110, which in unary corresponds to the two numbers 2 ≡11 and 3 ≡111, as

delimited by the blank symbol 0. The initial position of the head is on the leftmost

bit. The output tape is seen to contain the string 1111100 ≡5.

Step Input state Tape contents Output state

1 s

1101110 s

2 s

1101110 s

3 s

1101110 s

4 s

1101110 s

5 s

1100110 s

6 s

1110110 s

7 s

1110110 s

8 s

1110010 s

9 s

1111010 s

10 s

1111010 s

11 s

1111000 s

12 s

1111100 s

13 s

1111100 s

14 s

1111100Halt

Performing the addition of large numbers only increases the number of computation

steps and the overall computation time. But since the tape is inﬁnite, there is no problem

of overﬂow. The TM is, however, not capable of handling inﬁnite numbers, or real

numbers with an inﬁnity of decimal places, as I shall discuss later.

Example 7.3

This concerns the operation of subtraction. It is performed in a way similar to addi-

tion, e.g., 7 −3 ≡ 1111111 −111 = 1111 ≡ 4. Assume ﬁrst that the ﬁrst operand (i )

is greater than or equal to the second operand ( j). Table 7.5 shows an action table

performing the subtraction and outputting k = i − j.Itisleftasanexercisetoverify

how the proposed algorithm (call it Sub0) effectively works.

If the ﬁrst operand (i) is strictly less than the second (j), or i < j,wemustuse

a subtraction algorithm different from Sub0; call it Sub1. The problem is now to

determine which out of Sub0orSub1 is relevant and must be assigned to the TM. We

must then deﬁne a new algorithm, call it Comp, which compares the two operands (i, j)

and determines which of the two cases, i ≥ j or i < j, applies. It is left as an exercise

to determine an action table for implementing Comp. Based on the output of Comp,the

TM can be then assigned to perform either Sub0orSub1, with the additional information

from Comp that the result of the subtraction is nonnegative (k = i − j ≥ 0) or strictly

negative (k = i − j ≤ 0). Note that the case i = j (k = 0) is implicit in the output of

Sub0.

102 Algorithmic entropy and Kolmogorov complexity

Table 7.5 Example of action table for Turing machine deﬁning the

subtraction of two numbers i, j (i ≥ j ) in unary system.

Change of Move Output

Input state cell contents tape state

0 → 0Rs

1 → 1Rs

0 → 0Rs

1 → 0Ls

B → B R s

0 → 0Ls

1 → 0Rs

I will not develop the analysis further here, or a full TM program for subtraction.

Sufﬁce it to realize that Sub1 can be implemented as a mirror algorithm of Sub0,

proceeding from right to left, or performing the operation k



= j − i . The information

printed by Comp on the tape tells whether the output of the subtraction is positive or

negative (noting that the case i = j (k = 0) is implicit in the output of Sub0). The lesson

learnt is that the TM is capable of performing subtraction in the general case, should the

algorithm and corresponding action table cover all possible cases, with the TM halting

on completion of the task. It is left as an exercise to analyze how such a program can

be implemented. This exercise, and the preceding ones, should generate a feeling of

intimacy with the basic TM. As we will see, the TM reserves some surprises, and this is

why we should enjoy this exploration.

Example 7.4

This concerns the operation of multiplication. A TM program performing the multipli-

cation of two integers,

is shown in Table 7.6.

The directions of the move are either > (right) or < (left). As in previous examples,

the two numbers to multiply and written in the input tape must be expressed in the

unary system, with the convention that integer n is represented by a string of n + 11s

(0 ≡ 1, 1 ≡ 11, 2 ≡ 111, 3 ≡ 1111, etc.). Here, I have introduced a supplemental start

instruction (1,_,1,_,>) to position the head to the second cell to the right and the TM in

input state 1. This instruction ensures that the program can be run with various simulators

available on the Internet.

It is seen from Table 7.6 that the multiplication program

requires as much as 15 states, plus the undeﬁned “halt” state. Also, the TM must be able

to handle (or read and write) six different symbols including the “blank” underscore,

which corresponds to an absence of read/write action (and is not to be confused with

See www.ams.org/featurecolumn/archive/turing_multiply_code.html and the line-by-line comments to ana-

lyze the corresponding algorithm. This program can be tested in Turing machine simulators avail-

able on the Internet, see for instance: http://ironphoenix.org/tril/tm/, www.turing.org.uk/turing/scrapbook/

tmjava.html, www.cheransoft.com/vturing/index.html.

See, for instance: http://ironphoenix.org/tril/tm/, www.turing.org.uk/turing/scrapbook/tmjava.html, www.

cheransoft.com/vturing/index.html.

7.2 The Turing machine 103

Table 7.6 Action table for Turing machine multiplication program. The table contains

38 instructions using 15 states numbered 1, . . . , 15, plus the halt state (H), and

six symbols noted 1, X, Y, Z, W plus the underscore _, which stands for blank. The

instruction nomenclature is “input state, read symbol, output state, write symbol, move

right (>)orleft(<).” The numbers m, n to be multiplied are entered in the input tape

under the string form

M N ,whereM and N are strings of m + 1 and n + 1

successive 1s, respectively. The head is initially located to the leftmost (blank) symbol.

The output tape takes the form

M N P ,whereP is the unary representation of

mn = p (P is a string of p + 1 successive 1s).

1 1, ,1, , > 20 10, , 11, , <

2 1, 1, 2, W, > 21 10, 1, 12, Z, >

3 2, 1, 2, 1, > 22 12, 1, 12, 1, >

4 2,

,3, , > 23 12, , 13, , >

5 3, 1, 4, Y, > 24 13, 1, 13, 1, >

6 4, 1, 4, 1, > 25 13,

, 14, 1, <

7 4,

,5, , > 26 14, 1, 14, 1, <

8 5,

,6,1,< 27 14, , 14, , <

9 6,

,6, , < 28 14, Z, 10, Z, >

10 6, 1, 6, 1, < 29 14, Y, 10, Y, >

11 6, Z, 6, Z, < 30 11, 1, 11, 1, <

12 6, Y, 6, Y, < 31 11,

, 11, , <

13 6, X, 7, X, > 32 11, Z, 11, 1, <

14 6, W, 7, W, > 33 11, Y, 6, Y, <

15 7,

,8, , > 34 8, Y, 8, 1, <

16 7, 1, 9, X, > 35 8,

,8, , <

17 9, 1, 9, 1, > 36 8, X, 8, 1, <

18 9,

,9, , > 37 8, W, 15, 1, <

19 9, Y, 10, Y, > 38 15,

,H, , >

an erase/blank character). The table also shows that 38 different instructions, or TM

transitions, are necessary to complete the multiplication of the two input numbers.

To recall, such an operation can be performed with any numbers of any size, without

limitation in size, since the TM tape is theoretically inﬁnite in length. I will come back

to this point later.

Example 7.5

This concerns the operation of division, which is also relatively simple to implement

with a TM. Given two integers m, n, the task is to ﬁnd the quotient [m/n] and the

remainder r = m − n[m/n], where the brackets indicate the integer part of the ratio

m/n. A ﬁrst test consists in verifying that n > 0, i.e., that the ﬁeld containing n has at

least two 1s (with the convention 1

decimal

≡ 110

unary

). This test can be performed through

the above-described Comp program, which is also derived in an exercise. If n = 0, a

special character meaning “zero divide” must be output to the tape and the TM must

be put into the halt state. A second test consists in checking whether m ≥ n or m < n,

which is again performed by the Comp program. In the second case (m < n), the TM

must output [m/n] = 0 and r = 0, and then halt. In the ﬁrst case (m ≥ n), the TM must

104 Algorithmic entropy and Kolmogorov complexity

compute the value of the quotient [m/n] ≥ 1. Computing [m/n] is a matter of iteratively

removing a string copy of n from m, while keeping count of the number of removals,

k. This is equivalent to performing the subtraction m − n through the above-described

program Sub0, iterated as many times (k) as the result of Sub0 is nonnegative. The

remainder r is the number of 1s remaining in the original m ﬁeld after this iteration. See

Exercise 7.5 for a practical illustration of this algorithm.

A key application of division concerns data conversion from unary to binary (or to

decimal). It is a simple exercise to determine the succession of divisions by powers of

two (or powers of ten) required to retrieve the digits (or decimals) of a given unary

number. Similarly, multiplication and addition can be used to convert data from binary

(or decimal) into unary. It is given as an exercise to determine an algorithm involving

a succession of multiplications and additions necessary to perform such a conversion,

given a binary (or decimal) number. The key conclusion is that both input and output

TM tapes can be formatted into any arbitrary M-ary number representation (assuming

that the head has the capability to read/write the corresponding M symbol characters),

while the unary system is used for the TM computations. The TM is, thus, able to

manage all number representations for input and output, which illustrates that it is a

truly fundamental computing machine, as we may realize increasingly through the rest

of this chapter.

It is most recommended to explore the previously referenced Internet sites, which

present live TM simulators, and thus make it possible to visualize that Turing machine

at work. Some of these simulators include Java applets, from which ready-made TM

programs may be selected through pop-up menus and then executed. Some of these sites

make it possible to create and test one’s own programs, with the option to run them

either step by step or at some preselected speed. It is quite fascinating to observe in

real-time the execution of a TM program, as it conveys the impression of an elementary

intelligence. But let us not be mistaken, the intelligence is not that of the machine, but

of the human logic that built the action table!

We may wonder how long it takes the TM to perform big operations, or operations

involving big operands. Actually, we ought to measure it not by mere execution time,

but by the number of required TM transitions from start to halt states. Such transitions

are the elementary tape moves from one TM state to the next TM state, passing through

one cell at a time. Recalling that the TM is not a physical machine, it can be made

with arbitrarily small size and arbitrarily high speed, so that the execution time for any

single transition is not a relevant parameter. The number of states deﬁned in the action

table provides a measure of the complexity of the algorithm (the word “complexity”

is not chosen here by chance, as we shall see later on). But as we know, the TM can

use any of these states several times before reaching the halt state, therefore, a simple

algorithm may have a long execution length. Also, the size of the input and of the output

data affects the execution length. For instance, a simple character-erasure algorithm may

take as many transitions as there are symbol characters in the input data. Therefore, the

relevant parameter to measure the execution length is the number of transitions required

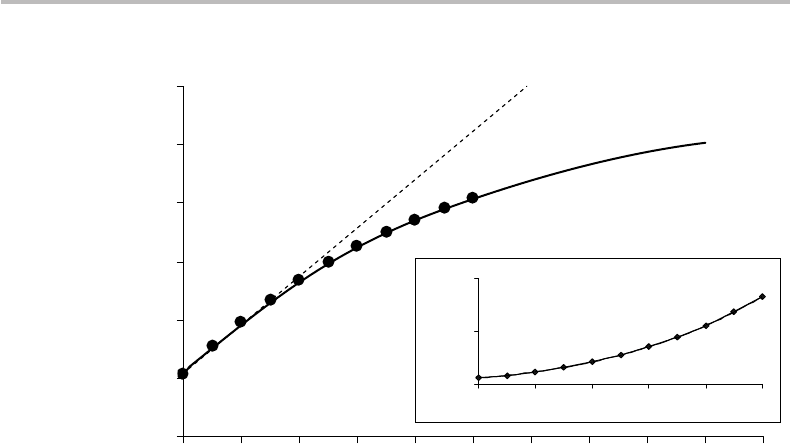
7.2 The Turing machine 105

0 2 4 6 8 101214161820

Integer to be squared

Number of transitions

100 000

200 000

10 12 14 16 18 20

Figure 7.2 Number of Turing-machine transitions to compute the square of small integers,

according to action-table program deﬁned in Table 7.6. The dots correspond to results obtained

with a Turing-machine simulator up to n = 10, the smooth line corresponds to a sixth-order

ﬁtting and extrapolation polynomial up to n = 20. The inset shows the same data from n = 10

to n = 20 in linear plot with a fourth-order ﬁtting.

to execute the full algorithmic computation, and depends on the sizes of the input and

of the output.

To provide a sense of computation length, let us look at a practical example. Consider,

for instance, the following question: “Given two numbers of maximum size n,how

many TM transitions are required to perform their multiplication?” We may answer

this question by analyzing the operation of squaring integers, as ranging from n =0to

n =20, and each time count the number of transitions. The action table corresponds to

that of Table 7.6, with n, n for the two input operands. Figure 7.2 shows a plot of the

transition counts, as obtained from a TM simulator up to a maximum computation power

of n =10. Polynomial extrapolation makes it possible to evaluate the result up to n =20,

either in logarithmic or linear scales. It is observed from the ﬁgure that the number of

transitions to compute n

is subexponential to the integer size n.Forn = 0 −1, the

computation requires 12–35 transitions; for n = 10, it requires 11 825 transitions, and

for n = 20 the result is evaluated to be 170 851. The fact that the trend is subexponential

can be simply explained by the following argument: for sufﬁciently large n,theTMis

essentially found in the states that move the machine towards (state 13) and back to (state

14) the right-hand side of the tape in order to store the 1 symbols deﬁning the result.

Each time the trip is one cell longer. With the relation 2



k=1

k = N (N + 1), where k

is the number of cell moves to the result ﬁeld to write 1 and N = n

the total number

of round-trips, we can evaluate the number of transitions as asymptotically ≈ N

= n

This is precisely why the linear curve in Fig. 7.2 is very well ﬁtted by a fourth-order

106 Algorithmic entropy and Kolmogorov complexity

polynomial. We can thus conclude that for squaring an integer n, the number of TM

computations (or transitions) is asymptotically n

: the result of squaring integer n is a

string of n

+ 1 symbols, but it takes n

head moves to write the result onto the tape.

In the preceding ﬁve application examples, I have illustrated how the TM can perform

various types of basic computations. In all cases, integers were used. But what about real

numbers? Can Turing machines also perform computations with real numbers? These

are the questions we address next.

Considering real numbers, we ought ﬁrst to distinguish two cases. First, a real number

n is associated with a size

, which ranges from zero to inﬁnity. Second, some real

numbers are nonintegers, and, therefore, are deﬁned through a certain suite of decimal

places. The suite can be of ﬁnite size, such as 5/4 = 1.25 (the other decimal places

being zero), or of inﬁnite size, such as 1/3 = 0.333333 ... or 13/11 = 1.181818 ...

(decimals, or patterns of decimals, being inﬁnitely repeated). We will consider later on

the case of numbers whose inﬁnite decimal suites do not exhibit patterns (irrational

and transcendental numbers, whose decimals may or may not be computable through a

polynomial equation).

Just as with our physical computers, real numbers with ﬁnite size and ﬁnite numbers of

decimal places can be handled by the TM through the exponent format n = p

× 10

more generally through any type of ﬂoating-point representation. For instance, 203.5 =

2.0350 × 10

= 20.350 ×10

= 2035.0 × 10

−1

are three possibilities for the same real

number 203.5. The case where the number of decimal places is inﬁnite can also be

processed by a TM, but only up to some truncation level, just as with any physical

computer. For instance:

13/11 = 1.1181818 ... ≈ 1.11818 ×10

≈ 1.1181 ×10

≈ 1.118 × 10

...,and so on.

Concerning transcendental numbers,

like π or e, we may think that because of its

inﬁnite memory size, the TM could have an advantage over a physical computer. Alas,

the number of decimals for such numbers being inﬁnite, the TM would also never halt

in the task of performing its inﬁnite computation, and this points to the same problem

of truncation. It is then possible to devise a TM program that outputs the decimal places

of π or e, and stores them on the TM tape, but the machine would never halt unless the

program included an algorithmic counter to set a limit to the output’s size. The same

restriction applies to physical computers, with the difference that the limit is intrinsically

deﬁned by memory size and execution time.

It would appear from the above analysis and conclusions that any real number having

an inﬁnite number of decimal places, including transcendental or irrational numbers,

such as π,e,

√

2 ..., is TM computable, at least up to some truncation level. But it turns

out to our surprise that this is not the case!

Meaning numbers that are not a solution of any polynomial equation; not to be confused with irrational

numbers (such as

√

2) which apply to this case (namely, here, the solution of x

− 2 = 0). See for instance

http://en.wikipedia.org/wiki/Transcendental_number.