Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

7.4 Kolmogorov complexity 117

For instance, n = 11, or 1011 in binary, is encoded as m = 1100111101. This is not a

minimal-length code (as compression algorithms exist), but it surely deﬁnes n.Wesee

that this code length is 2 log n + 2 = 2logl(x) + 2. The basic program that describes x

and that can tell the TM to halt after outputting n bits is the same as that which prints x bit

by bit (q

), but with an additional instruction giving the value of n. Based on Eq. (7.14)

and the above result, the length of such a program is, therefore,

(x)

= K [x

l(x)] +

c +2logl(x) +2 ≈ K [x

l(x)] + 2logl(x) + c for sufﬁciently long sequences. But

as we know, if x can be described by some algorithm, the corresponding program

length is such that

q(x)

≤

(x)

, meaning that the complexity of x has the upper

bound

K (x) ≤ K [x

l(x)] + 2logl(x) + c. (7.15)

We have established that the complexity K (x) of any string x has an upper bound deﬁned

by either Eq. (7.14)orEq.(7.15).

The knowledge of an upper bound for complexity is a valuable piece of information,

but it does not tell us in general how to measure it. An important and most puzzling

theorem of algorithmic information theory is that complexity cannot be computed.This

theorem can be stated as follows:

There exists no known algorithm or formula that, given any sequence x, a Turing machine can

output K (x).

This leads one to conclude that the problem of determining the Kolmogorov complexity

of any x is undecidable! The proof of this surprising theorem turns out to be relatively

simple,

as shown below.

Assume that a program q exists such that a UTM can output the result U [q(x)] = K (x)

for any x. We can then make up a simple program which, given x, could ﬁnd at least

one string having at least the same complexity as x, which we call K (x) ≡ K. Such a

program r is algorithmically deﬁned as follows:

Input K ,

Fo r n = 1toinﬁnity,

Deﬁne all strings s of length n,

If K (s) ≥ K print s then halt,

Continue.

This program has a length

+ 2logl(K ) + c. Since the program length grows

as the logarithm of K , there exists a value K for which

r(K )

< K . The program

eventually outputs a string s of complexity K (s) ≥ K >

, which is strictly greater

than the program size! By deﬁnition, the complexity K (s)ofs is its minimum descriptive

length. By deﬁnition, however, there is no TM program that can output s with a length

shorter that K (s). Therefore, the hypothetical program q, which computes K (x)given

x, simply cannot exist. Complexity cannot be computed by Turing machines (or, for that

matter, by any computing machine).

As adapted from http://en.wikipedia.org/wiki/Kolmogorov_complexity.

118 Algorithmic entropy and Kolmogorov complexity

∅

1, 0

00, 01, 10, 11

(

)

211

…, 1010111…, …

−1

…

Figure 7.3 Enumeration of bit strings of size k = 0tok = K − 1.

While complexity cannot be computed, we can show that it is at least possible to

achieve the following:

(a) Given a complexity K , to tell how many strings x have a complexity less than K ,

i.e., satisfying K (x) < K ;

(b) For a string of given length n, to deﬁne the upper bound of its complexity, namely,

to ﬁnd an analytical formula for the upper bound of K [x

l(x)] in Eq. (7.15).

To prove the ﬁrst statement, (a), is a matter of ﬁnding how many strings x have a

complexity below a given value K , i.e., satisfying K (x) < K . This can be proven by

the following enumeration argument. Figure 7.3 shows the count of all possible binary

strings of length k,fromk = 0 (empty string) to k = K − 1. The sum of all possibilities

illustrated in the ﬁgure yields

K −1



k=0

n(k) =

K −1



k=0

1 − 2

= 2

− 1 < 2

. (7.16)

Each of these possible strings represents a TM program, to which a unique output x

corresponds. There are fewer than 2

programs smaller than K , therefore there exists

fewer than 2

strings of complexity < K .

The statement in (b) can be proven as follows. Given any binary string x of length n,we

must ﬁnd the minimal-length program q that outputs it. Assume ﬁrst that the string has k

bits of value 1, thus n − k bits of value 0, with 0 < k < n. We can then create a catalog of

all possible strings containing k 1s, and index them in some arbitrary order. For instance,

with n = 4 and k = 2, we have x

= 1100, x

= 1010, x

= 1001, x

= 0101, x

0011, x

= 0110. Having this catalog, we can simply deﬁne any string x

according to

some index i.Givenn and k, the range of index values i is C

= n!/[k!(n − k)!], which

represents the number of ways to assign k 1s into n bit positions. The program q deﬁning

x must contain information on both k and i . As we have seen, it takes 2 log k + 2 bits

to deﬁne k by repeating its bits, with a two-bit delimiter at the end (noting that fancier

compression algorithms of shorter lengths also exist). The second number i can be

deﬁned after the delimiter, but without repeating bits, which occupies a size of log C

bits. We must also include a generic program, which, given k, generates the catalog.

Assume that its length is c, which is independent of k. The total length of the program

q is, therefore,

q(k, n)

= 2logk + 2 +log C

+ c ≡ 2logk + log C

+ c



. (7.17)

7.4 Kolmogorov complexity 119

The next task is to evaluate log C

. Using Stirling’s formula,

it is possible to show that

for sufﬁciently large n:

log C

≈ log

√

2π

+ nf





, (7.18)

where the function f is deﬁned by f (u) =−u log u − (1 −u)log(1− u), and, as usual,

all logarithms are in base 2. The function f (k/n) is deﬁned over the interval 0 < k/n <

1. To include the special case where all bits are identical (k/n = 0ork/n = 1) we can

elongate the function by setting f (0) = f (1) = 0, which represents the analytical limit

of f (y) for real y. We note that f (u) is the same function as deﬁned in Eq. (4.14)for

the entropy of two complementary events. Its graph is plotted in Fig. 4.7, showing a

maximum of f (1/2) = 1foru = 1/2.

Substituting Eq. (7.18) into Eq. (7.17), we, thus, obtain:

q(k, n)

≈ 2logk + nf





+ c



, (7.19)

where c



is a constant. Consistently, this program length represents an upper bound to

the complexity of string x with k 1s, i.e.,

K (x

ones

) ≤ 2logk + nf





+ c



. (7.20)

In the general case, a string x of length n can have any number k of 1 bits, with 0 <

k/n < 1. We ﬁrst observe that the integer k is deﬁned by the sum of the a

bits forming

the string, namely, if x = a

n−1

...a

= 0or1)wehavek =



j=1

. Second,

we observe that since k < n we have log k < log n. Based on these two observations,

the general approximation formula giving the upper bound for the complexity K (x

n )

of any binary string of length n deﬁned by x = a

n−1

...a

= 0or1),is:

K (x

n ) ≤ 2logn + nf







j=1





+ c



. (7.21)

To recall, Eq. (7.21) represents the Stirling approximation of the exact deﬁnition:

K (x

n ) ≤ 2logn + log C

+ c. (7.22)

See Eq. (A9)inAppendix A.

Applying Stirling’s formula yields, after some algebra:

≈

√

2π

exp





1 +



ln(n) −





ln(k) −



1 −







1 −

%

In the limit n  1, and after regrouping the terms, the formula reduces to:

≈

√

2π

exp





−





−



1 −





1 −

%

√

2π

nf(k/n)

where

f (u) =−u

ln u

ln 2

− (1 −u)

ln u

ln 2

(1 −u) ≡−u log

u − (1 −u)log

(1 −u).

120 Algorithmic entropy and Kolmogorov complexity

0 10 20 30 40 50 60 70 80 90 100 110 120 130

String

Complexity

= 2

= 3

= 4

= 5

= 7

= 6

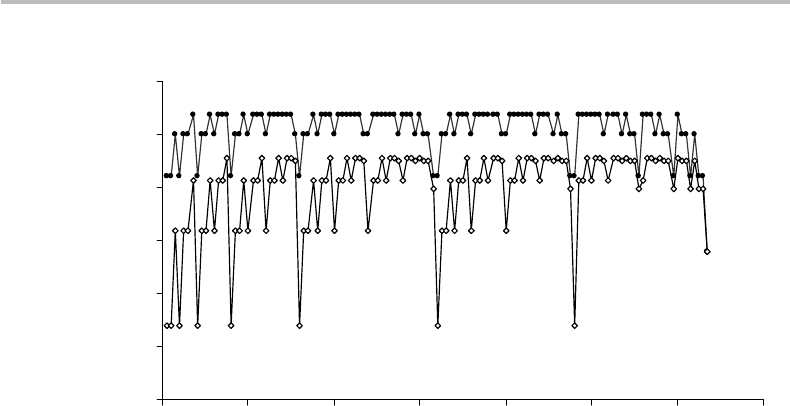
Figure 7.4 Upper bound of conditional complexity K (x

n ) for each binary string x of exactly n

bits (n = 2ton = 7), as deﬁned by Eq. (7.21) with the Stirling approximation (open symbols),

and as deﬁned by Eq. (7.22) without approximation (dark symbols). In each series of size n,the

strings x are ordered according to their equivalent decimal value.

Figure 7.4 shows plots of the upper bound of K (x

n ) for each binary string of exactly n

bits, according to (a) the Stirling approximation in Eq. (7.21) with c



= log(1/

√

2π) + c

(taking c = 0), and (b) the corresponding exact deﬁnition in Eq. (7.22), also taking c = 0.

For each series of length n, the strings x are ordered according to their equivalent decimal

value (e.g., x = 11 corresponds to x = 1011 in the series n = 4, x = 01011 in the series

n = 5, x = 001011 in the series n = 6, etc.).

We ﬁrst observe from the ﬁgure that the upper bound of K (x

n ) oscillates between

different values. For even bit sequences (n even), the absolute minima are obtained

for f (u) = 0orC

= 1, and correspond to the cases where all bits are identical. The

absolute maxima are obtained for f (u) = 1orC

= 0.5, which corresponds to the cases

where there is an equal number of 0 and 1 bits in the string. For odd bit sequences (n

odd), the conclusions are similar with all bits identical but one (minima) or with an

approximately equal number of 0 and 1 bits in the string.

Second, we observe that the approximated deﬁnition (Eq. (7.21)) and the exact deﬁni-

tion (Eq. (7.22)) provide nearly similar results. It is expected that the difference rapidly

vanishes for string lengths n sufﬁciently large.

Third, we observe that the complexity is generally greater than the string length

n, which appears to be in contradiction with the result obtained in Eq. (7.14), i.e.,

K [x

l(x) = n ] ≤ n + c. Such a contradiction is lifted if we rewrite Eq. (7.21)inthe

form:

K (x

n ) ≤ n



2logn

+ f









(7.23)

7.4 Kolmogorov complexity 121

0 20406080100120140

String

Complexity

Figure 7.5 Upper bound of conditional complexity for each binary strings x of length n = 7:

K (x

n ), as deﬁned by Eq. (7.22) (dark symbols) and K (x

n, k ), as deﬁned by Eq. (7.24) (open

symbols) with k being the number of 1s in the string.

and take the limit for large n, which gives K (x

n ) ≤ nf(k/n) ≤ n = l(x). The upper

bound n = l(x) stems from the fact that f (u) varies from zero to unity. It is a maximum

for u = k/n = 0.5, which corresponds to the case where there is an equal number of 0

or 1 bits in the string. In the case where the number of 1 bits in the string is known, we

have also established from the above that

K (x

n, k

ones

) ≤ 2logk + log C

+ c. (7.24)

It is exactly the same result as in Eq. (7.22) with log n replaced by log k (k ≥ 1). Since

k ≤ n, the upper bound of K (x

n, k

ones

) is, therefore, lower than that of K (x

n ). The

comparison between the two deﬁnitions is shown in Fig. 7.5 for n = 7. We observe from

the ﬁgure that K (x

n, k

ones

) has a ﬁner structure than K (x

n ) as we scan the string

catalog from x = 0000000 to x = 1111111, which reﬂects the periodic changes in the

number of 1 bits within each of the strings.

Consider next the following problem: given two strings x and y, what is the size of

the smallest program that can output both x and y simultaneously?

A ﬁrst possibility is that x and y are algorithmically independent, i.e., there is no

algorithm q that is capable of computing both x and y.Letq

and q

= q

)be

the two programs describing x and y, respectively, from the same universal Turing

machine U (i.e., U[q

] = x, U [q

] = y). We can then chain the two programs to form

= q

, a program that computes x then y. There is no need for any additional

instruction to the machine. Therefore, the program length is simply |q

|=|q

|+|q

The minimal length of such a program is:

K (x, y) = min

|=min

|+min

|≡K (x) + K (y), (7.25)

122 Algorithmic entropy and Kolmogorov complexity

which shows that if two strings are algorithmically independent their joint complexity

K (x, y) is given by the sum of their individual complexities. It is clear that K (x, y) =

K (y, x). What if x and y are not algorithmically independent? This means that the

computation of x provides some clue as to the computation of y. A program calculating

y could be q

= q

. The machine U ﬁrst computes x then uses the program q

compute y.

Next, we shall deﬁne the conditional complexity K (y

) , which represents the

minimal size of a program describing y given the program describing x. It is also noted

K (y

x∗), with x∗=q

, or, for simplicity, K (y

x ). This last notation should be used

with the awareness that

x is a condition on the program q

, not on the string x.

The issue of ﬁnding the minimal size of q

= q

is far from trivial. Chaitin

showed

that

K (x, y) ≤ K (x) + K (y

x ) +c

↔ (7.26)

K (y

x ) = K (x, y) − K (x) +c



where c represents a small overhead constant, which is one bit for sufﬁciently long

strings. The second inequality stems from the ﬁrst, with c



≥ 0 being a nonnegative

constant.

Since the joint complexity K (x, y) is symmetrical in the arguments x, y,we

also have

K (x

y ) = K (x, y) − K (y) +c



. (7.27)

If x and y are algorithmically independent, it is clear that q

y|x

= q

(there is no clue

from x to compute y), or equivalently K (y

x ) = K (y), and likewise, K (x

y ) = K (x).

In this case, K (x, y) = K (x) + K (y) +c



We can now deﬁne the mutual complexity K (x; y)ofx and y (note the delimiter “;”)

according to either of the following:







K (x; y) = K (x) + K (y) − K (x, y)

K (x; y) = K (x) − K (x

y ) +c



K (x; y) = K (y) − K (y

x ) +c



(7.28)

where c



is a nonnegative constant. In Eq. (7.28), the last two deﬁnitions stem from the

ﬁrst one and the properties in Eqs. (7.26) and (7.27).

The above results represent various relations of algorithmic complexity between two

strings x, y. We immediately note that such relations bear a striking resemblance with

that concerning the joint or conditional entropies and mutual information of two random-

event sources X, Y according to classical IT.

See: G. J. Chaitin, A theory of program size formally identical to information theory. JACM, 22 (1975), 329–

40, www.cs.auckland.ac.nz/CDMTCS/chaitin/acm75.pdf. See also: G. J. Chaitin, Algorithmic information

theory. IBM J. Res. Dev., 21 (1977), 350–9, 496, www.cs.auckland.ac.nz/CDMTCS/chaitin/ibm.pdf.

From the ﬁrst deﬁnition in Eq. (7.26) we obtain K (y

x ) ≥ K (x) − K (x, y) −c, therefore, there exists a

constant c



≥ 0 for which K (y

x ) = K (x) − K (x, y) +c



7.5 Kolmogorov complexity vs. Shannon’s entropy 123

Indeed, to recall from Chapter 5, the conditional and joint entropies are related

through

H(X

Y ) = H (X, Y ) − H (Y ) (7.29)

and

H(Y

X ) = H (X, Y ) − H (X), (7.30)

which are deﬁnitions similar to those in Eqs. (7.26) and (7.27) for the conditional

complexity. From Chapter 5, we also have, for the mutual information,







H(x; y) = H(X ) + H (Y ) − H(X, Y )

H(x; y) = H(X ) − H (X

Y )

H(x; y) = H(Y ) − H(Y

X ),

(7.31)

which are deﬁnitions similar to that in Eq. (7.28) for the mutual complexity. It is

quite remarkable that the chaining relations of conditional or joint complexities and

conditional or joint entropies should be so similar (except in algorithmic IT for the

ﬁnite constant c



, which is nonzero in the general case), given the conceptual differences

between Kolmogorov complexity and Shannon entropy! As a matter of fact, such a

resemblance between algorithmic and classical IT is not at all fortuitous. As stated at

the beginning of this chapter, complexity and entropy are approximately equal when it

comes to random events or sequences: the average size of a minimal-length program

describing random events or sequences x from a source X is, indeed, approximately

equal to the source entropy, or K (x)

≈ H(X ). The conceptual convergence between

algorithmic entropy and Shannon entropy is formalized in the next section.

7.5 Kolmogorov complexity vs. Shannon’s entropy

As we have seen, complexity can be viewed as a measure of information, just like

Shannon’s entropy. The key difference is that complexity K (x) measures the information

from an individual event x, while entropy H (X ) measures the average information from

an event source X. Despite this important conceptual difference, I have shown in the

previous section the remarkable similarity existing between chain rules governing the

two information measures. In this section, I shall formally establish the actual (however

approximate) relation between Shannon’s entropy and Kolmogorov complexity.

Consider a source X of random events x

with associated probabilities p(x

). For

simplicity, we will ﬁrst assume that the source is binary, i.e., the only two possible

events are x

= 0orx

= 1, thus p(x

) = 1 − p(x

). We can record the succession

of n such events under the form of a binary string of length n, which we deﬁne as

x = x

(1)

(2)

(3)

...x

(n)

with i = 1, 2.

124 Algorithmic entropy and Kolmogorov complexity

We can then estimate the upper bound of the conditional complexity of K (x

n )

according to Eq. (7.21), which I repeat here with the new notations:

K (x

n ) ≤ 2logn + nf







j=1

( j)





+ c, (7.32)

where (to recall) f (u) =−u log

u − (1 −u)log

(1 − u).

Next, we take the expectation value

of both sides in Eq. (7.32) to obtain:



K (x

n )



≤

2logn + nf







j=1

( j)





+ c

= 2logn + c +n







j=1

( j)





≤ 2logn + c +nf







j=1

( j)





(7.33)

= 2logn + c +nf

(

)

≡ 2logn + c +nH(X ).

To get the above result, we have made use of three properties.

First, we have applied Jensen’s inequality, which states that for any concave

function

F,wehave



F(u)



≤ F(





);

Second, we made the substitution x

( j)

=





= x

p(x

) + x

p(x

) ≡ q;

Third, we have used the property F

(

)

= H (X), which is the deﬁnition of the entropy

of a binary, random-event source X,seeEq.(4.13).

In the limit of large n, the result in Eq. (7.33) yields:



K (x

n )



≤

2logn

+ H (X) ≈ H (X ). (7.34)

This result means that for strings of sufﬁciently long length n, the average “per bit”

complexity



K (x

n )



/n has the source entropy H(X ) as an upper bound. This can

be equivalently stated: the average complexity of a random bit string,



K (x

n )



, is

upper-bounded by the entropy n H (X) of the source that generates it. Note that the same

conclusion is reached concerning nonbinary sources having M-ary symbols.

Since all events are independent, the probability of obtaining the string x = x

(1)

(2)

(3)

...x

(n)

is p(x) =

j=1

p(x

( j)

). The expectation value



K (x )



thus means



p(x)K (x), or the statistical average over all

possibilities of strings x.

Jensen’s inequality applies to concave functions, which have the property that they always lie below any

chord (such as

√

x, −x

,orlog(x )).

T. M. Cover and J. A. Thomas, Elements of information theory (New York: John Wiley & Sons, 1991).

7.6 Exercises 125

Next, we try to ﬁnd a lower bound to



K (x

n )



/n. To each string x corresponds a

minimal-length program q, which is able to output x from a universal Turing machine U ,

i.e., U (q, n) = x. It will be shown in Chapter 8 that the average length L =l(q)of such

programs cannot exceed the source entropy, nH(X). Equivalently stated, the source’s

entropy is a lower bound of the mean program length, i.e., nH(X ) ≤ L.Itisalso

shown there that if the program length for each q is chosen such that l(q) =−log p(x),

then the equality stands, i.e., L = nH(X). Here, I shall conveniently use this property

to complete the demonstration. As we know, the conditional complexity K (x

n )is

precisely the shortest program length that can compute x.Thus,wehave



K (x

n )





l(q)



= L ≥ nH(X ), and

H(X ) ≤



K (x

n )



. (7.35)

Combining the results in Eqs. (7.34) and (7.35), we obtain the double inequality

H(X ) ≤



K (x

n )



≤

2logn

+ H (X). (7.36)

It is seen from the ﬁnal result in Eq. (7.36) that as the string length n increases, the

two boundaries converge to H(X ), and thus the per-bit complexity



K (x

n )



/n and the

source entropy H (X ) become identical. For the purpose of the demonstration, we needed

to consider “bits” and “strings.” But we could also consider X

∗

as a random source of

strings x with probability p(x) and entropy H(X

∗

). Thus, we have



K (x)



≈ H (X

∗

)as

the asymptotic limit, which eliminates the need to refer to a “per-bit” average complexity.

The above result, thus, establishes the truly amazing and quite elegant property

according to which Kolmogorov complexity and Shannon’s entropy give very similar

measures of information. Such an asymptotic relationship holds despite the profound

conceptual difference existing between algorithmic and Shannon information theories.

7.6 Exercises

7.1 (M): Use a Turing machine to add the two numbers i = 4 and j = 2, using the

action table in Table 7.3.

7.2 (B): Use a Turing machine to subtract the two numbers i = 4 and j = 3, using the

action table in Table 7.5.

7.3 (T): Solve Exercise 7.2 ﬁrst. Then complete the subtraction algorithm by introduc-

ing a new TM state aiming to clean up the useless 0 in the output tape sequence,

in the general case with i ≥ j.

7.4 (T): Deﬁne, for a Turing machine, an algorithm Comp, and a corresponding action

table, whose task is to compare two integers i, j, and whose output is either

Comp(i ≥ j) = 0orComp(i < j) = 1. Clue: begin the analysis by solving Exer-

cise 7.2 ﬁrst.

126 Algorithmic entropy and Kolmogorov complexity

7.5 (T): Determine the number of division or subtraction operations required to convert

the unary number

= 11 1111 1111 1111 0

into its decimal (N

) representation. Notes: (a) separators _ have been introduced

in the deﬁnition of N

for the sake of reading clarity; (b) the convention of the

unary representation chosen here is 1

= 10.

7.6 (T): Show how a Turing machine can convert the binary number

= 1001

into its unary (M

) representation. Note: use the convention for the unary repre-

sentation 1

= 10.