Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

8.6 Shannon’s source-coding theorem 147

Table 8.5 (

cont

Quaternary coding 26-ary coding

Ideal Real Mean Ideal Real Mean

CW CW CW CW CW CW

length length length length length length

xp(x ) p log

(p) l

∗

(x ) l

∗∗

(x ) l

∗∗

(x )p(x) p log

(x ) l

∗

(x ) l

∗∗

(x ) l

∗∗

(x )p(x)

O 0.075 0.140 1.8706 2 0.150 0.060 0.7959 1 0.075

I 0.070 0.134 1.9204 2 0.140 0.057 0.8171 1 0.070

N 0.067 0.130 1.952 2 0.134 0.055 0.8306 1 0.067

S 0.063 0.125 1.9964 2 0.126 0.053 0.8495 1 0.063

H 0.061 0.123 2.0197 3 0.182 0.052 0.8594 1 0.061

R 0.060 0.122 2.0316 3 0.179 0.052 0.8644 1 0.060

D 0.043 0.097 2.2719 3 0.129 0.041 0.9667 1 0.043

L 0.040 0.093 2.3241 3 0.120 0.039 0.9889 1 0.040

C 0.028 0.072 2.5814 3 0.084 0.031 1.0984 2 0.056

U 0.028 0.072 2.5814 3 0.084 0.031 1.0984 2 0.056

M 0.024 0.064 2.6926 3 0.072 0.027 1.1457 2 0.048

W 0.024 0.064 2.6926 3 0.072 0.027 1.1457 2 0.048

F 0.022 0.060 2.7553 3 0.066 0.026 1.1724 2 0.044

G 0.020 0.056 2.8241 3 0.060 0.024 1.2016 2 0.040

Y 0.020 0.056 2.8241 3 0.060 0.024 1.2016 2 0.040

P 0.019 0.054 2.8611 3 0.057 0.023 1.2174 2 0.038

B 0.015 0.045 3.0316 4 0.060 0.019 1.2899 2 0.030

V 0.010 0.033 3.3241 4 0.040 0.014 1.4144 2 0.020

K 0.008 0.028 3.4851 4 0.032 0.012 1.4829 2 0.016

J 0.002 0.009 4.4851 5 0.010 0.004 1.9084 2 0.004

X 0.002 0.009 4.4851 5 0.010 0.004 1.9084 2 0.004

Q 0.001 0.005 4.9851 5 0.005 0.002 2.1211 3 0.003

Z 0.001 0.005 4.9851 5 0.005 0.002 2.1211 3 0.003



1.000

Entropy H

= 2.092 L

∗∗

= 2.472 H

= 0.890 L

∗∗

= 1.226

quad/symbol quad/symbol 26-it/symbol 26-it/symbol

(source) (code) (source) (code)

Coding 84.63% 72.63%

efﬁciency

worse for any other M-ary codewords. This property

can easily be explained through

the deﬁnition of coding efﬁciency:

∗∗



x∈X

p(x)−log

x

To my knowledge, this is not found in any textbooks.

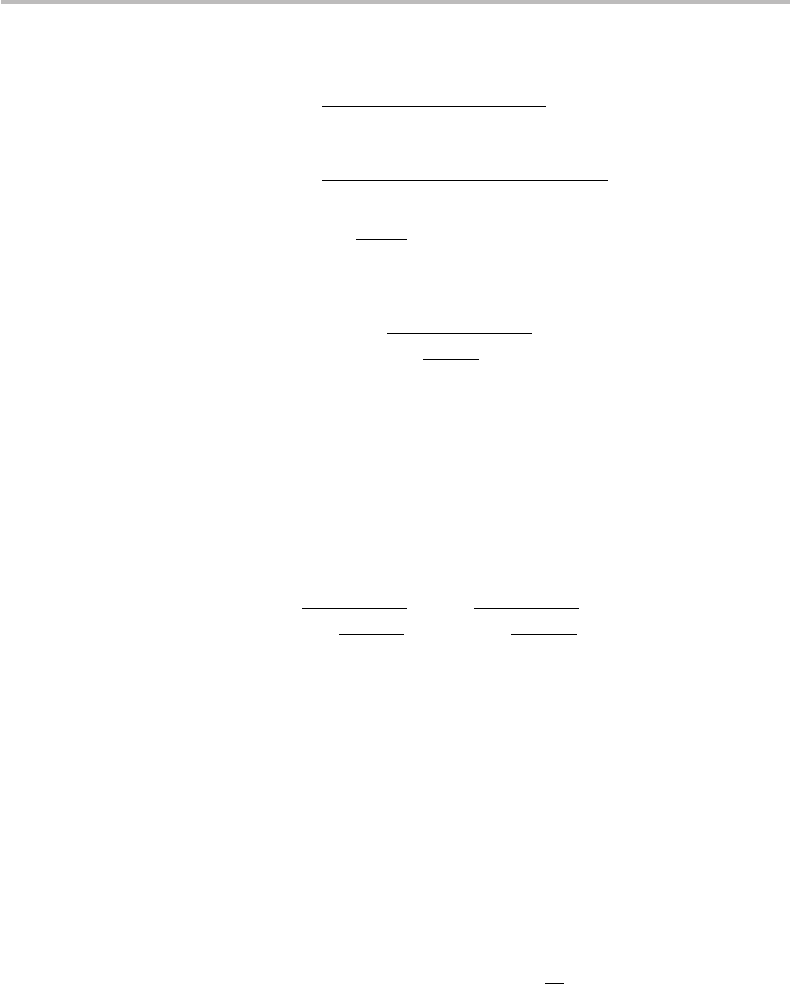
148 Information coding



x∈X

p(x)[−log

x + ε

(x)]

(8.18)

−



x∈X

p(x)log

x +



x∈X

p(x)ε

(x)

≡ 1 +

ε



which gives, using the relation H

ln M = H

ln 2,

η ≡

1 +

ln M

ln 2

ε



. (8.19)

It is seen that the coding efﬁciency decreases in inverse proportion to ln M, which for-

mally conﬁrms our previous numerical results. However, this decrease is also a function

of ε



, which represents the mean value of the truncations of −log

p(x). Both

depend on M and the distribution p(x), therefore, there is no general rule for estimating

it. We may, however, conservatively assume that for most probability distributions of

interest we should have 0.25 ≤ε



≤ 0.5, which is well satisﬁed in the example in

Table 8.5,

and which yields the coding efﬁciency boundaries:

1 +

ln M

ln 2

≤ η ≤

1 +

ln M

ln 2

. (8.20)

This last result conﬁrms that the efﬁciency of Shannon codes is highest for binary

codewords and decreases as the reciprocal of the number of alphabet characters used for

the codewords (ln M/ ln 2).

I will show next that the Shannon code is generally optimal when considering individ-

ual (and not average) codeword lengths, which we have noted l

∗∗

(x). Consider, indeed,

any different code for which the individual codeword length is l(x). A ﬁrst theorem states

that the probability P for which l

∗∗

(x) ≥ l(x) + n (n = number of excess bits between

the two codes) satisﬁes P ≤ 1/2

n−1

Thus, the probability that the Shannon code

yields an individual codeword length in excess of two bits (or more) is 1/2 at maximum.

Using the property P(l

∗∗

≥ l) = 1 − P(l

∗∗

< l), we can express this theorem under the

alternative form:

[

∗∗

(x) < l(x) + n

]

≥ 1 −

, (8.21)

which shows that the probability of the complementary event (l

∗∗

< l + n) becomes

closer to unity as the number of excess bits n increases. Such a condition, however, is

not strong enough to guarantee with high probability that l

∗∗

(x) < l(x) in the majority

of cases and for any code associated with l(x).

The detailed calculation yields ε



≈ 0.39, ε



≈ 0.48, ε



≈ 0.38, ε



≈ 0.47, and ε



≈

0.33.

See T. M. Cover and J. A. Thomas, Elements of Information Theory (New York: John Wiley & Sons, 1991).

8.7 Exercises 149

A second theorem of Shannon codes yields an interesting and quite unexpected prop-

erty. It applies to probability distributions for which l

∗∗

= l

∗

, meaning that −log p(x)

is an integer for all x. As we have seen earlier, such a distribution is said to be

dyadic. This theorem states that for a dyadic source distribution (see proof in previous

note):

[

∗

(x) < l(x)

]

≥ P

[

∗

(x) > l(x)

]

, (8.22)

where (to recall) l

∗

(x) is the individual codeword length given by Shannon coding and

l(x) is that given by any other code. It is, therefore, always more likely for dyadic

sources that the Shannon code yields strictly shorter individual codeword lengths than

the opposite. This is indeed a stronger statement than in the previous case, concerning

nondyadic sources. It should be emphasized that these two theorems of Shannon-coding

optimality concern individual, and not mean codeword lengths. As we shall see in the

next chapter, there exist codes for which the mean codeword length is actually shorter

than that given by the Shannon code.

The different properties that I have established in this section provide a ﬁrst and

vivid illustration of the predictive power of information theory. It allows one to know

beforehand the expected minimal code sizes, regardless of the source type and the coding

technique (within the essential constraint that the code be a preﬁx one). This knowledge

makes it possible to estimate the efﬁciency of any coding algorithm out of an inﬁnite

number of possibilities, and how close the algorithm is to the ideal or optimal case. The

following chapter will take us one step further into the issue of coding optimality, which

stems from the introduction of Huffman codes.

8.7 Exercises

8.1 (B): Consider the source with the symbols, codewords and associated probabilities

showninTable8.6:

Table 8.6 Data for Exercise 8.1.

Symbol Codeword x Probability p(x)

A 1110 0.05

B 110 0.2

C 1111 0.05

D 0 0.4

E 10 0.3

Calculate the mean codeword length, the source entropy and the coding efﬁciency.

8.2 (M): Provide an example of a dyadic source for a dictionary of four binary code-

words, and illustrate Shannon’s source-coding theorem.

See T. M. Cover and J. A. Thomas, Elements of Information Theory (New York: John Wiley & Sons, 1991).

150 Information coding

8.3 (M): Assign a uniquely decodable code to the symbol-source distribution given in

Table 8.7.

Table 8.7 Data for Exercise 8.3.

Symbol x Probability p(x)

A 0.302

B 0.105

C 0.125

D 0.025

E 0.177

F 0.016

G 0.250



1.000

and determine the corresponding coding efﬁciency.

8.4 (M): Assign a Shannon–Fano code to the source deﬁned in Exercise 8.3, and deter-

mine the corresponding coding efﬁciency η = H (X )/L

∗∗

(X ) and code redundancy

∗∗

(X ) − H(X ).

9 Optimal coding and compression

The previous chapter introduced the concept of coding optimality, as based on variable-

length codewords. As we have learnt, an optimal code is one for which the mean

codeword length closely approaches or is equal to the source entropy. There exist several

families of codes that can be called optimal, as based on various types of algorithms.

This chapter, and the following, will provide an overview of this rich subject, which ﬁnds

many applications in communications, in particular in the domain of data compression.

In this chapter, I will introduce Huffman codes, and then I will describe how they can

be used to perform data compression to the limits predicted by Shannon. I will then

introduce the principle of block codes, which also enable data compression.

9.1 Huffman codes

As we have learnt earlier, variable-length codes are in the general case more efﬁcient

than ﬁxed-length ones. The most frequent source symbols are assigned the shortest

codewords, and the reverse for the less frequent ones. The coding-tree method makes it

possible to ﬁnd some heuristic codeword assignment, according to the above rule. Despite

the lack of further guidance, the result proved effective, considering that we obtained

η = 96.23% with a ternary coding of the English-character source (see Fig. 8.3,

Table 8.3). But we have no clue as to whether other coding trees with greater coding

efﬁciencies may ever exist, unless we try out all the possibilities, which is impractical.

The Huffman coding algorithm provides a near-ﬁnal answer to the above code-

optimality issue. The coding algorithm consists in four steps (here in binary imple-

mentation, which is easy to generalize to the M-ary case

(i) List the symbols in decreasing order of frequency/probability;

(ii) Attribute a 0 and a 1 bit to the last two symbols of the list;

(iii) Add up their probabilities, make of the pair a single symbol, and reorder the list (in

the event of equal probabilities, always move the pair to the highest position);

(iv) Restart from step one, until there is only one symbol pair left.

In ternary coding, for instance, the symbols must be grouped together by three; in quaternary coding, they

should be grouped by four, and so on. If there are not enough symbols to complete the M groups, dummy

symbols having zero probabilities can be introduced at the end of the list to complete the tree.

152 Optimal coding and compression

CodeProbabilitySymbol

0.50.50.5

0.50.30.2

0.20.2

0.1

000

001

Figure 9.1 Implementation of Huffman coding for the source x ={x

, x

} with associated

probability distribution p(x) = {0.5, 0.2, 0.2, 0.1}.

An example of Huffman-coding implementation is provided in Fig. 9.1. The source is

X ={x

, x

}, with respective probabilities p(x) ={0.5, 0.2, 0.2, 0.1}. The ﬁgure

shows how the above-described pairs are formed and their probability sums replaced in

the next list. We see that the last two symbols (x

, x

) represent a probability of 0.3,

which comes in second position, after x

and before x

. Then the pair [x

, (x

, x

)]

represents the same probability as x

, but we place it on top of the next list, according to

the above rule. The groundwork is now complete. The code assignment simply consists

in following the arrows and writing down the 0 or 1 bits encountered in the path. The

codeword is the same word but with the bits written in the reverse order. For instance, we

ﬁnd for x

the bit path 100, so the codeword is 001. For x

, we ﬁnd 10, so the codeword

is 01, and so on.

How efﬁcient is Huffman coding? It is easy to calculate that in the above example, the

mean codeword length L is 1.80 bit/word. The entropy H is 1.76 bit/symbol. The coding

efﬁciency is, therefore, η = 1.76/1.8 = 97.8%, which is nearly ideal. For comparison,

if we had attributed to each of the symbols the same codeword length of two bits, we

would have L = 2 and η = 1.76/2 = 88%. If we used the Shannon–Fano code, it is

easily veriﬁed that the mean length L

∗∗

is 2.1 bit/word, and the efﬁciency drops to

η = 1.76/2.1 = 83%.

To become further convinced of the merits of Huffman coding, consider again the

English-character source, for which we have already explored several coding possibilities

(namely, 5-bit ASCII, Morse, and Shannon–Fano). It is a patient exercise (although not

without fun, as the reader should experience) to proceed by hand through the successive

steps of the Huffman algorithm on a large piece of paper or a blackboard.

The results

are shown in Table 9.1 (codeword assignment) and Fig. 9.2 (coding tree). As the table

shows, the minimum codeword length is three bits (two symbols) and the maximum

is nine bits (four symbols). The mean codeword length is 4.212 bit/symbol, yielding

a remarkably high efﬁciency of η = 4.184/4.212 = 99.33%. A comparison between

Table 9.1 (Huffman code) and Table 8.5 (Shannon code, binary) only reveals apparently

small differences in codeword length assignments. The remarkable feature is that such

apparently small differences actually make it possible to increase the coding efﬁciency

from 91.42% (Shannon code) to 99.33% (Huffman code).

A recommended class project is to write a computer program aiming to perform a Huffman-coding assign-

ment, with team competition for the fastest and most compact algorithm, while taking sources with a large

number of symbols for test examples.

9.1 Huffman codes 153

Table 9.1 Binary Huffman code for English-letter source, showing assigned codeword and calculation of mean

codeword length, leading to a coding efﬁciency of η = 99.33%. The two columns at far right show the new

probability distribution q(x) =−log(2

−l(x)

) and the Kullback–Leibler distance D( pq).

Length

xp(x) −p(x)log

(x) Codeword l(x) p(x)l(x) q(x) D(pq)

E 0.127 0.378 011 3 0.380 0.125 0.002

T 0.091 0.314 111 3 0.272 0.125 −0.042

A 0.082 0.295 0001 4 0.327 0.063 0.032

O 0.075 0.280 0010 4 0.299 0.063 0.019

I 0.070 0.268 0100 4 0.279 0.063 0.011

N 0.067 0.261 0101 4 0.267 0.063 0.006

S 0.063 0.251 1000 4 0.251 0.063 0.000

H 0.061 0.246 1001 4 0.243 0.063 −0.002

R 0.060 0.243 1010 4 0.239 0.063 −0.004

D 0.043 0.195 00000 5 0.214 0.031 0.020

L 0.040 0.185 00110 5 0.199 0.031 0.014

C 0.028 0.144 10110 5 0.140 0.031 −0.005

U 0.028 0.144 10111 5 0.140 0.031 −0.005

M 0.024 0.129 11001 5 0.120 0.031 −0.009

W 0.024 0.129 11010 5 0.120 0.031 −0.009

F 0.022 0.121 11011 5 0.110 0.031 −0.011

G 0.020 0.113 000010 6 0.120 0.016 0.007

Y 0.020 0.113 000011 6 0.120 0.016 0.007

P 0.019 0.108 001110 6 0.114 0.016 0.005

B 0.015 0.091 001111 6 0.090 0.016 −0.001

V 0.010 0.066 110001 6 0.060 0.016 −0.006

K 0.008 0.056 1100000 7 0.056 0.008 0.000

J 0.002 0.018 110000100 9 0.018 0.002 0.000

X 0.002 0.018 110000101 9 0.018 0.002 0.000

Q 0.001 0.010 110000110 9 0.009 0.002 −0.001

Z 0.001 0.010 110000111 9 0.009 0.002 −0.001



1.000 1.000

Source entropy

4.184

bit/symbol

Coding

efﬁciency η

99.33%

Mean codeword

length L

4.212

KL distance 0.028

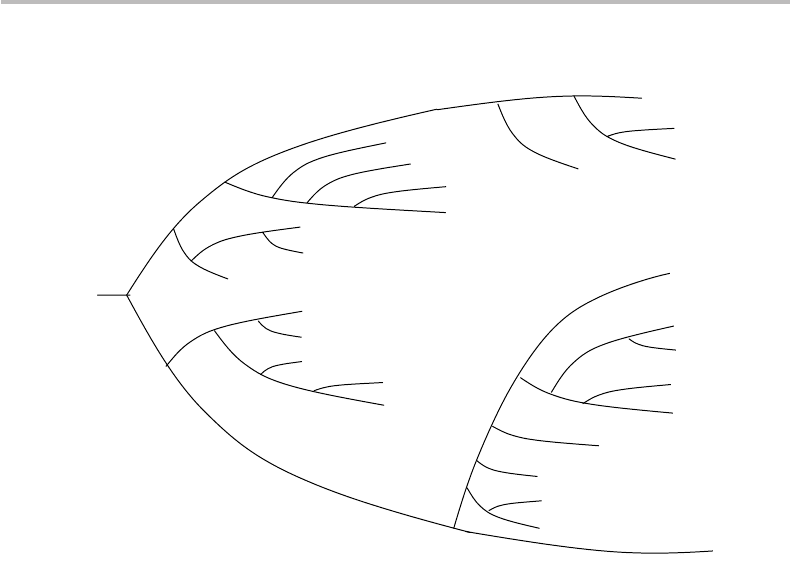
Looking next at Fig. 9.2, the coding tree is seen to be of order nine, meaning that

there are nine branch splits from the root, corresponding to the maximum codeword size.

A complete tree of order 9 has 2

= 512 terminal nodes, and 2

− 1 = 1023 nodes in

total. Our coding tree, thus, represents a trimmed version of the complete order-9 tree.

One says that the ﬁrst is “embedded” into the second. Note that the symbol/codeword

assignment we have derived here is not unique. For instance, the codewords of letters E

and T can be swapped, and any codeword of length l can be swapped within the group of

154 Optimal coding and compression

0100 I

0101 N

011 E

0010 O

00110 L

001110 P

001111 B

0001 A

00000 D

000010 G

000011 Y

1000 S

1001 H

1010 R

10110 C

10111 U

111 T

11010 W

11011 F

11001 M

110001 V

110000111 Z

1100000 K

110000110 Q

110000101 X

110000100 J

Figure 9.2 Coding tree for A–Z English-character source and binary codeword assignment (see

also Table 8.5). The convention is that branches pointing upwards are labeled 0 and branches

pointing downwards are labeled 1.

m symbols assigned the same length (representing m! possible substitutions, for instance

7! = 5040 for symbol groups numbering m = 7). Additionally, all bits can be logically

inverted, which generates a duplicated set of codewords.

From the coding tree in Fig. 9.2, one calculates that the number of possible sym-

bol/codeword assignments yielding the same coding efﬁciency is, in fact:

N = 2 ×(2! ×7! ×7! ×5! ×1! ×4!) = 292 626 432 000 = 2.92 10

, (9.1)

which represents no less than some 300 billion possibilities!

The two previous examples illustrate that Huffman coding is an optimal code that

brings coding efﬁciency relatively close to the 100% limit. However, such a conclu-

sion appears to be in contradiction with a key result obtained in Chapter 8 concern-

ing the Shannon–Fano code. Indeed, we have seen that any codeword-length assign-

ment

l(x) =−log q(x) that is different from that of the Shannon–Fano code, namely,

∗∗

(x) =−log p(x), results in a “penalty” for the mean codeword length,

L(X ). Such

a penalty is equal to the Kullback–Leibler (KL) distance D ≡ D(pq), or, after Eq.

(8.17),

L(X ) ∈ [H

(X ) + D, H

(x) + D + 1]. Yet, we should not conclude from this

result that

L(X ) > L

∗∗

(X ). As a matter of fact, the situation is exactly opposite for our

English-letter coding example. Indeed, we ﬁnd from Table 9.1 that D( pq) = 0.028

(and, incidentally, ε

≡ 0 since q(x)isoftheform2

−m

). Referring to the results in

9.1 Huffman codes 155

both Table 8.5 and Table 9.1, we obtain from Eq. (8.15) and Eq. (8.17):

∗∗

(X ) = 4.577 ∈ [4.184, 4.184 +1] ≡ [4.184, 5.184]

L(X ) = 4.212 ∈ [4.184 +0.028, 4.184 +0.028 +1] ≡ [4.212, 5.212],

which shows not only that the Huffman code is more efﬁcient (or closer to optimal) than

the Shannon code (

L(X ) < L

∗∗

(X )) but also that in this example the penalty D(pq)

is very close to the difference  =

L(X ) − H

(X ). Incidentally, it appears here that

 = 0, but this is only an effect of number accuracy.

How does the Huffman code perform with dyadic sources? It is easy to establish from

any basic example with source p(x) = 2

−n(x)

(n(x) = integer) that, in such a case, the

Huffman-code algorithm assigns the individual codeword length l

∗

(x) =−log 2

−n(x)

n(x). This is the same result as for the Shannon–Fano code and, as we have seen earlier,

the resulting mean length is the absolute minimum, or

L(X ) = L

∗∗

(X ) ≡ H(X ). It is a

nice exercise to prove directly the general property according to which Huffman coding

of dyadic sources is 100% efﬁcient.

The important lesson and general conclusion to retain from the above analysis is that

the mean codeword length of Huffman codes

L(X ) is the smallest achievable, regardless

of the source distribution. One can also state that Huffman coding is optimal with respect

to any other code, meaning that the latter always yields longer or equal codeword lengths.

Such a property of optimality can be stated as follows:

If L(X) is the mean codeword length of any code different from the Huffman code, then

L(X) ≥

L(X).

The reader may refer to most IT textbooks for a formal proof of Huffman codes

optimality. As we have seen in Chapter 8, however, the individual codeword lengths,

∗

(x) ≡−log p(x)assigned by the Shannon–Fano code are generally shorter than that

provided by any other codes, including Huffman codes. Formally, this property can be

written under the form

∗

(x) ≤

l(x), most often

∗∗

(X ) ≥

L(x), always. (9.2)

The secondary conclusion is that for individual codeword lengths, the Shannon code is

optimal in most cases, while for mean codeword lengths, the Huffman code is optimal in

all cases.

This represents a most important property for data compression applications,

to be described in the next section.

As we have seen earlier, the redundancy bound of Shannon–Fano codes is ρ

bound

= 1,

meaning that in the general case, ρ = L

∗∗

− H < 1. It can be shown that for Huffman

codes,

the redundancy bound is ρ

bound

= p

min

+ log

[(2 log

e)/e] ≈ p

min

+ 0.08607,

The detailed calculation to ﬁve decimal places shows that H

(X ) = 4.18396, L(X ) = 4.21236, D( pq) =

0.02840, and  = 0.05680, which represents a small nonzero difference.

Note that the English-letter example (see Tables 8.5 and 9.1) corresponds to the case where the Huffman

code is also optimal for individual codeword lengths.

See: D. J. C. MacKay, Information Theory, Inference and Learning Algorithms (Cambridge, UK: Cambridge

University Press, 2003).

156 Optimal coding and compression

where p

min

is the smallest source-symbol probability. The Huffman coding efﬁciency,

η = H/

L, is, thus, guaranteed to be strictly greater than 1 −ρ/

L. In the example of

Table 9.1, for instance, we ﬁnd

L − H = 4.212 – 4.184 = 0.028, which is lower than

bound

= p

min

+ 0.08607 ≡ 0.001 + 0.08607 = 0.0877, and η = 99.33%, which is

greater than 1 −0.0877/4.212 = 97.9%. Even tighter redundancy bounds can also be

found for speciﬁc probability distributions.

9.2 Data compression

Any information source, such as texts, messages, recordings, data ﬁles, voice or music

recordings, still or motion pictures, can be coded into sequences of binary codewords. As

we have learnt, the encoding conversion can use either ﬁxed-length or variable-length

codes. In the ﬁrst case, the bit size of the resulting sequence length is a multiple of

the codeword length. In the second case, the sequence can be made shorter through an

adequate choice of code, or through a second coding conversion, from a ﬁrst ﬁxed-length

code to a better, variable-length code. Converting a binary codeword sequence into a

shorter one is called data compression.

Since the advent of the Internet and electronic mail, we know from direct personal

experience what data compression means: if compression is not used, it may seem to take

forever to upload or download ﬁles like text, slides, or pictures. Put simply, compression

is the art of packing a maximum of data into a smallest number of bits. It can be

achieved by the proper and optimal choice of variable-length codes. As we have learnt,

Shannon–Fano and Huffman codes are both optimal, since, in the general case, their

mean codeword length is shorter than the ﬁxed-length value given by L = log

N (N =

number of source symbols to encode).

The compression rate is deﬁned by taking a ﬁxed-length code as a reference, for

instance the ASCII code with its 7 bit/symbol codewords. If, with a given symbol source,

a variable-length code yields a shorter mean codeword length L < 7, the compression

rate is deﬁned as r = 1 − L/7. The compression rate should not be confused with coding

efﬁciency. The latter measures how close the mean codeword length is to the source

entropy, which we know to be the ultimate lower bound. This observation intuitively

suggests that efﬁcient codes do not lend themselves to efﬁcient compression. Yet, this

correct conclusion does not mean that further compression towards the limits given by

the source entropy is impossible, as we will see in the last section in this chapter, which

is concerned with block coding.

The previous examples with the A–Z English-character source shown in Table 8.5

(Shannon–Fano coding) and Table 9.1 (Huffman coding) represent good illustrations

of the data compression concept. Here, we shall take as a comparative reference the

codeword length of ﬁve bits used by ASCII to designate the restricted set of lower case

or upper case letters. With the results from the two aforementioned examples, namely

See: R. G. Gallager, Variations on a theme by Huffman. IEEE Trans. Inform. Theory, 24 (1978), 668–74.