Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

9.3 Block codes 167

100

150

200

250

300

350

HE AN IN ER RE ON ES EA TI AT ST EN AR ND OR TO NT ED IS

Frequency

Digram

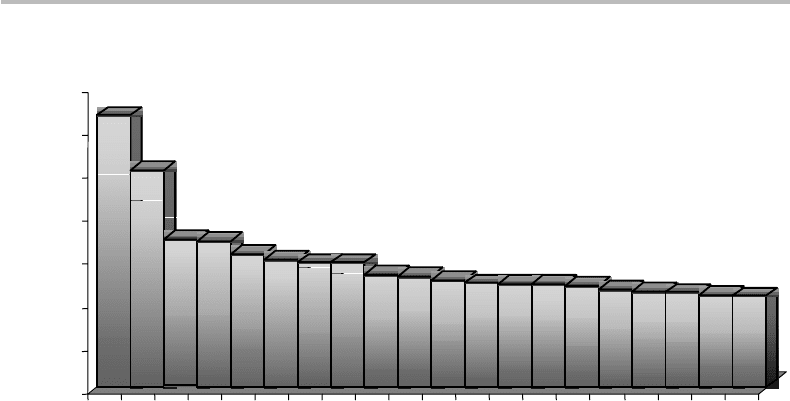
Figure 9.6 Arranging the leading English-letter digrams in order of decreasing frequency out of

a 10 000-letter count. The corresponding probability distribution is obtained by normalizing this

histogram by 10 000 (from data in Fig. 9.5 with c(y|x) ≥ 100).

into single characters, calling them, for instance,

T ,

H,or

A, respectively.

Ancient

scriptures include lots of such symbolic digram contractions, also called ligatures, which

helped the early writers, sculptors, or printers to produce their works more effectively or

artistically.

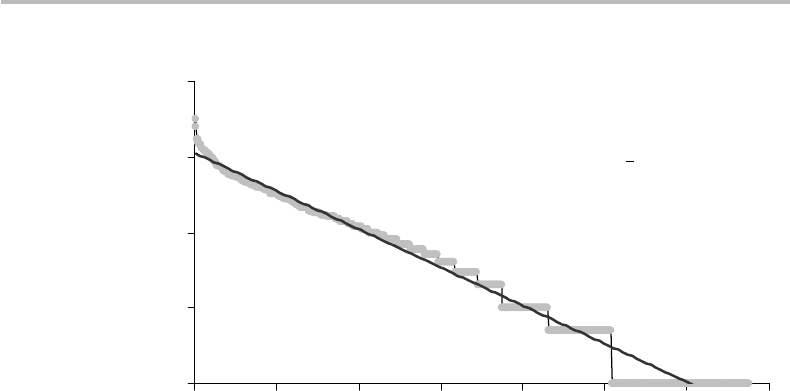
Figure 9.7 shows a logarithmic-scale plot of the 676 digrams in decreas-

ing order of frequency. The distribution is seen to be very nearly exponential, as the

numerical ﬁt indicates. The digram counts that were found to be zero in the reference

were changed to 0.5 and 0.1, to allow and to optimize this exponential ﬁt. The fact that

the distribution is exponential suggests that Shannon–Fano coding should be a good

approximation of an optimal (Huffman) code, considering the relatively large size of the

source.

The digram-source entropy is calculated to be H (X

(2)

) = 7.748 bit/digram. Interest-

ingly, it is smaller than H



= 2 × H (X

(1)

) =8.368, where H (X

(1)

) =4.185 bit/character

is the entropy of the English-language source. This fact is a positive indication that the

These are not to be confused with phonetics, which uses other super-alphabet codes in an attempt to emulate

and classify foreign-language sounds and vocal spelling.

A surviving contemporary example of digram ligatures is the symbol character &, called amper-

sand (or esperluette in French). It is in all computer keyboards, and is now used internationally as

the word contraction of “and”; see for reference: http://en.wikipedia.org/wiki/Ligature_(typography),

www.adobe.fr/type/topics/theampersand.html. The graphics of the ampersand character actually come from

the Latin word et. While the French use the same word as Latin, et, the Italian and Spanish use the shorter

words e and y, respectively, which do not call for symbol contraction, in contrast with most other languages.

A second example of a ligature, also in all computer keyboards, is the “at sign” character @, a contraction

for at, as used in e-mail addresses to indicate the domain name. Interestingly, its origins can be traced back

to the Middle Ages to designate weight or liquid capacity (in Spanish and Portuguese, amphora is arroba,

which yields the current French name of arobase). The character has also been commonly used in English

as a contraction of at to designate prices. See http://en.wikipedia.org/wiki/At_sign.

168 Optimal coding and compression

= 113.12e

0.0116

0.1

1.0

10.0

100.0

1000.0

7006005004003002001000

Digram

log

frequency

Figure 9.7 Plot of the 676 English-letter digram frequencies (logarithmic scale) out of a

10 000-letter count, showing that the distribution is very nearly exponential (from data in

Fig. 9.5).

English digrams contain less information, or uncertainty, than the mere concatenation

of letters by pairs. For the probability distribution, this implies that p(xy) ≥ p(x) p(y),

most generally for any symbol pair x, y, meaning that English letters are most often cor-

related to a certain extent, and correlation means less information. For instance, we ﬁnd

for the ﬁrst four leading digrams (xy = TH, HE, AN, IN) in Fig. 9.6 (dividing counts

by 10 000), the following probabilities:

p(TH) = 0.0313 > p(T)p(H) = 0.0055,

p(HE) = 0.0249 > p(H)p(E) = 0.0077,

p(AN) = 0.0171 > p(A)p(N) = 0.0054,

p(IN) = 0.0168 > p(I)p(N) = 0.0055,

which indeed illustrates a strong correlation attached to the four digrams TH, HE, AN,

and IN.

We shall consider next the coding of English digrams through binary codewords. This

will provide a good test for comparing the efﬁciencies of Shannon–Fano and Huffman

codes.

Owing to the size of the source, the calculation of the Huffman coding-tree must be

performed with a computer.

From my own computer program and test runs I found

that the Shannon–Fano and Huffman codeword lengths for the English-digram source

vary from l = 5tol = 17 (but obviously with different assignments), leading to the

Different algorithms and source programs can be found in the Internet, see for instance,

www.compressconsult.com/huffman/#codelengths and www.cs.mu.oz.au/∼alistair/inplace.c.

9.3 Block codes 169

following results:

Shannon–Fano code: L

∗∗

= 8.262 bit/digram η = 93.78%,

Huffman code:

L = 7.778 bit/digram η = 99.617%,

where for the source entropy the reference used is H = 7.748 bit/digram.

As expected, the Huffman code is found to be more efﬁcient than the Shannon–

Fano code. It is close to 0.3% of the source entropy, which represents a record value

for the examples described so far in these chapters! For comparison, we found ear-

lier (Table 9.1) that the efﬁciency of the English monograms is η = 99.33% (L

∗∗

4.212 bit/monogram), which is close to 0.6% of the source entropy. The efﬁciency of

monogram coding is, therefore, not signiﬁcantly different from that of digram coding.

Were we to compress an English book with Huffman codes, while assuming ﬁve bits per

character in the original book, we would get the following compression rates:

r = 1 −

= 1 −

4.212

= 15.76% (monogram code),

r = 1 −

= 1 −

8.262

= 17.38% (digram code).

The above ﬁgures are, in fact, quite conservative, because we took ﬁve-bit coding for

arbitrary reference. As we know, uncompressed texts use seven-bit ASCII. Overlooking

capitals, punctuation, and numbers (these being less frequent than lower-case letters),

and neglecting spaces, we can make a rough estimate of the compression rates with

respect to ASCII, as follows:

r = 1 −

= 1 −

4.212

= 39.82% (monogram code),

r = 1 −

= 1 −

8.262

= 40.98% (digram code),

which are the values typically found in standard data-compression software based on

Huffman coding.

The ﬁrst lesson learnt from this whole exercise is that block-coding makes it possible to

improve the compression rate. In the case of English, however, the improvement from

using digram blocks instead of monogram characters is not very signiﬁcant. Note that

the performance could be further improved by using longer blocks (trigrams, quadri-

grams, etc.), but at the expense of manipulating enormous dictionaries with codewords

having relatively long average lengths. The second lesson is that block codes also make

it possible to increase the coding efﬁciency when the events in the original source exhibit

a fair amount of mutual correlation, as we have seen with English digrams. However,

we should not conclude that block codes are more efﬁcient with such sources, and are

less efﬁcient with sources of mutually uncorrelated events. The last example shall prove

this point.

See, for instance, www.ics.uci.edu/∼dan/pubs/DC-Sec4.html.

170 Optimal coding and compression

Example 9.3: Two-event source; the roulette game

We analyze the roulette game, as inspired by previous work,

but which is further

developed here. This game originated in France in the seventeenth century, and was

later imported to America with minor modiﬁcations, hence, the alternative expressions

of French wheel or American wheel. To recall, the principle of the roulette is to make

various types of bets on the ball landing at random in one of 36 spots, numbered from

1 to 36, of the rotating wheel. If the ball stops on the right spot number, the gain is

36 times the amount that was bet. To increase the odds on winning anything, bets can

also be made on one, two, or four numbers at once, but this reduces the gain in the

same proportion. To increase the variety of betting possibilities further, the wheel spots

are also divided into families: (a) numbers 1–18 and 18–36, (b) odd and even numbers,

A key feature of the roulette,

which is not friendly to the players, is the existence of an extra green number, called 0 in

the French wheel. The American wheel also has this number 0 plus a second one, called

00. When the ball lands on either 0 or 00, all bet proceeds go directly to the “bank.” It

is easy to establish that the odds on winning in the roulette game are relatively low, no

matter how hard one may try with any playing strategy.

Here, we shall simplify the game by assuming that the gambling exclusively concerns

a single number selected from 1 to 36. The corresponding probability of winning is

p (win) = p (no 0 or 00) ×p (number selected) =(1 −2/38) ×(1/36) =1/38 =0.0263,

and the probability of losing is p (lose) = 1 − p (win).

This is a two-event source

See B. Osgood, Mathematics of the Information Age (2004), p. 64, at www-ee.stanford.edu/∼osgood/

Sophomore%20College/Math%20of%20Info.htm.

See interactive example, while safely taking bets with “free money” at (for instance) www.mondo-

casinos.com/gratuit/roulette/index.php (note: this reference is for study purposes and does not constitute

in any way a recommendation of gambling).

If the roulette outcome is strictly random (can one always be sure of this?), the odds on the bank to pocket

all the bets with the 0 or 00 outcomes are 1/37 = 2.7% (French) and 2/38 = 5.4% (American). For the

individual player, the odds on winning any single-number bet are (1 −1/37)/36 =1/36 =2.7% (French) and

(1 −2/38)/36 =1/38 =2.6%. This means that (with respect to this player) the bank wins with probabilities

97.3% (French) and 97.4% (American). The odds on winning are obviously greater with the other bets

(a)–(c), namely (1 − 1/37)/2 = 48.6% (French) and (1 − 2/38)/2 = 47.3% (American) for (a)–(c) and

(1 − 1/37)/3 = 32.4% (French) and (1 − 2/38)/3 = 31.5% (American) for (d), but we note that they are

lower than 50% (a)–(c) or 33% (d), which, on average, is always in favor of the bank.

We note that in the real game, the odds on winning are less than 1/36, which makes the player’s situation

“unfair.” It is possible to play with a high probability of making zero gains, but this comes with a low

probability of making maximal loss. Indeed, if we place one token on each of the 36 numbers, two events

can happen:

(a) One of the 1–36 numbers comes out: we win 36 tokens, which is the exact amount we bet, and the net

gain is zero; this has a high probability of 36/38 = 94.75 % < 100%.

(b) The 0 or 00 comes out, the bank wins the 36 tokens (our loss is maximum); this has a low probability

of 2/38 = 5.25% > 0%.

Similar conclusions apply when tokens are placed in equal numbers in the “odd/even,” “red/black,” or

“1–12, 13–24, 25–36” ﬁelds. The ﬁrst lesson learnt is that even the least risky gambling options, which

have zero gain, most likely come with a small chance of maximal loss. Even in this extreme gambling

option, the game deﬁnitely remains favorable to the bank! Consider now the odds of winning if one plays

the same number 36 times in a row. The probability to lose all games is (1 −1/38)

= 38.3%, so there

9.3 Block codes 171

with entropy deﬁned by H (X) ≡ f (p) =−p log p − (1 − p)log(1− p), as described

in Chapter 4. Substituting p (win) in this deﬁnition yields H (X) = 0.17557 bit/symbol.

As we shall see later, we will need such a high accuracy to be able to analyze the code

performance.

Call the two source events W and L for the outcomes “win” and “lose.” A succession

of n roulette bets can, thus, be described by the sequence LLLLLWLL ..., which is

made of n symbols of the L/W type. As we have learnt so far in this chapter, it would

be a waste to represent such a sequence with an n-bit codeword. Rather, we should

seek for a variable-length codeword assignment, which uses the shortest codewords

for the most likely sequences, and the longest codewords for the least likely ones.

We should expect the mean codeword length to approach the extended source entropy

H(X

(n)

) = nH(X) ≡ 0.17557n = n/5.69, which is indeed signiﬁcantly shorter than n.

To ﬁnd such a code, we may proceed step by step, considering sequences with increasing

lengths, and determining a corresponding block code. We will compare the block code

efﬁciency with that of a Huffman code.

Consider ﬁrst a sequence of four games (n = 4). Overlooking the order of the indi-

vidual outcomes, there exist ﬁve types of possible sequences, in decreasing likelihood:

LLLL (complete loss), LLLW (one win), LLWW (two wins), LWWW (three wins), and

WWWW (four wins). We must then take into account the exact order of the individual

W/L associated to a given sequence type. For instance, the sequence types we called

LLLW and LWWW actually correspond to four possible unique outcomes:

LLLW, LLWL, LWLLL, WLLL;

LWWW, WLWW, WWLW, WWWL.

The sequence type LLWW is associated with six unique outcomes:

LLWW, LWLW, LWWL, WLWL, WWLL, WLLW,

while the sequences LLLL and WWWW have only one unique possibility. Most gener-

ally, the number of ways of selecting k slots from a sequence of n slotsisgivenbythe

combinatorial coefﬁcient C

(see Chapter 1):

k!(n − k)!

, (9.3)

which is also written





, and where q! = 1 ×2 ×3 ×···×(q − 1) ×q is called the

factorial of the integer q (by convention, 0! = 1). Consistently, we ﬁnd for LLLW or

LWWW the number C

= 4!/(1!3!) = 4, and for LLWW the number C

= 4!/(2!2!) =

6. Calling p the probability of winning a single game in the sequence, we can associate

is a 61.7% chance of winning one way or another, which looks a reasonable bet. But this number assumes

that we play 36 games, regardless of their outcome. The most likely possibility to win is that our number

comes once (and only once), which has the probability C

(1/38)

(1 −1/38)

=37.2%. In this event, we

win 36 tokens, but the price to pay is to lose 35 tokens for the other 35 games. The net result is that, with

61.7% chances and in the most favorable case, we have not gained anything at all! Furthermore, there are

38.3% chances that we lose 36 tokens. The second lesson learnt is the same as the ﬁrst lesson!

172 Optimal coding and compression

Table 9.4 Construction of variable-length block code for the American roulette, considering a succession of n = 4

independent games for which the outcome is lose (L) or win (W). The sequence LLLL (type A) corresponds to four wins,

the sequence LLLW (type B) to three losses and one win, and so on. Each sequence type has a probability p

and a

number of ordered possibilities N, yielding a net probability p = Np

. Each ordered possibility is labeled by a block

code made of a header and a trailer block. The header is coded with the uniquely decodable word of length HB,which

indicates the sequence type. The trailer ﬁeld has the minimum number of bits TB required to code N. The resulting

codeword length is M = HB + TB. At bottom are shown the total number of extended-source events, the mean

codeword length L =M, the extended-source entropy nH and the coding efﬁciency η = H/L .

N = 4games

No of

No of bits

trailer No of required,

Sequence Possibilities, bits, Probability, header M = HB

Type type Probability, p

NTBp= Np

Header bits, HB +TB Mp

A LLLL 0.89881955 1 0 0.89881955 1 1 1 0.89882

B LLLW 0.02429242 4 2 0.09716968 01 2 4 0.38868

C LLWW 0.00065655 6 3 0.00393931 001 3 6 0.02364

D LWWW 1.7745 ×10

−5

427.0979 × 10

−5

0001 4 6 0.00043

E WWWW 4.7959 ×10

−7

104.7959 × 10

−7

0000 4 4 0.00000



16 1.0000 ×10

L 1.31156

Extended source entropy nH = 0.70226.

Efﬁciency η = 53.544%.

each of the above sequence types with the corresponding probabilities:











p(LLLL) = C

(1 − p)

p(WWWW) = C

p(LLLW ) = C

p(1 − p)

p(WWWL) = C

(1 − p)

p(LLWW ) = C

(1 − p)

(9.4)

recalling that each of these types is associated with N = C

unique outcomes. Table 9.4

lists the data computed with p =1/38 =0.0263, the resulting probabilities being shown

in decreasing order, with the sequence types referred to as A, B, C, D, and E. To label

each of the sequence outcomes, we shall construct a variable-length block code made

with the concatenation of a header block with a trailer block. The header block is

coded with a uniquely decodable word of length HB, which indicates the sequence type

(A, B, C, D, or E). The trailer block has the minimum number of bits TB required

to code N . For instance, the outcome LLLL (type A) has the header 1 and an empty

trailer. The outcome LLLW (type B) has the header 01 and a trailer of two bits (namely

00, 01, 10, and 11) which labels each of the four unique possibilities in the type-B

sequence (namely LLLW, LLWL, LWLLL, and WLLL). The resulting codeword length

is, therefore, M = HB+ TB. Table 9.4 shows the mean codeword length L =M

and the coding efﬁciency η = nH/L, where nH is the entropy of the extended source

corresponding to the n independent outcomes of the n successive games. The results

9.3 Block codes 173

indicate that our block code takes L = 1.311 bit/word to describe any game sequence

uniquely, corresponding to a coding efﬁciency of η = 53.544%.

The efﬁciency of our block code (η = 53.544%) is not outstanding, indeed, but we

can measure the progress made by comparing it to that given by a ﬁxed-length code.

Indeed, if we use a four-bit codeword to describe any of the game sequences (e.g., 1010

for WLWL), the efﬁciency drops to η = 4H/4 = 0.1755 or 17.5%. The use of our

variable-length block code has, in fact, more than doubled the coding efﬁciency! With

respect to four-bit codewords, the compression rate obtained with the block code is r =

1 − 1.311/4 = 67.2%.

This ﬁrst example with sequences of n = 4 games illustrates that the efﬁciency of the

block code increases with the length of the sequence. Indeed, long sequences of events

contain more information than short sequences of events, because their associated prob-

abilities are lower.

Therefore, we can infer that our block coding becomes increasingly

efﬁcient with longer sequences, which we shall now verify. Table 9.5 shows the results

obtained with sequences of length n = 32. As the table ﬁrst shows, the number of events

is dramatically increased to a whopping 4 294 967 296 or about 4.3 billion possibilities!

The code is seen to have an average length of L = 5.771 bit/word, corresponding to

a coding efﬁciency of η = 97.34%. The corresponding compression rate is r = 1 −

5.771/32 = 81.9%.

The results obtained for n = 32 games seem to conﬁrm the previous observation,

according to which the code becomes increasingly efﬁcient with ever-longer sequences.

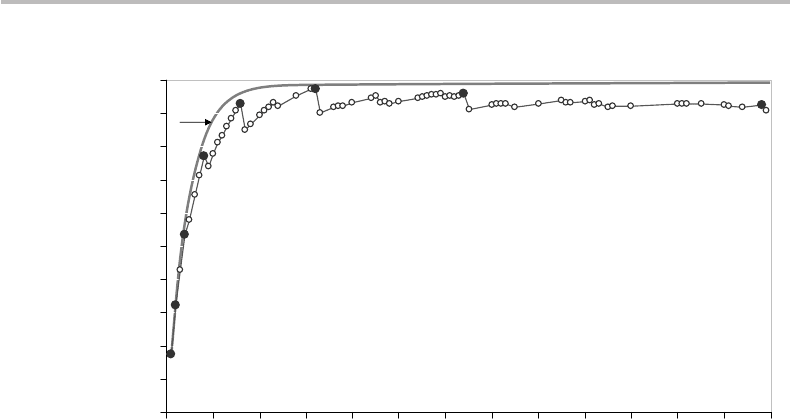
As it turns out, however, this is not the case! Figure 9.8 shows a plot of the coding

efﬁciency η, as computed with sequence lengths from n = 1ton = 129. From the

ﬁgure, we observe that the efﬁciency increase exhibits some irregularities, with local

peaks appearing whenever n is a power of two (n = 2

), but also for other intermediate

values. The irregularity observed between the peaks is explained by the fact that the

trailer bits, which label all outcome possibilities within a sequence type, are generally not

fully used. The use is optimal whenever n = 2

, which yields a local peak in efﬁciency.

Looking at Table 9.4 and Table 9.5, we observe indeed that it takes exactly two trailer bits

to describe the four possibilities of the sequence LLLW, and it takes exactly four trailer

bits to describe the 16 possibilities of the sequence LLLL LLLL LLLL LLLW. This

is not chance, since the number of possibilities is C

= n = 2

. Since these sequences

always come in second position in the distribution, this feature has a major impact

in reducing the mean codeword length. Other sequences with 2

< n < 2

k+1

require

an extra trailer bit, which explains the efﬁciency drops observed in Fig. 9.8 each time

where n = 2

+ 1(n ≥ 8). The ﬁgure also shows that, unexpectedly, the efﬁciency peaks

decrease past a maximum point obtained for n = 32. This effect can be attributed to the

fact that the number of possibilities C

(1 < q < n) grows exponentially with length.

Such a growth dramatically increases the number of codewords with inefﬁcient use

Isn’t this observation counterintuitive? We would, indeed, expect that there is more uncertainty (or entropy)

in shorter game series than in longer ones. But there is more information contained in the succession of

repeated events than in any single event taken separately.

It can easily be veriﬁed that for even values of n, the maximum of C

is reached at k = n/2. Using Stirling’s

formula, we obtain C

n/2

≈ 2

n+1

√

2πn.

Table 9.5 As for Table 9.4 but with n = 32.

No of No of No of bits

trailer header required,

bits, Probability, bits, M =

Case Events Probability, p

Possibilities, NTB p= Np

Header HB HB + TB Mp

A LLLL LLLL LLLL LLLL LLLL LLLL LLLL LLLL 0.425971044 1 0 0.42597104 1 1 1 0.425971044

B LLLL LLLL LLLL LLLL LLLL LLLL LLLL LLLW 0.011512731 32 5 0.36840739 01 2 7 2.578851726

C LLLL LLLL LLLL LLLL LLLL LLLL LLLL LLWW 0.000311155 496 9 0.15433283 001 3 12 1.851993904

D LLLL LLLL LLLL LLLL LLLL LLLL LLLL LWWW 8.40959 ×10

−6

4 960 13 0.04171157 0001 4 17 0.709096765

E LLLL LLLL LLLL LLLL LLLL LLLL LLLL WWWW 2.27286 ×10

−7

35 960 16 0.00817321 0000 1 5 21 0.171637492

F LLLL LLLL LLLL LLLL LLLL LLLL LLLW WWWW 6.14287 ×10

−9

201 376 18 0.00123703 0000 01 6 24 0.029688647

G LLLL LLLL LLLL LLLL LLLL LLLL LLWW WWWW 1.66024 ×10

−10

906 192 20 0.00015045 etc. 7 27 0.004062129

H LLLL LLLL LLLL LLLL LLLL LLLL LWWW WWWW 4.48712 ×10

−12

3 365 856 22 1.5103 ×10

−5

8 30 0.00045309

I LLLL LLLL LLLL LLLL LLLL LLLL WWWW WWWW 1.21274 ×10

−13

10 518 300 24 1.2756 ×10

−6

9 33 4.20945 ×10

−5

J LLLL LLLL LLLL LLLL LLLL LLLW WWWW WWWW 3.27766 ×10

−15

28 048 800 25 9.1935 ×10

−8

10 35 3.21771 ×10

−6

K LLLL LLLL LLLL LLLL LLLL LLWW WWWW WWWW 8.85855 ×10

−17

64 512 240 26 5.7149 ×10

−9

11 37 2.1145 ×10

−7

L LLLL LLLL LLLL LLLL LLLL LWWW WWWW WWWW 2.3942 ×10

−18

129 024 480 27 3.0891 ×10

−10

12 39 1.20475 ×10

−8

M LLLL LLLL LLLL LLLL LLLL WWWW WWWW WWWW 6.47082 ×10

−20

225 792 840 28 1.4611 ×10

−11

13 41 5.99037 ×10

−10

N LLLL LLLL LLLL LLLL LLLW WWWW WWWW WWWW 1.74887 ×10

−21

347 373 600 29 6.0751 ×10

−13

14 43 2.6123 ×10

−11

O LLLL LLLL LLLL LLLL LLWW WWWW WWWW WWWW 4.72668 ×10

−23

471 435 600 29 2.2283 ×10

−14

15 44 9.80463 ×10

−13

P LLLL LLLL LLLL LLLL LWWW WWWW WWWW WWWW 1.27748 ×10

−24

565 722 720 30 7.227 ×10

−16

16 46 3.32442 ×10

−14

Q LLLL LLLL LLLL LLLL WWWW WWWW WWWW WWWW 3.45265 ×10

−26

601 080 390 30 2.0753 ×10

−17

17 47 9.754 ×10

−16

R LLLL LLLL LLLL LLLW WWWW WWWW WWWW WWWW 9.33149 ×10

−28

565 722 720 30 5.279 ×10

−19

18 48 2.53394 ×10

−17

S LLLL LLLL LLLL LLWW WWWW WWWW WWWW WWWW 2.52202 ×10

−29

471 435 600 29 1.189 ×10

−20

19 48 5.70706 ×10

−19

T LLLL LLLL LLLL LWWW WWWW WWWW WWWW WWWW 6.81628 ×10

−31

347 373 600 29 2.3678 ×10

−22

20 49 1.16022 ×10

−20

U LLLL LLLL LLLL WWWW WWWW WWWW WWWW WWWW 1.84224 ×10

−32

225 792 840 28 4.1596 ×10

−24

21 49 2.03822 ×10

−22

V LLLL LLLL LLLW WWWW WWWW WWWW WWWW WWWW 4.97902 ×10

−34

129 024 480 27 6.4242 ×10

−26

22 49 3.14784 ×10

−24

W LLLL LLLL LLWW WWWW WWWW WWWW WWWW WWWW 1.34568 ×10

−35

64 512 240 26 8.6813 ×10

−28

23 49 4.25383 ×10

−26

X LLLL LLLL LWWW WWWW WWWW WWWW WWWW WWWW 3.63698 ×10

−37

28 048 800 25 1.0201 ×10

−29

24 49 4.99863 ×10

−28

Y LLLL LLLL WWWW WWWW WWWW WWWW WWWW WWWW 9.82966 ×10

−39

10 518 300 24 1.0339 ×10

−31

25 49 5.06618 ×10

−30

Z LLLL LLLW WWWW WWWW WWWW WWWW WWWW WWWW 2.65667 ×10

−40

3 365 856 22 8.942 ×10

−34

26 48 4.29214 ×10

−32

AA LLLL LLWW WWWW WWWW WWWW WWWW WWWW WWWW 7.18018 ×10

−42

906 192 20 6.5066 ×10

−36

27 47 3.05811 ×10

−34

AB LLLL LWWW WWWW WWWW WWWW WWWW WWWW WWWW 1.94059 ×10

−43

201 376 18 3.9079 ×10

−38

28 46 1.79762 ×10

−36

AC LLLL WWWW WWWW WWWW WWWW WWWW WWWW WWWW 5.24483 ×10

−45

35 960 16 1.886 ×10

−40

29 45 8.4719 ×10

−39

AD LLLW WWWW WWWW WWWW WWWW WWWW WWWW WWWW 1.41752 ×10

−46

4 960 13 7.0309 ×10

−43

30 43 3.02329 ×10

−41

AE LLWW WWWW WWWW WWWW WWWW WWWW WWWW WWWW 3.83114 ×10

−48

496 9 1.9002 ×10

−45

31 40 7.60099 ×10

−44

AF LWWW WWWW WWWW WWWW WWWW WWWW WWWW WWWW 1.03544 ×10

−49

32 5 3.3134 ×10

−48

32 37 1.22597 ×10

−46

AG WWWW WWWW WWWW WWWW WWWW WWWW WWWW WWWW 2.7985 ×10

−51

1 0 2.7985 ×10

−51

32 32 8.95519 ×10

−50



4 294 967 296 1.0000 ×10

L 5.771800335

Extended source entropy nH = 5.618081.

Efﬁciency η = 97.34%.

9.3 Block codes 175

100

130

120

110

100

Number of games

Coding efficiency (%)

= 1

= 2

= 4

= 8

= 16

= 32

= 64

= 128

= 9

Figure 9.8 Coding efﬁciency of variable-length block code describing a sequence of n roulette

game outcomes. The data corresponding to n = 2

(where k is an integer) are shown in dark. The

continuous curve corresponds to the envelope of ideal Huffman coding, as computed up to n = 9

and extrapolated beyond n = 9.

of trailer bits, which progressively reduces the maximum compression effect obtained

each time that n = 2

. Concerning the curve envelope (n = 9), which is also plotted in

Fig. 9.8, see further.

The above example illustrates that block coding can be quite efﬁcient and yield high

data compression, but care should be given to ﬁnd the optimum sequence length, if it

exists. A relevant question is: how does block coding compare with Huffman coding?

The second solution, which we know to be optimal in terms of compression power,

involves coding all events of the extended source X

(n)

through the coding-tree procedure

described earlier. If the number of extended-source events is reasonably small, the proce-

dure is easily and rapidly implemented. But it becomes impractical or prohibitive when

the number of source events grows exponentially with the block size n. In the case where

n = 16, for instance, the number of events is 2

= 4 294 967 296 or 4 billion. In the

case where n = 64, the number of events becomes 2

= 18 446 744 073 709 500 000,

or 18 billion billion! It does not make any sense to implement Huffman coding in

such a case. Yet, we have been able here to determine a block code and to calculate

its performance up to 2

129

= 6.8 × 10

= 680 ×10

× 10

. The explana-

tion is that the block-code assignment only takes the analysis of n + 1 block types, as

opposed to 2

individual events. With a home computer, we can easily compute Huff-

man codes up to a few thousand elements. What about Shannon–Fano coding? As we

know, the codeword assignment is straightforward in this case. As with block codes,

we do not have to consider the 2

events individually to compute the mean codeword

length.

176 Optimal coding and compression

987654321

Number of games

Efficiency (%)

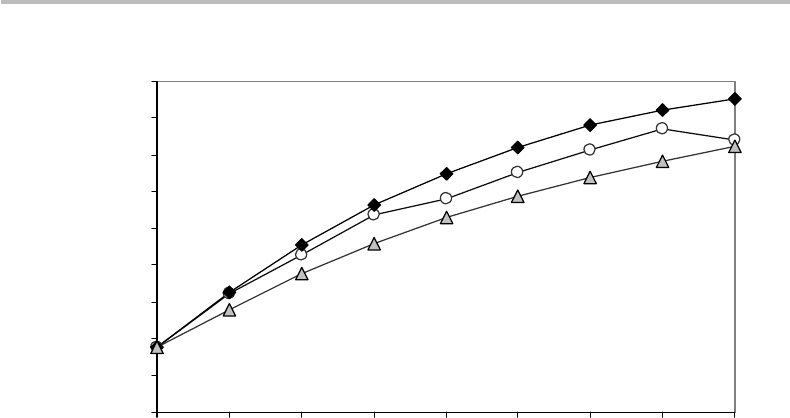
Figure 9.9 Comparison between Huffman coding (diamonds), block-coding (open circles), and

Shannon–Fano coding (triangles) in the roulette-game example of Fig. 9.8, with data calculated

up to n = 9.

The results for both Huffman coding and Shannon–Fano coding, as applied to the

roulette-game example, are shown in Fig. 9.9 for game sequence lengths n ≤ 9. We

observe from the ﬁgure that, as expected, the efﬁciency of the Huffman code is greater

than that of any other codes. Unlike the block code, both Huffman and Shannon–

Fano codes grow smoothly with the sequence length n. Interestingly, the block-code

performance is observed to be bounded by the two envelopes made by the Huffman

code (upper boundary) and the Shannon–Fano code (lower boundary). The Huffman-

code data in Fig. 9.9 have also been plotted in Fig. 9.8. In this previous ﬁgure, an

arbitrary, yet conservative extrapolation of what the Huffman-code performance should

look like for sequences beyond n = 9 is also shown. We expect that there is no optimal

sequence length, and know that the coding efﬁciency at n = 32 is greater than that

of our proposed block code (η = 97.34%). It would take the power of a workstation

or mainframe computer to determine the exact curve and ﬁnd the values of n for

which the Huffman-code efﬁciency approaches η = 99%, 99.9%, 99.99%, 99.999%,

etc.

The Shannon–Fano code efﬁciency, computed up to n = 90, is plotted in Fig. 9.10,

along with the previous data from Fig. 9.8. We observe that the initially smooth behavior

of the Shannon code breaks near N = 16, leading to aperiodic oscillations similar to

that of the block code. Interestingly, the efﬁciency of the Shannon–Fano code is seen

to increase globally towards the upper limit set by the Huffman code. As expected,

the Shannon–Fano code does not exhibit any optimum sequence length, apart from the

existence of local maxima.