Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

10.2 Arithmetic coding 187

Consider the basic example of a source X =

{

a, b, c

}

with probabilities p

) =

{

0.4, 0.4, 0.2

}

. We assume that symbol c is exclusively used to signal the end of message.

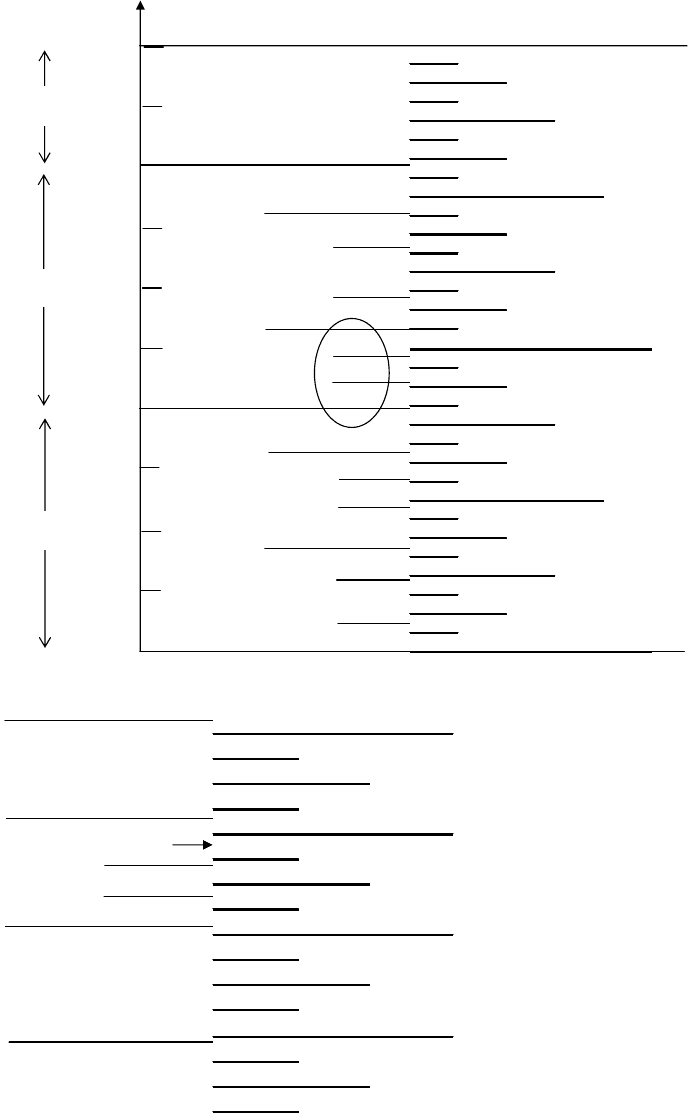
The interval containing all real values p such that 0 ≤ p < 1 is noted [0, 1). Our encoder’s

program then proceeds as follows (Fig. 10.1):

Step 1: The interval [0, 1) is ﬁrst divided into three subintervals [0.0, 0.4), [0.4, 0.8),

and [0.8, 1.0), corresponding to the symbol events a, b, and c, respectively. The interval

[0,1) is also divided into two equal regions, labeled in binary with preﬁxes 0 and 1,

as shown in the right-hand side. We observe from the ﬁgure that the preﬁx 1 so far

corresponds to either a or b, and the preﬁx 0 to either b or c.

Step 2: Each of the previous subintervals, except the last one [0.8, 1.0), corresponding

to event c, is divided into three subintervals, the widths of which correspond to

the joint probabilities p(x

, x

) = p(x

)p(x

) of either joint events aa, ab, ac,or

ba, bb, bc. The regions corresponding to labels 0 and 1 are also divided into two

equal parts, which are labeled with preﬁxes 00, 01, 10, and 11. We observe from the

ﬁgure that:

◦

The preﬁx 11 corresponds to either aa or ab;

◦

The preﬁx 10 corresponds to either ab, ac,orba;

◦

The preﬁx 01 corresponds to either ba, bb,orbc;

◦

The preﬁx 00 corresponds to either bc or c;

Step 3: Each of the previous subintervals, except the last ones corresponding to ﬁnal

events c, is divided again into three subintervals, the widths of which correspond to

the joint probabilities p(x

, x

) = p(x

, x

)p(x

) of joint events aaa, aab, aac,

aba, abb, abc, baa, bab, bac, bba, bbb, bbc. The region corresponding to preﬁxes

00, 01, 10, and 11 are also divided into two equal parts, which are labeled 000 to

111 and correspond to different joint-event possibilities, except for 000 which is

exclusively attached to event c.

The encoder is capable of executing the above steps an arbitrary number of times in

order to ﬁnd the preﬁx attached to a string of any length and ending in c. To clarify

this point, assume that the string (or joint event) to encode is bc. We observe from

Fig. 10.1(a) that the unique subinterval which is fully contained in the region deﬁned

by string bc has the preﬁx 00111. We can then use this preﬁx as the unique codeword

for string bc. The same observation applies, for instance, to the string aac, which

gets 11001 as a unique preﬁx and codeword. Assume next that the machine must

encode the string babc. The magniﬁcation in Fig. 10.1(b) shows that the subinterval

corresponding to preﬁx 1000001 is the only one to be fully contained in the region

deﬁned by string babc, and, therefore, it should be used as the unique codeword. In

summary, the encoder assigns a unique codeword to any symbol string (or joint event)

,...,x

c by slicing down the interval [0, 1) into as many subintervals of widths

p(x

, x

,...,x

, c) = p(c|x

, x

,...,x

)p(c). The algorithm to perform this operation

is described in detail in Appendix H. Our description represents a simpliﬁcation of the

more general algorithm described in MacKay (2003).

D. J. C. MacKay, A Short Course in Information Theory (Cambridge, UK: Cambridge University Press,

2003).

1.0

0.0

0.8

0.4

[0.8, 1.0)

[0.4, 0.8)

[0.0, 0.4)

bac

baa

bab

bbc

bba

bbb

abc

aba

abb

aac

aaa

aab

000000000000000

00001

000100010

00011

001001000100

00101

001100110

00111

01010010001000

01001

010101010

01011

011011001100

01101

011101110

01111

110100100010000

10001

100110010

10011

101101010100

10101

101110110

10111

11110110011000

11001

110111010

11011

11111100

11101

11110

11111

Codeword

(a)

baa

bab

bac

babc

babb

baba

0111100 011110 01111

0111101

0111110 011111

0111111

1000000 100000 10000

1000001

1000010 100001

1000011

1000100 100010 10001

1000101

1000110 100011

1000111

1001000 100100 10010

1001001

1001010 100101

1001011

Codeword

(b)

Figure 10.1 Principle of arithmetic coding for the symbol sequence babc from event source

X ={a, b, c}, showing coding of joint probabilities: (a) up to three events with ﬁve-bit

codewords; (b) up to four events with seven-bit codewords.

10.2 Arithmetic coding 189

Given a source X =

{

, x

,...,x

}

and its probability characteristics, the coding

algorithm enables the encoding machine (encoder) to calculate rapidly the subinterval

) corresponding to any sequence a

,...,a

N −1

, where the symbols a

can

take any value, save x

. If the message source and characteristics are unknown, the

encoder must acquire the entire sequence a

, a

,...,a

N −1

, identify the different sym-

bols used (x

), and calculate the corresponding probability distribution p(x

) attached

to each of the message symbols speciﬁcally used in this sequence. We can, however,

assume that the incoming messages always use the same type of source (e.g., English

text, programming-language source code, bank dataﬁles, etc.), in which case, such an

operation simply consists of prior calibration work. In this sense, the code is adap-

tive, but it is supposed to be extensively used once it has been thus deﬁned, just like

any other variable-length static code. The key difference here with a purely static code

is that the codewords are not calculated symbol by symbol (or by symbol blocks of

predeﬁned length), but by symbol sequences having any arbitrary length. The max-

imum sequence length is deﬁned by the precision of the coding arithmetic, namely

the maximum number of bits that the machine can handle for any given codeword.

As we have seen, the use of m-bit codewords makes it possible to represent proba-

bilities with an accuracy of 1 ×2

−m

. Referring to Fig. 10.1, for instance, the ﬁve-

bit codewords deﬁne subintervals having a minimum width of 2

−5

= 1/32 = 0.03125,

exactly. This number deﬁnes the minimum difference allowed between symbol-sequence

probabilities.

As previously explained, the source’s probability distribution, including joint proba-

bilities up to some maximum order, must be calculated at ﬁrst by the encoding machine.

As soon as this initial calibration round is complete, encoding can then be performed

on the ﬂy, meaning that the codeword assignment (encoding) is performed almost at the

same rate as the message-sequence symbols a

, a

,...,a

N −1

are input to the encoder.

Such a construction consists of building up the right codeword preﬁx corresponding to

the beginning of the received sequence. Referring to Fig. 10.1, for instance, the reception

of a

= b as the ﬁrst sequence symbol does not make it possible to conclude between

00, 01, or 10 as possible two-bit preﬁxes. If the next symbol is a

= b, the machine

can make the choice of 01, since the interval of the sequence bb is described by this

preﬁx, as the ﬁgure indicates. If the next symbol is a

= a, the preﬁx is changed to

011, and so on. This shows that the encoder builds the codeword preﬁx practically at

the same rate as symbols come in, because more than one symbol may be required to

make the choice of the next preﬁx bit. If the choice is unique, this means that the

codeword is complete, and basically, that the sequence is ended. For instance, the

three-symbol sequence bbc in Fig. 10.1 yields the ﬁnal ﬁve-bit codeword 01001. In

contrast, the three-symbol sequence bbb is still at a two-bit 01 preﬁx level, and the

encoding machine is waiting for a fourth symbol to choose between the 010 or 011

preﬁxes.

As we have seen, on reaching the maximum codeword size, the termination symbol

c = x

is used by the encoder to close the message sequence, or to complete the code-

word. A nice feature is that the encoding process does not need to halt at this point.

Indeed, encoding can resume with the next incoming sequence, without any interruption.

190 Integer, arithmetic, and adaptive coding

Therefore, the encoding process may continue indeﬁnitely over time. As another feature,

the encoder may append two termination symbols cc = x

at the end of a codeword,

to instruct the decoder that the probability distribution characteristics are being main-

tained in the following message. Special terminations, or cc





... = x

n+1

n+2

...,

whose symbols are not used by the original message source, may also be appended to

the sequence for other signaling purposes, such as instructing a change in probability

distribution or in the source alphabet.

Having identical and exact knowledge of the message-source characteristics, the

decoding machine (decoder) can compute all possible subintervals [u

) to arbitrary

small widths, as permitted by the arithmetic resolution, and store them in its memory.

How this knowledge can be extracted from a program, and without communicating with

the encoder, is a complex issue. As with the encoding process, the determination of the

probability distribution is a matter of initial calibration, using the same program as the

encoder (see later). The successive message bits input to the decoder are interpreted as

codeword preﬁxes. The decoder performs the same task as reading Fig. 10.1 from right

to left. Each codeword preﬁx points to a group of subintervals stored in the decoder’s

memory. As soon as a full codeword is identiﬁed (e.g., 01001 in the ﬁgure), the memory

outputs the corresponding string (e.g., bbc). Therefore, decoding is also performed on

the ﬂy, since the memory pointer can move as fast as the message bits are received.

Like encoding, but as the reverse operation, retrieving the next symbol in the sequence

is not done on a bit-by-bit basis but out of progressive choices according to the preﬁx

patterns.

As we have seen, arithmetic coding and decoding need to compute the source’s prob-

ability distribution, with conditional probabilities of arbitrary order. A possibility is that

both encoder and decoder use the same codebook reference, but such a solution is gen-

erally not optimal, and also lacks any ﬂexibility. Rather, the system should be adaptable

to any source type, for which the characteristics may change over time, including the

size and deﬁnition of the symbol alphabet (e.g., changing from English-text language to

computer dataﬁles or digital images). The initial encoder and decoder calibration, which

provides the source’s probability distribution and conditional probabilities, requires some

initial computation steps. Let me describe here how such a computation works. From the

encoder side, the ﬁrst process consists of identifying the symbols x

and their distribution

p(x

). The idea is to monitor a sufﬁcient number of “symbol events,” in order to convert

the raw frequency histogram into an actual PDF. Because the encoder introduces the

extra termination symbol c, which is not part of the message source, the corresponding

probability p(c) must be ﬁxed to some arbitrary value, for instance, p(c) = 0.1. The ﬁrst

incoming symbol identiﬁed, say x

, is assigned the initial probability p(x

) = 0.9(which

satisﬁes p(x

) + p(c) = 1). If the second incoming symbol is different, say x

, the prob-

ability distribution becomes p(x

) = p(x

) = 0.45. This calibration process continues

until a full distribution p(x

) is obtained, with



p(x

) = 1 and c ≡ x

.Asforthe

conditional probabilities, p(a

= x

...a

k−1

), they can be assigned according to

the Laplace or the Dirichlet models. To explain the Laplace model, consider two events,

x and y.LetF

be the number of times that the event x has been counted in the sequence

...a

k−1

, and F

the count for event y. The Laplace rule deﬁnes the conditional

10.2 Arithmetic coding 191

probability as

p(a

= x|a

...a

k−1

) =

+ 1

+ F

+ 2

, (10.1)

with the same relation applying for p(a

= y|a

...a

k−1

), being obtained by inter-

changing x and y (we note that consistently, the sum of the two conditional probabilities

is equal to unity). For instance, considering the sequence xxyxxxy,wehaveF

= 5 and

= 2, thus p(a

= x|a

...a

) = 6/9 = 2/3 and p(a

= y|a

...a

) = 3/9 =

1/3. For an n-event source X ={x

, x

,...,x

}, Laplace’s rule is:

p(a

= x

...a

k−1

) =

+ 1



+ 1)

. (10.2)

Note that the Laplace rule only represents a model to determine the conditional proba-

bilities heuristically. Such an assignment is arbitrary and does not need to be exact or

accurate. What matters is that both encoder and decoder use the same deﬁnition. It can

yet be reﬁned using the Dirichlet model:

p(a

= x

,...,a

k−1

) =

+ α



+ α)

, (10.3)

where α is an adjustable constant, for instance α = 0.05 − 0.01. With the knowledge

of the distributions p(x

) and p(x

,...,a

k−1

), the encoder can then implement

the arithmetic-coding algorithm described in Appendix H. From the decoder’s side, the

calibration process is similar, except that it operates in the opposite way. The decoder,

which has the same resolution as the encoder, identiﬁes the different message codewords

received and assigns a probability interval to each possible preﬁx, as Fig. 10.1 illustrates,

reading from right to left. The correspondence between the identiﬁed codewords and

the original source symbols is only a matter of convention, like the A–Z sequence of

characters in the English alphabet.

It can be shown that arithmetic coding is near optimal, as the codeword length, l(s),

for a given symbol sequence, s, closely approaches the Shannon limit −log p(s), which

represents the information contents of the sequence. Owing to its versatility with respect

to source types and its capability of coding and decoding “on the ﬂy,” arithmetic coding

is used in many still or motion image-compression standards, such as JPEG and MPEG

(see Appendix G).

Another interesting application of arithmetic coding concerns the generation of ran-

dom numbers. Indeed, random-bit strings can be generated by feeding an arithmetic

decoder with uniformly distributed bit streams, such as produced by a pseudo-random

word generator.

The decoder then outputs what it interprets to be a suite of sym-

bol sequences picked up within the [0, 1) probability interval. The symbol sequences

form random bit streams having probability-distribution characteristics departing from

uniformity, i.e., p(x

= 0) = p(x

= 1).

A pseudo-random word can be a pre-established bit pattern with uniform 1/0 bit distribution, which is

cyclically repeated by bit translation or permutation.

192 Integer, arithmetic, and adaptive coding

Arithmetic coding can also be used for fast data-entry devices. The principle is for

a human operator to acquire information and produce a maximum of information bits

through a minimal number of body gestures. A computer keyboard only provides the one-

to-one correspondence between alphanumerical characters and their ASCII codewords.

The keyboard is designed to have the most frequently used letters in speciﬁc locations

that the ten ﬁngers learn to reach automatically, without searching. Let us imagine

instead a fancy dynamic keyboard, where the most frequently used letters and most

likely letter groups would always be found near the last character that was entered, like

ﬁnding he immediately after typing t or nd after a, corresponding to the words the and

and, respectively. Ready-made word terminations, like cept, dition, stitute, tinue, vey,

and vention, would show up as soon as the text con had been input to the keyboard, for

instance. These word terminations could also be arranged according to their frequent

use in the speciﬁc message context. Such a dynamic keyboard would make it possible

to achieve rapid text acquisition using a single-click, perhaps with a mouse or an optical

or eye pointer or tracker. A representative application of this principle is provided by the

project Dasher (European languages), also named Daishoya (Japanese).

It consists of

a text-entry interface, which can be driven by natural pointing gestures, using a joystick,

a touch-screen, a tracker or roller ball, a mouse, or even an eye tracker. Experienced

readers can perform text acquisition with a single ﬁnger or eye motion at rates of 20 to 40

words per minute, which is nearly as fast as the normal writing rate and even faster in the

last case. Practical device applications concern palmtop computers, wearable computers,

one-handed computers, and hands-free computers for various working environments and

for the disabled.

10.3 Adaptive Huffman coding

Adaptive Huffman coding is also known as FGK,afterFaller, Gallager and Knuth, and

as algorithm V, after improvements of FGK from Vitter.

The FGK principle represents a dynamic implementation of Huffman coding trees,

which is based on a running estimate of the symbol probability distribution. The code

is optimal but only within the context of a given source message. Both encoder and

decoder adapt themselves to the changing probability distribution, which makes the

method suitable to encode or decode time-evolving or nonstationary sources.

The key advantage of adaptive vs. static Huffman coding is that the data encoding

and decoding is, indeed, performed “on the ﬂy,” through a single-pass conversion pro-

cess. In contrast, the static scheme requires two passes: the ﬁrst one for the coding-tree

determination, the second for the coding. However, if the source’s characteristics are

time-invariant, this operation only needs to be performed once, and the other incom-

ing message sequences are coded and decoded through a single pass. If the source’s

See details with animated screenshot demonstrations in www.inference.phy.cam.ac.uk/dasher; the software

is freely available.

See: D. A. Lelewer and D. S. Hirschberg, Data compression. Computing Surveys, 19 (1987), 261–97,

www.ics.uci.edu/∼dan/pubs/DataCompression.html.

10.3 Adaptive Huffman coding 193

Root

0.6

0.3

0.10

0.3

0.4

0.04

0.06

0.20

0.17

0.13

Root

0.6

0.37

0.2

0.23

0.4

0.06

0.04

0.17

0.13

0.10

(a)

(b)

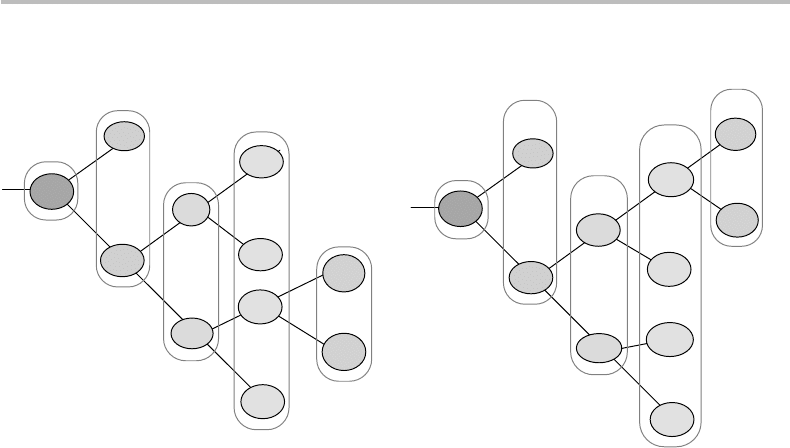
Figure 10.2 Example of source coding tree (a) without sibling property, and (b) with sibling

property (Huffman tree). The number shown inside each node’s circle is the corresponding

probability, and in case (b) the nodes are labeled 0 to 11.

characteristics evolve rapidly, however, then the coding tree must be re-evaluated for

each message sequence, which justiﬁes the interest of the single-pass adaptive method.

The FGK algorithm uses what is called the sibling property of coding trees, as

introduced by Gallager.

This algorithm is deﬁned as follows:

A coding tree has a sibling property in the case where all nodes, except the root and the terminal

(leaf) nodes, have a sibling node and can be listed in order of nondecreasing weights.

To grasp the meaning of this seemingly obscure deﬁnition, and understand

the concept of “sibling property,” consider the two illustrative examples shown

in Fig. 10.2. The two coding trees shown in Fig. 10.2 are associated with the

same source X ={A, B, C, D, E, F }, whose probability distribution is p(x

) =

{0.4, 0.2, 0.17, 0.13, 0.06, 0.04}. The weights (or combined probabilities) of each of

the nodes are indicated. Except for the root node at left, and the leaf nodes at right,

intermediate nodes are seen to come with a sibling of equal or lower weight. Looking

at the tree (a) in the ﬁgure, we observe that there are ﬁve sibling pairs responding to

this description. However, the group formed by the pairs (0.2–0.1) and (0.17–0.13) is

not ordered according to increasing or decreasing weights. The above-stated “sibling

property” rule requires that the nodes be arranged by successive pairs of nondecreasing

weights, (0.1–0.13) then (0.17–0.2), and this is precisely the case of the second tree

(b) shown in Fig. 10.2. Not surprisingly, this rule “compliant” tree is a Huffman tree,

as one may easily check. Also, Gallager showed another powerful property, according

to which

A binary preﬁx code is a Huffman code if and only if its coding tree has the sibling property.

See: R. G. Gallager, Variations on a theme by Huffman. IEEE Trans. Inform. Theory, 24 (1978), 668–74.

194 Integer, arithmetic, and adaptive coding

The implementation of the FGK algorithm proceeds as follows. At the start, the tree

is a single leaf node, which is referred to as the Ø-node. Assume that there are n symbols

in the message sequence to be encoded. The encoder does not need to know what n

might be. The idea is always to keep the ∅-node for the n − m symbols that have not

been observed yet by the encoder, and to compute the Huffman coding tree for the other

m symbols, out of an observed sequence of k symbols. The resulting coding tree is a

Huffman tree h(k), which has k + 1 leaves: one leaf is the ∅-node (probability or weight

zero) and the other k leaves represent the k symbols (nonzero probabilities or weights),

ordered by siblings of nondecreasing weights, and labeled in that order. Whenever a

new or previously unobserved symbol is identiﬁed, the ∅-node is split into a new ∅-node

and a new leaf node is created for this symbol. The coding tree is also reconﬁgured.

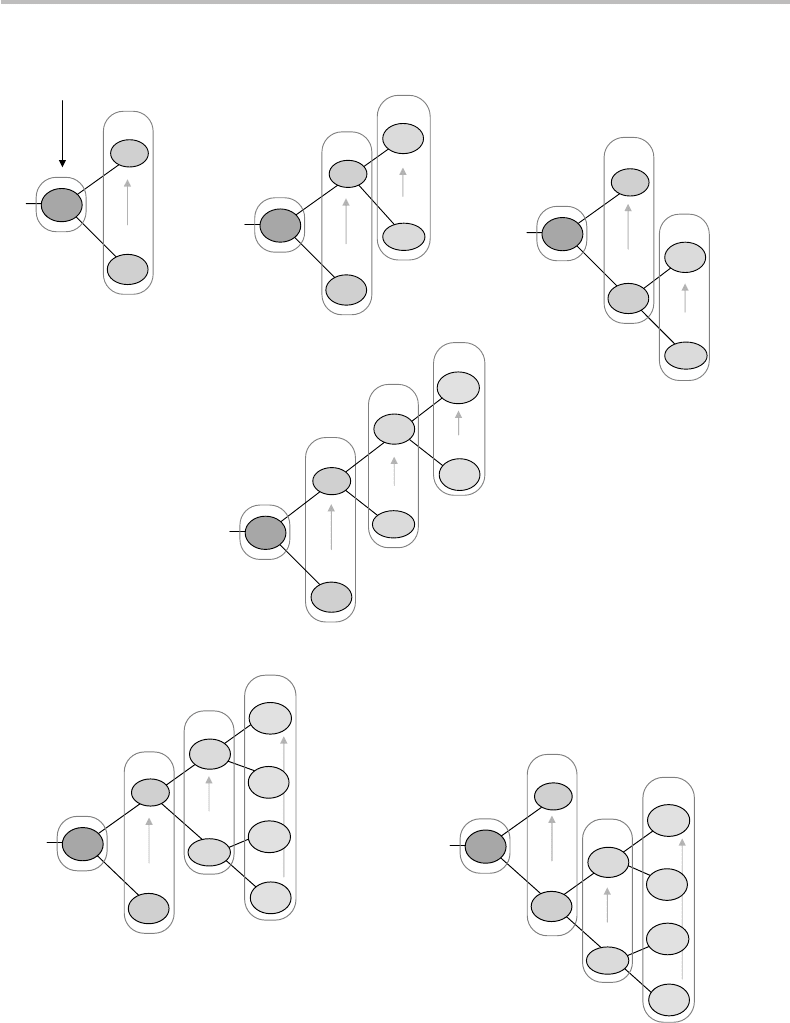
Figure 10.3 illustrates the evolution of the coding tree, as recomputed at each step for

the 12-symbol sequence example GOODTOSEEYOU, from step k = 1(G) to step k = 6

(GOODTO).

From the orderly sequence of node weights, we observe that all trees in Fig. 10.3

have the sibling property. The evolving codeword assignment for each different symbol

(G, O, D, T, S, E, Y, U, ∅), as determined by both encoder and decoder from the same

static Huffman algorithm, is also shown in the ﬁgure. The symbol codewords up to step

k = 12 are shown in Table 10.3. We observe from the table that, as expected, the codeword

assignment changes at each computational step k. The table also shows, for each step

k, the value of entropy H, the mean codeword length L, and the corresponding coding

efﬁciency η. The entropy and coding efﬁciency are plotted in Fig. 10.4. We observe from

the ﬁgure that the entropy increases with the message length, following a sawtooth pat-

tern. The entropy’s slope progressively decreases while remaining globally positive. The

occasional downward slope changes correspond to the accidental occurrence of repeated

symbols, which decreases the mean uncertainty or Shannon information. Clearly, the

drops observed at k = 6 and k = 11 can be attributed to the repeated occurrences of O

in the GOODTOSEEYOU message sequence. For a sufﬁciently long message sequence,

it is expected that the entropy reaches the limit of that of the English-language source,

whichwasshowninChapter 4 (1982 poll) to be H = 4.185 bit/symbol. Such a con-

vergence must be quite rapid, since a message as short as GOODTOSEEYOU has the

entropy of H = 2.751 bit/symbol (Table 10.3), which represents 66% of this limit.

We also observe from Fig. 10.4 that the coding efﬁciency rapidly converges to 100%

as new symbols come in, although with a similar saw-tooth progression for entropy.

With this message-sequence example, the efﬁciency reached at k = 12 is η = 91.72%

(Table 10.3), a relatively high performance due to the optimality of the Huffman coding

(the mean codeword length L always remaining within one bit of the source entropy H ,

as the table data also indicate).

As we have seen, the encoder dynamically updates its coding tree at each step k,

starting with a single ∅-node leaf. From the receiving side, the decoder just has to

perform the same operation. However, for the decoder to update its coding tree, it needs

the following basic information:

(a) For a new symbol: the ∅-node’s current codeword and the new symbol deﬁnition;

(b) For a symbol previously observed: the symbol’s current codeword.

10.3 Adaptive Huffman coding 195

Root

= 1

∅

(

)

= 2

∅

(GO)

= 3

∅

(GOO)

= 4

∅

001

(GOOD)

000

(a)

= 5

(GOODT)

(GOODTO)

∅

011

000

010

001

= 6

100

∅

111

110

101

(b)

Figure 10.3 Evolution of the adaptive Huffman coding tree with the message example

GOODTOSEEYOU. The index k is the number of symbols received: (a) k = 1–4; (b) k = 5–6.

Nodes are relabeled according to the sibling-property rule. The number inside each node’s circle

is the corresponding weight. The steady or changing codewords associated with each symbol are

shown at the right. The evolution of the coding tree and codeword assignment up to k = 12 is

shown in Table 10.3.

Table 10.3 Evolution of coding tree according to the

adaptive Huffman coding algorithm

with the 12-symbol message example GOODTOSEEYOU. The index k

is the number of symbols received. A possible codeword assignment to each symbol, including that of the ∅-node, is shown for each step. See Fig. 10.3 for the

corresponding coding trees up to step k = 6. The entropy and coding efﬁciency are plotted in Fig. 10.4.

Symbol k = 1 k = 2 k = 3 k = 4 k = 5 k = 6 k = 7 k = 8 k = 9 k = 10 k = 11 k = 12

G 0 1 10 01 1 111 001 010 011 100 100 101

O 00 0 1 000 0 1 00 00 01 00 01

D 000 001 110 010 011 100 101 101 10

T 010 101 011 100 101 110 110 111

0000 101 010 111 111 0000

110 11 000 010 001

0010 0110 0001

1000

∅ 1 01 11 001 011 100 0001 111 0101 0011 0011 1001

Source entropy H (bit/symbol) 0 0.5 0.918 1.5 1.921 1.792 2.128 2.405 2.419 2.646 2.550 2.751

mean codeword length L (bit/word) 1 1.5 1.333 1.75 2.200 2.000 2.285 2.625 2.777 2.800 2.727 3.000

Coding efﬁciency η (%) 0.00 33.33 68.87 85.71 87.36 89.62 93.10 91.64 87.10 94.52 93.51 91.72