Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

10.5 Exercises 207

The LZ algorithm family has led to several data-compression standards and ﬁle-archival

utilities known as Zip (from LZC), GNU zip or gzip (from LZ77), PKZIP (from LZW),

PKARK, Bzip/Bzip2, ppmz, pack, lzexe (a MS-DOS utility), and compress (from LZC

and LZW, a UNIX utility), for instance. Such programs make it possible to compress

most ASCII-source ﬁles by a factor of two, and sometimes up to three, but with differ-

ent performance and computing speeds.

The algorithm LZW is also used for image

compression in the well-known formats called GIF (graphic interchange format) and

TIFF (tagged image ﬁle format); for instance, GIF has become a leading standard for

the exchange of graphics on the World Wide Web. The original LZ77 algorithm is used

in the patent-free image format PNG (portable network graphics). See Appendix G for

a more detailed description of data and image compression standards.

10.5 Exercises

10.1 (B): Determine the coding efﬁciency corresponding to the symbol source deﬁned

in Table 10.7, using Elias-gamma and Elias-delta codes.

Table 10.7 Data for Exercise 10.1.

Symbol xp(x)

A 0.302

B 0.105

C 0.125

D 0.025

E 0.177

F 0.016

G 0.125

H 0.125

10.2 (T): Determine the Fibonacci code of order m = 3 up to the ﬁrst 31 integers

(Clue: use level-three coding and be sure to obtain a preﬁx code).

10.3 (M): Determine the Golomb code with parameter m = 3 for integers i = 0to

i = 12.

10.4 (M): Determine the step-by-step coding assignment in dynamic Huffman coding

for the message sequence AABCABB and the resulting coding efﬁciency.

10.5 (M): Determine a Lempel–Ziv code for the 30-symbol sequence

ABBABBBABABAAABABBBAABAABAABAB

and the corresponding compression rate.

See: D. A. Lelewer and D. S. Hirschberg, Data compression. Computing Surveys, 19 (1987), 261–97,

www.ics.uci.edu/∼dan/pubs/DataCompression.html and D. J. C. MacKay, Information Theory, Inference

and Learning Algorithms (Cambridge: Cambridge University Press, 2003).

11 Error correction

This chapter is concerned with a remarkable type of code, whose purpose is to ensure that

any errors occurring during the transmission of data can be identiﬁed and automatically

corrected. These codes are referred to as error-correcting codes (ECC). The ﬁeld of

error-correcting codes is rather involved and diverse; therefore, this chapter will only

constitute a ﬁrst exposure and a basic introduction of the key principles and algorithms.

The two main families of ECC, linear block codes and cyclic codes, will be considered.

I will then describe in further detail some speciﬁcs concerning the most popular ECC

types used in both telecommunications and information technology. The last section

concerns the evaluation of corrected bit-error-rates (BER), or BER improvement, after

information reception and ECC decoding.

11.1 Communication channel

The communication of information through a message sequence is made over what

we shall now call a communication channel or, in Shannon’s terminology, a channel.

This channel ﬁrst comprises a source, which generates the message symbols from

some alphabet. Next to the source comes an encoder, which transforms the symbols or

symbol arrangements into codewords, using one of the many possible coding algorithms

reviewed in Chapters 9 and 10, whose purpose is to compress the information into the

smallest number of bits. Next is a transmitter, which converts the codewords into physical

waveforms or signals. These signals are then propagated through a physical transmission

pipe, which can be made of vacuum, air, copper wire, coaxial wire, or optical ﬁber.

At the end of the pipe is a receiver, whose function is to convert the received signals into

the original codeword data. Next comes a decoder, which decodes and decompresses

the data and restitutes the original symbol sequence to the message’s recipient. In an

ideal communications channel, there is no loss, nor is there any alteration of the message

information thus communicated. But in realistic or nonideal channels, there is always

a ﬁnite possibility that a part of this information may be lost or altered, for a variety of

physical reasons, e.g., signal distortion and additive noise, which will not be analyzed

here. The only feature to be considered here is that a fraction of the received codewords

or symbols may differ from the ones that were transmitted. In this case, it is said that

there exist symbol errors.

11.1 Communication channel 209

Figure 11.1 Basic layout of error-correction (EC) coding and decoding within a communication

channel (OH = overhead).

We may just see ECC as another type of coding step or “coding layer,” which is to be

inserted in the message transmission chain. More speciﬁcally, error-correction encoding

should be performed after data encoding (prior to transmission) and decoding (error

correction) should be performed before data decoding (after reception), as illustrated in

Fig. 11.1. As the ﬁgure indicates, the coded message to be transmitted is now referred

to as a payload. Let us refer to the originator’s message as the data payload.Thekey

purpose of ECC is to ensure that the payload arrives at the destination with the smallest

possible probability of symbol errors. The tax to pay for ECC implementation is that

some additional information must be included in the message code, referred to as control

bits. Such control bits, which disappear after ECC decoding, correspond to what is called

overhead information, or “overhead” for short.

How does ECC work? A ﬁrst and most basic approach consists of appending a certain

number of redundancy bits to the payload data. The decoder then uses these redundancy

bits to decide whether (a) the payload bits have been properly detected, and (b) any

resulting corrective action is required to restore the “errored” bit (as telecom jargon

goes) to their correct initial value. An obvious redundancy scheme is to repeat the

210 Error correction

information a certain number of times. It is just like communicating a phone number or

someone’s name over a poor telephone connection or in noisy surroundings. By repeating

the information two or three times, the hope is that the number or the name spelling is

going to be unambiguously communicated. For instance, one can transmit 0000 instead

of a single 0 symbol, and 1111 instead of a single 1 symbol. According to this code, the

received sequence (underscores introduced for clarity)

0010

1111 0111 1011

is interpreted as very likely to represent the payload message:

0000

1111 1111 1111.

In the above guess of the correct message, we have followed an intuitive rule of majority

logic. The bit errors were automatically corrected based on the fact that the three bit

anomalies in the four-bit groups were easily identiﬁable. However, there is no absolute

certainty that such an intuitive “majority-rule” decoding may yield the actual payload.

Indeed, if two errors occur in any of the above four-bit words (however less likely the

event), receiving 1100 or any other permutation thereof could be decoded as 1111 or

0000, while the correct codeword could have been either 0000 or 1111, which represents

an undecidable problem. In such a case, majority logic fails to correct errors, unless more

redundancy bits are used. Clearly, decoding reliability grows with increasing information

redundancy and overhead, but at the expense of wasting the channel transmission capacity

(a concept that we will have to develop in the next chapter).

The two following sections describe efﬁcient and far smarter ways to correct bit errors

with minimal redundancy or overhead, as based on the two main ECC families called

linear block codes and cyclic codes.

11.2 Linear block codes

A ﬁrst possible strategy for error correction is to transmit the information by slicing

it into successive blocks of a ﬁxed, n-bit length. By convention, the ﬁrst segment of

the block is made of k payload bits, corresponding to 2

possible (payload) message

sequences. The second segment is made of m = n − k bits, which we shall call parity

bits, and which will be used for EC coding. These m parity bits represent the overhead

information. We thus have an (n, k) block made of n bits, which contains k payload bits,

and n − k parity bits. This arrangement is most generally referred to as a linear block

code.

By deﬁnition, the bit rate B is the number of payload bits generated or received per

unit time (e.g., B = 1 Mbit/s). It is also the rate at which payload bits are encoded by the

transmitter and decoded by the receiver, in the absence of ECC. The code rate is deﬁned

as the ratio R = k/n, which represents the proportion of payload bits in the block (1 − R

representing the redundancy or overhead proportion). To provide decoded or corrected

data at the initial payload-bit-rate B, the encoded-block bit rate should be increased by

a factor 1/R, corresponding to a percent additional bandwidth of 1/R − 1, which is

11.2 Linear block codes 211

referred to as the percent bandwidth expansion factor. The rate at which bit errors are

detected is called the bit error rate (BER). The key effect of ECC is, thus, to reduce the

BER by orders of magnitude, literally! The intriguing fact, however, is that there is no

such a thing as “absolute” error correction, which would provide BER = 0 × 10

to all

orders. The reality is that ECC may provide BER reduction to any arbitrary order, but

there is a tax to pay for reaching this “absolute” by means of increasingly sophisticated

ECC algorithms with increasingly longer overheads.

How do ECC linear block codes work? The task is to ﬁnd out an appropriate coding

algorithm for the parity bits, making it possible, on EC decoding, to detect and correct

errors in the received block, with adequate or target precision. Because such an algorithm

begins with the input data, the approach is called forward error correction, or FEC.

The following description requires some familiarity with basic matrix-vector formalism.

We focus now on how linear block codes are actually generated. Deﬁne ﬁrst the input

message/payload bits by the k-vector X = (x

...x

), and the block code (EC encoder

output) by the n-vector Y = (y

...y

). The block-code bits y

are calculated from the

linear combination:

= g

+ g

+···+g

, (11.1)

where g

(l = 1...k, m = 1...n) are binary coefﬁcients. This deﬁnition can be put

into a vector-matrix product, Y = X

G, or, explicitly,

Y = (y

...y

) = (x

... x

)







... g

... ... g







≡ X

G. (11.2)

The matrix

G is called the generator matrix. It is always possible to rewrite the generator

matrix under the so-called systematic form:

G = [I

|P] =







1 ... ... 0

0 ... ... 1

... p

... ... p







, (11.3)

where I

is the k × k identity matrix (which leaves the k message bits unchanged) and

P is an m × k matrix which determines the redundant parity bits. Thus the encoder

output Y = X

G = X[I

|P] is a payload block of k bits followed by a parity block of

m = n − k bits.

This arrangement, where the payload bit-sequence is left unchanged

by the EC encoder, is called a systematic code.

There exist possibilities for backward error correction (BEC), but the approach means some form of

backward-and-forward communication between the two ends of the channel, at the high expense of channel

use or bandwidth waste.

Note that in another possible convention for the systematic form/code, as described in some textbooks, the

parity bits may instead precede the payload bits.

212 Error correction

For future use, we deﬁne the n × m parity-check matrix:

H = [P

] =







... p

... ... p

1 ... ... 0

0 ... ... 1







, (11.4)

where P

is the transposed matrix of P (note how their coefﬁcients are symmetrically

permuted about the diagonal elements). We note then the important property

= GH

= 0, (11.5)

which stems from

= [P

] ·





= P

+ P

≡ 0 = (HG

)

= GH

. (11.6)

In this expression, we have used the property that for binary numbers x,thesumx + x

is identical to zero (0 + 0 = 1 + 1 ≡ 0). From the property in Eq. (11.5), we have

= 0, (11.7)

which stems from Y

≡ X

= X (

) = 0.

We consider now the received block code, which we can deﬁne as the n-vector Z.

Since the received block code is a “contaminated” version of the original block code Y ,

we can write Z in the form:

Z = Y + E, (11.8)

where E is an error vector whose ith coordinate is 0 if there is no error and 1 otherwise.

Post-multiplying Eq. (11.8)by

and using the property in Eq. (11.7), we obtain

S = Z

= (Y + E)

= E

. (11.9)

The m-vector S is called the syndrome. The term “syndrome” is used to designate the

information helping to diagnose a “disease,” which, here, is the error “contamination”

of the signal. A zero-syndrome vector means that the block contains no errors (E =

0).

As the example described next illustrates, single-error occurrences (E has only one

nonzero coordinate) are in one-to-one correspondence with a given syndrome S. Thus

when computing the syndrome S = Z

at the receiver end, one immediately knows

two things:

(a) Whether there are errors, as indicated by S =

(b) In the assumption that it is a single-error occurrence, where it is located.

At this point, we should illustrate the process of error detection and error correction

through the following basic example.

Consider the block code (n, k) = (7, 4), which has k = 4 message bits and m = 3

parity bits. Such a block, which is of the form n = 2

− 1 and k = n − m, with m ≥ 3,

11.2 Linear block codes 213

Table 11.1 Message words and corresponding block

codes in an example of a Hamming code (7.4).

Message word X Block code Y

0000 0000 000

0001 0001 111

0010 0010 011

0011 0011 100

0100 0100 101

0101 0101 010

0110 0110 110

0111 0111 001

1000 1000 110

1001 1001 001

1010 1010 101

1011 1011 010

1100 1100 011

1101 1101 100

1110 1110 000

1111 1111 111

is referred to as a Hamming code. According to the deﬁnition in Eq. (11.3), we deﬁne

the following generator matrix (out of many other possibilities)

G =







1000

0100

0010

0001

110

101

011

111







, (11.10)

which gives, from Eq. (11.4), the parity-check matrix

H =





1101

1011

0111

100

010

001





(11.11)

and its transposed version







110

101

011

111

100

010

001







. (11.12)

The 2

= 16 possible message words X and their corresponding block codes Y ,as

calculated from Eqs. (11.2) and (11.10), are listed in Table 11.1. For clarity, the parity

bits are shown in bold numbers. As expected, the block codes are made of a ﬁrst sequence

214 Error correction

(1,0)

(1,1)

(0,1)

(0,0)

(1,1,0)

(1,0,0)

(0,0,0)

(0,1,0)

(1,1,1)

(0,1,1)

(1,0,1)

(0,0,1)

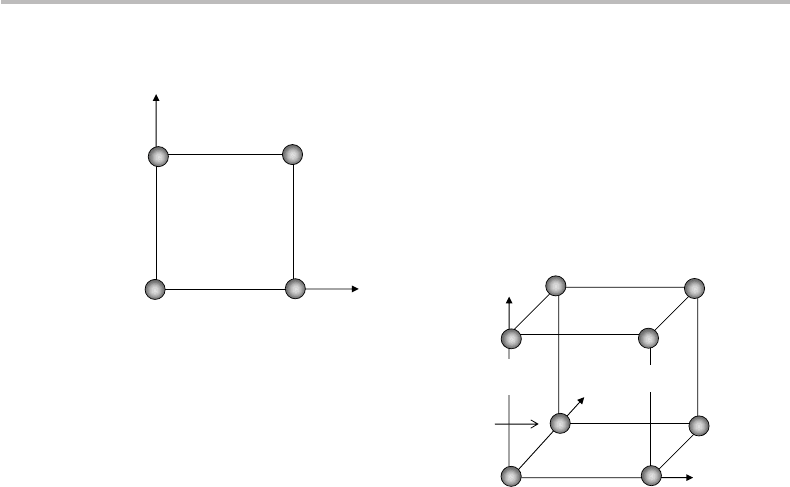
Figure 11.2 Placing codewords of two or three bits in the vertices of a square or a cube,

respectively, to illustrate Hamming distance.

of four (original) messages bits followed by a second sequence of three parity bits. For

instance, the message codeword 0111 is encoded into the block code 0111 001, where

the three bits on the right are the parity bits.

For future use, I introduce the following deﬁnitions in ECC formalism:

Hamming weight w(X): number of 1 bits in a given (block) codeword X .

Hamming distance d(X, Y ) between two codewords X, Y : number of bit positions

in which the two codewords differ; consequently, the Hamming weight w(X )isthe

distance between a given codeword X and the all-zero codeword; also note the property

d(X, Y ) = w(X + Y ) = w(X − Y ).

Minimum Hamming distance d

min

: minimum number of 1 bits in the block codewords

(excluding the all-zero codeword). Consequently, d

min

is also the minimum number

of bit positions by which any codeword differ. It is readily checked from the example

in Table 11.1 that d

min

= 3, which is a speciﬁc property of Hamming codes.

It should be noted that the Hamming distance is a mathematical distance in the strict

deﬁnition of the term, as described in Chapter 5, when introducing the Kullbach–

Leibler distance between two probability distributions. To illustrate the meaning of

Hamming distance, Fig. 11.2 shows that it is possible to place all the different two-

bit or three-bit codewords ((a

)or(a

)) on the vertices of a square or a cube,

following the Cartesian coordinate system x = a

, y = a

, z = a

, which corresponds

to the vectors (x, y, z) = (a

, a

). According to deﬁnition, the Hamming distance

between codeword (0, 0) and (1, 0) or (1, 1) is d = 1ord = 2, respectively. Likewise,

the distance between (0, 0, 0) and (1, 0, 0) or (1, 0, 1) or (1, 1, 1) is d = 1ord = 2or

11.2 Linear block codes 215

Table 11.2 Syndrome vector S = (s

, s

)

associated with single-error patterns E =

, e

) in the Hamming block

code (7, 4) deﬁned in Table 11.1.

Error pattern E Syndrome S

0000000 000

1000000 110

0100000 101

0010000 011

0001000 111

0000100 100

0000010 010

0000001 001

d = 3, respectively. We see from the illustration that the Hamming distance does not

correspond to the Euclidian distance, but rather to the smallest number of square or cube

edges to traverse in order to move from one point to the other.

Going back to our (n, k) = (7, 4) block code example, assume next that the received

block Z contains a single bit error, whose position in the block is unknown. If the error

concerns the ﬁrst bit of Z = Y + E, this means that the value of the ﬁrst bit of Y has been

increased (or decreased) by 1, corresponding to the error vector E = (1, 0, 0, 0, 0, 0, 0).

For an error occurring in the second bit, we have E = (0, 1, 0, 0, 0, 0, 0), and so on,

to bit seven. For each single-error occurrence, we can then calculate the corresponding

syndrome vector using the relation S = E

in Eq. (11.9). The result of the computation

is shown in Table 11.2. It is seen that a unique syndrome corresponds to each error

occurrence. For instance, if the syndrome is S = (0, 1, 1), we know that a bit error

occurred in the third position of the block sequence, and correction is made by adding 1

to the bit (equivalently, by switching its polarity, or by adding E to Z ). Thus any single-

error occurrence (whether in payload or in parity bit ﬁelds) can be readily identiﬁed and

corrected.

What happens if there is more than one error in the received block? Consider the

case of double errors in our (n, k) = (7, 4) example. The possibilities of a single bit

error correspond to seven different error patterns. For double errors, the number of

possibilities is C

= 7!/[2!(7 − 2)!] = 21, corresponding to 21 different error patterns.

Since the syndrome is only three bits, it can only take 2

− 1 = 7 conﬁgurations. Thus,

the syndrome is no longer associated with a unique error pattern. Here, the seven

syndrome conﬁgurations correspond to 7 + 21 = 28 error patterns of either one- or two-

bit errors. It is an easy exercise to determine the actual number of error patterns associated

with each syndrome. For instance, the results show that S = (0, 0, 0), S = (0, 0, 1), S =

(0, 1, 1) and S = (1, 0, 1) are associated with one, two, three and four patterns of two-bit

errors, respectively. Thus, syndrome decoding can only detect the presence of errors, but

cannot locate them with 100% accuracy, since they are associated with more than one

error pattern. It is clear that with Hamming codes having greater numbers of parity bits,

this imperfect correction improves in effectiveness, as the mapping E → S becomes

216 Error correction

less redundant. The approach is, however, costly in bandwidth use, and error correction

is, as we have announced, not “absolutely” efﬁcient. This situation illustrates the fact that

in most cases, syndrome decoding cannot determine the exact error pattern E, but only

the one that is most likely to correspond to the syndrome, E

. The Hamming distance

between E and E

is minimized but is nonzero. Therefore, the substitution Z → Z + E

represents a best-choice correction rather than an exact corrective operation. This is

referred to as maximum-likelihood decoding.

As we have seen, the 2

n−k

different syndromes allow the absolute identiﬁcation of

any single bit error in the (n, k) block code. Yet, each of these vectors corresponds to a

ﬁnite number of multiple bit errors, albeit such occurrences are associated with lower

and rapidly decreasing probabilities. For a block code of length n, there actually exist 2

possible error patterns (from zero to n bit errors). Out of these sets of error possibilities,

syndrome decoding is able to detect and correct 2

single bit errors, as we have seen

earlier. What about the remaining error patterns, which contain more than one bit error?

These are of two kinds. Since the block code has 2

block codewords, there exist:

(a) 2

error patterns that exactly match any of the block codewords or belong to the

block codeword set, and (b) 2

− 2

error patterns that do not belong to the block

codeword set. In case (a), the syndrome vector is identical to zero (S = (0, 0, 0)), which

means that the errors remain undetected (and for that matter, uncorrected). In case (b),

the syndrome vector is nonzero (S = (0, 0, 0)), which indicates the existence of errors,

but, as we have seen, such multiple bit errors cannot be corrected. Consider the ﬁrst

case (a) where the code fails to detect any error, and let us estimate the corresponding

probability, q(E). It is easily established that this probability is given by

q(E) =



i=1

(1 − p)

n−i

, (11.13)

where p is the probability of a single bit error and A

is the number of block codewords

having a Hamming weight of i (to recall, having i bits equal to one). We note that A

for

i = 1,...,d

min

− 1. It is left as an exercise that in our (n, k) = (7, 4) code example, we

have q(E) < 10

−8

for p ≤ 10

−3

, and q(E) < 10

−14

for p ≤ 10

−5

, which illustrates that

the likelihood of the code to fail in detecting any errors is comparatively small, even at

single-bit-error rates as high as p = 10

−5

− 10

−3

In view of the above, the key question coming to mind is: “Given a block code, what

is the maximum number of errors that can be detected and corrected with absolute

certainty?” The rigorous answer to this question is provided by a fundamental property

of linear block codes. This property states that the code has the power to correct any

error patterns of Hamming weight w (or any number of w errors in the block code),

provided that

w ≤



min

− 1

, (11.14)

where d

min

is the minimum Hamming distance, and where the brackets {x} indicate the

largest integer contained in the argument x, namely {(d

min

− 1)/2}=(d

min

− 1)/2.

A formal demonstration of this property is provided in Appendix J. What about error