Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

8.4 Mean code length and coding efﬁciency 137

= 2.640 trit/symbol. We, thus, ﬁnd that η = 74.5%. As we shall see further in this

chapter, such a ratio deﬁnes coding efﬁciency, a parameter that cannot exceed unity. Put

simply:

The mean codeword length (or effective code entropy) cannot exceed the source entropy.

This is a fundamental property of codes, which was originally demonstrated by Shannon.

We can thus conclude that with a 74% coding efﬁciency, the Morse code (analyzed as

a ternary code) is a reasonably good choice. Yet, despite its popularity and usefulness

in the past (and until as recently as 1999), the Morse code is quite far from optimal.

The main reason for this is the use of the blank, which is ﬁrst required for the code to

be uniquely decodable, and second for being usable by human operators. Such a blank,

however, does not carry any information whatsoever, and it takes precious codeword

resources! This observation shows that we could obtain signiﬁcantly greater coding

efﬁciencies if the Morse code was uniquely decodable without making use of blanks.

This improved code could be transmitted as uninterrupted bit or trit sequences. But it

would be only intelligible to machines, because human beings would be too slow to

recognize the unique symbol patterns in such sequences. Considering then both binary

and ternary codings (with source entropies H

source

showninTable8.3), and either ﬁxed

or variable symbol or codeword sizes, there are four basic possibilities:

(i) Fixed-length binary codewords with l = 5 bit (2

= 32), giving L ≡ 5.000 bit/

symbol, or H

source

/L = 83.7%;

(ii) Fixed-length ternary codewords with l = 3 trit (3

= 27), giving L ≡ 3.000 trit/

symbol, or H

source

/L = 88.0%;

(iii) Variable-length binary codewords with lengths between l = 1 and l = 10 bits, gi-

ving L ≡ 4.212 bit/symbol, or H

source

/L = 99.33% (with optimal codes using

3 ≤ l ≤ 9 bits);

(iv) Variable-length ternary codewords with lengths between l = 1 and l = 3 trits,

giving L ≡ 2.744 trit/symbol or H

source

/L = 96.2%.

The result shown in case (iii) is derived from an optimal coding approach (Huffmann

coding) to be described in Chapter 9. The result shown in case (iv) will be demonstrated

in the next section. At this stage, we can just observe that all the alternative solutions

(i)–(iv) have coding efﬁciencies signiﬁcantly greater than the Morse code. We also note

that the efﬁciency seems to be greater for the multi-level (M-ary) codes with M > 2,

but I will show next that it is not always true.

Consider, for simplicity, the case of ﬁxed-length M-ary codes, for which it is straight-

forward to calculate the coding efﬁciency. For instance, quaternary codewords, made

with n quad characters, called 0, 1, 2, and 3, can generate 4

symbol possibilities.

Since 4

< 26 < 4

= 64, codewords with 3 quads are required for the A–Z alpha-

bet. The mean codeword length is, thus, L = 3 quad/symbol. The source entropy is

= (ln 2/ln 4) H

= 2.092 quad/symbol. Thus, the coding efﬁciency is η = H

/L =

69.7%, which is lower than that of ternary, ﬁxed-length coding (88.0%), as seen in case

(ii). The reason is that going from ternary to quaternary coding does not reduce the

codeword length, which remains equal to three. The situation would be quite different

138 Information coding

if we used variable-length codewords, since a single quad can represent four possibil-

ities, instead of three for the trit. Let us look at the extreme case of a 26-ary coding,

i.e., a coding made of 26 alphabet characters (called 26-its) which can be represented,

for instance, by an electrical current with 26 intensity levels. Each codeword is, thus,

made of a single 26-it, and the mean codeword length is L = 1 26-it/symbol. The source

entropy is H

= (ln 2/ ln 26)H

= 0.890 26-it/symbol. The coding efﬁciency is, there-

fore, η = H

/L = 89.0%, which represents the highest efﬁciency for a ﬁxed-length

coding (one character/symbol) of the A–Z source. However, if we relate this last result

to the efﬁciency of a variable-length binary or ternary code, cases (iii) and (iv) above,

we see that the second yields higher performance.

The main conclusions of the above analysis are:

(1) The Morse code can be viewed as being a variable-length ternary code; it is quite

efﬁcient for human-operator use, but not for binary or ternary machines;

(2) One can code symbols through either ﬁxed-length or variable-length codewords,

using any M-ary representation (M = number of different code characters or code

alphabet size);

(3) The mean codeword length (L) represents the average length of all possible source

codewords; it cannot be smaller than the source entropy (H), which deﬁnes a coding

efﬁciency (L/H ) with a maximum of 100%;

(4) For ﬁxed-length codewords, one can increase the coding efﬁciency by moving from

binary to M-ary codes (e.g., ternary, quaternary, . . . ), the efﬁciency increasing with

M, continuously or by steps;

(5) The coding efﬁciency can be increased by moving from ﬁxed-length to variable-

length codewords (the shortest codewords being used for the most likely source

symbols and the reverse for the longest codewords).

The property (3), known as Shannon’s source coding theorem, and the last property (5)

will be demonstrated next.

8.5 Optimizing coding efﬁciency

In this chapter so far, we have learnt through heuristic arguments that coding efﬁciency is

substantially improved when the code has a variable length. It makes economical sense,

indeed, to use short codewords for the most frequently used symbols, and keep the

longer codewords for the least frequently used ones, which is globally (but not strictly)

the principle of the old Morse code. We must now establish some rules that assign the

most adequate codeword length to each of the source symbols, with the purpose of

achieving a code with optimal efﬁciency.

Consider a basic example. Assume a source with ﬁve symbols, called A, B, C, D, and

E, with the associated probabilities shown below:

x = ABCDE

p(x) = 0.05 0.20.05 0.40.3

8.5 Optimizing coding efﬁciency 139

0.4

0.6

0.3

0.2

0.1

0.05

Codewords

110

1110

1111

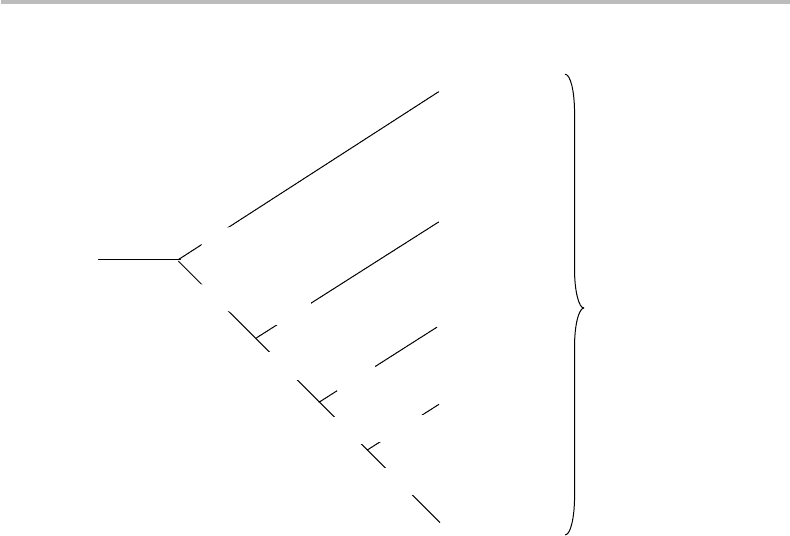
Figure 8.1 Coding tree for the source x = {A, B, C, D, E} with associated probability

distribution p(x) = {0.05, 0.2, 0.05, 0.4, 0.3}.

This source entropy is easily calculated to be H = 1.946 bit/symbol. One method of

assigning a code to each of these symbols is to draw a logical coding tree,asshownin

Figs. 8.1 and 8.2.

The two ﬁgures show that each leaf of the coding tree represents a unique codeword. In

both ﬁgures, the symbols shown at the right are placed in decreasing order of probability.

The coding tree thus assigns each codeword according to successive choices between

0 and 1 as the branches split up. In Fig. 8.1, for instance, symbol D is assigned the

codeword 0, meaning that the other source symbols, A, C, B, and E, should be assigned

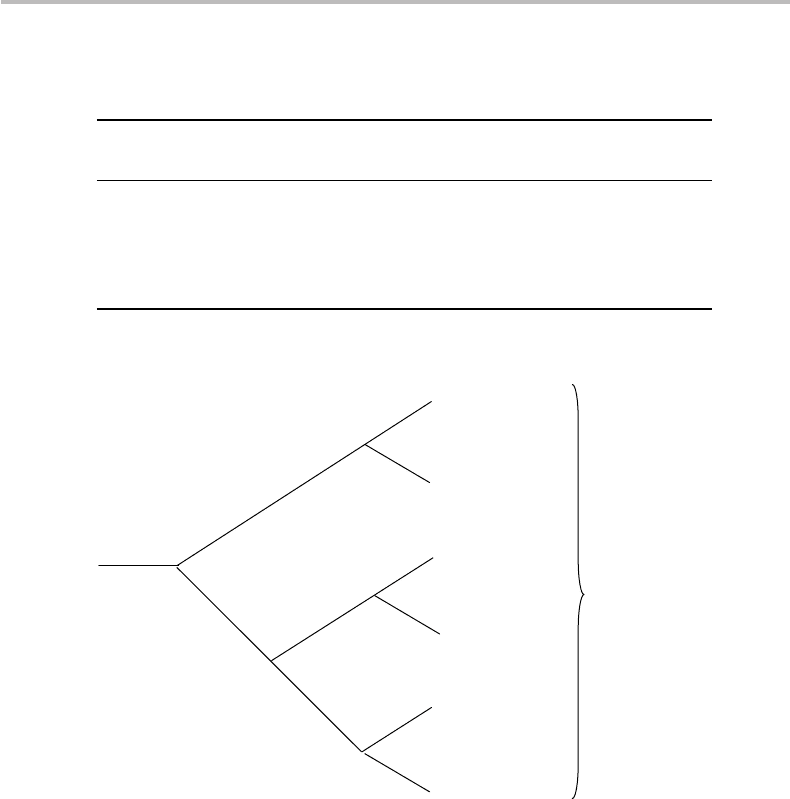
codewords beginning with a 1, and so on. Alternatively (Fig. 8.2), we can assign 0

as the leftmost codeword bit of symbols D, and E, and 1 to all others, and so on. It

is straightforward to calculate the mean codeword length from Eq. (8.4), which gives

L = 2.0 bit/symbol and L = 2.3 bit/symbol, for the two coding trees, respectively.

The coding efﬁciencies are found to be 97.3% and 84.6%, respectively, showing that

the ﬁrst code (Fig. 8.1) is much closer to optimality that the second code (Fig. 8.2). In the

last case, the efﬁciency is relatively low because we have chosen a minimum codeword

length of 2 bits, as opposed to one bit in the ﬁrst case.

In these examples, the choice of codewords (not codeword lengths) seemed to be

arbitrary, but in fact such a choice obeyed some implicit rules.

First, different symbols should be assigned to strictly different codewords. In this

case, the code is said to be nonsingular.

Second (and as previously seen), the code should be uniquely decodable, meaning that

an uninterrupted string of codewords leads to only one and strictly one symbol-sequence

140 Information coding

Table 8.4 Different types of codes for a 5-ary source example made of a binary codeword

alphabet.

Nonsingular, not Uniquely decodable,

Source Singular uniquely decodable not preﬁx Preﬁx

A 00 0 101 101

B 01 1 1011 100

C 10 01 110 110

D 00 10 1101 00

E 10 11 10110 01

0.4

0.2

0.05

Codewords

100

110

111

0.3

0.05

101

Dummy

Figure 8.2 Alternative coding tree for the source in Fig. 8.1.

interpretation. Indeed, consider the code sequence 1101110010 . . . made from a string

of codewords from the code in Fig. 8.1. Scanning from left to right, since 1 and 11 are not

codewords, the ﬁrst matching codeword is 110, or symbol B. The same analysis continues

until we ﬁnd the meaning BADE. The code is, thus, uniquely decodable. We also note

that under this last condition, no codeword represents the beginning bits or preﬁx of

another codeword. This means that the codeword can be instantaneously interpreted

after reading a certain number of bits (this number being known from the identiﬁed

preﬁx), without having to look at the codeword coming next in the sequence. For this

reason, such codes are called preﬁx codes or instantaneous codes. Note that a code

may be uniquely decodable without being of the preﬁx or instantaneous type. Table 8.4

shows examples of singular codes, nonsingular but nonuniquely decodable, uniquely

8.5 Optimizing coding efﬁciency 141

00 01 02

10 11 12

01 20 1 2

200 201 202

120

210 211 212

120

120 120 120

2200 2201 2202 2210 2211 2212

22200

22222

22211

2221222210

120

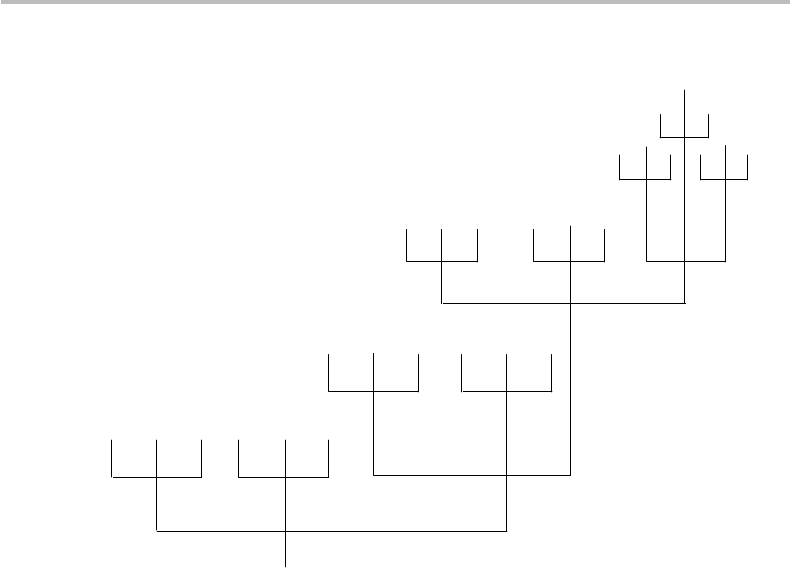
Figure 8.3 Coding tree for A–Z letter source, using ternary codewords (see also Table 8.3).

decodable but not preﬁx, and preﬁx, in the case of a 5-ary code alphabet made of ﬁve

different binary codewords.

We shall now use the coding-tree method to see if we might improve the cod-

ing efﬁciency of the A–Z English-character source, using a ternary alphabet with

variable size (case (iv) in Section 8.4). Figure 8.3 shows a possible coding tree

for a 27-symbol source (26 letters, plus a dummy). The method consists of assign-

ing the ﬁrst group of 2-bit codewords (00, 01, 02, 10, 11, 12) to the ﬁrst six

most frequent characters, then the second group of 3-bit codewords (200, 201,

202, 210, 211, 212) to the following six most frequent characters, and so on,

until all attributions are exhausted (except for a dummy 22222 codeword, which is

never used). The codeword length corresponding to this character–codeword map-

ping is shown in Table 8.3 in Column 8 as l



(x). Column 9 of Table 8.3 details

the calculation of the mean codeword length L



. The result is L



= 2.744 trit/

symbol, which corresponds to a coding efﬁciency of η = H

/L = 96.23%. This coding

efﬁciency is far greater than any efﬁciency obtained so far with ﬁxed and variable-length

codes for the English A–Z character source.

What we have learnt from the above examples is that there exist many possibilities

for assigning variable-length codewords to a given symbol source. Also, we have seen

that the coding tree can be used as a tool towards generating codes with shorter mean

codeword length. We must now formalize our approach, in order to determine the

shortest mean codeword length achievable for any given source, and a method of ﬁnding

the corresponding optimal code, which is described next.

142 Information coding

8.6 Shannon’s source-coding theorem

In this section, we address the following question:

Given a symbol source, what is the smallest mean codeword length achievable?

The answer is provided by a relatively simple demonstration. Let H

(X ) be the entropy

of a M-ary source X =

{

}

with codeword lengths l(x) and corresponding probability

p(x). The mean codeword length is L(X ) =



l(x) p(x). We then estimate the difference

 = L(X) − H

(X ) according to:

 = L(X) − H

(X )



x∈X

l(x) p(x)+



x∈X

p(x)log

p(x) (8.5)



x∈X

p(x)[l(x) +log

p(x)]

≡l + log

p

A sufﬁcient (but not necessary) condition for the difference  to vanish is that each l(x)

takes the speciﬁc value l

∗

(x), as deﬁned by

∗

(x) =−log

p(x). (8.6)

The above result means that if the codeword length l(x) of symbol x is chosen to be

speciﬁcally equal to l

∗

(x) =−log

p(x), then  = 0 and the mean codeword length

L equals the source entropy H

. We note that this optimal length l

∗

(x) represents

the information contained in the symbol x, which was deﬁned in Chapter 3 as being

I (x) =−log

p(x), and which is a measure of the symbol uncertainty. Thus, the

codeword lengths are short for symbols with less information (more frequent, or less

uncertain) and are long for symbols with more information (less frequent, or more

uncertain). Since the codeword lengths must be integer numbers, the optimal condi-

tion l

∗

(x) =−log

p(x) can only be approximately satisﬁed in the general case. The

codeword lengths must then be chosen as the integer number greater than but closest to

∗

(x).

The above demonstration does not prove that the choice of codeword length l

∗

(x)

minimizes the mean codeword length L. We don’t know, either, if the difference 

is positive or negative in the general case. To establish both properties, we must use

the so-called Kraft–McMillan inequality, which is demonstrated in Appendix F. This

inequality, which applies to preﬁx codes,

states



x∈X

−l(x)

≤ 1. (8.7)

Let’s prove ﬁrst that l

∗

(x) is the minimum mean codeword length. For this, we apply

the Lagrange-multipliers method, which we have already used in Chapters 4 and 6 to

As it turns out, the Kraft inequality also applies to the greater class of uniquely decodable codes (McMillan

inequality), hence the name Kraft–McMillan inequality.

8.6 Shannon’s source-coding theorem 143

maximize the entropy of discrete and continuous sources. To recall, this method makes

it possible to ﬁnd the function l

opt

(x) for which any function L(l) is minimized (or

maximized), given the constraint that C(l) = u, where L , C are any derivable functions

of l and u is a constant. Formally, one ﬁrst deﬁnes:

J (l) = L(l) +λC(l), (8.8)

where L(l) =



p(x)l(x) and C(l) =



−l(x)

≡



−l(x)lnM

= u. The derivation

of Eq. (8.8) with respect to l(x) leads to

∂ J

∂l(x)

= p(x) − λlM

−l(x)

l(x)lnM. (8.9)

Setting the result in Eq. (8.9) to zero, we obtain the parameter λ, which, with the

constraint, yields the optimum function l

opt

(x):

opt

(x) =−log

p(x) − log

u. (8.10)

Since by deﬁnition u ≤ 1, the smallest codeword-length for any x is given by

∗

(x) =−log

p(x), (8.11)

which we had previously found in Eq. (8.6) to be the function for which L(X) = H (X).

The above demonstration proves that the codeword length distribution l

∗

(x) yields the

shortest mean codeword length L(X). We can now prove that the source entropy H (X)

represents an absolute lower bound for L(X). Indeed,

 = L(X) − H

(X )



x∈X

p(x)[l(x) +log

p(x)]



x∈X

p(x)[log

p(x) − log

−l(x)

]



x∈X

p(x)[log

p(x) − log

(AM

−l(x)

) + log

A] (8.12)



x∈X

p(x)log



p(x)

−l(x)





x∈X

p(x)log

≡ D( pAM

−l(x)

) + log

In the above development, we have introduced the constant A = 1/



−l(x)

, which

makes the function AM

−l(x)

a probability distribution. Thus D( pAM

−l(x)

)isa

Kullback–Leibler distance, which, from Chapter 5, we know to be always nonnega-

tive. Because of the Kraft–McMillan inequality, we also have A ≥ 1, or log

A ≥ 0.

The conclusion is that we always have  ≥ 0, which leads to Shannon’s source-coding

Namely, λ = 1/(u ln M ), which comes from substituting the result M

−l(x)

= p(x)/(λ ln M) into the con-

straint C (l) =



−l(x)

= u, and using



p(x) = 1. This leads to p(x ) = M

−l(x)

/u, from which we

obtain l(x ) ≡ l

opt

(x ) =−log

p(x) −log

144 Information coding

theorem:

L(X ) ≥ H

(X ). (8.13)

The theorem translates into the following:

The mean codeword length cannot be shorter than the source entropy: equality is achieved when

the codeword lengths are chosen such that l(x) = l

∗

(x ) =−log

p(x).

In the general case, there is no reason for l

∗

(x) to be an integer. In this case, a

compromise is to take the smallest integer value greater than or equal to l

∗

(x), which

is noted



∗

(x)



. Such a realistic code assignment is called a Shannon code, which

is also known as Shannon–Fano code. We, thus, have l

∗

(x) =



∗

(x)



− ε(x), with

0 ≤ ε(x) < 1. This relation gives the realistic minimal value of the mean codeword

length, which we shall call here L

∗∗

, and deﬁne according to:

∗∗

(X ) =



x∈X

p(x)l

∗

(x)



x∈X

p(x)

[

∗

(x) +ε(x)

]

(8.14)

≡ H

(X ) +ε

Since 0 ≤ε

< 1, it immediately follows that

(X ) ≤ L

∗∗

(X ) < H

(X ) +1, (8.15)

which represents another fundamental property of minimal-length codes (or Shannon–

Fano codes). The result can be restated as follows:

There exists a code whose mean codeword length falls into the interval

[

, H

+ 1

]

;itisequal

to the source entropy H

if the distribution l

∗

=−log

p has integer values (dyadic source).

This source-coding theorem was the ﬁrst to be established by Shannon, which explains

its other appellation of Shannon’s ﬁrst theorem.

By deﬁnition, we call redundancy the difference ρ = L − H . We call ρ

bound

the upper

bound of the redundancy, i.e., ρ<ρ

bound

is always satisﬁed. The Shannon–Fano code

redundancy bound is therefore ρ

bound

= 1 bit/symbol, which means that in the general

case, L

∗∗

< H + 1, consistently with Eq. (8.15). In the speciﬁc case of dyadic sources

∗

=−log

p is an integer for all x), we have L

∗

= H , and ρ = 0 bit/symbol.

We have seen from the preceding demonstration of Shannon’s source-coding theorem,

that there exists an optimum codeword-length assignment (l

∗

(x), or more generally,

∗∗

(x)) for which the mean codeword length is minimized. What if we were to use a

different assignment? Assume that this assignment takes the form

l(x) =−log

q(x),

where q(x) is an arbitrary distribution. It follows from this assignment that the mean

codeword length becomes:

L(X ) =



x∈X

p(x)

l(x)



x∈X

p(x)

log

q(x)

8.6 Shannon’s source-coding theorem 145



x∈X

p(x)



log

q(x)

+ ε(x)





x∈X

p(x)



log

p(x)

q(x) p(x)

+ ε(x)



(8.16)



x∈X

p(x)



log

p(x)

q(x)



−



x∈X

p(x)[log

p(x)] +ε

≡ D( pq) + H

(X ) +ε

Since 0 ≤ε

< 1, it immediately follows from the above result that

(X ) + D( p

q ) ≤

L(X ) (8.17)

< H

(X ) + D( p

q ) + 1.

The result illustrates that a “wrong” choice of probability distribution results in

a “penalty” of D(p q) for the smallest mean codeword length, which shifts

the boundary interval according to

L(X ) ∈

[

(X ) + D, H

(x) + D + 1

]

. Such a

penalty can, however, be small, and a “wrong” probability distribution can, in

fact, yield a mean codeword length

L(X ) smaller than L

∗∗

(X ). This fact will be

proven in Chapter 9, which concerns optimal coding, and speciﬁcally Huffman

codes.

Since the above properties apply to any type of M-ary coding, we may wonder (inde-

pendently of technological considerations for representing, acquiring, and displaying

symbols) whether a speciﬁc choice of M could also lead to an absolute minimum for the

expected length L(X). Could the binary system be optimal in this respect, considering

the fact that the codewords have the longest possible lengths? A simple example with

the English-character source (X =

{

A − Z

}

, 1982 survey, see Chapter 4) provides a ﬁrst

clue. Table 8.5 shows the mean codeword lengths L

∗∗

(X ) for various multi-level codes:

binary, ternary, quaternary, and 26-ary, with the details of their respective code-length

assignments.

We observe from Table 8.5 that the binary code has the smallest mean codeword length

relative to the source entropy, i.e., L

∗∗

(x) =4.577 bit/symbol, yielding the highest coding

efﬁciency of η = 91.42%. This result is better than the value of η = 83.70% found for

a ﬁxed-length binary code with 5 bit/symbol (such as ASCII reduced to lower-case

or upper-case letters). Moving from binary to ternary is seen to decrease the coding

efﬁciency to η = 84.37%. The efﬁciency increases somewhat with the quaternary code

(η = 84.63%.), but apart from such small irregularities due to the integer truncation

effect, it decreases with increasing M.ForM = 26, the efﬁciency has dropped to

η = 72.63%. This last result is substantially lower than the value of η = 89.0%, which

we found earlier for ﬁxed-length, 26-ary coding having one character/symbol. The

conclusion of this exercise is that the Shannon code does not necessary yield better

efﬁciencies than a ﬁxed-length code, against all expectations. In the example of the

English-character source, the Shannon code is better with binary codewords, but it is

146 Information coding

Table 8.5 Shannon codes for the English-character source, using binary, ternary, quaternary, and 26-ary codewords.

Binary coding Ternary coding

Ideal Real Mean Ideal Real Mean

CW CW CW CW CW CW

length length length length length length

xp(x) p log

(p) l

∗

(x ) l

∗∗

(x ) l

∗∗

(x )p(x) p log

(x ) l

∗

(x ) l

∗∗

(x ) l

∗∗

(x )p(x)

E 0.127 0.378 2.9771 3 0.381 0.239 1.8783 2 0.254

T 0.091 0.314 3.4623 4 0.363 0.198 2.1845 3 0.272

A 0.082 0.295 3.6126 4 0.327 0.186 2.2793 3 0.245

O 0.075 0.280 3.7413 4 0.299 0.177 2.3605 3 0.224

I 0.070 0.268 3.8408 4 0.279 0.169 2.4233 3 0.209

N 0.067 0.261 3.904 4 0.267 0.165 2.4632 3 0.200

S 0.063 0.251 3.9928 4 0.251 0.158 2.5192 3 0.188

H 0.061 0.246 4.0394 5 0.304 0.155 2.5486 3 0.182

R 0.060 0.243 4.0632 5 0.299 0.153 2.5636 3 0.179

D 0.043 0.195 4.5438 5 0.214 0.123 2.8668 3 0.129

L 0.040 0.185 4.6482 5 0.199 0.117 2.9327 3 0.120

C 0.028 0.144 5.1628 6 0.167 0.091 3.2573 4 0.112

U 0.028 0.144 5.1628 6 0.167 0.091 3.2573 4 0.112

M 0.024 0.129 5.3851 6 0.144 0.081 3.3976 4 0.096

W 0.024 0.129 5.3851 6 0.144 0.081 3.3976 4 0.096

F 0.022 0.121 5.5107 6 0.132 0.076 3.4768 4 0.088

G 0.020 0.113 5.6482 6 0.120 0.071 3.5636 4 0.080

Y 0.020 0.113 5.6482 6 0.120 0.071 3.5636 4 0.080

P 0.019 0.108 5.7222 6 0.114 0.068 3.6103 4 0.076

B 0.015 0.091 6.0632 7 0.105 0.057 3.8255 4 0.060

V 0.010 0.066 6.6482 7 0.070 0.042 4.1945 5 0.050

K 0.008 0.056 6.9701 7 0.056 0.035 4.3976 5 0.040

J 0.002 0.018 8.9701 9 0.018 0.011 5.6595 6 0.012

X 0.002 0.018 8.9701 9 0.018 0.011 5.6595 6 0.012

Q 0.001 0.010 9.9701 10 0.010 0.006 6.2904 7 0.007

Z 0.001 0.010 9.9701 10 0.010 0.006 6.2904 7 0.007



1.000

Entropy H

= 4.185 L

∗∗

= 4.577 H

= 2.640 L

∗∗

= 3.19

bit/symbol bit/symbol trit/symbol trit/symbol

(source) (code) (source) (code)

Coding 91.42% 84.37%

efﬁciency

Quaternary coding 26-ary coding

Ideal Real Mean Ideal Real Mean

CW CW CW CW CW CW

length length length length length length

xp(x) p log

(p) l

∗

(x ) l

∗∗

(x ) l

∗∗

(x )p(x) p log

(x ) l

∗

(x ) l

∗∗

(x ) l

∗∗

(x )p(x)

E 0.127 0.189 1.4885 2 0.254 0.080 0.6334 1 0.127

T 0.091 0.157 1.7312 2 0.181 0.067 0.7366 1 0.091

A 0.082 0.148 1.8063 2 0.164 0.063 0.7686 1 0.082

(cont.)