Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


Appendix N (Chapter 16) Pauli matrices,
rotations, and unitary operators
In this appendix, I provide further conceptual background concerning Pauli matrices.
It is shown that Pauli matrices make it possible to define any 2 × 2 unitary matrix
U (namely, satisfying the property U
+
U = I , where the upper symbol (
+
) stands for
Hermitian conjugation, and I is the identity matrix. The different results or theorems
obtained in this appendix will be usefully applied to other chapters.
Recall first the definitions of the four Pauli matrices:
I ≡ σ
0
=
10
01
X ≡ σ
x
= σ
1
=
01
10
Y ≡ σ
y
= σ
2
=
0 −i
i
0
Z ≡ σ
z
= σ
3
=
10
0 −1
.
(N1)
Note that the different notations σ
0,1,2,3
, σ
0,x,y,z
, and I, X, Y, Z are equivalent. We
progress in several steps, which recall the properties of unitary operators, their complex-
exponential representation, and, finally, the representation of unitary operators through
rotations on the Bloch sphere.
Hermitian conjugation and unitary matrices
Given an operator A, whose matrix representation is characterized by the complex coef-
ficients a
ij
,theHermitian conjugate of A, called A
+
, is defined by the coefficients
¯
a
ji
,
corresponding to the complex-conjugate, transposed matrix. By definition, an operator
or matrix is called unitary if it satisfies the property A
+
A = I .
Exponential representation of complex numbers
A complex number z = a + ib has modulus or length |z|=zz
∗
=
√
a
2
+ b
2
. It is pos-
sible to represent a complex number in the form
z =
|
z
|
a
√
a
2
+ b
2
+
i
b
√
a
2
+ b
2
≡
|
z
|
(
cos θ +isinθ
)
,
(N2)
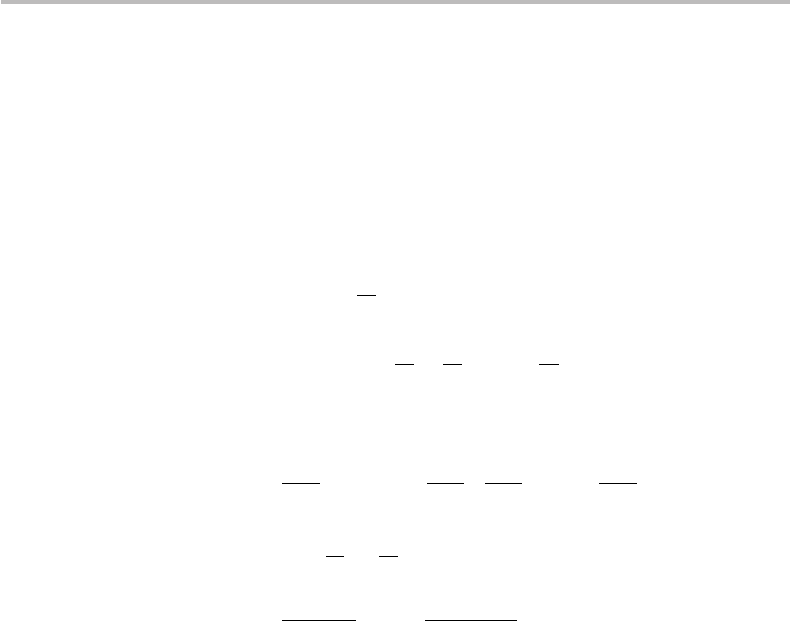
628 Appendix N
where θ = tan
−1
(b/a) is the argument of z. One may also write:
z =
|
z
|
(
cos θ +isinθ
)
≡
|
z
|
e
iθ
, (N3)
where
e
iθ
= cos θ +isinθ is a complex number called an imaginary exponential.
Such notation is justified if one considers the definition of the real exponential
exp(x) = e
x
:
e
x
=
∞
n=0
x
n
n!
= 1 + x +
x
2
2!
+
x
3
3!
+···+
x
n
n!
+···
(N4)
Substituting x = iθ into Eq. (N4) yields
e
iθ
=
∞
n=0
(iθ)
n
n!
= 1 + iθ +
(iθ)
2
2!
+
(iθ)
3
3!
+···+
(iθ)
n
n!
+···
= 1 +iθ −
θ
2
2!
− i
θ
3
3!
+···
=
∞
n=0
(−1)
n
θ
2n
(2n)!
+ i
∞
n=0
(−1)
n
θ
2n+1
(2n + 1)!
≡ cos θ + isinθ,
(N5)
where the two series corresponding to the real and imaginary parts of
e
iθ
have been
substituted with their exact function definitions cos θ and sin θ , respectively. Noteworthy
are the two identities
exp(iπ) =−1, (N6)
exp(iπ/2) = i. (N7)
Exponential operator
Assume an operator A satisfying the property A
2
= I . We then define the exponential
operator exp(iAθ) according to
exp(i Aθ) = cos(θ )I + isin(θ )A. (N8)
Note in Eq. (N8) that the real part of the exponential involves the operator I and
the imaginary part involves the operator A. One proves the above development by
substituting the argument x = iAθ in the series expansion in Eq. (N4) and using the

Pauli matrices, rotations, and unitary operators 629
property A
2
= I :
e
iAθ
=
∞
n=0
(iAθ )
n
n!
= I + iAθ +
(iAθ )
2
2!
+
(iAθ )
3
3!
+···+
(iAθ )
n
n!
+···
= I + iAθ −
θ
2
I
2!
− i
θ
3
A
3!
+···
=
∞
n=0
(−1)
n
θ
2n
(2n)!
I + i
∞
n=0
(−1)
n
θ
2n+1
(2n + 1)!
A
≡ cos(θ )I + isin(θ) A
(N9)
(in the above, the two series expansions are recognized to correspond to the functions
cos θ and sin θ , respectively).
Rotation operators
We now have the mathematical tools to introduce a new class of unitary operators
generated by the three Pauli matrices X, Y, Z , and called rotation operators. Such
operators are defined according to:
R
x
(γ ) =
e
−i
γ
2
X
=
e
−i
γ
2
σ
1
R
y
(γ ) =
e
−i
γ
2
Y
=
e
−i
γ
2
σ
2
R
z
(γ ) =
e
−i
γ
2
Z
=
e
−i
γ
2
σ
3
.
(N10)
The above exponential-operator definitions are relevant, since Pauli matrices satisfy the
condition X
2
= Y
2
= Z
2
= σ
2
i
= 1. Substituting the definitions in Eqs. (N1) and (N8)
into Eq. (N10) yields (as easily checked):
R
x
(γ ) = cos
γ
2
I − isin
γ
2
X =
cos
γ
2
−isin
γ
2
−isin
γ
2
cos
γ
2
R
y
(γ ) = cos
γ
2
I − isin
γ
2
Y =
cos
γ
2
−sin
γ
2
sin
γ
2
cos
γ
2
R
z
(γ ) = cos
γ
2
I − isin
γ
2
Z =
exp
#
−i
γ
2
$
0
0exp
#
i
γ
2
$
.
(N11)
630 Appendix N
0
1
θ
q
ϕ
x
y
z
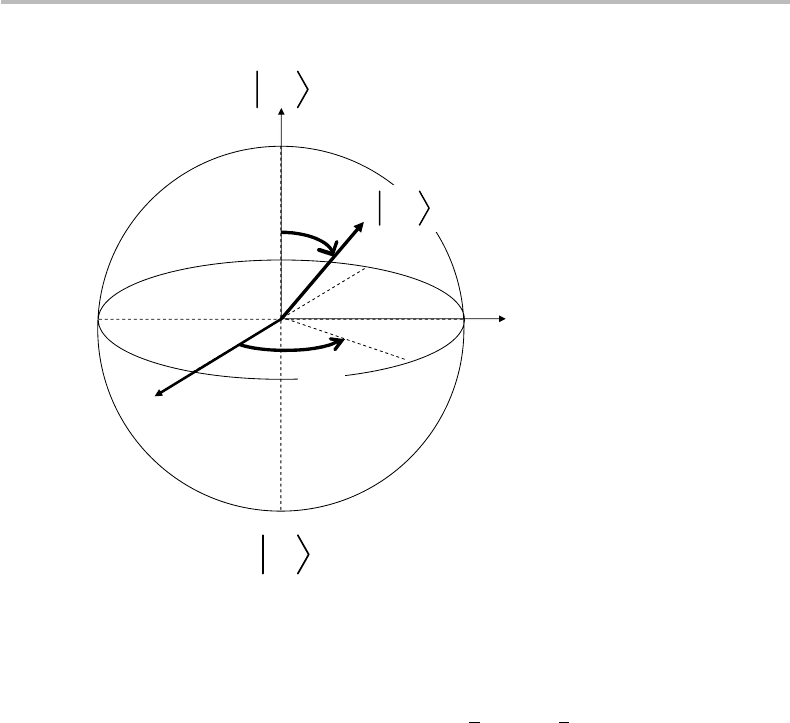
Figure N1 Qubit represented as point of coordinates (θ,ϕ) on Bloch sphere.
I shall now interpret the effect of the three above rotation operators on qubits. As we
have seen from the main text, the general definition of a qubit |q is
|q=α|0+β|1=cos
θ
2
|0+sin
θ
2
e
iϕ
|1. (N12)
The above definition shows that any qubit can be represented by a single point of
angular coordinates (θ,ϕ) on the surface of the Bloch sphere (with θ = 0 → π and
ϕ = 0 → 2π ), which is show in Fig. N1 for convenience.
It is left as an exercise to show that the three operators R
k
(γ )(k = x, y, z) rotate the
qubit by an angle γ about the axis k, in the counterclockwise direction.
Consider next a more general form of the rotation operator. First, we define the Pauli
vector in the Cartesian reference frame ( x, y, z)) according to
σ = σ
1
x + σ
2
y + σ
3
z
= (σ
1
,σ
2
,σ
3
).
(N13)
Given a unitary vector n = (n
x
, n
y
, n
z
), the scalar product n · σ corresponds to the
matrix operator defined by U = n · σ = n
x
σ
1
+ n
y
σ
2
+ n
z
σ
3
. It is easily established
that U is unitary or U
2
= I . Indeed, we have
U
2
= UU
= (n
x
σ
1
+ n
y
σ
2
+ n
z
σ
3
)(n
x
σ
1
+ n
y
σ
2
+ n
z
σ
3
)
=
n
2
x
+ n
2
y
+ n
2
z
I + n
x
n
y
(σ
1
σ
2
+ σ
2
σ
1
) + n
y
n
z
(σ
2
σ
3
+ σ
3
σ
2
)n
z
n
x
(σ
3
σ
1
+ σ
1
σ
3
)
= I. (N14)

Pauli matrices, rotations, and unitary operators 631
In the above result, we have applied the property in Eq. (16.19) from the text, namely
σ
i
σ
j
=−σ
j
σ
i
for i = j and our assumption that n is unitary (n
2
x
+ n
2
y
+ n
2
z
= 1). Since
U
2
= 1, the exponential-operator definition in Eq. (N9) is valid for the operator U , and
we have, for any real θ:
exp(iU θ ) = I cos θ + iU sin θ
↔
exp[i( n · σ )θ] = I cos θ + i( n · σ )sinθ.
(N15)
We recognize in this result a more general expression from which the elementary rotation
operators R
k
(γ )(k = x, y, z) defined in Eq. (N10) can be derived, i.e., by setting n = x,
n = y,or n = z with θ =−γ/2. The general expression corresponds to a qubit rotation
of (counterclockwise) angle γ about the axis defined by the unit vector n = (n
x
, n
y
, n
z
).
Since the result of any 2 × 2 unitary transformation A is to move a qubit on the
surface of the Bloch sphere, there exists a unique rotation associated with such a move
(like taking a direct flight from city to city on the Earth). This unique rotation is defined
through the operator exp[i( n · σ )θ] = A (within an unobservable phase factor). We can
make this operator more explicit, by developing the definition in Eq. (N15), according
to
exp[i( n · σ )θ] = I cos θ +i( n · σ )sinθ
= σ
0
cos θ +isinθ(n
x
σ
1
+ n
y
σ
2
+ n
z
σ
3
)
(N16)
or
A ≡
e
iδ
exp[i( n · σ )θ]
≡
3
i=0
µ
i
σ
i
.
(N17)
where µ
i
are complex numbers defined by
µ
0
= cos θ,µ
1
= in
x
sin θ,µ
2
= in
y
sin θ,µ
3
= in
z
sin θ, (N18)
which, in particular, satisfy
i
|
µ
i
|
2
= 1. To summarize this result, any 2 × 2 unitary
transformation, or rotation on the Bloch sphere, can be expressed as a linear com-
plex expansion of Pauli matrices. It is left as an elementary exercise to determine the
parameters n,θ associated with any unitary transformation A.
Euler’s theorem
This theorem states that every 2 × 2 unitary matrix U can be expressed from the two
rotation operators R
y
, R
z
and a set of four real numbers α, β, γ , δ, according to the
product:
U =
e
iδ
R
z
(α)R
y
(β)R
z
(γ ). (N19)

632 Appendix N
To show this, we first substitute the corresponding definitions of R
y
, R
z
from Eq. (N11)
to obtain:
U =
e
iδ
e
−i
α+γ
2
cos
β
2
−
e
−i
α−γ
2
sin
β
2
e
i
α−γ
2
sin
β
2
e
i
α+γ
2
cos
β
2
. (N20)
It is left as an exercise to prove that the unitary condition U
+
U = 1 is both necessary
and sufficient for the above matrix coefficients to represent any unitary matrix U .
Euler’s theorem, as defined in Eq. (N19), is referred to as Z-Y decomposition of
rotations. In fact Z-X decomposition, according to U =
e
iδ
R
z
(α)R
x
(β)R
z
(γ ), is also
possible, as well as any decomposition involving two different Pauli operators. Most
generally, given any two nonparallel unitary vectors n, m
U =
e
iδ
R
n
(α)R
m
(β)R
n
(γ ), (N21)
where R
p
(θ) = exp[i( p · σ )θ] is the rotation operator of angle θ about the axis defined
by the unitary vector p.
Decomposition of 2 × 2 unitary matrices
A general property stemming from Euler’s theorem is that any 2 ×2 unitary matrix can
be decomposed according to
U =
e
iδ
AXBXC, (N22)
where A, B, C are 2 × 2 unitary matrices satisfying ABC = I and X = σ
1
.
To prove this property, we must find at least one set of three matrices A, B, C that
satisfies ABC = I and correspond to the unique decomposition of U in Eq. (N22).
Assume heuristically, for instance,
A = R
z
(2ψ)R
y
(−2χ)
B = R
y
(2χ)R
z
(2ω)
C = R
z
(2φ),
(N23)
where φ,χ,ψ are rotation angles to be determined (the factor of two will lighten the
calculations). It is clear that Eq. (N23) satisfies the condition ABC = I ,or
ABC = R
z
(2ψ)R
y
(−2χ)R
y
(2χ)R
z
(2ω)R
z
(2φ)
≡ R
z
(2ψ)R
z
(2ω)R
z
(2φ)
= I,
(N24)
if we impose the angle condition
ψ +ω + φ = 0. (N25)

Pauli matrices, rotations, and unitary operators 633
We shall now develop the product AXBXC to obtain
AXBXC = AXBXR
z
(2φ)
= AXB
01
10
e
−iφ
0
0e
iφ
= AXB
0e
iφ
e
−iφ
0
= AXR
y
(2χ)R
z
(2ω)
0e
iφ
e
−iφ
0
= AXR
y
(2χ)
e
−iω
0
0e
iω
0e
iφ
e
−iφ
0
= AXR
y
(2χ)
0e
−i(ω−ϕ)
e
i(ω−ϕ)
0
= AX
cos χ −sin χ
sin χ cos χ
0e
−i(ω−ϕ)
e
i(ω−ϕ)
0
= AX
−sin χ
e
i(ω−ϕ)
cos χ
e
−i(ω−ϕ)
cos χ
e
i(ω−ϕ)
sin χ
e
−i(ω−ϕ)
= A
01
10
−sin χ
e
i(ω−ϕ)
cos χ
e
−i(ω−ϕ)
cos χ
e
i(ω−ϕ)
sin χ
e
−i(ω−ϕ)
= A
cos χ
e
i(ω−ϕ)
sin χ
e
−i(ω−ϕ)
−sin χ
e
i(ω−ϕ)
cos χe
−i(ω−ϕ)
= R
z
(2ψ)R
y
(−2χ)
cos χ
e
i(ω−ϕ)
sin χ
e
−i(ω−ϕ)
−sin χ
e
i(ω−ϕ)
cos χ
e
−i(ω−ϕ)
= R
z
(2ψ)
cos χ sin χ
−sin χ cos χ
cos χ
e
i(ω−ϕ)
sin χ
e
−i(ω−ϕ)
−sin χ
e
i(ω−ϕ)
cos χe
−i(ω−ϕ)
= R
z
(2ψ)
[cos
2
χ −cos
2
χ]
e
i(ω−ϕ)
2 cos χ sin χ
e
−i(ω−ϕ)
−2 cos χ sin χ
e
i(ω−ϕ)
[cos
2
χ −cos
2
χ]
e
−i(ω−ϕ)
= R
z
(2ψ)
cos 2χe
i(ω−ϕ)
sin 2χe
−i(ω−ϕ)
−sin 2χe
i(ω−ϕ)
cos 2χe
−i(ω−ϕ)
=
e
−iψ
0
0
e
iψ
cos 2χ
e
i(ω−ϕ)
sin 2χ
e
−i(ω−ϕ)
−sin 2χ
e
i(ω−ϕ)
cos 2χ
e
−i(ω−ϕ)
=
cos 2χ
e
i(ω−ϕ−ψ)
sin 2χ
e
−i(ω−ϕ+ψ)
−sin 2χ
e
i(ω−ϕ+ψ)
cos 2χ
e
−i(ω−ϕ−ψ)
≡
cos 2χ
e
−2i(ϕ+ψ)
sin 2χ
e
2iϕ
−sin 2χ
e
−2iϕ
cos 2χ
e
2i(ϕ+ψ)
.
(N26)

634 Appendix N
Identifying this result with the definition in Eq. (N20), we obtain
e
−i
α+γ
2
cos
β
2
−
e
−i
α−γ
2
sin
β
2
e
i
α−γ
2
sin
β
2
e
i
α+γ
2
cos
β
2
=
3
cos 2χ
e
−2i(φ+ψ)
sin 2χ
e
2iφ
−sin 2χ
e
−2iφ
cos 2χ
e
2i(φ+ψ)
4
(N27)
and, thus,
2χ =−
β
2
, 2φ + 2ψ =
α + γ
2
=−2ω, −2φ =
α − γ
2
↔
2χ =−
β
2
, 2ψ = α, 2ω =−
α + γ
2
, 2φ =
γ − α
2
.
(N28)
The three unitary operators are then fully defined according to
A = R
z
(α)R
y
β
2
B = R
y
−
β
2
R
z
−
α + γ
2
C = R
z
γ − α
2
.
(N29)
Commutation properties of rotation operators
Two rotation operators R
i
(θ), R
j
(ϕ) do not commute except when i = j.Itisleftasan
easy exercise to verify that
[R
i
(2θ), R
j
(2ϕ)] =−2iε
ijk
σ
k
sin θ sin ϕ. (N30)
Consider, for instance, the triple rotation A = R
i
(−θ)R
j
(ϕ)R
i
(θ), with i = j. We would
intuitively think that the last rotation R
i
(−θ) cancels the effect of the first rotation R
i
(θ)
and, therefore, that A = R
j
(ϕ) but, as we shall see, this is not the case. Indeed:
A = R
i
(−θ)R
j
(ϕ)R
i
(θ)
= R
i
(−θ){R
i
(θ)R
j
(ϕ) +[R
j
(ϕ), R
i
(θ)]}
= R
i
(−θ)R
i
(θ)R
j
(ϕ) + R
i
(−θ)[R
j
(ϕ), R
i
(θ)]
= R
j
(ϕ) −2iε
ijk
R
i
(−θ)σ
k
,
(N31)
which proves that, except for i = j (ε
ijk
= 0), in the general case A = R
j
(ϕ).
It is also straightforward to show that the commutation of the rotation operators with
the Pauli matrices satisfy
[R
i
(2θ),σ
j
] = 2iε
ijk
sin θσ
k
. (N32)
This result expresses the fact that the two operators R
i
(2θ),σ
j
do not commute, except
in the specific cases i = j (ε
iik
= 0) and 2θ = 0, 2π (R
i
(0) = R
i
(2π) = I ).

Appendix O (Chapter 17) Heisenberg
uncertainty principle
In this appendix, I provide a demonstration of the Heisenberg uncertainty principle.
1
According to this principle, the uncertainties A,B associated with two observables
A, B, measured in the state |ψ, must satisfy the inequality:
AB ≥
1
2
|ψ|[ A, B]|ψ|. (O1)
To prove Eq. (O1), define
|ϕ=
(
A +iλB
)
|ψ, (O2)
where λ is a real parameter. We then obtain
ϕ|ϕ=ψ|(A +
i
λB)
+
(A +
i
λB)|ψ
=ψ|( A
+
−
i
λB
+
)(A +
i
λB)|ψ
=ψ|A
+
A|ψ+
i
λψ|(A
+
B − B
+
A)|ψ+ψ|B
+
B|ψ
≡ψ|A
2
|ψ+
i
λψ|[A, B]|ψ+λ
2
ψ|B
2
|ψ
≥ 0,
(O3)
where we used the commutator definition [A, B] = AB − BA and the fact that the
observables are Hermitian. The property ϕ|ϕ≥0 (with ϕ|ϕ real) is inherent to
the definition of inner product. We also have the property ψ|X
2
|ψ≥0 for any
observable X = A, B and state |ψ, see note. Hence,
i
ψ|
[
A, B
]
|ψ must be real,
with
i
ψ|
[
A, B
]
|ψ=±|ψ|
[
A, B
]
|ψ|, and Eq. (O3) is of the polynomial form
P(λ) = aλ
2
± bλ ≥ c ≥ 0 with real coefficients a, b, c satisfying a, b, c ≥ 0. Since
P(λ) ≥ 0, it can only have zero or one root, which corresponds to a discriminant
δ = b
2
− 4ac ≤ 0. We, thus, have
δ =|ψ|
[
A, B
]
|ψ|
2
− 4ψ |B
2
|ψψ|A
2
|ψ
≤ 0,
(O4)
1
See, for instance: C. Cohen-Tannoudji, B. Diu, and F. Laloe, Quantum Mechanics (Paris: Hermann, 1977),
Vol. 1, pp. 28–7.

636 Appendix O
which can be put in the inequality form:
ψ|A
2
|ψψ|B
2
|ψ≡A
2
B
2
≥
1
4
|ψ|[ A, B]|ψ|
2
.
(O5)
Now define the new observables
˜
A,
˜
B from the previous observables A, B according to
A =
˜
A −ψ|
˜
A|ψ≡
˜
A −
˜
A
B =
˜
B −ψ|
˜
B|ψ ≡
˜
B −
˜
B.
(O6)
It is easily verified that [A, B] = [
˜
A,
˜
B]. Substituting the definitions in Eq. (O6)into
Eq. (O5), we obtain
A
2
B
2
=(
˜
A −
˜
A)
2
(
˜
B −
˜
B)
2
, (O7)
or
˜
A
2
˜
B
2
≥
1
4
|ψ|[
˜
A,
˜
B]|ψ|
2
, (O8)
or
˜
A
˜
B ≥
1
2
|ψ|[
˜
A,
˜
B]|ψ|. (O9)
It is also easily verified that X
2
=
˜
X
2
for any operator X = A, B defined by
Eq. (O6). Hence, we finally obtain the Heisenberg uncertainty relation:
AB ≥
1
2
|ψ|[ A, B]|ψ|. (O10)
Note
The property ψ|X
2
|ψ≥0 for any observable X and state |ψ is shown as follows.
Because X is an observable, there exists an orthonormal or eigenstate base {|λ
i
}, whose
state elements satisfy X |λ
i
=λ
i
|λ
i
, where λ
i
are the corresponding real eigenvalues.
The state |ψ can, thus, be uniquely decomposed into this base with coordinates µ
i
,
according to
|ψ=
i
x
i
|λ
i
.
Hence, we obtain:
ψ|X
2
|ψ=
3
i
¯µ
i
λ
i
|
4
XX
j
µ
j
|λ
j
=
i
j
¯µ
i
µ
j
λ
i
λ
j
δ
ij
=
i
λ
2
i
|µ
i
|
2
≥ 0.
