Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

Arithmetic coding algorithm 607

)()(

xpxp

)(

223

213

123

113

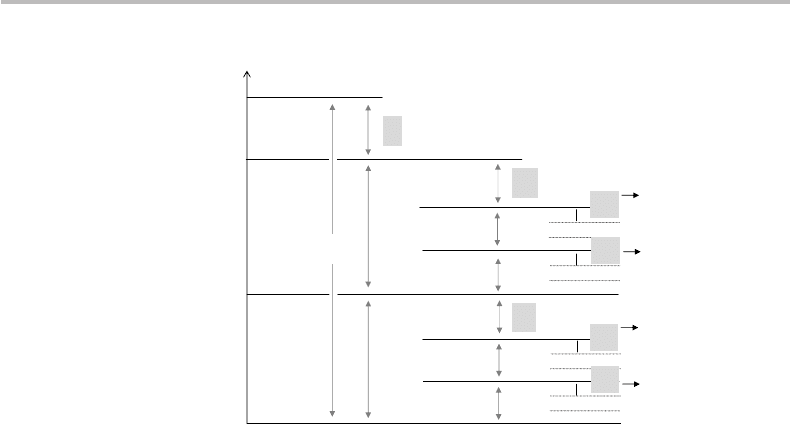
Figure H2 Symbol strings with lengths up to N = 3.

The same results as in Eqs. (H9) and (H10) can be obtained for the interval I

, corre-

sponding to the string x

(Fig. H1), with the argument I

changed into I

Consider next the case of symbol strings with lengths up to N = 3, which correspond

to all the intervals that have been highlighted in Fig. H2.

The strings with lengths N = 3, namely x

, x

, and x

,are

associated with the subintervals I

113

, I

123

, I

213

, and I

223

. We do not need to consider all

of them to prove the general relation that deﬁnes the start and stop values of each of

these subintervals. Take, for instance, I

223

. Looking at Fig. H2, we readily obtain:











u(I

223

) = p(x

) + p(x

)p(x

) + p(x

, x

)p(x

, x

) + p(x

, x

)p(x

, x

)

= p(x

) + p(x

, x

) + p(x

, x

)

[

p(x

, x

) + p(x

, x

)

]

≡ u(I

) + w(I

)



i=1

p(x

, x

)

v(I

223

) = p(x

) + p(x

)p(x

) + p(x

, x

)p(x

, x

) + p(x

, x

)p(x

, x

)

+ p(x

, x

)p(x

, x

)

= p(x

) + p(x

, x

) + p(x

, x

)[p(x

, x

) + p(x

, x

) + p(x

, x

)]

≡ u(I

) + w(I

)



i=1

p(x

, x

(H11)

In this derivation, we used the property p(x

, x

) = w(I

) = v(I

) − u(I

), according

to which the width of the subinterval corresponding to a preceding string sequence x

is equal to the joint probability p(x

, x

) = p(x

)p(x

). We also used the fact that, by

deﬁnition, u(I

) = p(x

) + p(x

, x

608 Appendix H

The previous analysis makes it possible to rewrite Eq. (H11) concerning any three-

symbol string of the type x

(m, n = 1 ...2) in the general form:











u(I

mn3

) = u(I

) + w(I

)



i=1

p(x

, x

)

v(I

mn3

) = u(I

) + w(I

)



i=1

p(x

, x

(H12)

In turn, Eq. (H12) suggests a general recurrence formula deﬁning the interval I =

u

 corresponding to any string a

...a

of length N made from a source

X =

{

, x

,...,x

}

of size n, with the string being terminated by symbol x

The start and stop values of the corresponding interval are computed by successive

iterations from k = 2tok = N according to the following recurrence relations:











= u

k−1

+ w

k−1

Q(X, a

, a

,...,a

k−1

)

= u

k−1

+ w

k−1

R(X, a

, a

,...,a

k−1

)

= v

− u

(H13)

with











Q(X, a

, a

,...,a

k−1

) =

n−1



i=1

p(x

, a

,...,a

k−1

)

R(X, a

, a

,...,a

k−1

) =



i=1

p(x

, a

,...,a

k−1

) = 1,

(H14)

and with the initial conditions











given a

= x











0; j = 1

j−1



i=1

p(x

); j > 1

= u

+ p(x

(H15)

We note that R(X, a

, a

,...,a

k−1

) = 1, by application of the property



x∈X

p(x|y) = 1 for any event y (see Chapter 5), therefore, the sum involved in

the deﬁnition of R does not need to be computed. From this property, we also have

1 = R(X, a

, a

,...,a

k−1

) = Q(X, a

, a

,...,a

k−1

) + p(x

, a

,...,a

k−1

), which

eliminates the need to compute the sum involved in the function Q as well. We can

then redeﬁne the algorithm in Eq. (H13) according to the much simpler form:











= u

k−1

+ w

k−1

[

1 − p(x

, a

,...,a

k−1

)

]

= w

k−1

= v

− u

(H16)

Arithmetic coding algorithm 609

It is easily veriﬁed that Eqs. (H15) and (H16) yield the correct values u

for the

strings of lengths N = 1 ...3 previously analyzed. Note that the algorithm deﬁned by

these equations is valid only for the case of interest where the last symbol of the message

string, a

, is equal to x

. This algorithm represents a simpler variant of that described

in the reference

, which is valid for any symbol values of a

(namely all subintervals).

The generalization of the above algorithm to the general case (a

= x

) simply consists

of modifying Eq. (H14)to:











Q(X, a

, a

,...,a

k−1

) =

j−1



i=1

p(x

, a

,...,a

k−1

)

R(X, a

, a

,...,a

k−1

) =



i=1

p(x

, a

,...,a

k−1

(H17)

with, by convention, Q being set to zero when j = 1.

D. J. C. MacKay, A Short Course in Information Theory (1995), www.inference.phy.cam.ac.uk/mackay/info-

theory/course.html; see also D. J. C. MacKay, Information Theory, Inference and Learning Algorithms

(Cambridge, UK: Cambridge University Press, 2003), p. 113.

Appendix I (Chapter 10) Lempel–Ziv

distinct parsing

In this appendix I show, based on the demonstration of Cover and Thomas (1991)

and

a few useful explanations, that for a given string sequence (or message) of length n, the

number of distinct-parsing phrases c(n) is bounded according to:

c(n) ≤

(1 − ε

)logn

, (I1)

where ε

vanishes as n →∞.

Distinct parsing

This is the action of partitioning a given message into different substrings, or phrases,

with variable length m. Assume that the maximum phrase length allowed is K .The

number of distinct phrases having m bits is 2

. The length L

of a sequence made from

concatenating all possible phrases of length ≤K is, therefore,



m=1

. (I2)

In a note at the end of this appendix, I show that this length is equal to

= (K − 1)2

K +1

+ 2. (I3)

Consider ﬁrst the simple case where the message length is n = L

.Thenumber of

phrases c(n) in this message is maximized when the phrases are as short as possible,

meaning that there are 2

phrases of size m for each m. This yields an upper bound for

c(n), which can be developed according to:

c(n) ≤



m=1

1 − 2

K +1

1 − 2

− 2

= 2

K +1

− 2,

(I4)

T. M. Cover and J. A. Thomas, Elements of Information Theory (New York: John Wiley & Sons, 1991),

p. 320–1.

Lempel–Ziv distinct parsing 611

< 2

K +1

≤

− 2

k − 1

where K > 1 is assumed.

Consider next the more complex case where the message length satisﬁes L

≤ n <

K +1

. We can write n = L

+ 

, where 

is bounded by the difference L

K +1

−

= K 2

K +2

+ 2 −[(K − 1)2

+ 2] = (K + 1)2

,or

< (K + 1)2

. The parsing

generates a certain number of phrases of length ≤K , with the rest being of length K + 1.

The maximum number of phrases of length K + 1is2

K +1

, which is strictly greater than



/(K + 1). Thus, the upper bound for c(n) is now given by:

c(n) <

k − 1



K + 1

+ 

k − 1



K + 1

−



K − 1

+ 

k − 1



(K − 1) −

(K + 1)

− 1

+ 

k − 1

−

2

− 1

≤

+ 

k − 1

≡

k − 1

(I5)

The next step is to bound K (ﬁnd the maximum value of K ) with respect to n. Assume

most generally that L

≤ n ≤ L

K +1

. The ﬁrst inequality with Eq. (I3)gives

n ≥ L

= (K − 1)2

K +1

+ 2

≥ 2

(I6)

The lower bound 2

in Eq. (I6) is found by setting K = 1 then K > 1. There is equality

in the ﬁrst case, and in the second case we have

(K − 1)2

K +1

+ 2 > 2

K +1

+ 2 > 2

K +1

> 2

The result in Eq. (I6) implies:

K ≤ log n. (I7)

612 Appendix I

The second inequality with Eqs. (I3) and (I7) gives

n ≤ L

k+1

= K 2

K +2

+ 2

≥ K 2

K +2

+ 2.2

K +2

= (K + 2)2

K +2

≤ (log n + 2)2

K +2

(I8)

Hence,

K + 2 ≥ log

log n + 2

, (I9)

which, with the condition n > 1, develops into

K − 1 ≥ log

log n + 2

− 3

= log n − log(log n + 2) −3



1 −

log(log n + 2) + 3

log n



log n.

(I10)

If we assume n ≥ 4, we have log n + 2 ≤ 2logn and, consequently, log(log n + 2) ≤

log(2 log n) = log log n + 1. Substituting this inequality in Eq. (I10) yields

K − 1 ≥



1 −

log(log n) +4

log n



log n

≡ (1 −ε

)logn,

(I11)

with

log(log n) +4

log n

. (I12)

We now require that K − 1 > 0 (a condition which has been overlooked in the refer-

ence).

Since we already assumed n ≥ 4(logn ≥ 2), this extra requirement is equivalent

to ε

< 1. Letting n = 2

(q > 0 and real) and substituting in Eq. (I12), we obtain the new

condition log q < q − 4. As easily checked, a sufﬁcient condition is q ≥ 8orn ≥ 128

(the exact condition being n ≥ 109).

Under the condition ε

< 1(orK − 1 > 0), substituting the inequality in Eq. (I11)

into that in Eq. (H5) to obtain the ﬁnal result:

c(n) ≤

K − 1

≤

(1 − ε

)logn

(I13)

T. M. Cover and J. A. Thomas, Elements of Information Theory (New York: John Wiley & Sons, 1991),

p. 320–1.

Lempel–Ziv distinct parsing 613

Proof of Eq. (I3)

Setting q = 2, we write the sum in Eq. (I2)intheform



m=1

= q



m=1

m−1

= q



m=1

= q



m=0

Since the sum involved in the last right-hand side is equal to (1 −q

K +1

)/(1 − q), we

get

= q



1 − q

K +1

1 − q



−(K + 1)q

(1 − q) − (1 −q

K +1

)(−1)

(1 − q)

≡

q=2

q[1 −q

K +1

+ (K + 1)q

]

= q[1 −q

K +1

+ (K + 1)q

= q + q

K +1

(1 − q) + Kq

K +1

≡

q=2

2 + (K + 1)q

K +1

Appendix J (Chapter 11)

Error-correction capability of linear

block codes

In this appendix, I show that linear block codes have the capability of correcting any

error patterns of Hamming weight w(E) = e, or any number of e errors in the received

block code, provided that

e ≤



min

− 1

, (J1)

where d

min

is the minimum Hamming distance, and with the brackets corresponding to

the integer-ﬂoor deﬁnition, i.e., {(d

min

− 1)/2}≡(d

min

− 1)/2 corresponding to the

highest integer contained in the argument.

To show this, assume a block code C, with a minimum Hamming distance d

min

.To

recall, d

min

represents the minimum number of bit positions for which two codewords

differ in C.LetX be any codeword belonging to C, and Y any received block code,

which may contain errors. Deﬁne the Hamming distance between vectors X and Y as

d(X, Y ). It is clear that if d(X, Y ) < d

min

, or equivalently,

d(X, Y ) ≤ d

min

− 1, (J2)

the block code Y does not belong to C. In this case, any possible error pattern is detected

by the code.

Assume next that X and Y are the transmitted and received vectors, respectively. Since

the minimum Hamming distance d

min

is either an odd or an even integer, we can write

2t + 1 ≤ d

min

≤ 2t + 2, (J3)

where t ≥ 0 is an integer. I am now going to show that the code is capable of correcting

all error patterns having t or fewer errors.LetZ be another vector in C.Usingthe

distance property referred to as triangle inequality (see Chapter 5), we have

d(X, Z ) ≤ d(X, Y ) +d(Y, Z). (J4)

Suppose now that the number of errors in the received vector Y is w(E) = e. This means

that

d(X, Y ) = e. (J5)

The following demonstration is inspired and adapted from S. Lin and D. J. Costello, Error Control Coding

(Englewood Cliffs, NJ: Prentice-Hall, 1983).

Error-correction capability of linear block codes 615

Since both vectors X and Z belong to the code, their Hamming distance satisﬁes

d(X, Z ) ≥ d

min

, or using the left-hand side inequality in Eq. (J3):

d(X, Z ) ≥ d

min

≥ 2t + 1. (J6)

Combining Eqs. (J4), (J5), and (J6), we then obtain:

2t + 1 ≤ d

min

≤ d(X, Z )

≤ e + d(Y, Z)

⇒ d(Y, Z ) ≥ 2t + 1 −e

⇒ d(Y, Z )> 2t − e.

(J7)

To interpret the last inequality, consider the two possible cases: (a) e ≤ t, and (b) e > t.

In case (a), we obtain 2t − e > t, thus, d(Y, Z) > t. Since in this case and from

Eq. (J5)wealsohaved(Y, X ) = e ≤ t, this means that the received vector Y is closer to

the transmitted vector X than any other vector Z in the code. The principle of maximum

likelihood decoding (see Chapter 11) ensures that the code will necessarily correct the

received block Y to the transmitted block X .UsingEq.(J3), with e ≤ t,wealsohave

2e +1 ≤ 2t + 1

≤ d

min

⇒ e ≤

min

− 1

⇒ e ≤

min

− 1

(J8)

The last inequality in the above result, thus, establishes that the code is capable of

correcting all error patterns E having up to (d

min

− 1)/2 errors.

Consider next case (b), where e > t. I am going to show that the code is not capable of

correcting all the corresponding possible error patterns, because there exists at least one

case where the received vector Y is closer to an incorrect vector Z than to the transmitted

vector X . To show this, let X and Y be the transmitted and received vectors, respectively,

and assume that:

(1) Z is another vector in the code C such that d(X, Z ) = d

min

;

(2) E

and E

are two different error patterns satisfying the properties:

(i) E

+ E

= X + Z,

(ii) E

and E

do not have nonzero bits in the same positions.

Deﬁning w(U) as the Hamming weight of the block or vector U , the consequences of

the above assumptions are summarized by:







w(E

+ E

) = w(X + Z )

w(E

+ E

) = w(E

) + w(E

)

w(X + Z ) = d(X, Z) = d

min

⇔w(E

) + w(E

) = w(X + Z ) = d(X, Z ) = d

min

(J9)

616 Appendix J

The ﬁrst and second equalities in Eq. (J9) obviously stem from properties (i) and (ii),

respectively. The third equality, w(X + Z ) = d(X, Z ), comes from the deﬁnition of the

Hamming distance, which represents the number of bit positions by which two blocks or

vectors differ from each other; each of the nonzero bits in the vector X + Z represents

such positions, which number as w(X + Z).

Assume next that E

is the error vector of the transmitted vector X . The received

vector is, therefore:

Y = X + E

. (J10)

The Hamming distances d(X, Y ) and d(X, Z ) are found using results in Eq. (J10) and

property (i), respectively, as follows:

d(X, Y ) = w(X + Y ) = w(X − Y ) = w(E

), (J11)

d(Y, Z ) = w(Y + Z) = w(X + E

+ Z ) = w(X − E

+ Z ) = w(E

). (J12)

We assume next that the error pattern associated with E

corresponds to a number of

errors w(E

) = e strictly greater than t, i.e., e > t or e ≥ t + 1. Based on this assumption

and after Eqs. (J3) and (J9), we have







min

= w(E

) + w(E

) ≤ 2t + 2

t + 1 +w(E

) ≤ w(E

) + w(E

) ≤ 2t + 2

⇒ w(E

) ≤ t + 1. (J13)

Substituting w(E

) ≥ t + 1 and w(E

) ≤ t + 1 in Eqs. (J11) and (J12), we obtain

ﬁnally:



d(X, Y ) ≥ t + 1

d(Y, Z ) ≤ t + 1

⇒ d(Y, Z ) ≤ d(X, Y ). (J14)

The above result indicates that there exists an error pattern with e > t errors, which

results in a transmitted vector Y closer to an incorrect vector Z than the transmitted vector

X. As a consequence, based on the principle of maximum-likelihood decoding, the code

will output an incorrectly decoded block. This provides the proof that the code is capable

of correcting any error pattern with number of errors e ≤ t,ore ≤{(d

min

− 1)/2}, where

the brackets indicate the integer contained in the argument.