Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.

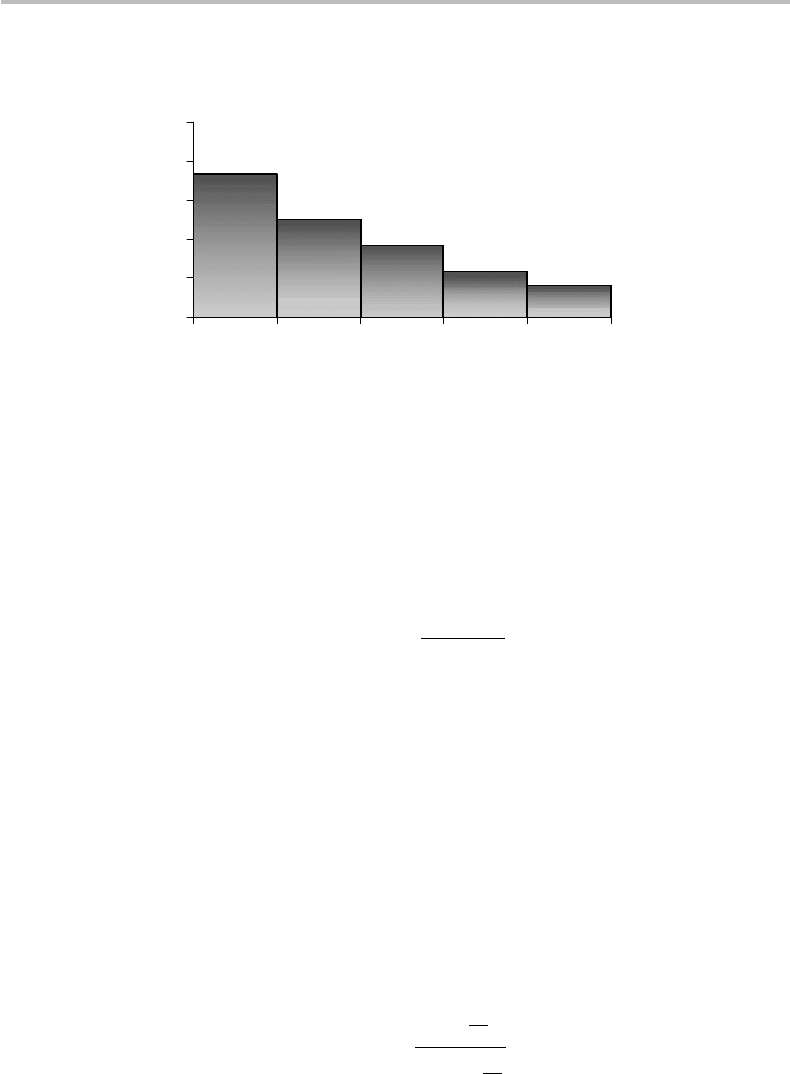
Maximum entropy of discrete sources 577
0.0
0.1
0.2
0.3
0.4
0.5
12345
0.1 3.9 7.1 11.5 15.3
i
m
)(
iii
mxpp
==
Figure C1 PDF obtained with |µ|=0.1, k = 5, and m
1
= 0.1, m
2
= 3.9, m
3
= 7.1,
m
4
= 11.5, m
5
= 15.3.
(a) m
1
, m
2
,...,m
k
are ordered positive real numbers with m
1
= 0;
(b) k is finite;
(c) µ<0 (again to ensure denominator convergence in Eq. (C19).
In this case, the PDF solution is
p
i
=
e
−m
j
|µ|
k
i=1
e
−m
j
|µ|
. (C21)
Figure C1 shows a plot of this PDF obtained, for example, with |µ|=0.1, k = 5, and
m
1
= 0.1, m
2
= 3.9, m
3
= 7.1, m
4
= 11.5, m
5
= 15.3.
In physics, this distribution characterizes the atomic populations of electrons within
a set of k energy levels, when the atoms are in a state of thermal equilibrium. To be
specific, let µ =−hν/k
B
T , with:
hν = photon energy at frequency ν (h = Planck’s constant),
k
B
T = phonon energy at absolute temperature T (k
B
= Boltzmann’s constant),
m
i
= energy of atomic level i divided by hν.
The distribution in Eq. (C21) then takes the form:
p
i
=
e
−m
j
hν
k
B
T
k
i=1
e
−m
j
hν
k
B
T
, (C22)
which is known as the Maxwell–Boltzmann distribution. This distribution shows that at
thermal equilibrium, the electron population is highest in the lowest energy level, and
decreases exponentially as the energy of the level increases. In particular, the population

578 Appendix C
ratio between two atomic levels i and j is given by
p
i
p
j
=
e
−m
j
hν
k
B
T
e
−m
j
hν
k
B
T
=
e
−(m
j
−m
j
)
hν
k
B
T
≡
e
−
E
ij
k
B
T
, (C23)
where E
ij
= (m
i
− m
j
)hν is the energy difference between the two levels. The inter-
esting conclusion of this analysis is that at thermal equilibrium electrons randomly
occupy the atomic energy levels according to a law of maximal entropy. It can be shown
that:
3
H
max
=m
hν
k
B
T
=
hν
k
B
T
exp
hν
k
B
T
− 1
.
(C24)
This results expresses in nats (1 nat = 1.44 bit) the average information contained in
an atomic system at temperature T with energy levels separated by E = hν, with
hν k
B
T . The same result holds for a two-level atomic system (k = 2). The quantity
mhν represents the mean thermal energy stored in the atomic system. The ratio
mhν/k
B
T represents the mean number of thermal phonons required to bring the atom
into this mean-energy state.
3
By definition, the source entropy is H =−
i
p
i
logp
i
. By convention, we take here the natural logarithm
so that the unity of entropy is the nat. With solution p
i
= Q
m
i
/P (and P =
i
Q
m
i
), we obtain:
H =−
i
Q
m
i
P
log
Q
m
i
P
=−
i
Q
m
i
P
(log Q
m
i
− log P)
=−
i
Q
m
i
P
m
i
log Q +
i
Q
m
i
P
log P,
which gives H =−mlog Q + log P. We now develop the second term:
log P = log
3
k
i=1
Q
m
i
4
= log(Q
m
1
+ Q
m
2
+···+Q
m
k
)
= log[Q
m
1
(1 + Q
m
2
−m
1
+···+Q
m
k
−m
1
)].
Substituting Q = exp(−
hν
k
B
T
)andE
ij
= (m
i
− m
j
)hν into the preceding, we obtain:
H =m
hν
k
B
T
+ log
exp
−m
1
hν
k
B
T
1 +exp
−
E
21
k
B
T
+···+exp
−
E
k1
k
B
T
%
.
For simplicity, we can assume that the energy levels are all equidistant, i.e. E
ij
≡ E = hν and E
k1
≡
(k − 1)hν. Using the geometric series formula 1 +q + q
2
+···+q
k−1
= (1 −q
k
/1 −q), the entropy is:
H =m
hν
k
B
T
+ log
1 −exp
−k
hν
k
B
T
1 −exp
−
hν
k
B
T
.

Maximum entropy of discrete sources 579
Discrete distributions maximizing entropy under additional constraints
In this last section, we consider a general method of deriving discrete PDFs, which
maximize entropy while being subject to an arbitrary number of constraints.
Assume, for instance, that the constraints correspond to the different PDF moments
x
0
=1, x=N, x
2
,...,x
n
, which can be expressed according to:
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
s
0
= 1 −
i
p
i
= 0
s
1
= N −
i
x
i
p
i
= 0
s
1
=x
2
−
i
x
2
i
p
i
= 0
...
s
n
=x
n
−
i
x
n
i
p
i
= 0.
(C25)
The functional f to be minimized with the Lagrange multipliers λ
0
,λ
1
,λ
2
,...,λ
n
is
then
f = H (X) + λ
0
i
p
i
+ λ
1
i
x
i
p
i
+ λ
2
i
x
2
i
p
i
+···+λ
n
i
x
n
i
p
i
. (C26)
Taking the derivative of f with respect to p
j
yields the development:
d
f
d
p
j
=
d
d
p
j
H(X ) + λ
0
i
p
i
+ λ
1
i
x
i
p
i
+ λ
2
i
x
2
i
p
i
+···+λ
n
i
x
n
i
p
i
=−
d
d
p
j
i
p
i
log p
i
+ λ
0
d
d
p
j
i
p
i
+ λ
1
d
d
p
j
i
x
i
p
i
+ λ
2
d
d
p
j
i
x
2
i
p
i
+···+λ
n
d
d
p
j
i
x
n
i
p
i
=−log p
j
− 1 + λ
0
+ λ
1
x
j
+ λ
2
x
2
j
+···+λ
n
x
n
j
= 0, (C27)
Considering a two-level atomic system (k = 2), we have, in particular;
H =m
hν
k
B
T
+ log
⎡
⎢
⎢
⎣
1 − exp
−2
hν
k
B
T
1 − exp
−
hν
k
B
T
⎤
⎥
⎥
⎦
=m
hν
k
B
T
+ log
1 + exp
−
hν
k
B
T
.
If we assume as well that hν/(k
B
T ) is large enough that the exponential can be neglected, we obtain
H ≈m
hν
k
B
T
, which is valid for all systems with k ≥ 2. It is then straightforward to determine m, from
the definition m=m
1
p
1
+ m
2
p
2
. The result is the well known “mean occupation number” of Boltzmann’s
distribution:
m=
1
exp
hν
k
B
T
− 1
.

580 Appendix C
which corresponds to the general PDF solution
p
j
= exp
λ
0
− 1 + λ
1
x
j
+ λ
2
x
2
j
+···+λ
n
x
n
j
, (C28)
or
p
j
= A
0
A
x
j
1
A
x
2
j
2
...A
x
n
j
n
(C29)
with
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎩
A
0
= exp(λ
0
− 1)
A
1
= exp(λ
1
)
A
1
= exp(λ
2
)
...
A
n
= exp(λ
n
).
(C30)
The solutions in Eq. (C29) and (C30) for λ
0
,λ
1
,λ
2
,...,λ
n
using the n + 1 constraints
in Eq. (C25) can only be found numerically. An example of a resolution method and
its PDF solution in the case n = 2, the event space X being the set of integer numbers,
can be found in.
4
In these references, it is shown that the photon statistics of optically
amplified coherent light (i.e., laser light passed through an optical amplifier) is very
close to the PDF solution of maximal entropy.
It is straightforward to show that in the general case, the maximum entropy is given
by the following analytical formula:
5
H
max
= 1 − (λ
0
+ λ
1
x+λ
2
x
2
+···+λ
n
x
n
)
= 1 −
n
i=0
λ
i
x
i
.
(C31)
Further discussion and extensions of the continuous PDF case of the entropy-
maximization problem can be found in.
6
4
E. Desurvire, How close to maximum entropy is amplified coherent light? Opt. Fiber Technol., 6 (2000),
357. E. Desurvire, Erbium-Doped Fiber Amplifiers, Device and System Developments (New York: John
Wiley & Sons, 2002), Ch. 3, p. 202.
5
We have
H =−
j
p
j
log p
j
=−
p
j
log
A
0
A
x
j
1
A
x
2
j
2
...A
x
n
j
n
=−
p
j
log A
0
+ x
j
log A
1
+ x
2
j
log A
2
+···+x
n
j
log A
n
.
=−
log A
0
p
j
+ log A
1
x
j
p
j
+ log A
2
x
2
j
p
j
+···+log A
n
x
n
j
p
j
=−(λ
0
− 1 + λ
1
x +λ
2
x
2
+···+λ
n
x
n
)
6
T. M. Cover and J. A. Thomas, Elements of Information Theory (New York: John Wiley & Sons, 1991),
Ch. 11, p. 266.

Appendix D (Chapter 5) Markov chains
and the second law of
thermodynamics
In this appendix, I shall first introduce the concept of Markov chains, then use it with
the results of Chapter 5 concerning relative entropy (or Kullback–Leibler distance) to
describe the second law of thermodynamics.
Markov chains and their properties
Consider a source X of N random events x with probability p(x). If we look at a
succession of these events over time, we then observe a series of individual outcomes,
which can be labeled x
i
(i = 1 ...n), with x
i
∈ X
n
. The resulting series, which is, thus,
denoted x
1
...x
n
, forms what is called a stochastic process.
Such a process can be characterized by the joint probability distribution
p(x
1
, x
2
,...,x
n
). In this definition, the first argument x
1
represents the outcome
observed at time t = t
1
, the second represents the outcome observed at time t = t
2
,
and so on, until observation time t = t
n
. Then p(x
1
, x
2
,...,x
n
) is the probability of
observing x
1
, then x
2
, etc., until x
n
. If we repeat the observation of the n events, but
now starting from any time t
q
(q > 1), we shall obtain the series labeled x
1+q
...x
n+q
,
which corresponds to the joint distribution p(x
1+q
, x
2+q
,...,x
n+q
). By definition, the
stochastic process is said to be stationary if for any q we have
p(x
1+q
, x
2+q
,...,x
n+q
) = p(x
1
, x
2
,...,x
n
), (D1)
meaning that the joint distribution is invariant with time translation. Note that such an
invariance does not mean that x
1+q
= x
1
, x
2+q
= x
2
, and so on! The property only means
that the joint probability is time invariant, or does not depend at what time we start the
observation and which time intervals we use between two observations.
What is a Markov process? Simply defined, it is a chain process where the event
outcome at time t
n+1
is only a function of the outcome at time t
n
, and not of any other
preceding events. Such a property can be written formally as:
p(x
n+1
|x
n
, x
n−1
,...,x
1
) ≡ p(x
n+1
|x
n
). (D2)
This means that the event x
n+1
is statistically independent, in the strictest sense,
from all preceding events but x
n
. Using Bayes’s formula and the above property,

582 Appendix D
we get:
p(x
1
, x
2
) = p(x
2
|x
1
)p(x
1
)
p(x
1
, x
2
, x
3
) = p(x
3
|x
1
, x
2
)p(x
1
, x
2
) = p(x
3
|x
2
)p(x
2
|x
1
)p(x
1
)
etc.,
(D3)
and consequently
p(x
1
, x
2
,...,x
n
) = p(x
n
|x
n−1
)p(x
n−1
|x
n−2
) ... p(x
2
|x
1
)p(x
1
). (D4)
A Markov chain is said to be time invariant if the conditional probabilities p(x
n
|x
n−1
)do
not depend on the time index n, i.e., they are themselves time invariant. For instance, if a
and b are two specific outcomes, we have p(x
n
= b|x
n−1
= a) = p(x
n−1
= b|x
n−2
= a)
=···=p(x
2
= b|x
1
= a). If we recall the property of conditional probabilities:
p(y) =
x∈X
p(y|x) p(x), (D5)
then we have for time-invariant Markov chains (as applying to any time t
n+1
):
p(x
n+1
) =
x
n
∈X
p(x
n+1
|x
n
)p(x
n
), (D6)
or equivalently
p(x
n+1
) =
x
n
∈X
p(x
n
)P
x
n
x
n+1
, (D7)
where we define P
x
n
x
n+1
≡ p(x
n+1
|x
n
) as being the coefficients of a certain transition
matrix P (note the reverse order of the coefficient subscripts). Such a transition matrix
uniquely defines the Markov chain, and defines the evolution of any other probability
distribution q, namely:
q(x
n+1
) =
x
n
∈X
q(x
n
)P
x
n
x
n+1
. (D8)
The expressions in Eqs. (D7)or(D8) correspond to a matrix-vector equation. The matrix
P is, thus, applied to transform the N -vector of coordinates p(x = x
n
), x ∈ X, which we
call µ. The result of such a transformation is an N -vector of coordinates p(x = x
n+1
),
x ∈ X, which we call µ
. The matrix-vector equation (Eq. (D7)) is, thus, summarized in
the form:
µ
= µP. (D9)
To take a practical example, consider the 2 × 2 transition matrix that corresponds to a
two-state Markov chain (X being made of two events):
P =
P
11
P
12
P
21
P
22
=
α 1 −α
β 1 − β
, (D10)

Markov chains and the second law of thermodynamics 583
where α, β are real constants. This means that this Markov process is time invariant.
Replacing this definition in Eq. (D10), we obtain:
µ
≡ (µ
1
,µ
2
)
= µP
= (µ
1
,µ
2
)
α 1 − α
β 1 −β
≡ [αµ
1
+ βµ
2
, (1 − α)µ
1
+ (1 −β)µ
2
].
(D11)
Since the input coordinates satisfy µ
1
+ µ
2
= 1 (being probabilities), we observe that
the sum of the output coordinates is also unity, µ
1
+ µ
2
= µ
1
+ µ
2
= 1, which justifies
our choice for the time-invariant transition matrix P (it is easily shown that this is
actually the only one).
This example will help us to illustrate yet another important concept. We have seen
that a Markov process can be time invariant, meaning that the transition matrix has
constant or unchanging coefficients. But this time invariance does not mean that the
probability distribution does not change over time: we have just seen from our previous
example that in the general case µ
= µ, which means that p(x) at time t
n+1
is generally
different from p(x) at time t
n
. But nothing forbids the distribution from remaining
unchanged over time. By definition, we shall say that the distribution µ is stationary if
the following property is satisfied:
µ
= µP = µ. (D12)
With the previous example, it is easily established that the stationary solution satisfies:
µ
1
= p(x
1
) =
β
1 − α + β
µ
2
= p(x
2
) =
1 − α
1 − α + β
,
(D13)
with the condition α − β = 1. Such a distribution is of the type p(x
1
) = β/M and
p(x
2
) = 1 − β/M, where M = 1 −α + β, meaning that it is generally nonuniform.
The specific case of a uniform stationary distribution is given by β = M/2, which gives
p(x
1
) = p(x
2
) = 1/2.
The lesson learnt from the above example is that time-invariant Markov processes
have stationary solutions. If the process is initiated at time t
1
with a stationary solution,
then the process is also stationary, meaning that the probability distribution p(x) at time
t
n+1
is the same as at time t
n
or t
n−1
or t
1
. Note that such a stationary solution is not
necessarily unique. Two conditions for uniqueness of the stationary solution,
1
which we
will assume here without demonstration, are:
(a) The process is aperiodic (i.e., the evolution of p(x) does not show periodic oscilla-
tions with equal or increasing amplitudes);
(b) There exists a nonzero probability that the variable x ∈ X will be reached within a
finite number of steps (the process is then said to be irreducible).
1
T. M. Cover and J. A. Thomas, Elements of Information Theory (New York: John Wiley & Sons, 1991),
Ch. 2.

584 Appendix D
Under these two conditions, the stationary solution is unique. Moreover, the distri-
bution at time t
n
in the limit n →∞asymptotically converges towards the stationary
solution, regardless of the initial distribution at time t
1
. This property will be demon-
strated in the second part of this appendix.
Assuming that the conditions of uniqueness are satisfied in the previous example, the
entropy H(X )
t=t
n
converges towards the limit:
H(X )
t=t
∞
≡ H
∞
=−µ
1
log µ
1
− µ
2
log µ
2
=−
β
M
log
β
M
−
1 −
β
M
log
1 −
β
M
.
(D14)
It is easily verified that when the stationary solution is uniform (β = M/2), then
H
∞
= H
max
= log 2 ≡ 1 bit/symbol, which represents the maximum possible entropy
for a two-state distribution (Chapter 4). In the general case where the stationary solution
is nonuniform (β = M/2), we have, therefore, H
∞
< H
max
. This means that the system
evolves towards an entropy limit that is lower than the maximum. Here comes the inter-
esting conclusion for this first part of the appendix: assuming that the initial distribution
is uniform and the stationary solution nonuniform, the entropy will converge to a value
H
∞
< H
max
= H (X)
t=t
1
. This result means that the entropy of the system decreases
over time, in apparent contradiction with the second law of thermodynamics. Such a
contradiction is lifted by the argument that a real physical system has no reason to be
initiated with a uniform distribution, giving maximum entropy for initial conditions. In
this case, and if the stationary distribution is uniform, then the entropy will grow over
time, which represents a simplified version of the second law, as we shall see in the
second part. Note that the stationary distribution does not need to be uniform for the
entropy to increase. The condition H
∞
> H (X)
t=t
1
is sufficient, and it is in the domain
of physics, not mathematics, to prove that such a condition is representative of real
physical systems.
Proving the second law of thermodynamics
The second part of this appendix provides an elegant information-theory proof of the
second law of thermodynamics.
2
The tool used to establish this proof is the concept
of relative entropy, also called the Kullback–Leibler distance, which was introduced in
Chapter 5.
Considering two joint probability distributions p(x, y), q(x, y), the relative entropy
is defined as the quantity:
D[ p(x, y)q(x, y)] =
log
p(x, y)
q(x, y)
!
X,Y
=
x∈X
y∈Y
p(x, y)log
p(x, y)
q(x, y)
.
(D15)
2
T. M. Cover and J. A. Thomas, Elements of Information Theory (New York: John Wiley & Sons, 1991),
Ch. 2.

Markov chains and the second law of thermodynamics 585
In particular, it was shown that the relative entropy obeys the chain rule:
D[ p(x, y)q(x, y)] = D[p(x)q(x)] + D[ p(y|x)q(y|x)]
= D[ p(y)q(y)] + D[ p(x|y)q(x|y)],
(D16)
where D[p(.|.)q(.|.)] is a conditional relative entropy. Finally, an important property
is that the relative entropy is always positive (regardless of the arguments being joint
or conditional probabilities), except in the specific case p = q, where it is zero (thus,
D[ pq] > 0if p = q and D[ pp] = D[qq] = 0).
We shall apply the above properties to the case of Markov chains. In this analysis, the
variables x
n
and x
n+1
are substituted for the variables x and y, which define the system
events from a single source X that can be observed at two successive instants (x
n
, x
n+1
∈ X ). Let us assume now that the system evolution is characterized by a time-invariant
Markov process. Such a process is defined by a unique transition probability matrix R,
which has the time-independent elements R
x
n
x
n+1
= r(x
n+1
|x
n
). Consistently with the
property in Eq. (D2), the conditional probabilities are uniquely defined for p and q:
p(x
n+1
|x
n
) ≡ r(x
n+1
|x
n
)
q(x
n+1
|x
n
) ≡ r(x
n+1
|x
n
),
(D17)
Next, we apply the chain rule in Eq. (D16):
D[ p(x
n+1
, x
x
)q(x
n+1
, x
x
)] = D[ p(x
x
)q(x
x
)] + D[ p(x
n+1
|x
n
)q(x
n+1
|x
n
)]
= D[ p(x
x+1
)q(x
x+1
)] + D[ p(x
n
|x
n+1
)q(x
n
|x
n+1
)].
(D18)
Substituting Eq. (D17)inEq.(D18), we obtain
D[ p(x
x
)q(x
x
)] + D[r(x
n+1
|x
n
)r(x
n+1
|x
n
)]
= D[ p(x
x+1
)q(x
x+1
)] + D[ p(x
n
|x
n+1
)q(x
n
|x
n+1
)],
(D19)
or equivalently, since D[rr] = 0:
D[ p(x
x+1
)q(x
x+1
)] = D[ p(x
x
)q(x
x
)] − D[ p(x
n
|x
n+1
)q(x
n
|x
n+1
). (D20)
Considering the property D[pq] ≥ 0, Eq. (D20) shows that D[ p(x
x+1
)q(x
x+1
)] ≤
D[ p(x
x
)q(x
x
)]. This result means that in a time-invariant Markov process, the relative
entropy or distance between any two distributions can only decrease over time.
In particular, we can choose q = q
st
to be a stationary solution of the Markov process.
If this solution is unique, then its distance for any other distribution p decreases over
time. This means that p converges to the asymptotic limit defined by q
st
(it can be shown,
although it is not straightforward, that D[pq
st
] = 0or p ≈ q
st
in this limit).
Assume next that the stationary solution of the Markov process is a uniform distri-
bution, which we shall call u
st
(namely, u
st
(x) = 1/N , x ∈ X). From the definition of

586 Appendix D
distance (Eq. (D15) applied to single-variable distributions), we obtain
D[ pu
st
)] =
x∈X
p log
p
1/N
=
x∈X
p log p +
x∈X
p log N
≡ H
max
− H (X),
(D21)
with H
max
= log N. Since the distance decreases over time while staying positive, the
above result means that the system entropy H(X ) increases over time towards the upper
limit H
max
.
This demonstration could be considered to represent one of several possible proofs of
the second law of thermodynamics. We should not conclude that the second law implies
that the stationary solution of any physical system must be uniform! What was shown is
simply that this condition is sufficient, short of being necessary.
