Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.

25.8 Electromagnetic waves, polarization states, photons, and quantum measurements 547
hereafter). Occasionally, I shall designate the right- and left-circular polarization states
by the symbols ∪ and ∩, respectively.
Back to complex notation, we may represent the circularly polarized E-fields according
to the decomposition:
E =
1
|
E
|
e
i
δϕ
2
e
−i
δϕ
2
e
iωt
=
e
i
δϕ
2
|
E
|
1
0
e
iωt
+
e
−i
δϕ
2
|
E
|
0
1
e
iωt
= e
iϕ
1
|
E
|
1
0
e
iωt
+
e
−iδϕ
|
E
|
0
1
e
iωt
,
(25.13)
where ϕ = δϕ/2 is an arbitrary phase factor. For circularly polarized E-fields we have
E
±
= e
iϕ
1
|
E
|
1
0
e
iωt
+
e
±i
π
2
|
E
|
0
1
e
iωt
≡ e
iϕ
1
|
E
|
1
0
e
iωt
± i
1
|
E
|
0
1
e
iωt
.
(25.14)
The decomposition in Eq. (25.13) is immediately reminiscent of a quantum state super-
position! Indeed, if we define the second term in the decomposition as ±
|
1
, the super-
position is equal to
|
0
+
|
1
≡
√
2
|
+
in the upper case (+, or cw, or left-circular
polarization, or ∩), and to
|
0
−
|
1
≡
√
2
|
−
in the lower case (−, or ccw, or right-
circular polarization, or ∪). Within a normalization factor of 1/
√
2,weseethatthetwo
circularly polarized states ∩, ∪ are equivalent to the quantum states or qubits |+,
|
−
.
We can now check the states orthogonality by effecting the (Hilbert-space) scalar
product:
E
+
·
E
−
∗
=
e
iϕ
|
E
|
1
0
+ i
0
1
e
iωt
·
e
iϕ
|
E
|
1
0
− i
0
1
e
iωt
∗
=
1
|
E
|
2
1
i
·
1
i
=
1
|
E
|
2
1 + i
2
≡ 0,
(25.15)
which is the expected result, just as |+,
|
−
are orthogonal states. It is left as an easy
exercise to show that the superposition of two circularly polarized E-fields having oppo-
site directions (i.e., E
+
± E
−
) yield linearly polarized E-fields. This result is expected,
since within a 1/
√
2 normalization factor, we know for a fact that
|
+
+
|
−
=
|
0
and
|
+
−
|
−
=
|
1
. Thus, circular polarization states can be viewed as the superposition
of two linear polarization states (oscillating in quadrature), and the reverse.
The above demonstration, albeit somewhat tedious, was very well worth it: it made
it possible to reach a major conclusion: there exist four special states of polarization
for the classical E-field, which form two orthogonal bases, namely
{
, ↔
}
and
{
∩, ∪
}
,
respectively. Furthermore, there exists a one-to-one correspondence between these two

548 Classical and quantum cr yptography
bases and the quantum bases
{
|0,
|
1
}
and
{
|+,
|
−
}
, respectively. We must notice
that in order to reach this conclusion we did not need to make any assumption about
the quantum nature of light. Such an assumption will come into the picture later, when
considering single-photon measurements. It will turn out, however, that the EM field
associated with the photon is essentially described by the same
{
, ↔
}
,
{
∩, ∪
}
bases
and, therefore, the above conclusion remains fully valid at quantum scales.
Next, I shall introduce an optical component referred to as a quarter-wave plate
(QWP). As the name suggests, it is a piece of flat material, and it is transparent to
light. The material, however, is a special type of crystal exhibiting the property of
birefringence. A material is said to be birefringent if the speed of light varies according
to the polarization orientation of the incident light ray (assumed linearly polarized). Thus,
the speed of light is faster in some polarization direction (referred to as the fast axis)
and slower in the orthogonal direction (referred to as the slow axis). If the incident light
ray is parallel to either the fast or slow axes, the light polarization remains unchanged.
However, if the fast (or slow) axis forms a 45
◦
angle with the incident polarization,
the E-field component that projects onto the fast axis propagates faster than the E-field
component that projects onto the slow axis, thus, introducing a phase delay ϕ between
the two components and, hence, making the state of polarization of the ray evolve as it
traverses the plate. The additional feature of the QWP is that its thickness is precisely
calculated in order for this net phase delay to be ϕ = π/2 (corresponding to a quarter
wavelength, hence, the name). Intuitively, we may already infer that the QWP transforms
the input polarizations from linear to circular and the converse, and this inference is
absolutely correct! Let us prove such a property now. Assuming a linearly polarized
incident E-field, as defined in Eq. (25.8), and the QWP axes oriented at 45
◦
(cw) from
the vertical axis, the incident E-field is projected along the QWP fast and slow axes
according to the definition:
E
in
= e
iφ
1
√
2
E
1
+ E
2
E
1
− E
2
e
iωt
. (25.16)
After traversing the QWP, the output E-field has become
E
out
= e
iφ
1
√
2
E
1
+ E
2
e
iϕ
(
E
1
− E
2
)
e
iωt
≡ e
iφ
1
√
2
E
1
+ E
2
i
(
E
1
− E
2
)
e
iωt
.
(25.17)
Substituting E
1
= 1, E
2
= 0 (incident ray in the orientation, or aligned with the fast
axis, or, conventionally,
|
0
), we obtain:
E
out
= e
iφ
1
√
2
1
i
e
iωt
= e
iφ
1
√
2
1
0
+ i
0
1
e
iωt
,
(25.18)
which is immediately identified as the left-circular polarization state, or ∩,or
|
+
. Clearly,
the case E
1
= 0, E
2
= 1, corresponding to an incident ray in the ↔ orientation (or
25.8 Electromagnetic waves, polarization states, photons, and quantum measurements 549
aligned with the slow axis, or, conventionally,
|
1
), yields the right-circular polarization
state, or ∪,or
|
−
. Thus, the QWP converts linear polarization states into circular
polarization states, according to the transformations
|
0
→
|
+
and
|
1
→
|
−
.
Let us show next the converse operation. Assume an incident ray that is circularly
polarized, according to the base ∩or ∪(equivalently,
|
+
or
|
−
). It suffices it to substitute
E
1
= 1 and E
2
=±i in Eqs. (25.16) and (25.17) to obtain for the output E-field:
E
out
= e
iφ
1
√
2
1 ± i
i
(
1 ∓ i
)
e
iωt
= e
iφ
1
√
2
1 ± i
i ± 1
e
iωt
=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
e
iφ
1
√
2
1 + i
1 + i
e
iωt
≡ e
iφ+
π
4
1
1
e
iωt
e
iφ
1
√
2
1 − i
−
(
1 − i
)
e
iωt
≡ e
iφ−
π
4
1
−1
e
iωt
.
(25.19)
As expressed in the vertical or horizontal basis (i.e., after rotating the reference axes by
45
◦
ccw), the output E-field is, finally,
E
out
≡
⎧
⎪
⎪
⎨
⎪
⎪
⎩
e
iφ+
π
4
1
0
e
iωt
e
iφ−
π
4
0
1
e
iωt
,
(25.20)
which (within arbitrary phase factors) corresponds to the linearly polarized states (top)
and ↔ (bottom), respectively. Thus, the QWP converts circular polarization states into
linear polarization states, according to the transformations
|
+
→
|
0
and
|
−
→
|
1
,
as previously announced.
We may summarize all of the above conclusions by recalling from Chapter 16 that the
Hadamard matrix, H, precisely achieves the four transformations
⎧
⎪
⎪
⎨
⎪
⎪
⎩
H
|
0
=
|
+
H
|
1
=
|
−
H
|
+
=
|
0
H
|
−
=|1.
(25.21)
This observation establishes that a QWP device transforms the polarized EM states
(, ↔, ∩, ∪) in a way strictly equivalent to that of the Hadamard matrix, H,onthe
quantum states (|0,
|
1
|+,
|
−
).
From the above description, we have seen that it is possible to manipulate the polar-
ization states of the EM field. To progress further, we must, at this stage, take into
account the quantum nature of light, namely the particle-like behavior of the photon.
Such behavior can be readily understood by considering the two experiments illustrated
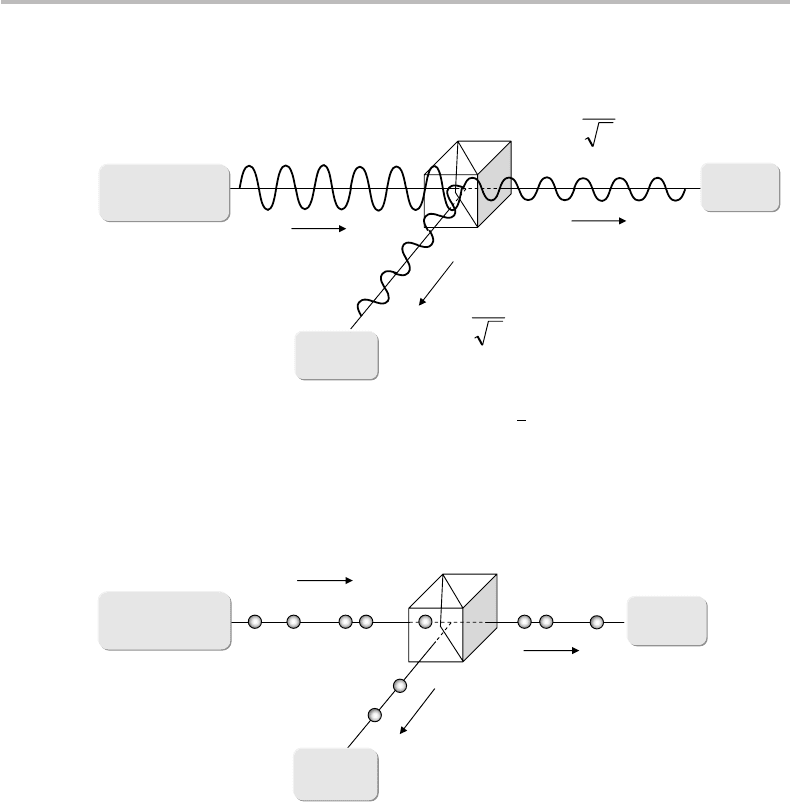
in Figs. 25.3 and 25.4. In the first experiment (Fig. 25.3), we divide an incident EM
light beam with E-field E into two beams of equal E-field amplitudes; this is achieved
through a 50:50 beamsplitter. Since the incident EM power is given by P =
|
E
|
2
,the
E-field amplitudes of the two output beams are E/
√
2. Two detectors placed on the
550 Classical and quantum cr yptography
D
2
D
1
50 : 50
Beamsplitter
Light source
E
2
E
2
E
Detector
Detector
Figure 25.3 Dividing an EM light beam (electrical field E,powerP =
|
E
|
2
) through a 50:50
beamsplitter, resulting in two beams (electrical fields E/
√
2) of detected powers both equal to
P
= P/2.
SPD
2
SPD
1
50 : 50
Beamsplitter
SP source
Detector
Detector
Figure 25.4 Same experimental apparatus as Fig. 25.3 with single photons (SP) being emitted
and detected.
output beam paths measure equal EM powers of P
= P/2, as expected. The picture
becomes very different if we reduce the EM power to the point of reaching the level of
photon granularity, i.e., the number of photons emitted per second by the light source is
of the order of unity. The experimental apparatus shown in Fig. 25.4 is basically identical
to the previous one, except that now the light source produces single photons
17
(SP) and
that the two detectors are capable of detecting such single photons. Since photons are
particle-like energy quanta, they cannot be split. On reaching the 50:50 beamsplitter,
therefore, they “choose” at random to follow one of the two possible beam paths.
18
17
The sequence of single photons emitted by a light source can be visualized as individual drops falling in a
sink from a leaking tap, or individual cars passing on a highway lane: one at time, but at random times.
18
The choice for photons to take one path or the other is dictated by the random fluctuations of the “vacuum
field,” which enters through the four th or unused port of the 50:50 beamsplitter.

25.8 Electromagnetic waves, polarization states, photons, and quantum measurements 551
The two choices have exact and equal probabilities of P = 0.5. As seen from the
figure, the key difference from the previous experiment is that the photon stream is
randomly partitioned. Each single-photon detector (SPD) receives one photon at a time,
which generates a “ping” count. A ping from detector SPD
1
means that the photon
has chosen the straight-through path, while a ping from detector SPD
2
means that
it has chosen the reflection path, as shown. If the straight-through and the reflection
paths have strictly equal lengths, there is no possibility of the detectors SPD
1
, SPD
2
generating two pings or counts simultaneously. The two-count histogram is the same
as in a coin-flipping experiment (see, for instance, Fig. 1.3). Over a sufficient period
of time, the numbers of counts from SPD
1
and SPD
2
become about equal. This is
equivalent to saying that with a sufficiently large number of photons, the light beam
has been divided into two beams of equal power, as in the previous experiment with
classical light. The second experiment, which is routinely done in the laboratory, rep-
resents one of the many physical proofs of the quantum nature of light and its photon
granularity.
From this point on, we shall assume that we are dealing with single photons, and
that the associated E-fields are in any of the four polarization states
{
, ↔
}
,
{
∩, ∪
}
or
equivalently
{
|0,
|
1
}
,
{
|+,
|
−
}
, respectively. For short, we may say that the photon “is”
in any of these quantum states. Next, I introduce two other components: the half-wave
plate (HWP) and the polarization beamsplitter (PBS).
As its name indicates, the HWP is similar to the previously described QWP, except
that the net phase delay experienced by two orthogonal E-field components is now π
or one half of a wavelength. As in the QWP case, the fast axis of the plate must be
oriented at 45
◦
of the incident E-field polarization direction, assumed linear. Since the
phase shift corresponds to a factor e
iπ
=−1, the sign of one of the two polarization
components is reversed, and the result is a 90
◦
rotation of the incident linear polarization.
Thus, the HWP swaps the basis states
{
, ↔
}
into each other, which is equivalent to
the transformations
|
0
→
|
1
and
|
1
→
|
0
, corresponding to the action of the Pauli
matrix X on the states |0,
|
1
(see Chapter 16). If the incident E-field polarization is
circular, the HWP axis orientation is unchanged, but the direction of rotation is reversed.
Thus, the effect of the HWP is to swap the basis states
{
∩, ∪
}
into each other, which
is equivalent to the transformations
|
+
→
|
−
and
|
−
→
|
+
, corresponding to the
action of the Pauli matrix Z on the states |+,
|
−
(see Chapter 16). Thus, placing a
HWP next to a linearly polarized SP source and orienting it at either 0
◦
or 45
◦
makes
it possible to generate single photons into either the
|
0
or the
|
1
linear-polarization
state. The PBS is a special assembly of birefringent crystal prisms whose effect, as the
name indicates, is to separate an incident light beam into two orthogonally polarized
components. As shown in Fig. 25.5, a detector SPD
1
placed in the s traight-through path
only detects vertically polarized, or
|
0
photons, while a detector SPD
2
placed in the
“reflection” path only detects horizontally polarized, or
|
1
photons. The PBS–SPD
1
–
SPD
2
set-up, thus, constitutes a quantum measurement apparatus to determine the state
of linearly polarized photons. If a count is obtained from SPD
1
or from SPD
2
,wemay
attribute the values +1 or –1, respectively, to these two possible measurements. Recall
from Chapter 16 that |0,
|
1
, and ±1 are the eigenvectors and eigenvalues of the Pauli

552 Classical and quantum cr yptography
SPD
2
SPD
1
0
0
1
1
PBS
Figure 25.5 Splitting a light beam of single, linearly polarized photons through a polarization
beamsplitter (PBS). The apparatus corresponds to a measurement of photon states in the Z basis.
SPD
2
SPD
1
PBS
0
+
−
1
QWP
Figure 25.6 Splitting a light beam of single, circularly polarized photons through a polarization
beamsplitter (PBS) preceded by a quarter-wave plate (QWP). The apparatus corresponds to a
measurement of photon states in the X basis.
matrix Z , according to:
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
Z
|
0
=
|
0
↔
10
0 −1
1
0
=
1
0
Z
|
1
=−
|
1
↔
10
0 −1
0
1
=−
0
1
.
(25.22)
Thus, measuring linearly polarized photons is equivalent to “observing” Z, or equiv-
alently, to operating in the measurement basis
{
|0,
|
1
}
, or, for short, in the Z
basis.
A different set-up, which involves circularly polarized photons, is shown in Fig.
25.6. The generation of left- or right-circularly polarized photons is achieved by plac-
ing a QWP (quarter-wave plate) next to a linearly polarized SP source, with its fast
axis at 45
◦
cw or ccw, respectively. A way to tell whether a photon is left- or right-
circularly polarized is to convert its polarization into a linear polarization, followed by the

25.8 Electromagnetic waves, polarization states, photons, and quantum measurements 553
Table 25.7 Probabilities p(±1) of measuring eigenvalues ±1 (counts in detectors SPD
1
or SPD
2
)
according to input photon state (, ↔, ∩, ∪or |0, |1, |+, |−) and measurement apparatus (X , Z).
Input photon state or
|
0
↔ or
|
1
∩ or
|
+
∪ or
|
−
Measurement basis XZXZXZXZ
p(+1) 0.5 1 0.5 010.5 0 0.5
p(−1) 0.5 0 0.5 100.5 1 0.5
PBS–SPD
1
–SPD
2
apparatus, as illustrated in the figure. The QWP–PBS–SPD
1
–SPD
2
set-up, thus, constitutes a quantum measurement apparatus to determine the state of
circularly polarized photons. If a count is obtained from SPD
1
or from SPD
2
,wemay
attribute the values +1 or –1, respectively, to these two possible measurements. Recall
from Chapter 16 that |+,
|
−
, and ±1 are the eigenvectors and eigenvalues of the Pauli
matrix X , according to:
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
X
|
+
=
|
+
↔
01
10
1
√
2
1
1
=
1
√
2
1
1
X
|
−
=−
|
−
↔
01
10
1
√
2
1
−1
=−
1
√
2
1
−1
.
(25.23)
Thus, measuring circularly polarized photons is equivalent to “observing” X , or equiv-
alently, to operate in the measurement basis
{
|+,
|
−
}
, or, for short, in the X basis.
Assume, next, that we have no knowledge of the input photon states. For the mea-
surement, we have the possibility of using either the X or the Z bases. What happens
if we choose t he wrong one (namely X for linearly polarized photons, and Z for cir-
cularly polarized photons)? There are two ways t o answer such a question. The first
one is a classical answer. It has been established for a fact that circular polarization is
the superposition of two orthogonal linear polarizations (oscillating in quadrature), and
the reverse. Thus, a circularly polarized E-field incident on a PBS is decomposed into
its two linear-polarization components. Likewise, a linearly polarized E-field incident
on a QWP–PBS apparatus is first transformed by the QWP into a circularly polarized
E-field, and then decomposed by the PBS into its two linear components. But this expla-
nation is valid only for classical E-fields! Indeed, consider now the case of polarized
single photons. A circularly polarized photon incident onto a PBS cannot be physi-
cally split into two linearly polarized photons. Since the photon is associated with two
linear-polarization states (oscillating in quadrature) it has to “choose” one or the other,
and such a choice comes with a 50% probability, as in the photon-beam partitioning
experiment described earlier. The same conclusion applies to the case of linearly polar-
ized photons incident on a QWP–PBS apparatus. The key conclusion is that measuring
photons with the wrong basis, i.e., circularly polarized photons with basis Z or linearly
polarized photons with basis X, produces equiprobable, random outcomes. The different
measurement possibilities are summarized in Table 25.7.

554 Classical and quantum cr yptography
We now have all the necessary tools to describe the principle of quantum cryptogra-
phy, or, more precisely, the QKD protocols. Before proceeding to a formal description
of such protocols, it is useful to consider a communication link between Alice and
Bob, and how they may be able to communicate “secret” information by means of X -
and Z -basis photon-state preparations and measurements; this is described in the next
section.
25.9 A secure photon communication channel
In this section, we assume that Alice and Bob can send light signals to each other
by means of free-space-optics or an optical fiber link, which we refer to as a photon
communication channel. Both have single-photon sources that are capable of producing
photons in any polarization states (, ↔, ∩, ∪ or |0, |1, |+, |−), and independent
photon-measurement apparatus in the X and Z bases. What is possible for Alice is the
same as for Bob, so here we only need to consider the case of Alice transmitting photons
to Bob.
As a starting point, Alice generates a random 16-bit sequence from her end, say, for
instance:
1010 0011 1110 0100.
Then Alice prepares a sequence of 16 photons, which she randomly polarizes according
to the following selection rule (for instance):
For the 1 bit, use either or ∩ polarizations at random;
For the 0 bit, use either ↔ or ∪ polarizations at random.
Consistently with the above bit sequence and random-selection rule, Alice’s preparation
yields (for instance) the following polarized-photon sequence:
↔∩∪↔↔∩∪∩↔∪∪∩.
Alice then inputs the above photon sequence through the link. At the other end, Bob
receives the photon sequence and makes 16 corresponding measurements, according
to his own random choice of X and Z basis. Table 25.8 shows Bob’s basis choices
and the outcome of each of Bob’s measurements. Conventionally, and unless otherwise
specified, a +1 eigenvalue measurement will be now called a 1 bit of information,
and a −1 measurement will be called a 0 bit of information, respectively.Thetable
shows that Bob’s random choices of X and Z measurement bases are either “right” or
“wrong.” The right basis choices correspond to measuring , ↔ with Z, and ∩, ∪ with
X. Comparing the top and bottom lines of the table, we notice that the right choices give
Bob information bits that are always correct with respect to Alice’ initial sequence. In
the other case of wrong basis choice, Bob’s information bits are inherently random and,
therefore, not correlated with those of Alice’s sequence.

25.9 A secure photon communication channel 555
Table 25.8 Alice’s 16-bit and corresponding photon-state sequence, Bob’s choice of
X
and
Z
measurement basis, and
the outcome of the measurements in terms of eigenvalues and corresponding 1 or 0 informa t ion bits. The outcomes
shown in bold correspond to Bob’s accidentally correct choices of measurement basis.
Alice’s bit sequence 1010 0011 1010 0011
Alice’s photon state sequence ↔∪∩ ↔↔∩ ∪∩↔ ∪∪∩
Bob’s measurement basis choice ZXZX XZZX XZXX XXZZ
Bob’s measurement outcome (eigenvalue) +1 +1 −1 −1 +1 −1 +1+ 1 −1 −1+1+1 −1 −1 −1 +1
Bob’s measurement outcome (bit) 1 100 1 0 11 001 1 000 1
Bob’s next move is to communicate to Alice, using a public channel like telephone or
email, not the bits he has measured, but his measurement-basis sequence, namely from
Table 25.8:
ZXZX XZZX XZXX XXZZ.
Such information will tell Alice Bob’s right choices in the measurement, since she is the
only one to know how she has coded the photon polarizations. She then uses the same
public channel to give Bob her answer, which comes in the form:
YesNoNoYes NoYesNoNo NoNoYesNo YesYesNoYes.
This information tells Bob where his measurements were right and, therefore, which
information bits are valid and which other ones are to be discarded.
19
Thus, Bob and
Alice keep as valid the following bit sequence (− meaning discarded bit):
1 −−0/ − 0 −−/ −−1 − /00 − 1 ≡ 1001001,
which amounts to nine valid bits altogether. Since the probability of Bob choosing
the right measurement basis is 50%, it is clear that for longer sequences Bob would
obtain about 50% valid bits. Thus, if Alice sends a 1000 bit sequence to Bob, the whole
operation will result in obtaining a valid bit sequence of a length of nearly 500 bits. Such
a sequence can then be used by both Alice and Bob as a shared secret key to encrypt
and decrypt messages over a public channel, using DES or AES cryptoalgorithms, for
instance.
20
19
Note that the same result can be obtained the other way around: over a public channel, Alice tells Bob
which bases she used to code each of the polarized photons, namely ZZXX ZZXZ ZXXZ XXXZ, and then
Bob tells Alice which of his measurements were right. What matters is that both Alice and Bob know which
bits are to be discarded in the sequence.
20
Here, I am not addressing the issue of photon loss due to effects such as atmospheric or fiber absorption.Put
simply, all photons must be generated within a certain time slot. The absence of photons in a given time slot
does not mean a measurement failure, but rather an absence of measurement (or a global, zero SPD
1
–SPD
2
count). It is a basic engineering issue to predict the probability that, given the link budget and the photon
generation and measurement apparatus used by Alice and Bob, a polarized photon is successfully measured
from either end. Alice and Bob, thus, have an accurate knowledge of the photon-transmission capability
of their link, namely, how many photons can be successfully transmitted on average. Hence, any observed
deviation from this communication quality immediately betrays any wiretapping action o n the link.

556 Classical and quantum cr yptography
One may wonder how “safe” the above-described key-distribution approach is. How
can Alice and Bob be certain that no malicious Eve is able to intercept the key? The
answer is, in fact, quite simple: there is no possibility whatsoever for Eve to eavesdrop
the key-distribution channel. The proof of this statement is also quite simple: photons
cannot be split. The photon communications channel is, therefore, reputed “absolutely
invulnerable,” according to this fundamental law of quantum mechanics. There are many
subtleties associated with such a concept of “invulnerability,” which I reserve for the
reader to the end, see Section 25.13.
25.10 The BB84 protocol for QKD
In this section, I describe the BB84 protocol, named after its inventors C. H. Bennet and
G. Brassard, and the year of publication, 1984. The description made in the previous
section is essentially that of the BB84 protocol. Here, it just needs to be formalized
further and generalized to any key sizes. Note that the role of Alice and Bob can be
interchanged, each one being capable of generating a QKD session, which is also a
potential means for authentication and other security tests.
Alice uses a random-bit generator to produce two sequences A = (a
1
, a
2
,...) and
B = (b
1
, b
2
,...), each of N =
(
4 +
)
n bits length, with being a small integer
number playing the role of a reserve, and 2n being the desired key length (the explanation
for the factor of two comes later). Then she produces an N -qubit block sequence
|
ψ
,
which can be expressed in the form:
|
ψ
=
ψ
a
1
b
1
⊗
ψ
a
2
b
2
⊗···⊗
ψ
a
N
b
N
≡
N
⊗
k=1
ψ
a
k
b
k
.
(25.24)
For each cbit pair a
k
, b
k
the corresponding single qubit
ψ
a
k
b
k
is generated according to
the following (possible) convention:
⎧
⎪
⎪
⎨
⎪
⎪
⎩
|
ψ
00
=
|
0
|
ψ
01
=
|
+
|
ψ
10
=
|
1
|
ψ
11
=
|
−
.
(25.25)
We observe that the random value of the bit b
k
determines the choice of either state,
|0, |+(or , ∩with polarized photons) to represent a
k
= 0, and the same with |1,
|
−
(or ↔, ∪ with polarized photons) to represent a
k
= 1. We may also state that b
k
= 0
encodes the a
k
bit in the quantum basis Z, and b
k
= 1 encodes the a
k
bit in the quantum
basis X . This generalizes the description made in the previous section.
The N -qubit block
|
ψ
is then input to the quantum communication channel by Alice,
and Bob receives the state ρ = ε
(
|
ψ
ψ
|
)
. Such a formulation recalls that the channel
is characterized by a quantum operation ε, which includes any effects such as quantum
noise and Eve’s wiretapping.
