Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

25.2 Encryption and decryption with binary numbers 527

possibilities. Yet the code was eventually cracked in 1932, again illustrating the unlimited

resource of human ingenuity!

A second historical turn in cryptography history was marked by t he advent of digital

computers and, hence, the possibility not only to substitute letter symbols into each other,

but to intermingle their bits, and intermingle all the bits of all plaintext symbols, notwith-

standing the extended keyboard alphabet of 2

= 256 ASCII word symbols. Moreover,

binary operations can be introduced (such as XOR and polynomial multiplication) to

make cryptanalysis even more intractable. These new classes of cryptosystem yield

ciphertexts under the form of near-perfect pseudo-random bit sequences, thus, betraying

no speciﬁc patterns or block frequencies on which previous cryptanalysis fed.

A third historical turn was marked by the invention of public-key cryptography or

PKC (see further), which is basically cryptography without key exchange. As we shall

see, the strength or conﬁdence in PKC is based on the difﬁculty of factorizing large

numbers into primes. But, as we already know, the difﬁculty could be alleviated, should

practical quantum computing be developed, with Shor’s factorization algorithm, which

was described in Chapter 20.

The above illustrates that the notion of cryptosystem invulnerability is all relative,

especially considering the power of s upercomputers and the ever-increasing sophistica-

tion of cryptanalysis.

25.2 Encryption and decryption with binary numbers

This section reviews the basics of what could be called “modern” cryptog raphy. As we

shall see, the principles used in modern cryptography are not just the same older ones

implemented with powerful computers and bigger keys, like “super-Enigma” machines.

Rather, and as mentioned earlier, they represent a third phase of history with the intro-

duction of new algorithms, leading to ciphers that are hopelessly hard to crack with

current-generation supercomputers. Although digital cryptography may appear a tricky

subject (and it really is!), the elementary basics are surprisingly simple to describe.

Here, I will ﬁrst look at how encryption and decryption work with binary numbers,from

simple transposition to more complex algorithms, which opened the way to modern

standards.

Alphanumeric characters, including spaces, punctuation, numbers, and other signs,

which we use as a written language, are seen by computers in the form of standard

binary-number codes. As mentioned earlier, the two main alphanumerical codes used in

computer communications are ASCII (American standard code for information inter-

change),

and its extension EBCDIC (extended binary coded decimal interchange code).

These two standard codes use seven-bit and eight-bit (one byte) words, respectively. The

Standard ASCII tables providing the corresponding alphanumeric/binary conversion can be found, for

instance, in:

http://en.wikipedia.org/wiki/ASCII,

www.webopedia.com/quick

ref/asciicode.asp,

www.neurophys.wisc.edu/comp/docs/ascii/.

528 Classical and quantum cr yptography

Table 25.1 Ciphering by switching bit positions by pairs.

PlaintextI mi ssyou

PT-ASCII 1001001 1101101 1101001 1110011 1110011 1111001 1101111 1110101

CT-ASCII 0110001 1110011 1110001 1101101 1101101 1111001 1110111 1101011

Ciphertext 1s qmmywk

Table 25.2 Ciphering by taking characters by pairs and s w apping their center bits.

PlaintextI mi s s you

PT-ASCII 1001001 1101101 1101001 1110011 1110011 1111001 1101111 1110101

CT-ASCII 1001001 1101101 1100001 1111011 1111011 1110001 1100111 1111101

Ciphertext Ima{{qg}

ASCII and EBCDIC codes have 2

=128 and 2

=256 possible alphanumerical charac-

ter and other keyboard-command possibilities, respectively. For cryptography purposes,

this represents a huge extension of the previous 26-letter alphabet from earlier times.

How to constr uct ciphers from binary-numbers? The answer is that there is an unlim-

ited number of ways to proceed, even i n the simplest cases. Instead of 26 symbol char-

acters, we now have only two symbols, namely 0 and 1. Since each group of seven bits

(ASCII) represents one plaintext character, there is a wide variety of possible schemes

for transposition, substitution, or permutations. The number of ways in which any single

seven-bit word can be modiﬁed into any other seven-bit word is 2

= 128, as opposed

to only 26 with the ordinary alphabet. But the interesting feature of the binary system

is that now we can code the bits not only within a single seven-bit block, but over the

entire message sequence, which scrambles the blocks between themselves. For instance,

the (four bit per character) sequence

...

can be transformed by switching the bit positions by pairs, which gives

...

Alternatively, we can take characters by pairs and swap their center bits, i.e., for ﬁve bit

per character sequences:

...

Clearly, the decryption algorithms consist of performing the reverse substitutions from

the above ciphertexts. Let us see now what these two approaches produce as cipher

texts (CT). Consider the example in Tables 25.1 and 25.2 (ASCII, seven-bit characters),

noting that we can now use capital characters in the alphabetical plaintext (PT).

In the ﬁrst case, we observe that the last bit (a

) of each character is unchanged (since

the number of bits is odd), and that the character y is invariant. In the second case,

the ﬁrst two characters, I and m, are invariant. But if we were to swap more bits up

25.2 Encryption and decryption with binary numbers 529

to a complete permutation algorithm, we would achieve most perfect scrambling. For

an eight-character or 56-bit codeword, the number of possible permutations is 56! =

7.1 × 10

, although with a sufﬁciently complex substitution algorithm, this approach

would seemingly yield undecipherable messages. But the drawback is that its key (the

scrambling algorithm) is ﬁxed once and for all. No matter how complex, a ﬁxed-key

cryptoalgorithm is, in fact, very vulnerable to attack. The key can be intercepted during

its communication (over the Internet, for instance) without the two parties being ever

aware of it. The key can be retrieved from the software used to encrypt or decrypt, should

one of the terminal computers be intruded by a t hird party. The alternative is to use a

different key (referred to as a one-time-pad cipher) for each new message. This means

that the two parties have agreed beforehand on a list of different keys (here, substitution

algorithms) to be used only once. This approach is not at all practical for any routine

use, such as in an army central command. If the list of keys is to be communicated over

the Internet (or any other wide-range transmission medium), or listed in a book (as in the

case of the Enigma machine), it is also extremely vulnerable. The solution to this issue,

which is not trivial, is to be addressed in the next two subsections. In the following, we

will prepare ourselves further by considering how secret keys can be used in the binar y

system.

In the binary system, a secret key is made of a single codeword of any desirable

length, which must remain known only to the two parties. In contrast, the encryption and

decryption algorithm can be known to anyone. If the secret key is to be memorized, so as

to leave no paper or computer-ﬁle trace of it, it must be plain English (or any language

for that matter); for instance, a “codeword,” a “passphrase” or even the ﬁrst paragraph

or page of a book text commonly used and secretly agreed on. In the last case, the key

may simply be the page number of the book, which is easy to memorize. By itself, this

requirement of easy memorization or that the key be in plain English represents a built-in

weakness, because it exposes the cryptosystem to frequency analysis. Nowadays, this is

no longer an issue, since random binary keys are used. The remaining issue is how to

safely exchange and renew such keys, which is discussed later.

Mixing the secret key with the plaintext provides a means for both encryption and

decryption. Such mixing is performed by simple Boolean operations. In the binary

system, the four operations, called Boolean, are NO (logical inversion), AND (multi-

plication), OR (addition or subtraction), and XOR (exclusive OR). The rules of these

operations on one (NO) or two (AND, OR, XOR) bits or “operands” have been intro-

duced in Chapter 15. We note that with binary numbers, addition and subtraction are

thesame(1+ 1 = 1–1= 0, 1 + 0 = 1–0= 0 + 1 = 0 − 1). We also note that

XOR is the same as OR, except for the rule 1 + 1 = 0, which is similar to 9 + 1 = 0

in the ordinary digital system. The operators (NO, AND, OR, and XOR) are also noted

by mathematicians ¬, ∧, ∨, and ⊕, respectively. Thus NO a, a AND b, and a XOR b

are noted ¬a, a ∧ b, and a ⊕ b, respectively. The other basic Boolean operators are ≤

(noted →) and =(noted ↔). Thus, a → b is zero if a > b, and one otherwise. Similarly,

a ↔ b is zero if a = b, and one if a =b. I t is easily checked that the binary result of the

operation

(

→ b

)

∧

(

b ↔ c

)

is unity if and only if the condition a ≤ b = c is fulﬁlled.

In this chapter, we will not be concerned by Boolean logic other than just using XOR.

530 Classical and quantum cr yptography

Table 25.3 Ciphering with the (case-sensitive) key sAXOPHON.

PlaintextI mi s s you

Key s AXOP HON

PT-ASCII 1001001 1101101 1101001 1110011 1110011 1111001 1101111 1110101

K-ASCII 1110011 1000001 1011000 1001111 1010000 1001000 1001111 1001110

CT-ASCII 0111010 0101100 0110001 0111100 0100011 0110001 0100000 0111011

Ciphertext ;‘1< # 1 space ;

An interesting property of XOR is that its double application to a with the same

operand b restores operand a, i.e., a ⊕ b ⊕ b = a. We can, thus, use this property for

the purpose of encryption with a key. Indeed, if we perform XOR between each bit of

the plaintext and the key, we obtain a ciphertext. If we repeat the operation, this time

between the ciphertext (CT) and the key (K), we obtain the plaintext ( PT). Table 25.3

shows an example, with sAXOPHON as a (case-sensitive) key.

We see from this example that the same ciphertext character may correspond to

different plaintext characters, namely the ;s corresponds to I and u and the 1s corresponds

to i and y, respectively. We may, therefore, rapidly conclude that this XOR operation

with a key as long as the plaintext (or sufﬁciently long and repeated) and as many as

128 possible characters would produce quite a strong cipher. But this is not the case. To

provide here a simple explanation, consider indeed the ﬁrst codeword of the ciphertext,

0111010. Because of the XOR operation, it is certain that

(1) For bit numbers 7, 3, and 1: the operands must be of the same parity, namely coming

from the operations 0 XOR 0 or 1 XOR 1;

(2) For bit numbers 6, 5, 4, and 2: the operands must be of opposite parities, namely,

coming from the operations 0 XOR 1 or 1 XOR 0.

Since there are two operand choices for each bit, the number of possibilities is 2

128. But we can reduce this number by correlating the two different conditions for each

bit. To establish such a correlation, we can tabulate all correspondence possibilities

between each seven-bit ciphertext block and key block in the f orm of a 128 × 128 =

16 384 element array, where the cases that violate the two conditions are left empty.

A straightforward frequency analysis of both plaintext and key, searching for the most

common letters, digrams, trigrams, and other most commonly used English words will

allow a small computer to ﬁnish the job in seconds! This description suggests that in the

binary system, encryption with a secret key on a one-to-one character basis is unsafe,

unless complex random keys are used.

As we saw earlier, the binary system offers a tremendous advantage, which is the

possibility of mingling the characters together in the coding process, on a bit-by-bit

or block-by-block basis (a block being a string of bits of any prescribed length). This

is the principle used by the ﬁrst attempt at a standard cipher, developed in the 1960s

by IBM and called Lucifer (as a pun on cipher). Figure 25.1 shows the Lucifer coding

procedure. In the ﬁrst step, the plaintext is converted into a string of binary digits

(not necessarily ASCII). Then the string is split into 64-bit blocks (step 2) which are

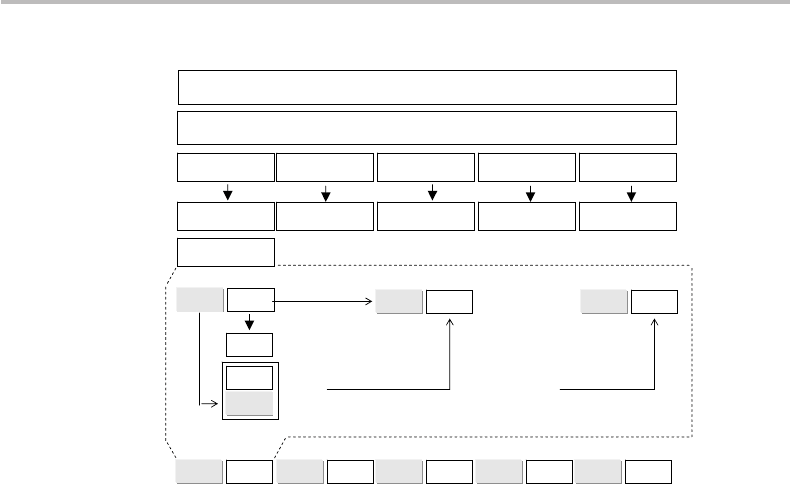
25.2 Encryption and decryption with binary numbers 531

Plaintext

1100101011100010111101000101011110110001

Step 1

11001010

Step 2

11100010 11110100

01010111

10110001

01000100

10100111

10100010 11111101

01011000

Step 3

00100001

Step 4

Step 5

0010 0001

Left

Right

Step 6

0110

XOR

0010

0001 1110

Left

Right

Round 1

1010 0111

Left

Right

Round 16

...

1010 0111

Left

Right

1101 1111 1001 0100 1110 0110 0000 1001

Cipher

Figure 25.1 Principle of the Lucifer encryption algorithm, as described in the text.

individually encrypted (step 3). The resulting blocks are shufﬂed (step 4), then split into

two 32-bit elements called left

and right

(step 5). The next step is called a round,

and this round will be repeated sixteen times. Call these two elements L0 and R0,

respectively. The round ﬁrst passes R0 through a mangler, which performs a complex

bit substitution according to a mangling function. The result is XORed with L0 to give

R1. The original R0 becomes L1. The next round does the same with the pair (L1, R1),

and so on until one gets (L16, R16). The cipher is then formed with the concatenated

string of (L16, R16) elements.

We see that this new approach for encryption is quite complex and deﬁnitely harder

to break than any previous scheme. Even with public knowledge of the encryption

algorithm, the code breaker must know which mangling function (the key) has been

used for the 16 rounds, which shufﬂing algorithm is used in step 4, and which encryp-

tion algorithm is used in step 3. The combination of these three unknowns presents a

formidable obstacle to code-breaking attempts. But when these different elements are

known, decryption is “straightforward” for any computer. The cipher is decomposed into

32-bit block pairs representing as many L16, R16 groups. The element L16 becomes

R15. The element R16 is then XORed with L15, then the result is passed through the

inverse mangling function (the key), which yields R15. And so on until L0 and R0 are

obtained. The L0 and R0 elements are then concatenated into a 64-bit block.

The bits are then reordered, according to the inverse of the shufﬂing algorithm.

The resulting block is decrypted. Then all decrypted blocks are concatenated together

and converted into plaintext. We can infer that the whole decrypting operation can be

performed in a few milliseconds of computer time, depending on the complexity of

the step-3 cipher and the mangling function. As I have stated it, the mangling function

represents the key to the encryption and decryption process. Such a key can be deﬁned by

532 Classical and quantum cr yptography

a number, which represents the different integer parameters to be used for generating the

mangling function. Thus, the number of possible keys is virtually inﬁnite. To prevent any

possibility that this code became absolutely unbreakable, it was agreed that the number

of keys should be 2

≈ 72 × 10

, which corresponds to a 56-bit key. Twenty-ﬁve years

later, the principle of the Lucifer system with a 56-bit key was ofﬁcially endorsed in the

USA to become the data encryption standard (DES), which is still widely in use today,

albeit superseded by its own variants and other standards, such as AES (see fur ther).

25.3 Double-key encryption

In spite of the tremendous levels of protection offered by algorithms like DES and

Lucifer, a major weakness remains, which is the obligation for the originator to com-

municate the key to the destinee. Like the Germans with Enigma, both parties could

keep a secret copy of the same book, where the key to be used is indicated for each

day of a month or year. A new set of books must be created and exchanged on this

monthly or yearly basis. But a malicious third party may intercept the book and rapidly

copy the contents, while making sure that no one notices anything. As a result, all secret

communications based on this book’s keys could be read “in the open” by this third

party, the worst being that the two ends are unaware of it.

In cryptography, the tradition has it to call the originator Alice and the destinee Bob.

The malicious interceptor, who eavesdrops, is Eve. From this point, I will use these three

nicknames. For Alice, the encryption task is like putting a message into a locked steel

box and sending it to Bob through the mail. If Bob does not have a copy of Alice’s key

to open the lock, then he can’t retrieve Alice’s message. Alice must then provide Bob a

copy of her key, for instance by meeting regularly in some agreed time and place. But

this way of proceeding amounts to the same thing as passing on and hiding key books,

notwithstanding the time and effort required.

This intractable problem of key exchange caused cryptographers to search for new

directions in the way message “boxes” could be locked and unlocked. They found that

one simple solution could be to use two locks instead of one! To visualize how this can

work, assume that both Alice and Bob have different keys of their own. Alice locks her

message box and sends it to Bob (step 1). Bob cannot open it, since he does not have

Alice’s key. What he does is to put a second lock on the box, lock it with his own key,

and send the box back to Alice (step 2). Then Alice opens the ﬁrst lock with her key. She

then sends back the box to Bob (step 3). Now Bob can open the box, since he has the key

of the remaining lock (step 4). Such a process is referred to as double-key encryption.

The remarkable result is that the message is safely communicated without Alice and

Bob exchanging any key whatsoever. Consider now a practical illustration. Table 25.4

shows the different steps of double-key encryption, using the principle of adding (XOR)

a same-length key (since the purpose is just to prove the point through successive XOR

additions, I have chosen random keys for Alice and Bob).

We see from the above example that at the end of this double-key encr yption process,

Bob is able to retrieve the plaintext unaltered (step 4). We note again that in the different

25.3 Double-key encryption 533

Table 25.4 Double-key encryption.

PlaintextI mi s s you

PT 1001001 1101101 1101001 1110011 1110011 1111001 1101111 1110101

Alice’s key 0001001 1010100 0101011 0111101 0111010 0001001 1001001 1100100

Step 1 1000000 0111001 1000010 1001110 1001001 1110000 0100110 0010001

Bob’s key 1011001 1000111 0111010 1111101 0101110 0011001 1001000 0001011

Step 2 0011001 1111110 1111000 0110011 1100111 1101001 1101110 0011010

Alice’s key 0001001 1010100 0101011 0111101 0111010 0001001 1001001 1100100

Step 3 0010000 0101010 1010011 0001110 1011101 1100000 0100111 1111110

Bob’s key 1011001 1000111 0111010 1111101 0101110 0011001 1001000 0001011

Step 4 1001001 1101101 1101001 1110011 1110011 1111001 1101111 1110101

Plaintext I mi s s you

Table 25.5 Intercepting the message in Table 25.4.

Step 1 1000000 0111001 1000010 1001110 1001001 1110000 0100110 0010001

Step 2 0011001 1111110 1111000 0110011 1100111 1101001 1101110 0011010

XOR 1011001 1000111 0111010 1111101 0101110 0011001 1001000 0001011

Step 3 0010000 0101010 1010011 0001110 1011101 1100000 0100111 1111110

XOR 1001001 1101101 1101001 1110011 1110011 1111001 1101111 1110101

Plaintext I mi s s you

steps, Alice and Bob only used their own keys. The explanation of this successful

retrieval is the following. Call M the plaintext message block and A, B the keys from

Alice and Bob. The cipher in step 1 is, thus, M XOR A,orM ⊕ A. The cipher in

step 2 is M ⊕ A ⊕ B. That in step 3 is M ⊕ A ⊕ B ⊕ A = M ⊕ B (using the above-

described property of XOR). Finally, the result in step 4 is M ⊕ B ⊕ B = M, which is

the plaintext.

While the previous double-key encryption surely works without any key exchange, it

is absolutely unsafe! Indeed, if Eve is ever able to intercept all three messages (ciphers

in step 1, step 2, and step 3 in the above), the only thing she has to do to retrieve the

plaintext is to XOR these together, as shown in Table 25.5.

There is nothing surprising in this result if we consider from the previous deﬁnitions

that what Eve does is the operation

(M ⊕ A) ⊕ (M ⊕ A ⊕ B) ⊕ (M ⊕ B) = M ⊕ M ⊕ M = M.

Since Eve can so effortlessly retrieve the plaintext, without even any cryptanalysis, we

conclude that this “no key exchange” approach based on the addition of independent

keywords is, by and large, the worst possible and riskiest way to proceed.

A safer solution for Alice and Bob could consist in using substitution algorithms

instead. But the problem is that substitution algorithms have no reason to be commutative.

If Alice ﬁrst encrypts the message with her own substitution-key algorithm, then Bob

does the same with his own, and then Alice and Bob again, the end result would be

534 Classical and quantum cr yptography

nonsense. A fancier approach had to be devised, which led to the breakthroughs of

cryptography without key exchange, and public-key cryptography (PKC), which are

described in the next two subsections.

25.4 Cryptography without key exchange

The seemingly intractable problem of cryptography without key exchange was eventually

solved in the mid 1970s. The ground-breaking idea was to use the principle of one-way

functions in modular arithmetic. Here is the ﬁrst proposed algorithm (now referred to as

Difﬁe–Hellman or Difﬁe–Hellman–Merkle, after the inventors).

Step 0 Alice and Bob call each other (or send an email) to agree on a choice of two

numbers (m, n), regardless of the possibility that Eve could have wired the line;

they can even make this choice openly public.

Step 1 Alice chooses a large integer A and keeps it secret. Then she computes

a = m

mod n

and sends the result (e.g., by phone or email) to Bob.

Step 2 Bob chooses a large integer B and keeps it secret. Then he computes

b = m

mod n

and sends the result (e.g., by phone or email) to Alice;

Step 3 At her end, Alice computes

k = b

mod n.

Step 4 At his end, Bob computes



= a

mod n.

As it turns out, the results of these last two computations are equal, i.e., k = k



= m

(modulo n). This means that both Alice and Bob have the same number, which they can

use as a common key. Eve is not able to get this information, even if she has intercepted

the information on the (a, b) values that Alice and Bob communicated to each other.

Although Eve also knows m, n, she has no clue as to the exponent AB of the key. And

since Alice and Bob chose large secret numbers, AB is also very large! For instance, if

A and B are of the order of 1000, the exponent of the key is of the order of 1 000 000,

representing a 20-bit key in the binary system. They might as well choose numbers in

the order of 10 000, which generate 100 000 000 different key possibilities (26-bit key).

Note that from Alice’s or Bob’s ends, the whole procedure actually involves only two

steps (1 and 3 and 2 and 4, respectively), which I have decomposed here for clarity.

It is completely remarkable and counterintuitive that two persons can mutually agree

on a secret key by openly exchanging information via a public communication channel

(even an eavesdropped line!) without this secret ever being known. The Difﬁe–Hellman–

Merkle algorithm of “key generation without key exchange” can even be generalized to

25.4 Cryptography without key exchange 535

parties of three or more. Consider the following sequence with Alice, Bob, and Cindy,

now grouped into simultaneous steps:

Step 1 Alice chooses a large integer number A and keeps it secret; she computes

a = m

mod n and sends the result to Bob;

Bob chooses a large integer number B and keeps it secret; he computes b =

mod n and sends the result to Cindy;

Cindy chooses a large integer number C and keeps it secret; she computes

c = m

mod n and sends the result to Alice.

Step 2 Alice computes c



= c

mod n and sends the result to Bob;

Bob computes a



= a

mod n and sends the result to Cindy;

Cindy computes b



= b

mod n and sends the result to Alice.

Step 3 Alice computes k = (b



)

mod n;

Bob computes k



= (c



)

mod n;

Cindy computes k = (a



)

mod n.

As immediately checked, the three results k, k



, k



, computed separately by Alice, Bob,

and Cindy, are all identical to m

ABC

, which now represents their secret key. Note that the

initial secret numbers A, B, C don’t need to be as large as in the previous case. Numbers

of the order of 1000 generate as many as 1 billion keys. But there is no reason not to use

greater numbers to give a trillion possibilities.

Here is another variant of the Difﬁe–Hellman–Merkle algorithm (referred to as

Hughes), where Alice wants the secret key to be some speciﬁc number, k.

Step 1 Alice chooses a large integer number A and keeps it secret; she computes

k = m

mod n.

Step 2 Bob chooses a large integer number B and keeps it secret; he computes

b = m

mod n

and sends the result to Alice.

Step 3 Alice computes

a = b

mod n

and sends the result to Bob.

Step 3 Bob computes

c = 1/B

and



= a

mod n.

The result of Bob’s operation is k



= a

1/B

= a

1/B

= (b

)

1/B

= (m

)

1/B

= m

= k

(modulo n). Thus, Alice has successfully communicated her preferred key choice to

Bob. The advantage of the Hughes algorithm is that Alice can initiate the communication

536 Classical and quantum cr yptography

of encrypted messages herself, not only to Bob but to any g r oup of persons. She can

send them the key at a later time.

These approaches concern secret-key cryptography, which, except for the absence of

key exchange, resor t to the same classical approach when it comes to encryption and

decryption. Furthermore, the two parties share the same (secret) key, therefore, they can

both encrypt and decrypt with that key. In the communication channel, their relationship

is symmetric, hence, the name symmetric-key cryptography. An interesting alter native

would be to have different keys for encryption and decryption: Bob can send Alice

encrypted messages using a shared key, but only Alice is able to decrypt them, using

her own secret key. Bob’s and Alice’s communication being, thus, asymmetric, they are

using a new form of asymmetric-key cryptography. In the next section, we shall see

that modular arithmetic opened the path to asymmetric cryptography, better known as

public-key cryptography (PKC).

25.5 Public-key cryptography and RSA

The approach of public-key cryptography (PKC) led to the RSA standard, named after

its inventors R. Rivest, A. Shamir, and L. Adleman. A detailed description of PKC and

RSA was presented in Chapter 20 concerning Shor’s (quantum) factorization algorithm,

along with modular-algebra basics shown in Appendix T. The reason for describing PKC

and RSA in that earlier chapter is to illustrate that the cryptoalgorithm would be readily

“cracked” overnight should, one day, Shor’s factorization be successfully implemented

in quantum computers. Fortunately for PKC and RSA, such a horizon still lies in the

far distant future, but in the timescale of cryptology, how “distant” is that? Here, I

assume that the reader is already familiar with PKC and RSA, or will refer back to

Chapter 20 and, therefore, I shall only f urther develop the discussion about factorizing

large numbers.

The PKC and RSA cryptosystem is, indeed, based on the fact that it is extremely

difﬁcult to factorize large numbers. To recall, given a number n, factorization consists

of ﬁnding the unique set of prime numbers ( p

, p

,..., p

) whose product p

× p

...× p

is equal to n. Note that these prime factors are not generally all different. For

instance, the number 1000 is factorized into 2 × 2 × 2 × 5 × 5 × 5 = 2

× 5

. We can

then use just two sufﬁciently large and different prime numbers ( p, q) to generate a

bigger number n = pq, knowing that someone who knows n would have a hard time

ﬁguring out the t wo primes ( p, q), and this is basically the essence of the PKC and RSA

safety assumption. For instance, consider n = 62 615 533. To ﬁnd its factorization, we

need to divide it by prime numbers, trying them out one after another. In this speciﬁc

case, the answer is p =7919 and q = 7907, which are the highest two primes in the ﬁrst-

thousand prime list.

This choice made factorization easy with any pocket calculator.

See lists of the ﬁrst 1000 primes in, for instance:

http://primes.utm.edu/lists/small/1000.txt