Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


24.2 Shor code 507
Table 24.3 Corrective actions in Shor code from bit-
flip syndrome diagnostic based on measurements of
(
Z
12
, Z
23
)
in entangled 3-qubit block U, and the prin-
ciple of majority logic.
Z
12
U
Z
23
U
Corrective action
1 1 None
1 −1 Flip 3rd qubit
−1 1 Flip 1st qubit
−1 −1 Flip 2nd qubit
syndrome measurements! Next, we can apply Z
23
on block U to obtain, in turn:
Z
23
+
+
+
ˆ
ˆ
0
/
U
=
[
I ⊗
(
|0000|+|1111|
)
− I ⊗
(
|0101|+|1010|
)
]
|010+|101
√
2
=
I ⊗|0000|
|010+|101
√
2
+ I ⊗|1111|
|010+|101
√
2
− I ⊗|0101|
|010+|101
√
2
− I ⊗|1010|
|010+|101
√
2
= 0 + 0 −
|101
√
2
−
|010
√
2
≡−
|101+|010
√
2
≡ Z
12
+
+
+
ˆ
ˆ
0
/
U
.
(24.29)
Hence, the measurement
Z
23
U
=Z
12
U
≡−1. (24.30)
The above two measurements, each yielding −1, are sufficient to diagnose that the
second qubit in block U is corrupted. If we are not convinced, we may perform a third
measurement with Z
13
, which, according to expectation, will yield +1 (this being left
as an exercise). Such a result indicates that the first and third qubits are the same, which
confirms the previous diagnostic. Table 24.3 summarizes the different diagnostic and
corrective action possibilities in the general case. Clearly, the complete diagnostic and
error-correction procedure requires one to perform the two comparative measurements
Z
12
, Z
23
on each of the three blocks A, B, C, representing altogether six measurements
and 4
3
= 64 possible bit-flip error diagnostics. It is also clear that a bit flip error occurring
on any block U of |
ˆ
ˆ
0 replicates on the same block U of |
ˆ
ˆ
1 (observing from Eq. (24.23)
that these two blocks only differ by their relative phase factor).
The above description concerned the detection and correction of either phase-flip or
bit-flip errors occurring in the encoded 9-qubits |
ˆ
ˆ
0 and |
ˆ
ˆ
1. It is clear that since the
syndrome measurements leave the qubit invariant, both error types can be corrected in

508 Quantum error correction
any order. What about error correction on encoded 9-qubits of the form
+
+
+
ˆ
ˆ
q
/
= α
+
+
+
ˆ
ˆ
0
/
+ β
+
+
+
ˆ
ˆ
1
/
, (24.31)
corresponding to an originator message |q=α|0+β|1? To answer this question, we
may first define the channel output qubit as
+
+
+
ˆ
ˆ
q
/
= α
+
+
+
ˆ
ˆ
0
/
+ β
+
+
+
ˆ
ˆ
1
/
. (24.32)
As we have seen earlier, the phase-flip syndrome diagnosis consists of making two
successive measurements of the type (ijklmn = 123456, 123789, 456789):
C
X
ijklmn
=
=
.
ˆ
ˆ
q
+
+
+
X
ijklmn
+
+
+
ˆ
ˆ
q
/
=
#
¯α
.
ˆ
ˆ
0
+
+
+
+
¯
β
.
ˆ
ˆ
1
+
+
+
$
X
ijklmn
#
α
+
+
+
ˆ
ˆ
0
/
+ β
+
+
+
ˆ
ˆ
1
/$
=
|
α
|
2
.
ˆ
ˆ
0
+
+
+
X
ijklmn
+
+
+
ˆ
ˆ
0
/
+ ¯αβ
.
ˆ
ˆ
0
+
+
+
X
ijklmn
+
+
+
ˆ
ˆ
1
/
+α
¯
β
.
ˆ
ˆ
1
+
+
+
X
ijklmn
+
+
+
ˆ
ˆ
0
/
+
|
β
|
2
.
ˆ
ˆ
1
+
+
+
X
ijklmn
+
+
+
ˆ
ˆ
1
/
≡
|
α
|
2
.
ˆ
ˆ
0
+
+
+
X
ijklmn
+
+
+
ˆ
ˆ
0
/
+
|
β
|
2
.
ˆ
ˆ
1
+
+
+
X
ijklmn
+
+
+
ˆ
ˆ
1
/
≡±1. (24.33)
In the above result, we first used the property that the measurement X
ijklmn
leaves
the state invariant, therefore, the nondiagonal elements in the right-hand side in Eq.
(24.33) are zero. Since the same phase-flip error must be found in the two qubits |
ˆ
ˆ
0
and |
ˆ
ˆ
1
, the two nonzero matrix elements must be equal, and considering the property
|
α
|
2
+
|
β
|
2
= 1, we finally have X
ijklmn
=±1, corresponding to no (+1) or one (−1)
phase-flip error between the blocks A, B. Thus, syndrome diagnostic and error correction
can be implemented on the encoded qubit |
ˆ
ˆ
q
=α|
ˆ
ˆ
0
+β|
ˆ
ˆ
1
in exactly the same way
as described earlier for the qubits |
ˆ
ˆ
0
and |
ˆ
ˆ
1
. Clearly, the same conclusion applies to
the case of bit-flip errors with two successive measurements Z
ij
(ij = 12, 23, 13) on
the individual blocks U = A, B, C, yielding measurement outcomes Z
ij
U
=±1. The
key conclusion is that the Shor code can be implemented to correct both phase-flip and
bit-flip errors on any qubit of the general form |q=α|0+β|1.
The powerful error-correction capability of the Shor code does not end here. Indeed,
we may conceive of this code as being able to correct a true continuum of error events,
while simply using the discrete set of the above-described syndrome operators!
To show, this recall from Chapter 23 that a noisy quantum channel can be described
by a trace-preserving quantum operation ε of the form
ε(ρ
M
) =
k
U
+
k
ρ
M
U
k
, (24.34)
which is referred to as its operator-sum representation. In this definition,
ρ
M
=|ψ
M
ψ
M
|is the originator message density matrix, which most generally is an nth

24.3 Calderbank–Shor–Steine (CSS) codes 509
tensor product of symbol states ρ
i
=|q
i
q
i
| selected from a qubit symbol alphabet
{|q
i
}. The operators U
k
, called channel-operator elements, are responsible for vari-
ous sources of noise impairment. For single qubits (ρ
i
), the operator elements take
the form: U
1
=
√
p
1
X for the bit-flip channel, U
2
=
√
p
2
Z for the phase-flip channel,
U
3
=
√
p
3
Y for the bit-phase-flip channel, and U
0
=
√
p
0
I =
√
1 − p
1
− p
2
− p
3
I for
the noiseless channel, with {p
n
}representing the corresponding probability distribution.
We may define U
ki
as the operator of noise-type k acting on the qubit i in the Shor
codeword |
ˆ
ˆ
q. Thus, we have:
|
ˆ
ˆ
q
i
=
k
U
ki
|
ˆ
ˆ
q
i
=
(
p
0i
I
i
+ p
1i
X
i
+ p
2i
Z
i
+ p
3i
Y
i
)
|
ˆ
ˆ
q
i
,
(24.35)
with {p
ni
}being the corresponding probability distribution. We observe that through the
weighted action of the operator I, X, Y, Z , the above-defined quantum channel defines
a continuous qubit transformation onto the Bloch sphere. As we have seen, the Shor
code makes it possible to perform syndrome diagnosis and corrections onto any discrete,
single-error type, as caused by the operator elements U
ki
. Therefore, any qubit passed
through this channel, and corrupted by an “error continuum,” can be effectively restored
in its full original integrity. This remarkable property has no counterpart in the classical
world of error-correction codes.
24.3 Calderbank–Shor–Steine (CSS) codes
In this section, I describe a new class of quantum error-correction codes referred to as
the Calderbank–Shor–Steine (CSS) codes, which have the capability of correcting up
to t bit-flip and phase-flip qubit errors. The construction of CSS codes is based on the
use of two classical linear block codes, as described in Chapter 11. To recall, a linear
block code C is defined as a set (n, k)of
|
C
|
= 2
k
codewords x of bit length n.Itis
characterized by:
1
(i) A generator matrix G, of dimension n × k, which, for any n-vector z to be encoded,
yields the corresponding codeword x = Gz;
(ii) A parity-check matrix H , of dimension n × (n − k), which satisfies Hx = 0 for all
codewords x ∈ C.
Let (n, k
1
) and (n, k
2
), with k
1
> k
2
define two linear block codes C
1
, C
2
of sizes
|C
2
| < |C
1
|. To construct a CSS code, we require the following two conditions:
(a) C
2
⊂ C
1
: all codewords of C
2
belong to C
1
;
(b) C
1
and C
⊥
2
have a bit-error correction capability of t.
1
In Chapter 11,weusedtheleft vector-matrix multiplication y
T
U,wherey
T
is a line vector, instead of the
right vector-matrix multiplication Uy,wherey is a column vector, which is only a matter of convention.
Also we previously called x the vectors to be encoded and y the resulting codewords, while in this chapter
we shall use x and y to designate codewords from two different linear block codes.

510 Quantum error correction
In condition (b), C
⊥
2
is called the dual of C
2
. Given a block code with G, H as generator
and parity-check matrices, respectively, the dual of C, noted C
⊥
, is a unique block code
having H
T
, G
T
for generator and parity-check matrices, respectively (the matrix U
T
is
the transposed matrix of U).
Given two linear block codes C
1
, C
2
satisfying the above conditions, we can construct
a CSS code as follows. Let x, y be two n-bit codewords, such that x ∈ C
1
and y ∈ C
2
.It
is possible to define a quantum state |x + y, where + indicates here bit-wise addition
modulo 2 (or in Boolean logic, the exclusive OR, noted ⊕). For instance, if x = 00101
and y = 10111, we have |x + y=|10010. With such a definition at hand, given x ∈ C
1
we are able to construct all possible quantum states |x + y with y ∈ C
2
as well as the
normalized sum:
|
x + C
2
≡
1
√
|
C
2
|
y∈C
2
|
x + y
. (24.36)
Given the number 2
k
1
=|C
1
|of codewords x in C
1
, how many orthogonal quantum states
|x + C
2
can be, thus, generated? The answer to this question is |C
1
|/|C
2
|=2
k
1
−k
2
,
which stems from group theory (GT) and the fine notion of cosets.
2
Here, I shall not
venture into GT, but leave it as an interesting exercise to establish that the C = (7, 4)
Hamming code, (described in Chapter 11) forms a group (C, ⊕) under the bit-wise
addition ⊕ and to make the inventory of its various cosets.
A key property is that any element x ∈ C
1
must belong to one and only one coset of
C
2
. The same coset x +C
2
= x
+C
2
corresponds to two different elements x, x
∈ C
1
satisfying the property x − x
∈ C
2
and, hence |x + C
2
=|x
+ C
2
.
3
It is clear that
if two different elements x, x
∈ C
1
do not belong to the same coset (x + C
2
= x
+
2
I provide here a simplified description of cosets, which also explains the notation x +C
2
. First, it is impor-
tant to be familiar with, or to quickly revisit the basics of groups and subgroups, for instance through the
links: http://en.wikipedia.org/wiki/Group_%28mathematics%29, http://en.wikipedia.org/wiki/Subgroup.
Then assume two commutative groups C
1
and C
2
with additive operation +, such that C
2
⊂ C
1
is a
subgroup of C
1
. The cosets of C
2
in C
1
, noted x
i
+C
2
, are defined for all elements x
i
∈ C
1
as follows
x
i
+C
2
≡
x
i
+ y
j
y
j
∈C
2
.
Taking an illustrative example, assume C
1
= (0, 1, 2, 3), with + representing the addition modulo 4, and
which has the only “nontrivial” subgroup C
2
= (0, 2). The cosets of C
2
in C
1
are
0 +C
2
≡ (0, 2) = C
2
1 +C
2
≡ (1, 3)
2 +C
2
≡ (2, 0) = (0, 2) = C
2
3 +C
2
≡ (3, 1) = (1, 3) = 1 +C
2
.
It is seen that there are two distinct cosets of C
2
in C
1
, including C
2
itself, which are (0, 2) and (1, 3).
In the general case with groups and subgroups of finite sizes |C
1
|, |C
2
|, Lagrange’s theorem states
that the number of cosets is given by the ratio |C
1
|/|C
2
|. See also http://en.wikipedia.org/wiki/Coset,
http://en.wikipedia.org/wiki/Lagrange%27s_theorem_%28group_theory%29, and Exercise (24.4), which
studies the (7, 4) Hamming code as a group under the bit-wise addition operation.
3
Indeed, taking into account that 0 ∈ C
2
(C
2
is a subgroup with the identity element under ⊕) and assuming
x − x
∈ C
2
,wehave
x + C
2
={x + 0, x + (x − x
),...}={x, x
,...}
x
+C
2
={x
+ 0, x
+ (x − x
),...}={x
, x,...},

24.3 Calderbank–Shor–Steine (CSS) codes 511
C
2
) there is no y, y
∈ C
2
such that x + y = x
+ y
and, therefore, |x + C
2
must be
orthogonal to |x
+C
2
. Based on GT, the number of distinct cosets is |C
1
|/|C
2
|, hence
the quantum space spanned by the states |x + C
2
, as generated from the codewords
x ∈ C
1
, has a dimension |C
1
|/|C
2
|=2
k
1
−k
2
. This quantum space corresponds to a new
class of quantum code, noted CSS(C
1
, C
2
), which is to be pronounced, “CSS code of
C
1
over C
2
.”
Next, I shall describe how the CSS(C
1
, C
2
) code can correct up to t bit-flip (X) and
phase-flip (Z ) errors. Just as in the classical ECC case, the signature of errors, whether
of the X -orZ-type, is an n-vector with 1 s indicating the position where any error
occurred. Define e
X
and e
Y
as the corresponding vectors. If x is an n-bit codeword
and |x the corresponding quantum state, the applications of the combined error pattern
e
X
, e
Y
shall transform the state |x into the errored state |x
∗
according to:
|x
∗
=(−1)
x·e
Y
|x + e
X
, (24.37)
where x · e
Y
is the dot product of x and e
Y
. For instance, |x=|10011, e
X
=
(0, 1, 0, 1, 0) (X errors on the second and fourth qubits) and e
Y
= (1, 0, 0, 1, 1) (Z
errors on the first and last two qubits) yield x · e
Y
= 1.1 + 0.0 +0.0 +1.1 +1.1 ≡ 3
and |x + e
X
=|1 +0|0 +1|0 +0|1 +1|1 +0≡|11001, and the errored state
|x
∗
=(−1)
3
|11001≡−|11001. When the error pattern e
X
, e
Y
is applied to the CSS
codeword |x + C
2
defined in Eq. (24.36), the resulting errored state is
|(x + C
2
)
∗
≡
1
√
|
C
2
|
y∈C
2
(
−1
)
(
x+y
)
·e
Y
|
x + y + e
X
. (24.38)
The next step consists of the introduction of the parity-check matrix
˜
H to detect the t
errors of the X type (not to be confused here with the Hadamard gate H ). This is achieved
by appending an n-qubit ancilla |0 to the recipient’s codeword |x
∗
=|x + e
X
, and
passing the result through a quantum circuit that achieves the transformation |x
∗
|0→
|x
∗
|
˜
Hx
∗
. Recall from Chapter 11 that if x is a codeword, then
˜
Hx = 0, and hence
|
˜
Hx
∗
=|
˜
H(x + e
X
)≡|
˜
He
X
. Measuring each of the qubits in the ancilla |
˜
He
X
yields the syndrome vector
˜
He
X
and, hence, the full error diagnosis e
X
, which is
common to each of the series terms in Eq. (24.38). The ancilla can then be discarded
and each of the errored qubits can be corrected (or back flipped) by applying X gates in
the corresponding circuit wires, to obtain the X -corrected state
+
+
(
x + C
2
)
∗
=
X
≡
1
√
|
C
2
|
y∈C
2
(
−1
)
(
x+y
)
·e
Y
|
x + y
. (24.39)
A quantum circuit performing the operation |z|0→|z|Uz for any n × n matrix
U (here with U ≡
˜
H and
|
z
≡|(x + C
2
)
∗
) can be realized by exclusively using
CCNOT (controlled-CNOT) gates, as illustrated in Fig. 24.5. The design concept of
such a circuit can be grasped by analyzing the basic functionality
|
z
→
|
Uz
with U
where we used the (equivalent) bit-wise addition properties x + x = 0andx
=−x
. The same result is
obtained with the assumption x + x
∈ C
2
. It shows that the cosets x + C
2
and x
+C
2
have two elements
in common, which necessarily implies that x + C
2
= x
+C
2
and, hence, |x + C
2
=|x
+C
2
.
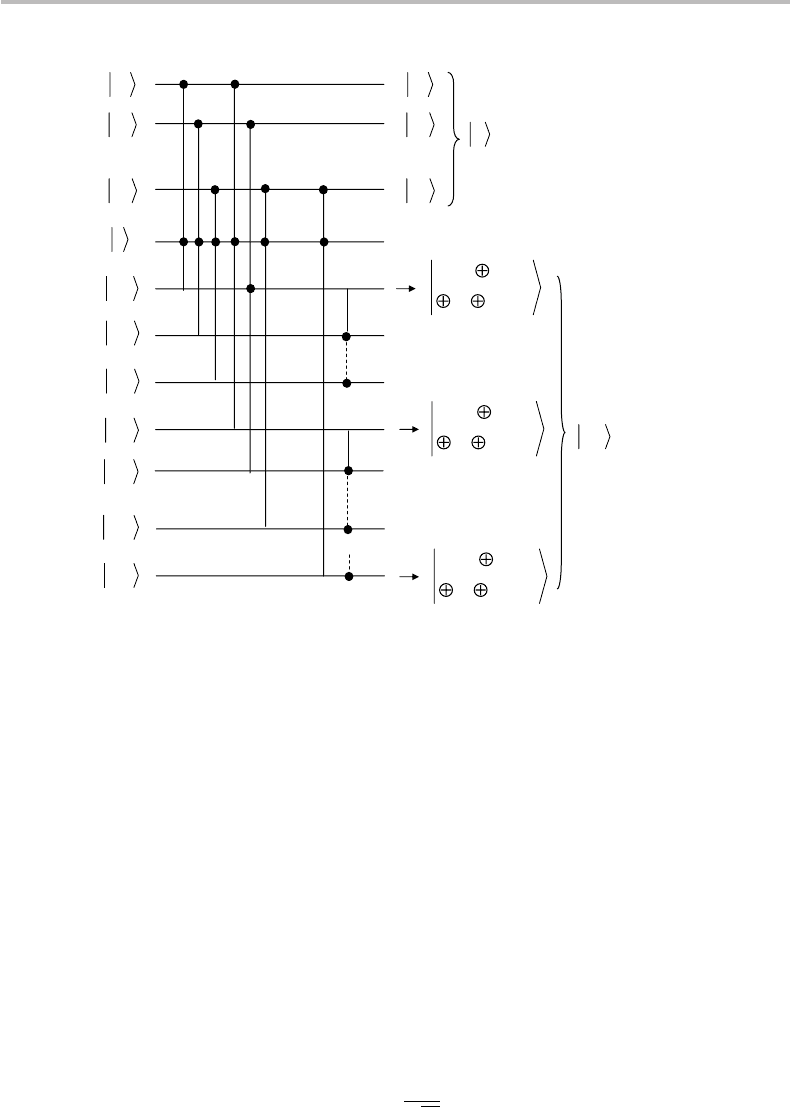
512 Quantum error correction
11
u
12
u
n
u
1
21
u
1
1
z
2
z
x
nn
zu
zuzu
1
2
12
111
...
x
x
x
z
Uz
n
z
…
1
z
2
z
n
z
n
u
2
nn
u
…
…
x
x
x
22
u
……
x
nn
zu
zuzu
2
2
221
21
...
n
nn
n
n
zu
zu
z
u
...
22
1
1
x
…
Figure 24.5 Quantum circuit to achieve the transformation
|
z
|0→
|
z
|
Uz
, given an n-qubit
|z and an n × n matrix U with binary coefficients.
being a 2 ×2 matrix with binary coefficients, which is left as an interesting exercise.
The figure actually shows that the binary coefficients u
ij
= 0, 1ofU can be directly
used as corresponding ancilla qubits |u
ij
=|0, |1, with the input state of the circuit
being
|
z
|1|u
11
...u
1n
|u
21
...u
2n
...|u
n1
...u
nn
. After discarding the useless (or
“garbage”) computation qubits, the circuit output is indeed |z
|
Uz
. To summarize, we
have shown that the CSS(C
1
, C
2
) code can correct all t errors of the X type, as allowed by
the C
1
linear block code, and the syndromes |
˜
He
X
and
˜
He
X
, can be generated through
a basic quantum circuit of CCNOT gates (Fig. 24.5), followed by the corresponding
qubit measurements and bit-flip corrections.
The correction of phase-flip, or Z -type errors, is achieved by first passing each qubit
of the X-corrected state |(x + C
2
)
∗
X
through a Hadamard gate, i.e., to obtain the state
H
⊗n
|(x + C
2
)
∗
X
.InChapter 19, when describing the Deutsch–Joszsa algorithm,we
have established (as supported through Exercise 19.1) that the action of H
⊗n
on any
n-qubit |x yields the transformation
H
⊗n
|x=
1
√
2
n
z
(−1)
z·x
|
z
, (24.40)
where z is any possible n-bit combination. Applying this property to the state
|(x + C
2
)
∗
X
in Eq. (24.39), namely, for each of the terms
|
x + y
in the sum, we

24.3 Calderbank–Shor–Steine (CSS) codes 513
obtain:
H
⊗n
|(x + C
2
)
∗
X
≡
1
√
|
C
2
|
2
n
z
y∈C
2
(
−1
)
(
x+y
)
·(z+e
Y
)
|
z
. (24.41)
By introducing z
= z + e
Y
, we may rewrite the above in the form
H
⊗n
|(x + C
2
)
∗
X
≡
1
√
|
C
2
|
2
n
z
y∈C
2
(
−1
)
(
x+y
)
·z
|z
+ e
Y
. (24.42)
To reduce the right-hand side in Eq. (24.42) to a single summation, we first isolate the
term involving the dot-product y · z
as follows
H
⊗n
|(x + C
2
)
∗
X
≡
1
√
|
C
2
|
2
n
z
y∈C
2
(
−1
)
y·z
(
−1
)
x·z
|z
+ e
Y
. (24.43)
It can be shown through a (not so trivial but tractable) exercise that the sum in brackets
[
·
]
is equal to |C
2
|for all z
∈ C
⊥
2
(C
⊥
2
being the dual of the C
2
code), and zero otherwise
(z
/∈ C
⊥
2
). Hence, the simplification of the definition in Eq. (24.43):
H
⊗n
|(x + C
2
)
∗
X
≡
5
|
C
2
|
2
n
z
∈C
⊥
2
(
−1
)
x·z
|z
+ e
Y
. (24.44)
Except for the normalization factor and the phase terms, the above expression is similar
to that in Eq. (24.38) concerning the bit-flip errored state, but here with e
Y
as the error
pattern and C
⊥
2
as the code (as opposed to e
X
and C
2
, respectively). A similar error-
correction procedure can, thus, be implemented. First, we append an n-qubit ancilla |0
to this state, transforming each term in the sum in Eq. (24.44)into|z
+ e
Y
|0, then
pass the result through a quantum circuit to achieve the transformation
|z
+ e
Y
|0→|z
+ e
Y
|
˜
H
⊥
(z
+ e
Y
)=|z
+ e
Y
|
˜
H
⊥
z
+
˜
H
⊥
e
Y
)
≡|z
+ e
Y
|
˜
H
⊥
e
Y
),
(24.45)
where
˜
H
⊥
is the parity-check matrix of the code C
⊥
2
,forwhich
˜
H
⊥
z
= 0. Measuring
each qubit in the ancilla |
˜
H
⊥
e
Y
yields the syndrome vector
˜
H
⊥
e
Y
and, hence, the full
error diagnosis e
Y
, which is common to each of the series terms in Eq. (24.44). The
ancilla can then be discarded and each of the errored qubits can be corrected (or back
flipped) by applying Y gates in the corresponding circuit wires, to obtain the Y -corrected
state
H
⊗n
|(x + C
2
)
∗
XY
≡
5
|
C
2
|
2
n
z
∈C
⊥
2
(
−1
)
x·z
|z
. (24.46)
The final step consists of passing each qubit in the above state through a Hadamard gate,
i.e., to obtain the state H
⊗n
H
⊗n
|(x + C
2
)
∗
XY
. Here, there is no point in going through
the detailed calculation of such an operation, because as a useful property, H and H
⊗n
are self-inverse operators (HH = I, H
⊗n
H
⊗n
= I
⊗n
). If we let e
Y
= 0inEq.(24.44),

514 Quantum error correction
we obtain
H
⊗n
|(x + C
2
)
∗
X
≡
5
|
C
2
|
2
n
z
∈C
⊥
2
(
−1
)
x·z
|z
≡ H
⊗n
|x + C
2
,
(24.47)
which is precisely the same state as H
⊗n
|(x + C
2
)
∗
XY
, and also the H
⊗n
transform of
the error-free state |x +C
2
! Thus, a second application of H
⊗n
on the states defined in
either Eq. (24.46)orEq.(24.47) yields
H
⊗n
H
⊗n
|(x + C
2
)
∗
XY
= H
⊗n
H
⊗n
|(x + C
2
)
∗
X
=|x + C
2
≡
1
√
|
C
2
|
y∈C
2
|
x + y
,
(24.48)
which yields our initial CSS-encoded state |x + C
2
. Thus, the second round of correc-
tion concerning Z -errors has successfully restored the CSS codeword in its full integrity.
The next section concerning the Steane code provides an applied illustration of the
CSS(C
1
, C
2
) codes.
24.4 Hadamard–Steane code
The Hadamard–Steane code, also sometimes called the Steane code, belongs to the
CSS(C
1
, C
2
) family. It has the same bit-flip and phase-flip error correction capability
as the earlier-described Shor code, namely, up to one error in either or both cases, but
it uses 7-qubit codewords as opposed to nine qubits in the second case. It is based on
the Hamming code C
1
= C = (7, 4), which was described in Chapter 11, and its dual
C
2
= C
⊥
. To recall, a possible parity-check matrix
˜
H for the (7, 4) Hamming code,
which we used in that chapter,
4
is defined as:
˜
H =
1101100
1011010
0111001
. (24.49)
4
Some other possible parity-check matrices
˜
H for the (7, 4) Hamming code commonly used in the literature
or the Internet are
˜
H =
1001011
0101101
0010111
,
˜
H =
1101001
0101110
1110000
,
˜
H =
0001111
0110011
1010101
.

24.4 Hadamard–Steane code 515
Table 24.4 Block codewords Y of the
Hamming code C
1
= (7, 4),aspro-
duced from the generator matrix
˜
G =
˜
H
T
,
according to Y = X
˜
G. The parity bits are
showninbold.
Message word X Block code Y
0000 0000 000
0001 0001 111
0010 0010 011
0011 0011 100
0100 0100 101
0101 0101 010
0110 0110 110
0111 0111 001
1000 1000 110
1001 1001 001
1010 1010 101
1011 1011 010
1100 1100 011
1101 1101 100
1110 1110 000
1111 1111 111
In the convention of left matrix-vector multiplication, the corresponding generator matrix
˜
G is:
5
˜
G =
1000110
0100101
0010011
0001111
. (24.50)
Note that the above definitions correspond to a code expressed in a systematic form,as
shown by the fact that the right 3 × 3 sub-matrix of
˜
H and the left 4 × 4 sub-matrix of
˜
G are identity matrices. The |C
1
|=2
k
= 2
4
= 16 block codewords Y = X
˜
G of C
1
=
(7, 4), which were already listed in Chapter 11, are reproduced here for convenience in
Table 24.4.
Consider next the dual code C
2
= C
⊥
. By definition, its parity-check matrix is
ˆ
H =
˜
G
T
, with corresponding generator matrix
ˆ
G =
˜
H
T
. From the definitions in Eqs. (24.49)
5
In Chapter 11 we used the convention of left vector-matrix multiplication. Thus, the codewords are generated
according to the product Y = X
˜
G,seeEq.(11.2)inChapter 11. Under this convention, for an (n, k) code
with m = n − k, the systematic form of the generator and parity-check matrices are
˜
G = [I
k
|P
k×m
]and
˜
H = [(P
T
)
m×k
|I
m
], respectively. Thus, for the (7, 4) Hamming code (m = 3),
˜
G is a 4 × 7 matrix and
˜
H
is a 3 ×7 matrix.

516 Quantum error correction
Table 24.5 Block codewords Y of the dual
code C
2
= C
⊥
1
= (7, 3) of the Hamming
code C
1
= (7, 4), as produced from the gen-
erator matrix
ˆ
G =
˜
H
T
, where
˜
H is the parity-
check matrix of C
1
, according to Y =
ˆ
GX.
The parity bits are shown in bold.
Message word X Block code Y
000 0000 000
001 0111 001
010 1011 010
011 1100 011
100 1101 100
101 1010 101
110 0110 110
111 0001 111
and (24.50), we obtain:
ˆ
H =
˜
G
T
=
1000
0100
0010
0001
1101
1011
0111
, (24.51)
ˆ
G =
˜
H
T
=
110
101
011
111
100
010
001
. (24.52)
As defined in Eq. (24.52), the 7 ×3 generator matrix
ˆ
G of the dual code C
2
generates
seven-bit codewords from three-bit message words, this time using the right vector-
matrix multiplication, i.e., Y =
ˆ
GX. Since
ˆ
G has the systematic form
ˆ
G = [P
4×3
|I
3
],
and since
ˆ
G
ˆ
H
T
=
˜
H
T
˜
G = 0 =
˜
G
˜
H
T
=
ˆ
H
T
ˆ
G, the dual code is a valid (n, k) = (7, 3)
code (note that it is not a Hamming code since n = 2
n−k
− 1). The |C
2
|=2
k
= 2
3
= 8
block codewords Y =
ˆ
GX are listed in Table 24.5.
Analyzing Table 24.5, we first note that, as expected, the code C
2
is in systematic form,
with the four parity bits appearing at the left of the codewords Y and the three message
bits (X) appearing at the right. Next, it is easily checked that the bit-wise sum ⊕ of any
two codewords in C
2
belongs to C
2
; since C
2
contains the identity element 0000000,
(C
2
, ⊕)isagroup. Then, we observe that the minimum Hamming distance (the minimum
difference in bit positions between any two codewords) is d
min
= 3. This indicates that
