Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


23.3 Capacity of some quantum channels 487
the following property is always satisfied:
S + S
E
(ρ,ε) ≥ 0. (23.49)
This last result shows that the entropy change caused by the quantum operation ε on
both the quantum channel and the “outside world” is always nonnegative, which recalls
the second law of thermodynamics, according to which the entropy of a closed system
may only increase on any physical transformation or evolution from its initial state.
23.3 Capacity of some quantum channels
In this section, I apply the HSW theorem to evaluate the capacity of different types of
quantum channel. We assume that the originator source has, for symbols, the pure states
ρ
i
=|ψ
i
ψ
i
|which are associated within a quantum message (or codeword) with some
probability distribution p
i
. For convenience, we introduce
χ
= S
&
ε
3
i
p
i
ρ
i
4'
−
i
p
i
S
[
ε
(
ρ
i
)
]
, (23.50)
to which, after the HSW theorem, the channel capacity χ = max(χ
) corresponds.
Before touching upon any examples, it is interesting to consider the case of ideal,
constant or “noiseless” channels. This is the case where ε
(
ρ
i
)
= ρ
i
and, hence, from
Eq. (23.50):
χ
ideal
=
3
i
p
i
ρ
i
4
−
i
p
i
S
(
ρ
i
)
≡ S
3
i
p
i
ρ
i
4
, (23.51)
where we used the property that for any pure state ρ
i
the VN entropy S(ρ
i
) is zero. The
result in Eq. (23.49) shows that in this ideal case, χ
actually represents the VN entropy
of the originator’s message source S(ρ) = S(ρ
i
). The “ideal channel” capacity is given
by χ
ideal
= max(χ
ideal
), or
χ
ideal
= max(χ
ideal
) = max
p
i
&
S
3
i
p
i
ρ
i
4'
≡ max S(ρ). (23.52)
This maximization problem, thus, addresses the question of how much classical infor-
mation can be conveyed through any given message ρ before transmission through any
quantum channel. Intuitively, we expect that for nonideal channels we have the property
χ ≤ χ
ideal
, (23.53)
meaning that, obviously, noisy transmission does not improve the information of the
message source. This is just like in the classical case, with the mutual information satis-
fying H (X; Y ) ≤ H (X), and with the capacity C = max[H (X; Y )] ≤ max[H (X)] = 1
bit. The following examples will illustrate the fact that the quantum channel capacity
χ cannot, indeed, exceed the highest-possible VN entropy of the originator source, i.e.,
χ
ideal
= max[S(ρ)].
488 Quantum channel noise and channel capacity
Example 23.1: Depolarizing channel
In Eq. (23.8) we have seen that this channel is defined by the operation
ε(ρ
i
) = p
I
2
+ (1 − p)ρ
i
. (23.54)
Assuming the orthogonal symbols ρ
1
=|00| and ρ
2
=|11|, we obtain
ε
3
i
p
i
ρ
i
4
= ε
[
p
1
ρ
1
+ (1 − p
1
)ρ
2
]
= p
I
2
+ (1 − p)
[
p
1
ρ
1
+ (1 − p
1
)ρ
2
]
=
p
2
10
01
+ (1 − p)p
1
10
00
+ (1 − p)(1 − p
1
)
00
01
=
p
2
10
01
+ (1 − p)
p
1
0
01− p
1
≡
p
2
+ (1 − p)p
1
0
0
p
2
+ (1 − p)(1 − p
1
)
, (23.55)
and the corresponding VN entropy
S
&
ε
3
i
p
i
ρ
i
4'
=−
p + 2(1 − p)p
1
2
log
p + 2(1 − p)p
1
2
+
p + 2(1 − p)(1 − p
1
)
2
log
p + 2(1 − p)(1 − p
1
)
2
.
(23.56)
As we have seen in the previous section, the VN entropy of the recipient symbols is
S[ε(ρ
1
)] = S[ε(ρ
2
)] = f ( p/2), hence,
i
p
i
S
[
ε(ρ
i
)
]
= p
1
f
#
p
2
$
+ (1 − p
1
) f
#
p
2
$
≡ f
#
p
2
$
. (23.57)
From Eq. (23.50), we finally obtain
χ
(p, p
1
) = S
&
ε
3
i
p
i
ρ
i
4'
−
i
p
i
S
[
ε(ρ
i
)
]
=−
p
2
+ (1 − p)p
1
log
p
2
+ (1 − p)p
1
+
p
2
+ (1 − p)(1 − p
1
)
log
p
2
+ (1 − p)(1 − p
1
)
− f
#
p
2
$
.
(23.58)
In the above equation, it is clear that the first term in braces, corresponding to the
definition in Eq. (23.56), is maximized if we choose the two symbols to have equal
probabilities p
1
= 1 − p
2
= 1/2, which gives
S
&
ε
3
i
p
i
ρ
i
4'
=−
1
2
log
1
2
+
1
2
log
1
2
= f
1
2
= 1. (23.59)
23.3 Capacity of some quantum channels 489
0
0.2
0.4
0.6
0.8
1
0 0.2 0.4 0.6 0.8 1
Probability
p
Quantum channel capacity χ
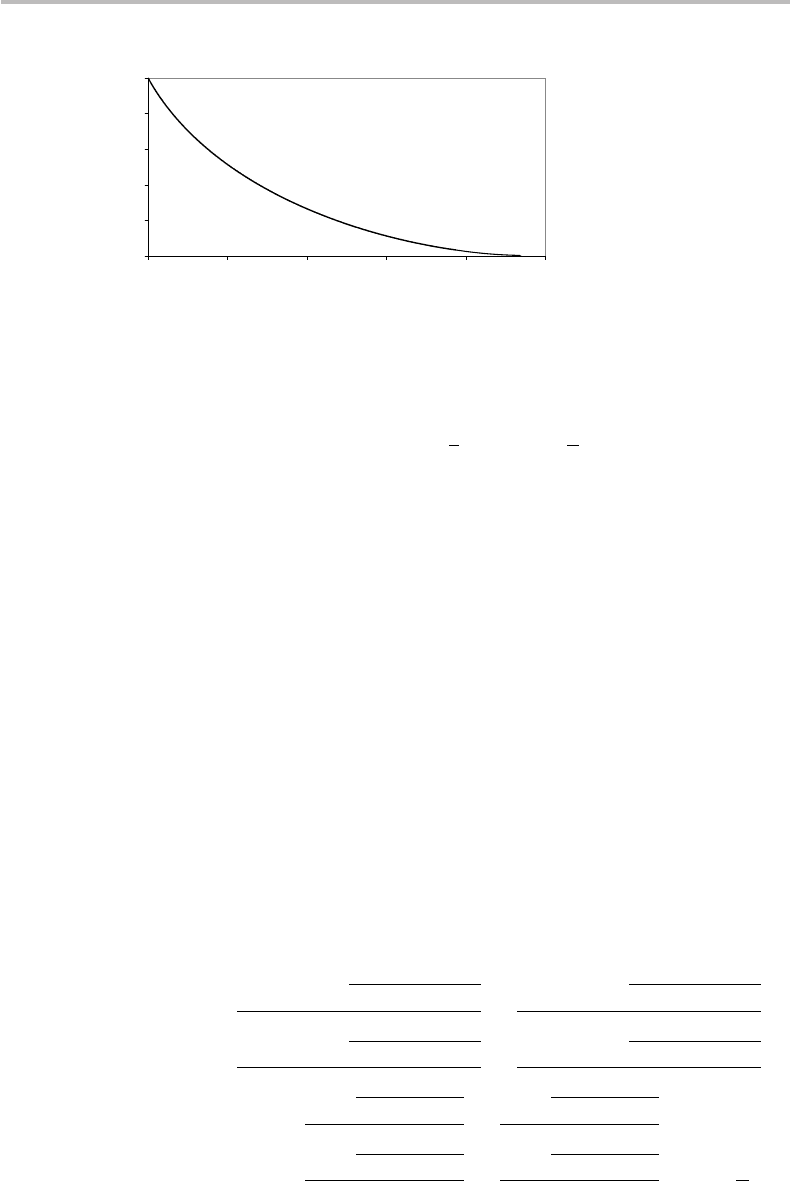
Figure 23.1 Quantum capacity χ( p) of the depolarizing channel as a function of the depolarizing
parameter p.
Thus, we obtain the channel capacity χ :
χ(p) = max χ
p,
1
2
≡ 1 − f
#
p
2
$
. (23.60)
As expected from the analysis in the previous section, the capacity vanishes for p = 1,
which corresponds to a “useless channel,” projecting any random symbol ρ
i
onto
σ = ε(ρ
i
) = I /2 as shown from Eq. (23.54). The highest capacity χ (0) = 1 bit is
obtained for p = 0, in which case the quantum channel ε is constant or “ideal,” or
“noiseless,” i.e., σ = ε(ρ
i
) = ρ
i
, but this case is of no interest here. Figure 23.1 shows
a plot of the depolarizing channel capacity as a function of the depolarizing proba-
bility parameter p. It is seen from the figure that, as expected, the channel capacity
monotonously decays as the depolarizing parameter increases from p = 0top = 1. To
provide a practical engineering interpretation of the above result, assume, for instance,
that p = 0.1, which yields f (p/2) ≈ 0.25 (see Fig. 4.7), and, thus, defines a channel
capacity of χ = 0.75 bit. The HSW theorem states that it is possible to transmit code-
words of sufficient lengths with arbitrary error probability provided the code rate satisfies
R <χ = 0.75. Given a block code (n, k), the code rate must satisfy R = k/n < 0.75,
which means that the code must include 25% redundancy bits and 75% payload
bits.
The exercises provide other application examples of the depolarizing channel capac-
ity. Here, it is worth showing the results obtained when assuming the codeword sym-
bols |0, |+ instead of |0, |1. It is a tedious but tractable exercise to show that the
corresponding capacity takes the form:
χ(p) = max
p
1
−
1 + (1 − p)
1 − 2 p
1
(1 − p
1
)
2
log
1 + (1 − p)
1 − 2 p
1
(1 − p
1
)
2
−
1 − (1 − p)
1 − 2 p
1
(1 − p
1
)
2
log
1 − (1 − p)
1 − 2 p
1
(1 − p
1
)
2
+(1 − p
1
)
1 +
1 − p(2 − p)
2
log
1 +
1 − p(2 − p)
2
+(1 − p
1
)
1 −
1 − p(2 − p)
2
log
1 −
1 − p(2 − p)
2
− p
1
f
#
p
2
$
.
(23.61)
490 Quantum channel noise and channel capacity
0
0,2
0,4
0,6
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
0
0,2
0,4
0,6
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
0
0,2
0,4
0,6
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
0
0,2
0,4
0,6
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
0
0,2
0,4
0,6
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
0
0,2
0,4
0,6
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
0
0,2
0,4
0,6
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
0
0.2
0.4
0.6
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Depolarizing parameter
p
=
1
p
0.5
0.4
0.3
0.2
0.1
0.05
0.025
0.01
)
,(
´
max
1
1
pp
p
χ
χ
=
0.6
0.7
0.8
0.9
0.95
0.975
0.99
χ
´
(
p,p
1
)
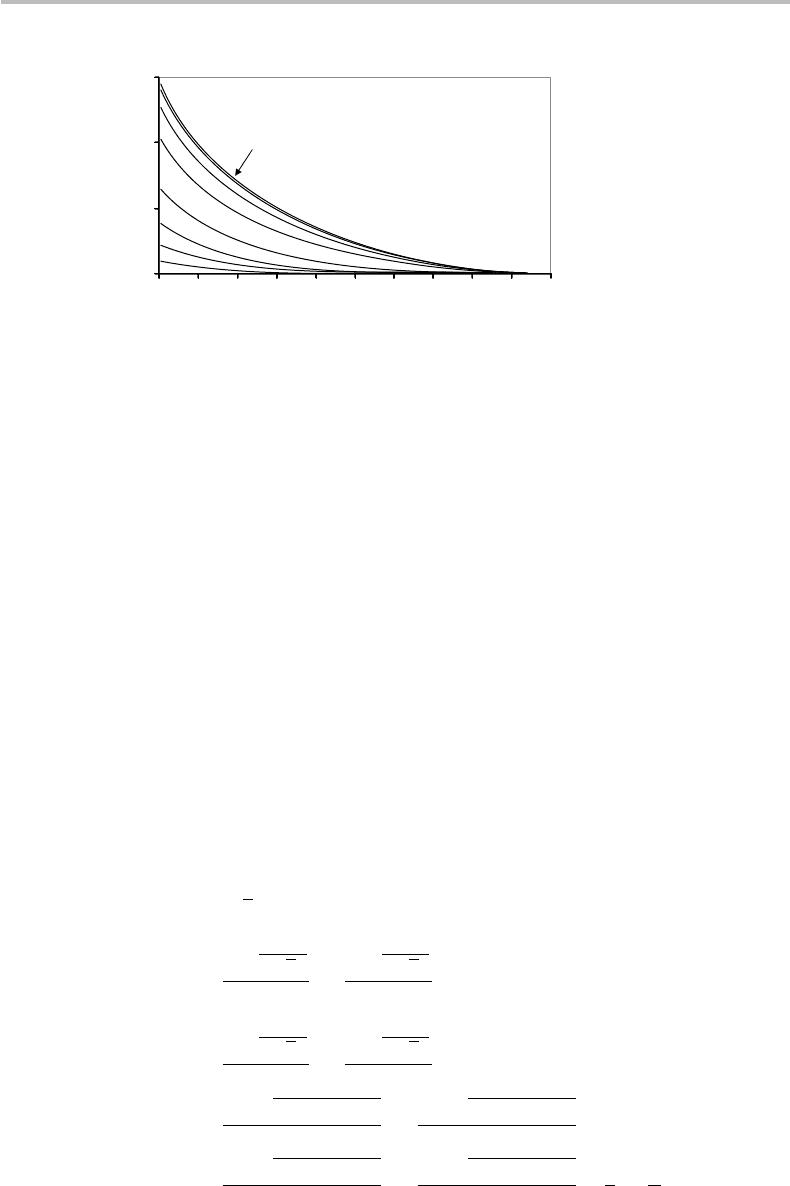
Figure 23.2 Plots of χ
(p, p
1
) as a function of the depolarizing parameter p in
depolarizing-channel, and corresponding channel capacity χ( p) = max χ
(p, p
1
) (codewords
formed by pure states |0, |+ with probabilities p
1,
1 − p
1
, respectively).
The expression in brackets {χ
(p, p
1
)} in Eq. (23.61) can be maximized by numer-
ically solving the transcendental equation ∂χ
(p, p
1
)/∂p
1
= 0. But we may as well
directly infer the answer, as it will be shown further on. First, we may just plot
the function χ
(p, p
1
) for different values of the parameter p
1
(probability associ-
ated with |0), as illustrated in Fig. 23.2. From the figure, we first note the property
χ
(p, p
1
) = χ
(p, 1 − p
1
). Second, we observe that in all cases, the functionχ
(p, p
1
)
is maximal at p = 0 (constant or noiseless channel) and zero at p = 1 (useless chan-
nel). Third, we see that the channel capacity χ ( p) = max χ
(p, p
1
) is achieved for
p
1
= 0.5. This was expected, since this condition corresponds to maximum uncer-
tainty in the occurrence of the |0, |+ qubits forming the codewords. From the
property in Eq. (23.53), the constant or noiseless capacity, χ(0), must correspond
to the (maximum possible) VN entropy of originator’s source, max[S(ρ)] = χ
ideal
,
as discussed earlier and also formally established in the exercise. Substituting
p
1
= 0.5intoEq.(23.61), we obtain the following analytical form of the channel
capacity:
χ ≡ χ
p,
1
2
=
−
1 +
1 − p
√
2
2
log
1 +
1 − p
√
2
2
−
1 −
1 − p
√
2
2
log
1 −
1 − p
√
2
2
+
1 +
1 − p(2 − p)
4
log
1 +
1 − p(2 − p)
2
+
1 −
1 − p(2 − p)
4
log
1 −
1 − p(2 − p)
2
−
1
2
f
#
p
2
$
.
(23.62)

23.3 Capacity of some quantum channels 491
Substituting p = 0 in the above, we get the upper bound for the channel capacity, which
corresponds to the originator’s maximum source entropy max[S(ρ)]:
χ
ideal
= max S(ρ)
= χ
0,
1
2
≡−
2 +
√
2
4
log
2 +
√
2
4
+
2 −
√
2
4
log
2 −
√
2
4
B
.
(23.63)
This example, thus, provides an illustration of the HSW maximization problem, leading,
in this case, to a tractable analytical solution. It also illustrates the property χ(p) ≤
χ
ideal
= max S(ρ), which can be used to guide the maximization problem solving.
Example 23.2: Bit-flip channel
The quantum operation of this channel is defined in Eq. (23.13). Assuming the orthogonal
symbols ρ
1
=|00| and ρ
2
=|11|, we obtain
ε
3
i
p
i
ρ
i
4
= ε
[
p
1
ρ
1
+ (1 − p
1
)ρ
2
]
= pX
[
p
1
ρ
1
+ (1 − p
1
)ρ
2
]
X + (1 − p)
[
p
1
ρ
1
+ (1 − p
1
)ρ
2
]
= pp
1
Xρ
1
X + p(1 − p
1
)Xρ
2
X + (1 − p) p
1
ρ
1
+ (1 − p)(1 − p
1
)ρ
2
=
pp
1
01
10
10
00
01
10
+ p(1 − p
1
)
01
10
00
01
01
10
+ (1 − p)p
1
10
00
+ (1 − p)(1 − p
1
)
00
01
= pp
1
00
01
+ p(1 − p
1
)
10
00
+
(1 − p)p
1
0
00
+
00
0(1− p)(1 − p
1
)
≡
p + p
1
− 2 pp
1
0
01−
[
p + p
1
− 2 pp
1
]
. (23.64)
and the corresponding VN entropy
A = S
&
ε
3
i
p
i
ρ
i
4'
=−
(
p + p
1
− 2 pp
1
)
log
(
p + p
1
− 2 pp
1
)
+
[
1 −
(
p + p
1
− 2 pp
1
)
]
log
[
1 −
(
p + p
1
− 2 pp
1
)
]
B
≡ f
(
p + p
1
− 2 pp
1
)
.
(23.65)

492 Quantum channel noise and channel capacity
Next, we calculate the quantum operation ε onto ρ
1
and ρ
2
along with the corresponding
entropies:
ε(ρ
1
) = pXρ
1
X + (1 − p)ρ
1
≡ p
00
01
+ (1 − p)
10
00
≡
1 − p 0
0 p
→
S
[
ε(ρ
1
)
]
=−[(1 − p)log(1− p) + p log p]
≡ f (1 − p)
≡ f ( p)
, (23.66)
ε(ρ
2
) = pXρ
2
X + (1 − p)ρ2
≡ p
10
00
+ (1 − p)
00
01
≡
p 0
01− p
→
S
[
ε(ρ
2
)
]
≡ f ( p).
(23.67)
Hence, we obtain
B =
i
p
i
S
[
ε
(
ρ
i
)
]
= p
1
f ( p) +(1 − p
1
) f (p)
≡ f
(
p
)
.
(23.68)
Combining the results in Eqs. (23.65) and (23.68), we finally obtain the channel capacity
χ(p, p
1
) = max
p
1
(χ
)
≡ max
p
1
(
A − B
)
≡ max
p
1
[ f (p + p
1
− 2 pp
1
) − f ( p)].
(23.69)
We note that the argument satisfies the property χ
(p, p
1
) = χ
(p, 1 − p
1
). The max-
imization problem can be solved analytically by studying the partial derivatives
∂χ
(p, p
1
)/∂p
1
and ∂
2
χ
(p, p
1
)/∂p
2
1
, but we may observe, again, that the capacity
cannot exceed the amount χ
ideal
= max S(ρ). Using the definition of the symbol density
operator ρ = p
1
ρ
1
+ (1 − p
1
)ρ
2
, we clearly have S(ρ) = f ( p
1
), and χ
ideal
= max S(ρ),
yielding p
1
= 1/2, as expected (maximum VN entropy is obtained for a uniform
message-symbol distribution). Thus, we have for all p the channel capacity:
χ(p) = χ
p,
1
2
=
[
f
(
p + 1/2 − 2 p/2
)
− f
(
p
)
]
≡ 1 − f
(
p
)
.
(23.70)
23.4 Exercises 493
0
0,2
0,4
0,6
0,8
1
0
0,2
0,4
0,6
0,8
1
0
0,2
0,4
0,6
0,8
1
0
0,2
0,4
0,6
0,8
1
0
0,2
0,4
0,6
0,8
1
0
0,2
0,4
0,6
0,8
1
0 0.2 0.4 0.6 0.8 1
0
0,2
0,4
0,6
0,8
1
=
1
p
0.5
0.4
0.3
0.2
0.1
0.05
0.01
0.6
0.7
0.8
0.9
0.95
0.99
χ
(
p,p
1
)
),(
´
max
1
1
pp
p
χ
χ
=
0
1
Bit-flip parameter
p
´
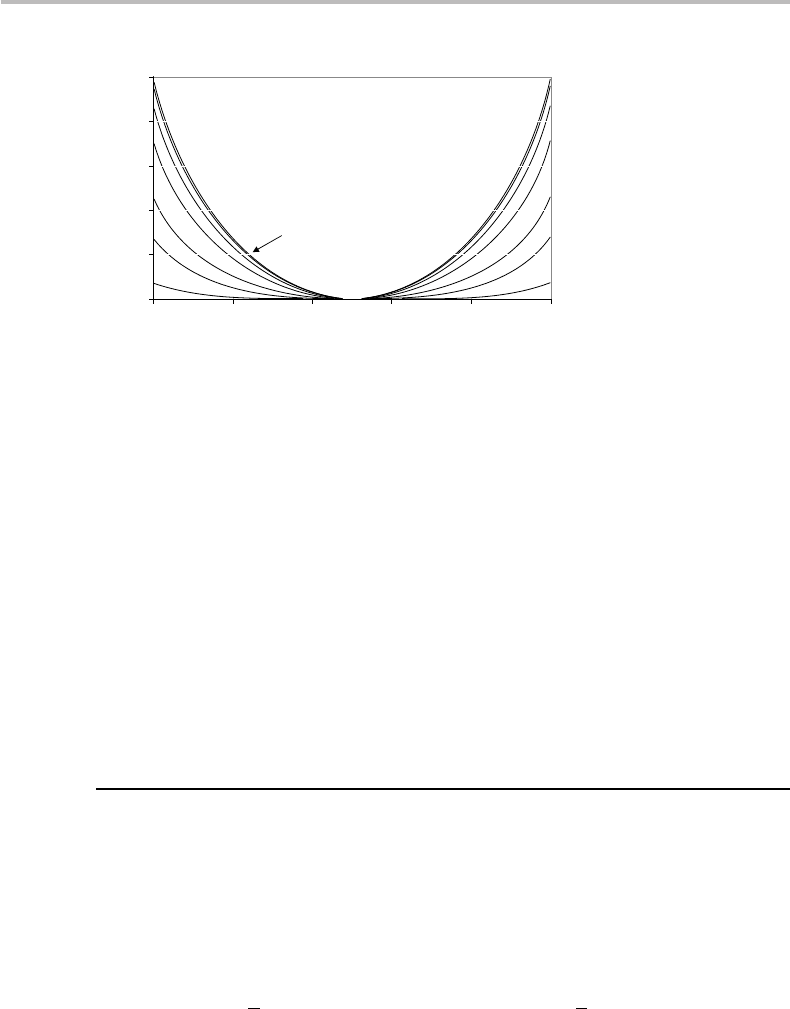
Figure 23.3 Plots of χ
(p, p
1
) as a function of the bit-flipping parameter p in the bit-flip channel,
and corresponding channel capacity χ( p) = max χ
(p, p
1
) (codewords formed by pure states
|0, |+ with probabilities p
1
, 1 − p
1
, respectively).
Figure 23.3 shows plots of χ
(p, p
1
)for p
1
= 0to p
1
= 1 through different incre-
ments (recalling that χ
(p, p
1
) = χ
(p, 1 − p
1
)), with the top curve χ( p) = χ
(p, 1/2)
representing the channel capacity. Interestingly, the channel capacity is seen to have
two maxima, i.e., for p = 0 and p = 1. These two limiting cases correspond to the
noiseless channel, and the “deterministic” bit-flip channel, respectively. A determin-
istic bit-flipping is simply a change of code polarity, meaning that the classical cbit
codewords from originator to recipient are exactly inverted or complemented, which
entails no information degradation or error. The other limiting situation is obtained for
p = 1/2, meaning that the qubit has a 50% chance of being flipped and a 50% chance of
being conserved in its integrity. The recipient’s measurement amounts to a coin-flipping
experiment, and all initial information is lost, which is the situation of the useless
channel.
23.4 Exercises
23.1 (B): Given the Pauli matrices X, Y, Z (see definition in Chapter 16), show that for
any 2 × 2 operator A with unity trace, and for q = 3 p/4, the following relation
holds:
q
3
(XAX + YAY + ZAZ) +(1 −q)A = p
I
2
+ (1 − p)A.
23.2 (M): Analyze the effect of the bit-flip quantum channel defined by
σ = ε(ρ) = pXρ X + (1 − p)ρ,
with p being a probability distribution and X the Pauli matrix
X =
01
10
,

494 Quantum channel noise and channel capacity
in the case where the density operator ρ is nondiagonal. Determine the entropy
change S = S(σ ) − S(ρ) in the case ρ =|00| and ρ =|11|.
23.3 (M): Analyze the effect of the phase-flip quantum channel as defined by
σ = ε(ρ) = pZρ Z +
(
1 − p
)
ρ,
with p being a probability distribution and Z the Pauli matrix
Z =
10
0 −1
,
in the case where the density operator ρ is nondiagonal. Determine the entropy
change S = S(σ ) − S(ρ) in the four cases ρ =|00|, ρ =|11|, ρ = |++|
and ρ = |−−|.
23.4 (M): Analyze the effect of the bit-phase-flip quantum channel as defined by
σ = ε(ρ) = pYρY + (1 − p)ρ,
with p being a probability distribution and Y the Pauli matrix
Y =
0 −i
i0
,
in the case where the density operator ρ is nondiagonal. Determine the entropy
change S = S(σ ) − S(ρ) in the four cases ρ =|00|, ρ =|11|, ρ = |++|,
and ρ = |−−|.
23.5 (M): Determine the quantum channel capacity corresponding to the depolarizing
channel
ε(ρ
i
) = p
I
3
+ (1 − p)ρ
i
,
assuming the three-symbol alphabet
ρ
1
=|00|,ρ
2
=|11|,ρ
3
=|22|
associated with probabilities p
1
, p
2
, p
3
. Provide a plot of the capacity as a function
of the depolarizing parameter p.
23.6 (T): Determine the quantum channel capacity corresponding to the depolarizing
channel
ε(ρ) = pZρ Z + (1 − p)ρ,
assuming the two-symbol alphabet
ρ
1
=|00|,ρ
2
=|+
+
|
=
|0+|1
√
2
associated with probabilities p
1
, p
2
.

23.4 Exercises 495
Hint:plot
χ
(p) = S(ε) −S(ε)
as a function of p, for different values of p
1
and justify that the capacity χ =
max(χ
) is achieved for p
1
= p
2
= 1/2; also show that χ(p) ≤ χ(0) = S(ρ),
where χ(0) is the capacity of the constant or noiseless quantum channel and S(ρ)
is the VN entropy of the originator source.

24 Quantum error correction
This chapter deals with the subject of quantum error correction and the related codes
(QECC), which can be applied to noisy quantum channels and quantum memories with
the purpose of preserving or protecting the information integrity. I first describe the
basics of quantum repetition codes, as applicable to bit-flip and phase-flip quantum
channels. Then I consider the 9-qubit Shor code, which has the capability of diagnosing
and correcting any combination of bit-flip and phase-flip errors, up to one error of each
type. Furthermore, it is shown that the Shor code is, in fact, capable of fully restoring
qubit integrity under a continuum of bit or phase errors, a property that has no counterpart
in the classical world of error-correction codes. But the exploration of QECC does not
stop here! We shall discover the elegant Calderbank–Shor–Steane (CSS) codes, which
have the capability of correcting any number of errors t, both bit-flip and phase-flip.
As an application of the CSS code, I then describe the 7-qubit Hadamard–Steane code,
which can correct up to one error on single qubits. A corresponding quantum circuit,
based on an original generator-matrix example, is presented.
24.1 Quantum repetition code
In Chapter 11, we saw that the simplest form of error-correction code (ECC) is the
repetition code, based on the principle of majority logic. The background assumption is
that in a given message sequence, or bit string, the probability of a bit error is sufficiently
small for the majority of bits to be correctly transmitted through the channel. It then
suffices to repeat each of the bits a certain number of times, at the cost of wasting
the channel resource or “bandwidth.” For instance, if one repeats each of the bits four
times, the original bit sequence 0111 is encoded into (underscores introduced for reading
clarity):
0000
1111 1111 1111,
which may yield at the channel output
0010
1111 0111 1011.
Clearly, a single bit error occurred in the first and last two blocks of the transmitted
message, and the simple rule of majority logic suffices to detect such errors and revert
the bits to the correct values. If p is the probability of error for a single bit, the probability
