Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


22.2 Schumacher’s quantum coding theorem 467
demonstrating such a statement. Suffice it to take for granted as a postulate that, given ε,
it is possible to make p() arbitrarily close to unity (with δ chosen sufficiently small),
if the message length n is sufficiently large. Consistently, the dimension of the typical
subspace, dim() = tr(E), also increases. But can we show to what extent?
To answer the above question, I shall now introduce a key theorem concerning the
dimension of the typical subspace. Given a message length n, the VN entropy S(ρ)of
the quantum-symbol source, the two parameters ε, δ, then the dimension dim()ofthe
corresponding typical subspace is bounded according to:
(1 − δ)2
n(S−ε)
≤ dim() ≤ 2
n(S+ε)
. (22.28)
The proof for this is actually straightforward. First, we sum each term in the double
inequality in Eq. (22.24) from i = 1toi = dim() to obtain
dim()
i=1
2
−n(S+ε)
≤
dim()
i=1
µ
i
≤
dim()
i=1
2
−n(S−ε)
↔
dim()2
−n(S+ε)
≤ p() ≤ dim()2
−n(S−ε)
.
(22.29)
Second, we substitute the two properties 1 −δ ≤ p() and p() ≤ 1 into Eq. (22.29)
and then obtain
dim()2
−n(S+ε)
≤ p() ≤ 1
1 − δ ≤ p() ≤ dim()2
−n(S−ε)
↔
dim() ≤ 2
n(S+ε)
dim() ≥ (1 − δ)2
n(S−ε)
↔
(1 − δ)2
n(S−ε)
≤ dim() ≤ 2
n(S+ε)
,
(22.30)
which is in Eq. (22.28) and, thus, proves the typical subspace theorem.
Our exploitation of the above theorem will be made purposefully simple, the goal
being to convey only an intuitive proof of Schumacher’s quantum coding theorem (usually
called Schumacher’s noiseless channel coding theorem) and, thus, avoid lengthier and
more academically involved developments.
Define the parameter R such that R = S + ε, with the condition R ≤ 1(or0<ε≤
1 − S). From the typical subspace theorem, the dimension of the typical subspace
satisfies dim() ≤ 2
nR
. Thus, we may use up to 2
nR
, ε-typical codewords, such that
for any δ>0 the condition p() ≥ 1 −δ is satisfied for message lengths n sufficiently
large. In this case, we may say that the compression scheme is “reliable,” i.e., corresponds
to arbitrary high fidelity. Under these conditions, Schumacher’s quantum coding theorem
states that there exists a reliable compression code, with arbitrarily high transmission
fidelity, and compression factor η = R. We note that R is strictly higher than the VN
entropy S, which sets an ultimate limit to the achievable compression factor (R > S).
The second part of the theorem is that any compression code with R < S is not reliable.
Here, again to avoid lengthy mathematical developments, I shall only concentrate on the
reliable compression code, and provide a simple description.

468 Quantum data compression
The quantum symbols forming the message are now assumed to be the eigenstates
|λ
i
of the density operator ρ, and the possible messages are the eigenstates |µ
i
of
the operator ρ
M
= ρ
⊗n
. The originator then proceeds to encode these into states of the
form
|µ
i
=U|µ
i
=|µ
comp1
⊗|0
rest
, (22.31)
where |µ
comp1
is a compressed state of nR < n qubits, and |0
rest
=|00 ...0=|0
⊗q
represents the remainder of the block, of length q = n(1 − R) qubits. The originator
then makes “fuzzy” measurements on each of the qubits from the remainder state. If
theoutcomeis00...0, then|µ
i
has been projected onto the typical subspace , and
|µ
comp1
is sent through the quantum channel. If the outcome is anything different,
the originator sends an nR qubit message |ψ
comp2
, as a “junk” substitute, which is
determined by the same rotation U such that U
−1
(|ψ
comp2
⊗|0
rest
) =|µ
junk
∈.As
in the previous (n = 3) example, the recipient just needs to append |0
rest
to the received
message, followed by the inverse transformation U
−1
on this n-qubit state. If E is the
projector onto the typical subspace , and |µ
i
the original message that has been sent,
the corresponding density operator ˜ρ
i
of the received/uncompressed message takes a
form similar to that in Eq. (22.19):
˜ρ
i
= E|µ
i
µ
i
|E +µ
i
|(I − E)|µ
i
|µ
junk
µ
junk
|
= E|µ
i
µ
i
|E + ˜ρ
junk
.
(22.32)
The fidelity of the transmission must be averaged over all the message possibilities, each
with probability µ
i
, as follows:
˜
F =
2
n
i=1
µ
i
µ
i
|˜ρ
i
|µ
i
, (22.33)
which, by substituting the result in Eq. (22.32), yields
˜
F =
2
n
i=1
µ
i
µ
i
|(E|µ
i
µ
i
|E)|µ
i
+
2
n
i=1
µ
i
µ
i
|˜ρ
junk
|µ
i
=
2
n
i=1
µ
i
(µ
i
|E|µ
i
)
2
+ tr(˜ρ
junk
)
≥
2
n
i=1
µ
i
(µ
i
|E|µ
i
)
2
.
(22.34)
The last inequality is caused because the junk contribution is nonnegative; i.e.,
tr( ˜ρ
junk
) ≥ 0. Then we use the property that for any real x we have x
2
≥ 2x − 1
because
(
x − 1
)
2
≥ 0. Thus, each term x
2
=
(
µ
i
|E|µ
i
)
2
in the above right-hand side

22.3 A graphical and numerical illustration 469
summation is greater than or equal to 2x − 1 = 2µ
i
|E|µ
i
−1, which yields
˜
F ≥
2
n
i=1
µ
i
(
2µ
i
|E|µ
i
−1
)
= 2
2
n
i=1
µ
i
|µ
i
E|µ
i
−
2
n
i=1
µ
i
≡ 2tr(ρ
M
E) − 1
≡ 2p() − 1.
(22.35)
From Schumacher’s (quantum coding) theorem, for any δ>0 and sufficiently long
messages we have p() ≥ 1 −δ, therefore
˜
F ≥ 2 p() −1 ≥ 2(1 −δ) −1 = 1 − 2δ. (22.36)
This final result indicates that for sufficiently long messages, the fidelity
˜
F can be made
arbitrarily close to unity (consistent with the limit δ → 0), which establishes that the
compression code is “reliable.” It is possible to show (but not described here for the sake
of brevity) that any other coding choice, namely with R < S,orR = S − ε (with ε>0,
δ>0), makes the fidelity of sufficiently long messages to be asymptotically bounded
according to
˜
F <δ, which is essentially zero as δ → 0.
22.3 A graphical and numerical illustration of Schumacher’s quantum
coding theorem
In this section, I shall provide an original illustration of Schumacher’s quantum coding,
both graphical and numerical. This will help visualize how the dimension of the typical
subspace asymptotically converges towards 2
nS
, as the message length n increases
and if the parameter ε may be chosen to be arbitrarily small. The numerical application
will also illustrate that there is still a large degree of freedom over the choice of ε and
the typical subspace possibilities to compress quantum messages.
Here, we shall assume the same parameters as in the example used in the two previous
sections, i.e., S(ρ) = 0.6008 for the per-symbol VN entropy, and the two eigenval-
ues λ
a
= 0.8535,λ
b
= 0.1465. For a message length n = 3, we have 2
3
= 8 possible
messages defining an 8D eigenspace . Any of these messages are based on the qubit
permutations of four codeword types of the form |λ
a
λ
a
λ
a
, |λ
a
λ
a
λ
b
, |λ
a
λ
b
λ
b
, |λ
b
λ
b
λ
b
with the respective measurement probabilities λ
3
a
,λ
2
a
λ
b
,λ
a
λ
2
b
,λ
3
b
, in descending order.
Such probabilities also correspond to the eigenvalues: µ
1
= λ
3
a
,µ
2
= µ
3
= µ
4
= λ
2
a
λ
b
,
µ
5
= µ
6
= µ
7
= λ
a
λ
2
b
, and µ
8
= λ
3
b
. According to Eq. (22.37), which I reproduce here
for convenience, we can associate a parameter ε with each of these four groups of
eigenvalues:
+
+
+
+
1
n
log
1
µ
i
− S(ρ)
+
+
+
+
≤ ε. (22.37)
470 Quantum data compression
Message length
n
Parameter
ε
(n,p)
0
0.5
1
1.5
2
2.5
0 1 2 3 4 5 6 7 8 9 10 1112131415161718192021
(
n
,
n
)
ε
(
n
, 0)
ε
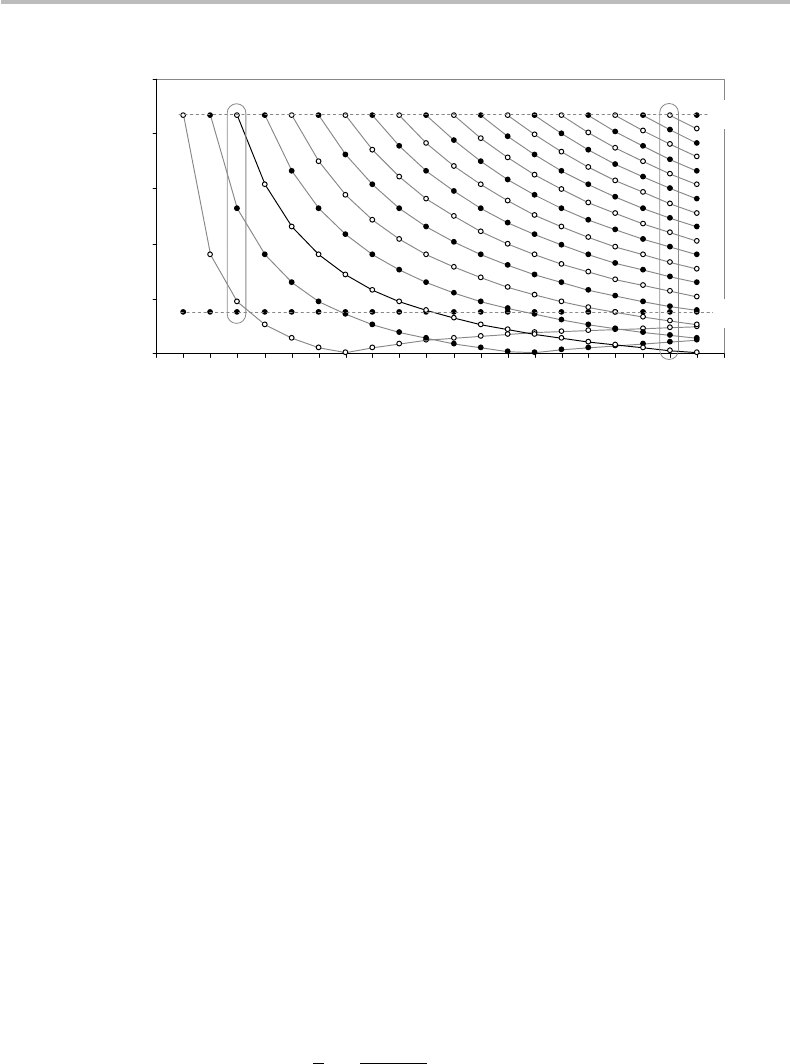
Figure 22.1 Lower bound for the parameter ε(n, p), calculated from Eq. (22.39), in the range
n = 1ton = 20.
Substituting the above values of µ
i
with n = 3 and S(ρ) = 0.6008, we obtain four lower
bounds for ε, namely, to call them by the same letter: ε = 0.372, 0.475, 1.322, 2.170.
As we have seen in the previous section, this calculation does not tell us much as to
how to define a typical subspace. Furthermore, only the first value ε = 0.372 gives a
parameter R < 1 (namely R = S + ε = 0.6008 +0.3724 = 0.9732 < 1), and there is
nothing that we can conclude about any compression potential from such a result! But if
we increase the message length n, and calculate all possible ε values from Eq. (22.37),
we obtain a much broader range of possibilities for the parameter R.
Given the message length n, it is straightforward to tabulate the suite of n + 1 eigen-
values according to the definition
λ
n
a
λ
n−1
a
λ
b
λ
n−2
a
λ
2
b
.
.
.
λ
2
a
λ
n−2
b
λ
n
b
.
(22.38)
The parameter ε(n, p) corresponds to each eigenvalue µ
i
(n, p) = λ
n−p
a
λ
p
b
, as defined
by
+
+
+
+
1
n
log
1
µ
i
(n, p)
− S(ρ)
+
+
+
+
≤ ε(n, p). (22.39)
Figure 22.1 shows the values of the parameter ε(n, p) in the range n = 1ton = 20. The
values are connected by full lines to guide the eye. The top and bottom horizontal lines
correspond to ε(n, n) = ε(µ
i
= λ
n
b
) and ε(n, 0) = ε(µ
i
= λ
n
a
), respectively. The two sets
circled at n = 3 and n = 19 help visualize the effect according to which an increasing
22.3 A graphical and numerical illustration 471
0
0.1
0.2
0.3
0.4
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
Message length
Parameter
ε
(n,p)
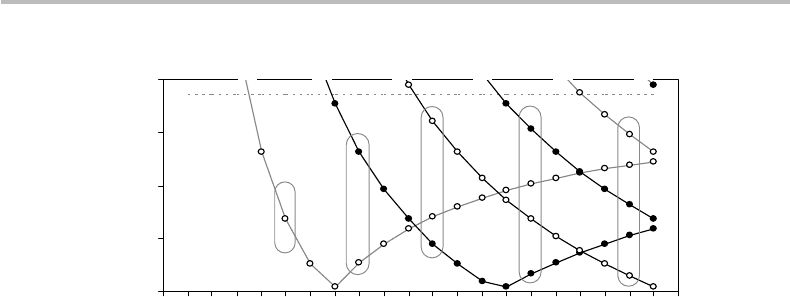
Figure 22.2 Lower bound for the parameter ε(n, p), calculated from Eq. (22.39), with zoom in
the region 0 <ε(n, p) ≤ 0.4.
fraction of the ε(n, p) values progressively form a cluster in the region between ε = 0
and ε(n, 0) ≤ 0.4. This effect is also illustrated in Fig. 22.2, which shows a zoom in
this region. It is clear that for a message length n sufficiently large, any value ε>0 can
be reached by ε(n, p). Furthermore, we observe that given a message length n and any
ε>0 it is always possible to define a subset of codewords satisfying ε(n, p) ≤ ε,as
indicated in the figure by the circled clusters. In the case n = 19, for instance, the cluster
consists of a subset of five codewords satisfying ε(19, p) ≤ 0.29681, and this group of
codewords is precisely the ε-typical subspace we have been looking for! Let us take
a closer look at the corresponding data. Table 22.4 shows, for each codeword type µ of
length n = 19, from left to right: the individual codeword probability p(µ), the number of
possible permutations N of the codeword type µ, the codeword-type probability Np(µ),
the codeword parameter ε, and the associated value R = S + ε. We have defined our
ε-typical subspace as generated by the five codeword types for which ε(19, p) ≤
0.29681. As the table shows, these codeword types are of the form |λ
18
a
λ
1
b
, |λ
17
a
λ
2
b
,
|λ
16
a
λ
3
b
, |λ
15
a
λ
4
b
, and |λ
14
a
λ
5
b
. Summing the N data, it can be found that there exist 16 663
such codewords, out of 524 288 possibilities, representing only about 3% of the codeword
space . Summing the values Np(µ) in the table, one finds that the probability of any
received codeword belonging to this typical subspace is p() = 0.90208, which is
relatively high. This result yields the lower bound δ = 1 − p() = 0.09792 and hence,
using λ
a
= 0.8535, the transmission fidelity
˜
F =
(
1 − δ
)
2
+ δλ
19
a
= 0.81859 ≈ 82%,
which is fair. From the table, we also find that the maximum value of R, or the best
compression factor achievable under this coding scheme, is given by the highest value
of ε in the subspace , namely ε
max
= 0.29681, or R = 0.89769 ≈ 89%.
Having defined the ε-typical subspace (with the choice ε ≤ 0.29681), the next
step is to analyze the effect of increasing the message length n. It is only a matter of
tabulating a spreadsheet that outputs the same data as shown in Table 22.4, along with
the values p(), δ = 1 − p(), and
˜
F =
(
1 − δ
)
2
+ δλ
n
a
, for each value of n. Care must
be taken to effect the summation yielding p() only in the spreadsheet domain where
0 <ε≤ 0.29681. The fidelity
˜
F calculated for message lengths from n = 19 to n = 100

472 Quantum data compression
Table 22.4 Defining an ε-typical subspace with ε ≤ 0.29681, in the case n = 19, corresponding to
a maximum compression R = 0.89769.
Codeword
type µ p(µ) NNp(µ) ε R = S + ε
λ
19
a
λ
0
b
4.936 × 10
−2
1 – 0.37243 0.97330
λ
18
a
λ
1
b
8.469 × 10
−3
19 1.609 × 10
−1
0.23858 0.83946
λ
17
a
λ
2
b
1.453 × 10
−3
171 2.485 × 10
−1
0.10473 0.70561
λ
16
a
λ
3
b
2.493 × 10
−4
969 2.416 × 10
−1
0.02911 0.62999
λ
15
a
λ
4
b
4.277 × 10
−5
3876 1.658 × 10
−1
0.16296 0.76384
λ
14
a
λ
5
b
7.339 × 10
−6
11628 8.534 × 10
−2
0.29681 0.89769
λ
13
a
λ
6
b
1.259 × 10
−6
27132 – 0.43066 1.03153
λ
12
a
λ
7
b
2.160 × 10
−7
50388 – 0.56451 1.16538
λ
11
a
λ
8
b
3.707 × 10
−8
75582 – 0.69835 1.29923
λ
10
a
λ
9
b
6.359 × 10
−9
92378 – 0.83220 1.43308
λ
9
a
λ
10
b
1.091 × 10
−9
92378 – 0.96605 1.56692
λ
8
a
λ
11
b
1.872 × 10
−10
75582 – 1.09990 1.70077
λ
7
a
λ
12
b
3.212 × 10
−11
50388 – 1.23375 1.83462
λ
6
a
λ
13
b
5.511 × 10
−12
27132 – 1.36759 1.96847
λ
5
a
λ
14
b
9.455 × 10
−13
11628 – 1.50144 2.10232
λ
4
a
λ
15
b
1.622 × 10
−13
3876 – 1.63529 2.23616
λ
3
a
λ
16
b
2.783 × 10
−14
969 – 1.76914 2.37001
λ
2
a
λ
17
b
4.775 × 10
−15
171 – 1.90298 2.50386
λ
1
a
λ
18
b
8.193 × 10
−16
19 – 2.03683 2.63771
λ
0
a
λ
19
b
1.406 × 10
−16
1 – 2.17068 2.77156
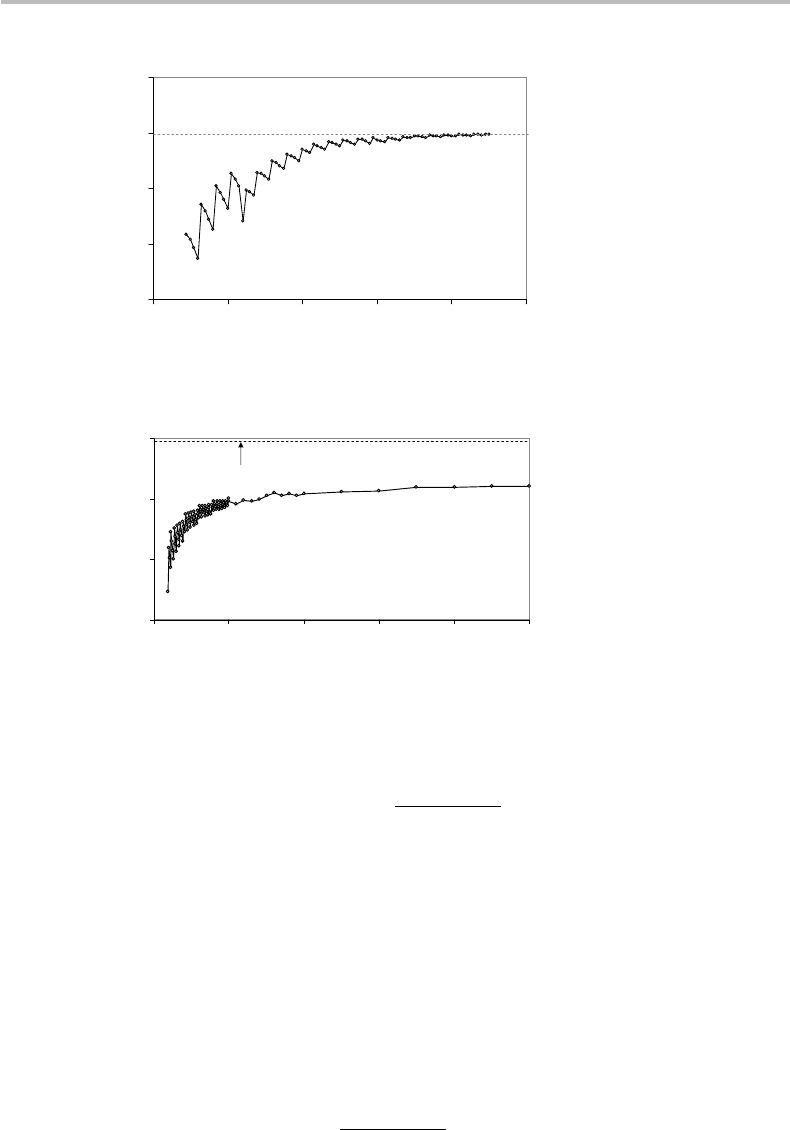
is shown in Fig. 22.3. It is seen that convergence towards 100% fidelity is relatively rapid
(e.g.,
˜
F ≈ 99% or better, for n ≥ 70). Interestingly, such a convergence goes through
sawtooth-like oscillations. These are explained by the irregular variations of the ε(n, p)
cluster size and amplitude previously observed in Fig. 22.2.
The last open issue to discuss is the dimension of the typical subspace, dim(), corre-
sponding to a given message length n.FromEq.(22.28), we know that dim() is bounded
according to (1 −δ)2
n(S−ε)
≤ dim() ≤ 2
n(S+ε)
, which asymptotically becomes 2
nS
as
δ, ε → 0 and with sufficiently long messages. In the most general case (ε>0, any
message length n), we have
S − ε +
log
2
(1 − δ)
n
≤
log
2
[dim()]
n
≤ S + ε.
(22.40)
22.3 A graphical and numerical illustration 473
0.7
0.8
0.9
1.0
1.1
10 30 50 70 90 110
e=<0,29681
Message length
Fidelity
29681
.0≤
ε
Figure 22.3 Fidelity as a function of message length (n = 19 to n = 100), assuming the ε-typical
subspace with ε ≤ 0.29681.
Message length
Parameter ξ(n,Ω)
0.3
0.1
0
0 100 200 300 400 500
0.2
29681.0=
ε
Figure 22.4 Evolution of the parameter ξ(n,) with increasing message length n.
Using the property log
2
(1 − δ)/n ≈ δ/n(ln 2) ≈ 0, we can introduce the parameter ξ
for which the double inequality in Eq. (22.40) is very nearly equivalent to:
ξ(n,) =
+
+
+
+
log
2
[dim()]
n
− S
+
+
+
+
≤ ε. (22.41)
Figure 22.4 shows the evolution of the parameter ξ (n,) with the message length n,
as calculated from our previous example, up to n = 500. For each n, the value dim()
is estimated by summing the values of N (number of ε-typical codewords for which
ε ≤ 0.29681), displayed in the third column in Table 22.4. For clarity, the plot shows
successive data with an increment of one up to n = 100, then with an increment of
10 up to n = 200, then with an increment of 50. The figure shows that the parameter
ξ(n,) asymptotically converges towards the limit ε = 0.29681, which defines the
typical subspace for each n.Wemay,thus,write
lim
n→∞
ξ(n,) = ε
↔
lim
n→∞
log
2
[dim()]
n
= S + ε = R (22.42)
↔
lim
n→∞
dim() = e
n(S+ε)
= e
nR
and since ε can be chosen arbitrarily small, the limiting value for dim()ise
nS
.
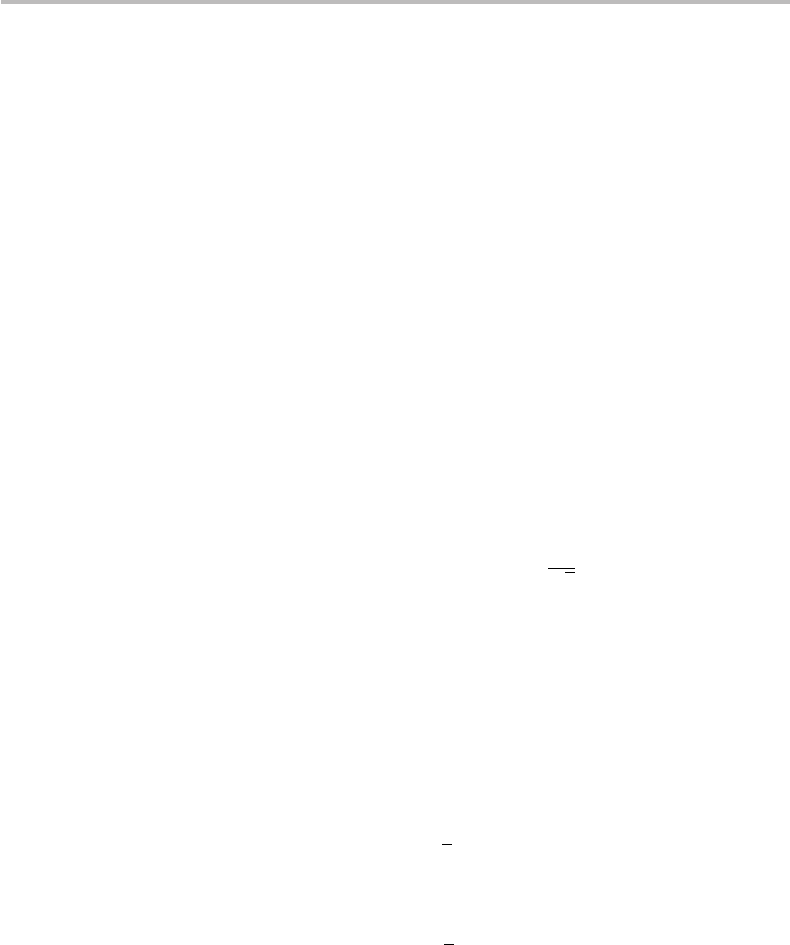
474 Quantum data compression
To summarize, the numerical example developed in this section has shown that given
a message of length n, and any ε>0 such that ε = S − R (with R < 1), there exists a
typical subspace , spanned by a subset of corresponding ε-typical codewords, where
message compression is possible with high fidelity
˜
F. Consistently with the formal
description, the example also showed that (a) for messages of increasing length, the
fidelity
˜
F can be made arbitrarily high, and (b) the dimension of the typical subspace
dim() asymptotically converges towards e
n(S+ε)
. As the parameter ε can be chosen to be
arbitrarily small, the limiting value for the subspace dimension is e
nS
, which corresponds
to the best achievable compression factor R ≈ S.
22.4 Exercises
22.1 (T): Given two tensor states |abc, |def , where |a, |b, |c, |d, |e, | f are
qubits, provide a general formula for the space-overlap factor
|abc
|
def |
2
and apply this formula to all the nine possible cases:
|a, |b, |c=
1
0
≡|α
1
or
1
√
2
1
1
≡|α
2
|d, |e, | f =
cos α
sin α
≡|λ
1
or
−sin α
cos α
≡|λ
2
,
where α is a parameter.
(Clue: refer to the qubit tensor-product definition in Eq. (16.55)asappliedto
the present case.)
22.2 (B): What is the best achievable compression factor for a quantum message of
arbitrary long length, whose qubits are generated by the density operator
ρ =
1
3
13
02
?
22.3 (M): A qubit source is characterized by the density operator
ρ =
1
3
10
02
.
Assuming a quantum message length of n = 5 qubits, determine the ε-typical
subspace and corresponding quantum codewords for which ε = 0.3.

23 Quantum channel noise and
channel capacity
This chapter introduces the notion of noisy quantum channels, and the different types
of “quantum noise” that affect qubit messages passed through such channels. The
main types of noisy channel reviewed here are the depolarizing, bit-flip, phase-flip,
and bit-phase-flip channels. Then the quantum channel capacity χ is defined through
the Holevo–Schumacher–Westmoreland (HSW) theorem. Such a theorem can conceptu-
ally be viewed as the elegant quantum counterpart of Shannon’s (noisy) channel coding
theorem, which was described in Chapter 13. Here, I shall not venture into the complex
proof of the HSW theorem but only provide a background illustrating the similarity
with its classical counterpart. The resemblance with the channel capacity χ and the
Holevo bound, as described in Chapter 21, and with the classical mutual information
H(X ; Y ), as described in Chapter 5, are both discussed. For advanced reference, a hint
is provided as to the meaning of the still not fully explored concept of quantum coherent
information. Several examples of quantum channel capacity, derived from direct appli-
cations of the HSW theorem, along with the solution of the maximization problem, are
provided.
23.1 Noisy quantum channels
The notion of “noisiness” in a classical communication channel was first introduced in
Chapter 12, when describing channel entropy. Such a channel can be viewed schemat-
ically as a probabilistic relation between two random sources, X for the originator, and
Y for the recipient. These sources are defined by symbol alphabets, X ={x
1
, x
2
} and
Y =
{
y
1
, y
2
}
for instance, and their associated probabilities p(x
i
), p(y
j
). An originator
message is, thus, a string of n symbols x
i
∈ X randomly selected from X according
to the distribution p(x
i
), which is transformed at the recipient’s end into a string of n
symbols y
i
∈ Y randomly selected from Y according to the distribution p(y
i
). An ideal
or noiseless channel is such that the knowledge of any symbol x
i
input from the origi-
nator absolutely conditions the knowledge of the symbol y
j
obtained at the recipient’s
end. Thus, for any originator symbol x
i
, there must be a recipient symbol y
j
, such that
p(y
j
|x
i
) = 1 and p(y
j
|x
i=i
) = 0. The set of conditional probabilities p(y
j
|x
i
) can be
put in the form of a transition matrix P(Y |X) and in the case of a noiseless channel with

476 Quantum channel noise and channel capacity
a two-symbol alphabet (binary channel) we must have
P(Y |X) =
10
01
or
01
10
. (23.1)
In the nonideal case where the channel is corrupted by noise, we have p(y
j
|x
i
) = 1 − ε,
where 0 <ε<1 defines the symbol error probability (the probability of mistaking one
symbol for another). The error probability can be the same for the two symbols (binary
symmetric channel), which gives, for instance,
P(Y |X) =
1 − εε
ε 1 − ε
. (23.2)
The above recall from the classical information theory will now help to conceive of the
effect of noise in a quantum communication channel.
As we have seen in Chapter 22, a quantum message M is a “block” represented by
the tensor state |M=|q
1
q
2
...q
n
, with each qubit |q
i
being randomly selected from
a given symbol alphabet {|x
k
}
k=1...N
of size N . Given the fact that each symbol |x
k
is
associated with an occurrence probability p
k
, it is possible to define a symbol density
operator according to:
ρ =
N
k=1
p
k
|a
k
a
k
|. (23.3)
Consistently, the full symbol block of length n is characterized by the density operator:
ρ
M
= ρ ⊗ ρ ⊗ ...⊗ ρ ≡ ρ
⊗n
, (23.4)
which represents the originator’s message M. As with the definition of a density operator,
we have tr(ρ
M
) = 1. Consequently, some message σ
M
may be received at the recipient’s
end. The correspondence between the originator’s and the recipient’s messages may be
defined through a transformation, or quantum operation, ε, such that
σ
M
= ε(ρ
M
). (23.5)
Such a quantum operation ε must be trace preserving, so that σ
M
is a density operator
with tr(σ
M
) = 1. Since the message transformation from originator to recipient is fully
defined by the operation ε, it is customary to refer to ε as the quantum channel itself.
In the ideal or “noiseless” case, one would expect that the quantum channel ε corre-
sponds to some unitary (trace-preserving) transformation U , which gives
σ
M
= ε(ρ
M
) = U
+
ρ
M
U. (23.6)
Thus, according to the above operation the message is not invariant by transmission
through the quantum channel (σ
M
= ρ
M
), but its integrity is fully conserved. Indeed,
it only takes the recipient to apply the inverse operation ε
−1
defined by U
−1
= U
+
to
the received message σ
M
, to obtain σ
M
= ε
−1
(σ
M
) = U σ
M
U
+
≡ ρ
M
and, hence, fully
retrieve the originator’s message. A trivial case of ideal or noiseless channel is given
by U = I
⊗n
, where I is the 2 × 2 identity matrix. A more general definition for any
