Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

21.2 Relative, joint, and conditional entropy, and mutual information 447

It is clear by comparison with Eq. (21.56) that ρ

= ˆρ

⊗ ˆρ

, meaning that, in the

present example, the tensor product ˆρ

⊗ ˆρ

of the reduced density operators ˆρ

, ˆρ

does not correspond to the density operator of the composite system. This is not a

surprise, since we established earlier that the joint state |ψ

 cannot be reduced to a

tensor product.

Pushing curiosity further, we may calculate the quantum information,

S(ˆρ

), S(ˆρ

⊗ ˆρ

) associated with the reduced density operators ˆρ

, ˆρ

, and

ˆρ

⊗ ˆρ

, to ﬁnd:

S(ˆρ

) = S(ˆρ

)

=−(1/6) log(1/6) − (5/6) log(5/6)

≡ 0.650,

S(ˆρ

⊗ ˆρ

) =−2 ×(5/36) log(5/36) − (1/36) log(1/36) −(25/36) log(25/36)

≡ 1.300

≡ S(ˆρ

) + S(ˆρ

(21.62)

Based on the information knowledge of the composite system, S(ρ

) = 1.251, as

established in Eq. (21.56), we ﬁnd that:

S(ρ

) = 1.251

< S(ˆρ

) + S(ˆρ

)

= 1.300.

(21.63)

This result is consistent with the subadditivity inequality established earlier and for-

malized in Eq. (21.28). It is also consistent with the triangle inequality deﬁned in

Eq. (21.43). We may, thus, conclude, as a postulate but not as a formal demonstration,

that S(ˆρ

), S(ˆρ

) indeed represent the quantum information contents of the two subsys-

tems A, B, despite the fact that the density operator of the composite system, ρ

, does

not reduce to the tensor product ˆρ

⊗ ˆρ

Without realizing it, this example and postulate helped make great progress in the

analysis of information correlation! Indeed, we can now apply the deﬁnition of quantum

mutual information in Eq. (21.38) to obtain in this example:

S(ρ

; ρ

) = S(ˆρ

) + S(ˆρ

) − S(ρ

)

= 1.300 − 1.251

= 0.049.

(21.64)

We can, thus, conclude that quantum information in subsystems A, B is correlated,as

expressed by the mutual information S(ρ

; ρ

) = 0.049, corresponding to about 0.05

classical bit. From Eq. (21.39), we ﬁnd the conditional entropy:

S(ρ

|ρ

) = S(ρ

) − S(ˆρ

)

= 1.251 − 0.650

= 0.601

(21.65)

with S(ρ

|ρ

) = S(ρ

|ρ

). The knowledge of the information in one of the sub-

systems, thus, decreases the information (or uncertainty) in the other system by the

448 Quantum information theory

amount S(ρ

) − S(ρ

|ρ

) = 0.650 −0.601 = 0.049 = S(ρ

; ρ

), which corresponds

to the mutual information in the composite system.

Example 21.3: Composite system in pure state

As a ﬁnal example, consider the joint state

|ψ

=

√

(|00+|11)

. (21.66)

This state, which is also noted |β

, is one of the four Bell–EPR states (see Eqs. (16.2)

and (18.15)). As we have learnt, the Bell–EPR states cannot be generated by the tensor

product of two qubits, and they also form an orthonormal basis in the 2-qubit space

(referred to as {|β

, |β

}). In this basis, |ψ

=|β

 is, thus, a pure

state and its density operator is, therefore, equal to ρ

=|ψ

ψ

|. Substitution

of the deﬁnition in Eq. (21.66) and rearrangement of the different terms into tensor

products yields:

=|ψ

ψ

(|00+|11)

⊗ (00|+11|)

(|0000|+|0011|+|1100|+|1111|)



|00|

⊗|00|

+|01|

⊗|01|

+|10|

⊗|10|

+|11|

⊗|11|



(21.67)

Next, we calculate the reduced density operators ˆρ

= tr

(ρ

) and ˆρ

= tr

(ρ

while using the property with the property tr(|ij|) =i |j≡δ

, to obtain:

ˆρ

= tr

(ρ

)



|00|

tr(|00|

) +|01|

tr(|01|

)

+|10|

tr(|10|

) +|11|

tr(|11|

)



(|00|

+|11|

)

≡

(21.68)

ˆρ

= tr

(ρ

)

[

tr(|00|

) ×|00|

+ tr(|01|

) ×|01|

+ tr(|10|

)

×|10|

+ tr(|11|

) ×|11|

]

(|00|

+|11|

)

≡

(21.69)

where I

, I

are the identity matrices of subsystems A, B. We observe that tr( ˆρ

) =

tr( ˆρ

) = 1/2 < 1, which shows that ˆρ

, ˆρ

correspond to mixed states. For the sake of

21.2 Relative, joint, and conditional entropy, and mutual information 449

curiosity, let us now calculate the tensor product ˆρ

⊗ ˆρ

from Eqs. (21.68) and (21.69).

We obtain

ˆρ

⊗ ˆρ

⊗

≡

(|0000|+|0101|+|1010|+|1111|).

(21.70)

Comparison between Eq. (21.70) and Eq. (21.67) shows that, as expected, ρ

= ˆρ

⊗

ˆρ

. This provides an indication that the information in the subsystems A, B is correlated

or, equivalently, that the subsystem states are entangled.

Next, we calculate the quantum information, S(ˆρ

), S(ˆρ

) associated with the reduced

density operators ˆρ

, ˆρ

, to ﬁnd:

S(ˆρ

) = S(ˆρ

) =−2 ×(1/2) log(1/2) ≡ 1. (21.71)

Thus, each of the subsystems A, B has a quantum information equivalent to exactly

one classical bit, which corresponds to the qubit state |q=(|0±|1)/

√

2 of maximal

uncertainty. Such a conclusion is also consistent with our previous observation according

to which the two subsystems A, B must be in mixed states (tr( ˆρ

) = tr( ˆρ

) = 1/2 < 1).

The situation of the two subsystems, A, B, contrasts with that of the composite system,

AB, which is in the pure state |β

. By deﬁnition, this state is known exactly and,

therefore, it has zero quantum information, meaning that S(ρ

) = 0. This is a most

intriguing feature, without any counterpart in the classical world: there is no information

in the composite system, while there is maximal information in the two subsystems!

Formally, we obtain for the mutual information and the conditional entropy:

S(ρ

; ρ

) = S(ˆρ

) + S(ˆρ

) − S(ρ

)

= 1 + 1 −0 = 2,

(21.72)

S(ρ

|ρ

) = S(ρ

) − S(ˆρ

) = 0 − 1 ≡−1

S(ρ

|ρ

) = S(ρ

) − S(ˆρ

) = 0 − 1 ≡−1.

(21.73)

These results show that the two subsystems have the equivalent of two classical bits

(two cbits) for mutual information, which shows that the 1-cbit information they each

possess in fact constitute shared property! On the other hand, knowledge of the infor-

mation contents of one subsystem removes one cbit from the information in the other

subsystem, as the conditional entropy is negative. Since the other subsystem has one

cbit of information content, there is actually no information left to measure! This obser-

vation means that knowledge of one subsystem exactly conditions that of the other,

which illustrates the principle of quantum entanglement. Another way to understand

this conditioning property is to consider the effect of measuring the information in one

of the two subsystems. Assume, for instance, that our measurement ﬁnds subsystem A

in the state |0. The post-measurement state, which now characterizes subsystem B,is

the pure state |ψ

=|0

. If our measurement ﬁnds subsystem A in the state |1,the

post-measurement state is the pure state |ψ

=|1

. Either measurement in subsystem

450 Quantum information theory

A, thus, results in the collapse of subsystem B into a pure state. The same conclusion

strictly applies if subsystem B is measured ﬁrst. Thus, in all possible cases, a measure-

ment of one subsystem collapses the other into a pure state, which, as we know, contains

zero information.

As we have seen in Chapter 18, quantum entanglement, as a characteristic property

of the Bell–EPR states, can be used for the purpose of quantum teleportation. See more

illustrations of the effect of quantum entanglement in the exercises.

21.3 Quantum communication channel and Holevo bound

We may now conceive a quantum version of Shannon’s communication channel

(Chapter 11), with the purpose of transmitting information from an originator entity

to a recipient entity. Here, the words “communication” and “transmission” should not

be interpreted in the engineering meaning of sending information through a wire from

one point to another over some distance. Instead, the strict meaning is that of a message

being communicated in some coded form, from an originator to a recipient, regardless

of the physical transmission means, the overall channel being a quantum system.Letme

now clarify how such a channel may be operated.

As in the classical case, the information is encapsulated into a message X, which

represents a succession of symbols (or letters,orcodewords), x, to be encoded by

the originator from a possible alphabet (or code) of size n. The message symbols are

associated with a probability p

. After passing through a physical “transmission pipe,”

the symbols are then decoded by the recipient, to restore the classical information therein.

In the quantum case, however, the information is to be carried by quantum states, which

will now be referred to by their density operators ρ

. From the simplest perspective, the

operation of encoding consists, for the originator, of the “preparation” of the quantum

states, ρ

, which is made according to the message’s probability distribution p

. Here,

the word “preparation” means setting up the conditions for a given quantum system to

be exactly in the state ρ

. The operation of decoding is, for the recipient, the action

of performing “measurements” on each of the received quantum states. According

to Chapter 17, such measurements can be made through a collection of n Hermitian

operators {E

}

m=1...n

referred to as a POVM set. The outcome of any measurement is a

real positive number y belonging to some alphabet Y of size n. We note that from this

description, X, Y are classical sources with x, y as associated random events, while the

communication channel is quantum.

I shall now focus on the mutual information, H(X ; Y ) associated with the above-

described quantum communication channel. A key property is that the mutual informa-

tion is bounded by a maximum, χ, referred to as a Holevo bound, and deﬁned by

H(X ; Y ) ≤ S(ρ) −



S(ρ

) = χ, (21.74)

21.3 Quantum communication channel and Holevo bound 451

where ρ =



=ρ is the mean density operator, as averaged over the coding

possibilities. Based on this notation, and combining Eq. (21.74) with the general property

of concavity of entropy in Eqs. (21.50) and (21.51), the Holevo bound condition also

gives

H(X ; Y ) ≤ χ ≤ H (X ), (21.75)

where H (X ) is the Shannon entropy of the originator message source. In a clas-

sical communication channel, the mutual information cannot exceed the entropy of

the originator source, namely H (X; Y ) = H (X) − H (X|Y ) with H (X|Y ) ≥ 0 (see

Chapter 5), hence, H (X; Y ) ≤ H (X). Thus, Eq. (21.74) is granted. However, the inter-

mediate Holevo bound χ in this equation is nontrivial, except in the case χ = H (X ),

corresponding to the speciﬁc situation where ρ

have support on orthogonal states. In

the contrary case, we have χ<H(X) and, hence, the condition H(X; Y ) < H(X ). In

such a condition, there exists no possibility for the recipient to completely recover the

originator’s information H (X) through any set of measurements on Y . This constitutes

a nonintuitive situation that cannot be experienced from any “classical viewpoint.”

The formal proof of the Holevo bound is presented in Appendix X. The proof is

tractable but, unfortunately, only to a certain extent! As described in this appendix,

indeed, the full proof requires the introduction of an additional entropy property referred

to as strong subadditivity.

Such a property, which has not be described in the earlier

subsection, rests on two additional theorems, whose demonstration is rather mathe-

matically involved. For this reason, and for the purpose of these chapters, we shall

take “strong subadditivity” as a granted postulate. Going through the derivations in

Appendix X, however, should not be viewed as a vain exercise. Rather, in addition to

coming very close to an intuitive (albeit incomplete) proof of the Holevo bound, it also

represents an opportunity to familiarize oneself with the concept of quantum operations,

of which quantum measurements with POVM operators represent a very representative

illustration.

I shall now illustrate the consequences of the Holevo bound through a few basic

examples.

Example 21.4: A “useless” quantum communication channel

Assume that the originator is able to prepare a quantum system in two possible orthog-

onal states |q

=(|0+|1)/

√

2 and |q

=(|0−|1)/

√

2, but with some relative

uncertainty, according to a probability law deﬁned by p

= p and p

= 1 − p.Not

being 100% certain, these two states are mixed states, having the corresponding and

The property of “strong subadditivity” states that for any three quantum systems A, B, C, the following

inequalities hold:

S(A) + S(B) ≤ S(A, C) + S(B, C)

S(A, B, C) + S(B) ≤ S(A, B) + S(B, C).

452 Quantum information theory

equal density operators:

= ρ

(|00|+|11|) =

. (21.76)

The mean density operator is ρ = pρ

+ (1 − p)ρ

= ρ

. Clearly, the VN

entropy is the same for the three states ρ,ρ

,ρ

, i.e., S(ρ) = S(ρ

) = S(ρ

) =−2 ×

(1/2) log(1/2) = 1, hence, the Holevo bound χ is zero, meaning H(X ; Y ) = 0. Such

a quantum communication channel has no mutual information available whatsoever in

reserve and, in the sense of information theory, is, therefore, useless. Formally, this use-

lessness characteristic is because the qubit states used for the message quantum states,

albeit orthogonal as “symbols,” have strictly identical supports (or eigenstate spaces).

Basically, the originator does not have any control on his or her source to prepare any

“communicable” information. Based on the fact that each of the proposed qubits con-

tain exactly one classical bit (cbit), and that the two are orthogonal, this conclusion of

uselessness sounds like a disillusionment concerning the communication potential. But

it is now clear that their mixed-state nature render the communication attempt useless,

no matter what the distribution deﬁned by the parameter p.

Example 21.5: A quantum communication channel reduced to classical

The originator (based on the previous experience) is now able to prepare his or her

quantum system with the same orthogonal qubits, i.e., |q

=(|0+|1)/

√

2 and |q

=

(|0−|1)/

√

2, but this time as pure states, contrary to the previous example. This

means that in each possible preparation, there is absolute certainty that the outcome

is either |q

 or |q

, as required. Then the two preparations that can be chosen have

corresponding density-operators:

(|0+|1)(0|+1|) =





→





(|0−|1)(0|−1|) =



1 −1

−11



→





(21.77)

In the above, the arrows mean in each case that the density matrix is transformed

from the basis {|0, |1} into the eigenstate basis {|+, |−} = {|q

, |q

}. The origi-

nator then selects the qubits according to the message’s probability law, here deﬁned

by p

= p and p

= 1 − p, where p is a parameter. The mean density operator is,

therefore,

ρ = pρ

+ (1 − p)ρ



p 0

01− p



. (21.78)

Clearly, we have for the VN entropy S(ρ) =−[p log p − (1 − p)log(1− p)] = f ( p) ≡

H(X ) and S(ρ

) = S(ρ

) = 0 (pure states). Thus, the Holevo bound is χ = f (p) =

H(X ) meaning H(X ; Y ) ≤ H (X ) as in the case of a classical communication channel.

We note that the strict equality for the Holevo bound, χ = H (X ), stems from the fact that

21.3 Quantum communication channel and Holevo bound 453

the message states ρ

,ρ

have orthogonal support. This result shows that the quantum

communication channel is able to convey information that can be up to H(X ), which

is the classical entropy of the originator’s message source. Interestingly, the quantum

“symbols” carry no information by themselves, since S(ρ

) = S(ρ

) = 0arepurestates.

As we know, H (X) is maximized for the choice p = 0.5, corresponding to a coin-tossing

probability law.

Example 21.6: General case

This example represents an interesting generalization of the previous situation. The

originator is able to prepare single qubits as pure states, and the message to be encoded

is a long string of 1 or 0 cbits with a uniform probability distribution. If the cbit is 0, the

qubit symbol is chosen, for instance, to be |0, and if the cbit is 1, the qubit symbol is

chosen to be cos θ|0+sin θ|1, where θ ∈ [0,π] is an arbitrary parameter. The density

operators of the message’s qubit symbols are











=|00|=





= (cos θ|0+sin θ |1)(cos θ 0|+sin θ1|)

= cos

θ|00|+cos θ sin θ|01|+cos θ sin θ |10|+sin

θ|00|



cos

θ cos θ sin θ

cos θ sin θ sin



(21.79)

Each qubit symbol having the same probability p

= p

= 1/2, we obtain for the mean

density operator:

ρ =



i=1







cos

θ cos θ sin θ

cos θ sin θ sin



≡



1 + cos

θ cos θ sin θ

cos θ sin θ sin



(21.80)

It is easily found through the characteristic equation that the eigenvalues of ρ are

1,2

= (1 ± cos θ )/2, or λ

= cos

(θ/2) and λ

= sin

(θ/2) = 1 − λ

. The VN entropy

of the originator’s quantum source (ρ) is, therefore:

S(ρ) =−λ

log λ

− λ

log λ

=−λ

log λ

− (1 −λ

)log(1− λ

)

≡ f (λ

)

≡ f [cos

(θ/2)].

(21.81)

Since S(ρ

) = S(ρ

) = 0 (pure states) the Holevo bound is

χ = S(ρ) = f



cos



. (21.82)

A plot of the above-deﬁned Holevo bound is provided in Fig. 21.1. It is seen that a

maximum is reached for x = 0.5orθ = π/2, which corresponds to a choice for the

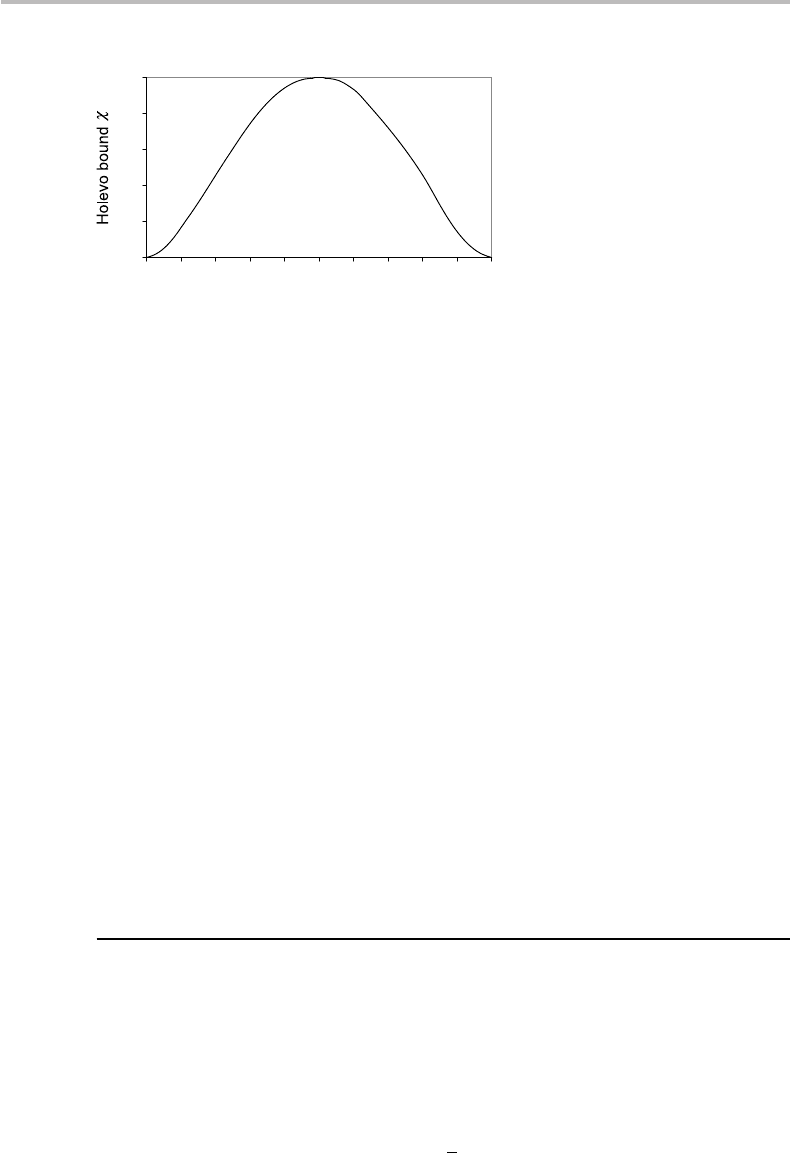
454 Quantum information theory

q/p

0.1

0.2

0.4

0.6

0.8

0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Figure 21.1 Holevo bound χ as a function of the argument θ, showing a maximum at θ = π/2.

second qubit of |q

=|1 or ρ

=|11|. In this case, H(X ; Y ) ≤ χ = H (X) = 1,

meaning that information can be transmitted through the quantum channel up to

1 bit, corresponding to the originator’s source entropy. In any other case, or θ = π/2,

the Holevo bound is less than unity (the originator’s source entropy) and there is no

possibility for the original information to be fully retrieved by the recipient. Clearly,

such a limitation is attributable to the fact that the set of density operators used to code

the symbols does not have orthogonal support, meaning that they have a ﬁnite overlap,

deﬁned formally as |q

|

= cos

θ = 0. The case θ = π/2, where the two states

, |q

 are orthogonal, reduces the quantum channel to a classical one, as described

in Example 2.

In summary, the key lesson to retain from the above description and examples is

that it is possible to transmit (or “convey”) classical information through a quantum

communication channel. A prerequisite is that the alphabet of quantum symbols used to

code information must be made of pure states, in which case the Holevo bound χ equals

the VN entropy or average quantum information per symbol (χ = S(ρ)). A second,

optional, requirement is that the alphabet states be orthogonal, in which case the Holevo

bound is maximized and is equal to the originator’s source entropy (χ = H(X )). In any

case, the mutual information H (X; Y ), i.e., the amount of information that the originator

and the recipient may be able to share, satisﬁes H (X; Y ) ≤ χ .

The concept of the quantum communication channel will be revisited in Chapter 23,

which considers the effect of channel corruption by quantum noise.

21.4 Exercises

21.1 (B): Show that the quantum system with density matrix (basis representation

{|0, |1})

ρ =





21.4 Exercises 455

corresponds to the pure state

|+ =

√

(|0+|1).

21.2 (B): Show that the density operator ρ =|00| of a pure state |0 can be trans-

formed into the basis {|+, |−} with the deﬁnition (using here the sign ⊕ for

clarity in the summation):

˜ρ =

(|++| ⊕ |+−| ⊕ |−+| ⊕ |−−|)

|+ ⊕ |−

√

⊗

+|⊕−|

√

21.3 (B): Show that for any density operator ρ, the property

tr(ρ

) ≤ 1

applies with equality only for the case of pure states.

21.4 (M): Given a quantum system with the density matrix

ρ =





determine the corresponding state |ψ in the eigenstate basis and the von Neu-

mann entropy.

21.5 (M): Given the density matrices ρ

,ρ

and identity matrices I

, I

of two subsys-

tems A, B with dimensions n × n and p × p, respectively, and the density matrix

of the joint system with dimension n × p, show the following relations:

(1) ρ

⊗ ρ

= (ρ

⊗ I

)(I

⊗ ρ

(2) log(ρ

⊗ ρ

) = log(ρ

) ⊗ I

+ I

⊗ log(ρ

and

(3)



tr[ρ

log(ρ

⊗ I

)] = tr(ρ

log ρ

)

tr[ρ

log(I

⊗ ρ

)] = tr(ρ

log ρ

using for (3) the property valid for any observable U

in a composite system XY

tr[ρ

⊗ I

)] = tr(ρ

)

with a similar relation applying to any observable U

(Clue: start from the operator tensor-product deﬁnition in Eq. (16.54), and assume,

for simplicity and without loss of generality, that n = 2, p = 3)

21.6 (B): Show that the 2-qubit state

|ψ=

√

(|00+|10+|11)

456 Quantum information theory

(a) Is not a pure state;

(b) Cannot be decomposed as a tensor product |ψ

⊗|ψ

 of some subsystem

states |ψ

, |ψ

.

21.7 (M): Determine the von Neumann entropy of the composite system having density

operator

ρ =

(|0000|+|0011|+2|1010|+|1100|+|1111|).