Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


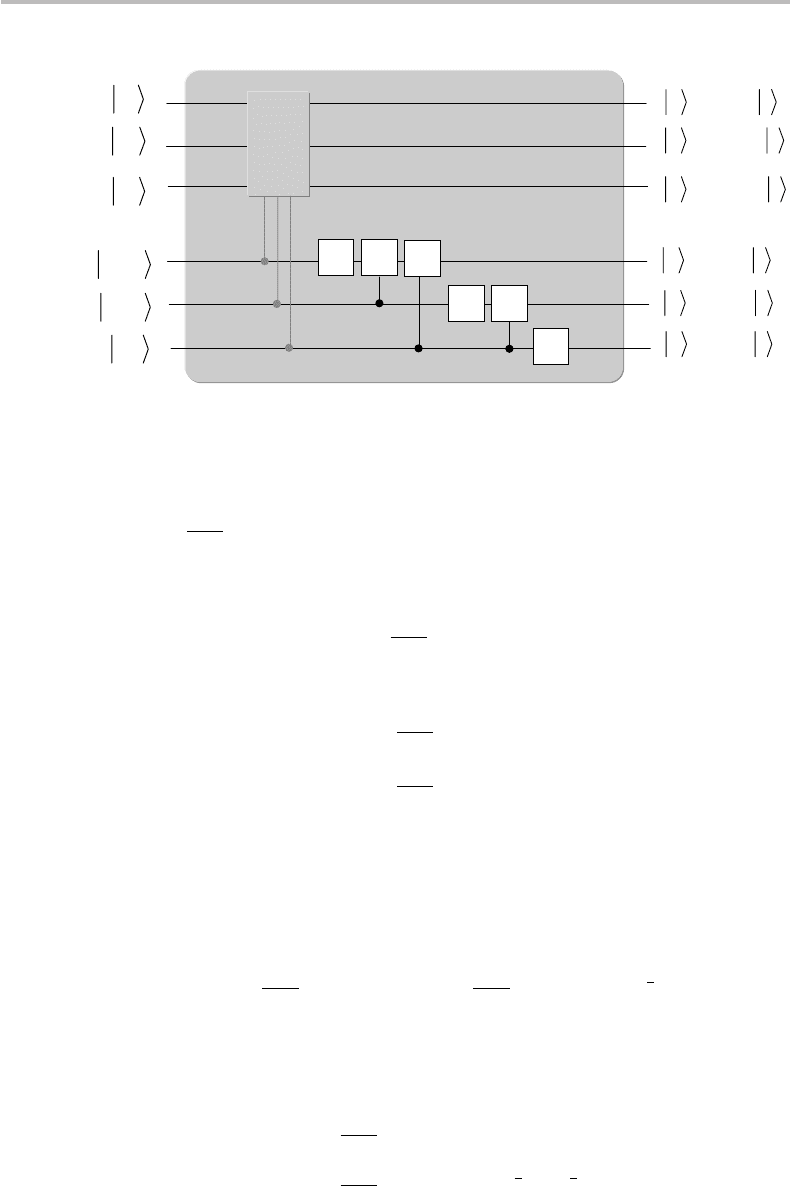
Appendix P (Chapter 18) Two-qubit
teleportation
In this appendix, I formally demonstrate the possibility of simultaneously teleporting two
qubits from Alice’s location to Bob’s. The proposed six-qubit quantum circuit, shown in
Fig. P1, is an original, symmetrical variant of that described in Gottesman and Chuang
(1999).
1
Such an example also represents a test case for the analysis of quantum circuits
and Bell measurements, as a full illustration of the concepts and formalism described in
Chapter 18, hence, the detailed calculations presented here.
In the circuit shown in Fig. P1, the boxes B, B
stand for Bell-state measurements
and X
n
, X
n
, Z
n
, Z
n
are Pauli gates controlled by classical bits n, m, n
m
. The inputs
|q
1
, |q
6
are two qubits from Alice, who accesses the quantum wires 1, 2, 5, and 6. Bob
only has access to the quantum wires 3 and 4, where he retrieves the teleported qubits
under the tensor state |ψ=CNOT|q
3
|q
4
= C
43
|q
3
⊗|q
4
, as illustrated in Fig. P1
(applying a second CNOT, allowing Bob to retrieve Alice’s individual qubits |q
3
, |q
4
).
For the teleportation, Alice and Bob share a 4-qubit entangled state |χ , defined by
|χ=
1
4
(|0000+|0111+|1100+|1011)
2345
(P1)
(the circuit used to generate |χ, which entangles two Bell states |β
00
is shown in
Fig. 18.11).
We proceed now to the formal demonstration of the 2-qubit teleportation effect that
is achieved through the above-described circuit. To analyze the qubit evolution in pre-
and post-measurement stages, we need first to detail the Bell-state measurement circuits
B, B
. Such circuits are shown in Fig. 18.5, and reproduced in Fig. P2 according to the
circuit notations.
In the figure, the term C
ij
designates CNOT gates where i is the control qubit, j is
the target qubit, and H
k
are Hadamard gates placed on the quantum wire k.Thetwo
Bell-measurement apparatuses B, B
output the post-measurement classical bits n, m
and n
m
, respectively, which correspond to pure states |nmn
m
1256
, to be defined later.
Our task now is to calculate the 6-qubit state situated just past the two Hadamard gates
in B, B
and ahead of Alice’s two measurements. This will allow us to know what post-
measurement states |nmn
m
⊗|∗
23
are to be expected, and hence, the action of the
X
n
, X
n
, Z
n
, Z
n
gates based on Bob’s knowledge of the four classical bits n, m, n
m
.
1
D. Gottesman and I. L. Chuang, Quantum teleportation is a universal computational primitive. Nature, 402
(1999), 390–3, http://arxiv.org/PS_cache/quant-ph/pdf/9908/9908010v1.pdf.

638 Appendix P
q
χ
´
q
B
´
4
n
X
ψ
B
1
2
3
4
5
6
m
n
´
n
´
m
´
3
n
X
m
Z
4
m
Z
3
´
B
n
X
3
´
4
m
Z
q
´
q
ψ
Figure P1 Six-qubit quantum circuit for teleporting two qubits.
1
H
1
q
2
χ
n
m
B
5
H
6
´
q
5
χ
´
m
´
n
´
B
12
C
56
C
Figure P2 Principle of Bell measurement or measurement in Bell state.
We then define Alice’s two qubits as:
|q
1
≡ α|0+β|1
|q
6
≡ α
|0+β
|1,
(P2)
and based on the definition of |χ in Eq. (P1), we develop the 6-qubit tensor | that is
input to the circuit, as follows (overlooking normalization factors):
|=|q
1
⊗|χ
2345
⊗|q
6
= (α|0
1
+ β|1
1
) ⊗ (|0000+|0111+|1100+|1011)
2345
⊗|q
6
=
3
α|00000+α|00111+α|01100+α|01011+
β|10000+β|10111+β|11100+β|11011
4
12345
⊗|q
6
=
3
α|00000+α|00111+α|01100+α|01011+
β|10000+β|10111+β|11100+β|11011
4
12345
⊗ (α
|0
6
+ β
|1
6
)
=
αα
(|000000+|001110+|011000+|010110) +
αβ
(|000001+|001111+|011001+|010111) +
α
β(|100000+|101110+|111000+|110110) +
ββ
(|100001+β|101111+|111001+|110111)
123456
.
(P3)
We must then apply the action of the two CNOT gates C
12
, C
56
in B, B
, noted C
12
, C
56
respectively, with the first and second indices representing the control and target qubits.

Two-qubit teleportation 639
For any binary combinations a, b, c, d, e, f =
{
0, 1
}
in a 6-qubit state |abcdef ,itis
clear that the gates have the corresponding action:
C
12
|0abcde=|0abcde
C
12
|1abcde=|1
¯
abcde
C
56
|abcd0e=|abcd0e
C
56
|abcd1e=|abcd1
¯
e.
(P4)
Effecting the above rules in Eq. (P3), we obtain |
=C
56
C
12
| as:
|
=
αα
(|000000+|001111+|011000+|010111) +
αβ
(|000001+|001110+|011001+|010110) +
α
β(|110000+|111111+|101000+|100111) +
ββ
(|110001+|111110+|101001+|100110)
123456
. (P5)
Next, we must calculate the action of the subsequent Hadamard gates H
1
, H
5
acting on
qubits 1 and 5, respectively, recalling first that
H|0=|+=
|0+|1
√
2
H|1=|−=
|0−|1
√
2
,
(P6)
and, hence, for any binary combination a, b, c, d, e =
{
0, 1
}
:
H
1
|0abcde=|+abcde=
|0abcde+|1abcde
√
2
H
1
|1abcde=|−abcde=
|0abcde−|1abcde
√
2
H
5
|abcd0e=|abcd + e=
|abcd0e+|abcd1e
√
2
H
5
|abcd1e=|abcd − e=
|abcd0e−|1abcd1e
√
2
.
(P7)
Applying the two Hadamard gates H
1
, H
5
onto |
in Eq. (P5), and overlooking the
normalization factor, we obtain |=H
5
H
1
|
,as:
|=
αα
(|+000 + 0+|+011 −1+|+110 +0+|+101 −1) +
αβ
(|+000 + 1+|+011 −0+|+110 +1+|+101 −0) +
α
β(|−100 +0+|−111 − 1+|−010 +0+|−001 −1) +
ββ
(|−100 + 1+|−111 −0+|−010 +1+|−001 −0)
123456
, (P8)

640 Appendix P
where the states |± are defined in Eq. (P6). Substituting these definitions in Eq. (P8),
but in two steps to avoid mistakes, the result decomposes itself into 64 6-qubits:
|
=
αα
|0000 + 0+|1000 + 0+
|0011 − 1+|1011 − 1+
|0110 + 0+|1110 +0+
|0101 − 1+|1101 − 1
+ aβ
|0000 +1+|1000 + 1+
|0011 −0+|1011 − 0+
|0110 +1+|1110 + 1+
|0101 −0+|1101 − 0
+α
β
|0100 + 0−|1100 + 0+
|0111 − 1−|1111 − 1+
|0010 + 0−|1010 + 0+
|0001 − 1−|1001 − 1
+ ββ
|0100 +1−|1100 + 1+
|0111 −0−|1111 − 0+
|0010 +1−|1010 + 1+
|0001 −0−|1001 − 0
123456
=
αα
|000000+|000010+|100000+|100010+
|001101−|001111+|101101−|101111+
|011000+|011010+|111000+|111010+
|010101−|010111+|110101−|110111
+αβ
|000001+|000011+|100001+|100011+
|001100−|001110+|101100−|101110+
|011001+|011011+|111001+|111011+
|010100−|010110+|110100−|110110
123456
+
α
β
|010000+|010010−|110000−|110010+
|011101−|011111−|111101+|111111+
|001000+|001010−|101000−|101010+
|000101−|000011−|100101+|100111
+ββ
|010001+|010011−|110001−|110011+
|011100−|011110−|111100+|111110+
|001001+|001011−|101001−|101011+
|000100−|000110−|100100+|100110
123456
. (P9)
Note that the above development is far more easily obtained using a math-equation
editor than through handwriting calculation. Yet, the operation requires extreme care
in the different character substitutions. I shall now regroup the 64 terms in Eq. (P9)
according to the 16 possible base elements |mnm
n
1256
for the combined Bell-
measurement bases, which, for clarity, I order in binary progression of the indices
mnm
n
= 0000, 0001, 0010, 0011 ...,as:
|mn
12
⊗|m
n
56
≡|mnm
n
1256
=
|0000
1256
, |0001
1256
, |0010
1256
, |0011
1256
,
|0100
1256
, |0101
1256
, |0110
1256
, |0111
1256
,
|1000
1256
, |1001
1256
, |1010
1256
, |1011
1256
,
|1100
1256
, |1101
1256
, |1110
1256
, |1111
1256
,
. (P10)
Note that I choose here to label the base states according to |mnm
n
1256
, which is
arbitrary but will make sense further on. To lighten the notations, in the following I shall
write
|mnabm
n
123456
≡|mnm
n
|ab
34
. (P11)

Two-qubit teleportation 641
Factoring the terms, first according to |ab
34
, and then according to |mnm
n
we obtain:
|=
αα
(|0000+|0010+|1000+|1010)|00
34
+
(|0001+|0011+|1001+|1011)|11
34
+
(|0100+|0110+|1100+|1110)|10
34
+
(|0101+|0111+|1101+|1111)|01
34
+αβ
(|0001+|0011+|1001+|1011)|00
34
+
(|0000+|0010+|1000+|1010)|11
34
+
(|0101+|0111+|1101+|1111)|01
34
+
(|0100+|0110+|1100+|1110)|01
34
α
β
(|1000+|0110+|1100+|1110)|00
34
+
(|0101+|0111+|1101+|1111)|11
34
+
(|0000+|0010+|1000+|1010)|10
34
+
(|0001+|0011+|1001+|1011)|01
34
+ββ
(|0101+|0111+|1101+|1111)|00
34
+
(|0100+|0110+|1100+|1110)|11
34
+
(|0001+|0011+|1001+|1011)|10
34
+
(|0000+|0010+|1000+|1010)|01
34
=
|0000(αα
|00+αβ
|11+α
β|10+ββ
|01
34
) +
|0001(αβ
|00+αα
|11+ββ
|10+α
β|01
34
) +
|0010(αα
|00−αβ
|11+α
β|10+ββ
|01
34
) +
|0011(αβ
|00−αα
|11+ββ
|10+α
β|01
34
) +
|0100(α
β|00+ββ
|11+αα
|10+αβ
|01
34
) +
|0101(ββ
|00+α
β|11+αβ
|10+αα
|01
34
) +
|0110(α
β|00−ββ
|11+αα
|10+αβ
|01
34
) +
|0111(ββ
|00−α
β|11+αβ
|10+αα
|01
34
)
+
|0000(αα
|00+αβ
|11−α
β|10−ββ
|01
34
) +
|0001(αβ
|00+αα
|11−ββ
|10−α
β|01
34
) +
|0010(αα
|00−αβ
|11−α
β|10+ββ
|01
34
) +
|0011(αβ
|00−αα
|11−ββ
|10+α
β|01
34
) +
|1100(−α
β|00−ββ
|11+αα
|10+αβ
|01
34
) +
|1101(−ββ
|00−α
β|11+αβ
|10+αα
|01
34
) +
|1110(−α
β|00+ββ
|11+αα
|10−αβ
|01
34
) +
|1111(−ββ
|00+α
β|11+αβ
|10−αα
|01
34
)
(P12)
(for clarity, I have divided the 16 lines into two groups, m = 0 and m = 1, appearing
within the two columns in brackets [], respectively).
The result in Eq. (P12) reveals the details of the 16 post-measurement states, which
have the form
|mnm
n
1256
|θ
34
=|mnm
n
1256
(w|00+x|11+y|10+z|01)
34
. (P13)

642 Appendix P
Thus, each measurement from Alice that yields |mnm
n
1256
results in a corresponding
system collapse on Bob’s two wires |θ
34
. Last but not least, we must show that the 16
collapsed states |θ
34
indeed correspond to the proposed circuit shown in Fig. P1, and
involve the gates X
n
, X
n
, Z
n
, Z
n
corresponding to the cbits m, n, m
, n
. Formally, the
circuit corresponds to a tensor operator U
mnm
n
effecting the transformation
U
mnm
n
|θ
34
=|ψ (P14)
and defined as:
U
mnm
n
= Z
m
4
Z
m
3
Z
m
4
X
n
3
X
n
4
X
n
3
. (P15)
We must show that after passing through these gates, the resulting qubit is |ψ =
C
43
|q
3
⊗|q
4
. Substituting |q
3
and |q
4
from Eq. (P2) into the definition of |ψ,we
obtain:
|ψ=C
43
|q
3
⊗|q
4
= C
43
(α|0+β|1)
3
⊗|α
|0+β
|1
4
= C
43
(αα
|00+αβ
|01+α
β|10+ββ
|11)
34
≡ (αα
|00+αβ
|11+α
β|10+ββ
|01)
34
.
(P16)
It is then easily verified that U
mnm
n
|θ
34
=|ψ for any of the 16 post-measurement
states:
U
mnm
n
|θ
34
= Z
0
4
Z
0
3
Z
0
4
X
0
3
X
0
4
X
0
3
(αα
|00+αβ
|11+α
β|10+ββ
|01)
34
= Z
0
4
Z
0
3
Z
0
4
X
0
3
X
1
4
X
1
3
(αβ
|00+αα
|11+ββ
|10+α
β|01)
34
= Z
0
4
Z
0
3
Z
1
4
X
0
3
X
0
4
X
0
3
(αα
|00−αβ
|11+α
β|10−ββ
|01)
34
= Z
0
4
Z
0
3
Z
1
4
X
0
3
X
1
4
X
1
3
(αβ
|00−αα
|11+ββ
|10−α
β|01)
34
= Z
0
4
Z
0
3
Z
0
4
X
1
3
X
0
4
X
0
3
(α
β|00+ββ
|11+αα
|10+αβ
|01)
34
= Z
0
4
Z
0
3
Z
0
4
X
1
3
X
1
4
X
1
3
(ββ
|00+α
β|11+αβ
|10+αα
|01)
34
= Z
0
4
Z
0
3
Z
1
4
X
1
3
X
0
4
X
0
3
(α
β|00−ββ
|11+αα
|10−αβ
|01)
34
= Z
0
4
Z
0
3
Z
1
4
X
1
3
X
1
4
X
1
3
(ββ
|00−α
β|11+αβ
|10−αα
|01)
34
= Z
1
4
Z
1
3
Z
0
4
X
0
3
X
0
4
X
0
3
(αα
|00+αβ
|11−α
β|10−ββ
|01)
34
= Z
1
4
Z
1
3
Z
0
4
X
0
3
X
1
4
X
1
3
(αβ
|00+αα
|11−ββ
|10−α
β|01)
34
= Z
1
4
Z
1
3
Z
1
4
X
0
3
X
0
4
X
0
3
(αα
|00−αβ
|11−α
β|10+ββ
|01)
34
= Z
1
4
Z
1
3
Z
1
4
X
0
3
X
1
4
X
1
3
(αβ
|00−αα
|11−ββ
|10+α
β|01)
34
= Z
1
4
Z
1
3
Z
0
4
X
1
3
X
0
4
X
0
3
(−α
β|00−ββ
|11+αα
|10+αβ
|01)
34
= Z
1
4
Z
1
3
Z
0
4
X
1
3
X
1
4
X
1
3
(−ββ
|00−α
β|11+αβ
|10+αα
|01)
34
= Z
1
4
Z
1
3
Z
1
4
X
1
3
X
0
4
X
0
3
(−α
β|00+ββ
|11+αα
|10−αβ
|01)
34
= Z
1
4
Z
1
3
Z
1
4
X
1
3
X
1
4
X
1
3
(−ββ
|00+α
β|11+αβ
|10−αα
|01)
34
=|ψ .
.
(P17)

Two-qubit teleportation 643
The first equality in Eq. (P17), corresponding to |mnm
n
=|0000 is immediately
established by comparison with Eq. (P16). All the other equalities can be verified
with the understanding that they hold within an occasional (unobservable) phase factor
e
iπ
=−1. As an illustration of the verification, consider, for instance, the last equality
in Eq. (P16), and apply the Pauli operators as defined:
U
mnm
n
|θ
34
= Z
1
4
Z
1
3
Z
1
4
X
1
3
X
1
4
X
1
3
(−ββ
|00+α
β|11+αβ
|10−αα
|01)
34
= Z
1
4
Z
1
3
Z
1
4
X
1
3
(−ββ
|11+α
β|00+αβ
|01−αα
|10)
34
= Z
1
4
Z
1
3
Z
1
4
(−ββ
|01+α
β|10+αβ
|11−αα
|00)
34
= Z
1
4
Z
1
3
(ββ
|01+α
β|10−αβ
|11−αα
|00)
34
= Z
1
4
(ββ
|01−α
β|10+αβ
|11−αα
|00)
34
= (−ββ
|01−α
β|10−αβ
|11−αα
|00)
34
=−(αα
|00+αβ
|11+α
β|10+ββ
|01)
34
≡ e
iπ
|ψ. (P18)
The operation of the quantum circuit, together with Alice transmitting her four measured
cbits m, n, m
, n
to Bob, thus, result in the successful teleportation of the tensor state
|ψ, as defined in Eq. (P16). As mentioned at the beginning of this appendix, Bob can
retrieve Alice’s qubits |q, |q
by effecting a final CNOT operation on |ψ , as described
by the operator C
34
. Indeed,
|ψ
out
=C
43
|ψ
= C
43
(αα
|00+αβ
|11+α
β|10+ββ
|01)
34
= (αα
|00+αβ
|01+α
β|10+ββ
|11)
34
= (α|0+β|1)
3
⊗|α
|0+β
|1
4
≡|q
3
⊗|q
4
,
(P19)
which shows that |ψ
is the unique tensor product of the qubits |q, |q
.

Appendix Q (Chapter 19) Quantum
Fourier transform circuit
In this appendix, I develop a simplified tensor-product expression for the components
resulting from the quantum Fourier transform (QFT) of N -qubits. This expression leads
to the conception of a corresponding QFT circuit based on simple 2 ×2 quantum gates.
The starting point is the fundamental QFT definition (Eq. (19.16)), which transforms
the orthonormal basis
|
n
according to
QFT
|
n
=
1
√
N
N −1
k=0
e
ik
2nπ
N
|k. (Q1)
The goal is to reduce the right-hand side in this expression into a tractable tensor product,
from which a simple QFT gate circuit can be constructed. I focus on the imaginary-
exponential terms in Eq. (Q1), namely exp(2
i
πkn/N ), where k, n = 0 ...N − 1. From
this point on, we assume that N is exactly a power of two, i.e., N = 2
K
, where K ≥ 1is
an integer. We now expand the integer k according to the possible binary representation
k ≡ k
1
2
K −1
+ k
2
2
K −2
+···+k
K
2
0
, where k
p
= 0, 1 and k = 1, 2 ...K , and express
the ratio k/N according to
k
N
=
k
2
K
= k
1
2
−1
+ k
2
2
−2
+···+k
K
2
−K
=
K
p=1
k
p
2
p
.
(Q2)
Substituting this representation into the exponential in Eq. (Q1), and introducing next
the tensor notation |k=|k
1
k
2
...k
K
we obtain
QFT|n=
1
2
K /2
2
K
−1
k=0
exp
2
i
πn
K
p=1
k
p
2
p
|k, (Q3)

Quantum Fourier transform circuit 645
QFT|n=
1
2
K /2
k
1
,k
2
,...,k
K
=0,1
exp
2
i
πn
K
p=1
k
p
2
p
|
k
1
k
2
...k
K
=
1
2
K /2
k
1
=0,1
k
2
=0,1
···
k
K
=0,1
exp
2
i
πn
K
p=1
k
p
2
p
|
k
1
k
2
...k
K
≡
1
2
K /2
k
1
=0,1
e
2
i
πn
k
1
2
1
|
k
1
⊗
k
2
=0,1
e
2
i
πn
k
2
2
2
|
k
2
⊗···⊗
k
K
=0,1
e
2
i
πn
k
K
2
K
|
k
K
.
(Q4)
This result shows that QFT
|
n
can be decomposed indeed into a K -tensor product. In
this decomposition, each term, indexed by p, is actually made of the two contributions:
k
p
=0,1
e
2
i
πn
k
p
2
p
|k
p
=
|
0
+
e
2
i
πn
2
p
|1. (Q5)
Hence, we can develop Eq. (Q5) according to:
QFT|n=
1
2
K /2
|0
1
+
e
2
i
πn
2
1
|1
1
⊗
|0
2
+
e
2
i
πn
2
2
|1
2
⊗···⊗
|0
K
+
e
2
i
πn
2
K
|1
K
.
(Q6)
The next step is to simplify further each of the exponential terms in Eq. (Q6). To do
this, we substitute the binary expansion for integers n, namely, n = n
1
2
K −1
+ n
2
2
K −2
+
···+n
K −1
2
1
+ n
K
2
0
, where n
q
= 0, 1, in each of the exponents, which gives
2
i
π
n
2
1
= 2
i
π
n
1
2
K −2
+ n
2
2
K −3
+···+n
K −1
+
n
K
2
1
2
i
π
n
2
2
= 2
i
π
n
1
2
K −3
+ n
2
2
K −4
+···+n
K −2
+
n
K −1
2
1
+ n
k
K
2
2
.
.
.
2
i
π
n
2
K −1
= 2
i
π
(
n
1
)
+
n
2
2
1
+···+
n
K −1
2
K −2
+
n
K
2
K −1
2
i
π
n
2
K
= 2
i
π
n
1
2
1
+
n
2
2
2
+···+
n
K −1
2
K −1
+
n
K
2
K
.
(Q7)
In the above, I have put in parentheses all the integer terms, to separate them from the
other terms that are defined as fractions of powers of two. Clearly, the integer terms do
not contribute to the imaginary exponential. The consequence of this can be generalized
under the formula
exp
#
2
i
π
n
2
m
$
= exp
(
2
i
π
m
)
m
=
m
l=1
n
K −m+l
2
l
.
(Q8)
646 Appendix Q
1
n
2
n
3
n
1
−
K
n
K
n
10
1
2
Ω
+
π
i
e
10
2
2
Ω
+
π
i
e
10
2
K
i
e
Ω
+
π
10
1
2
−
Ω
+
K
i
e
π
10
2
2
−
Ω
+
K
i
e
π
1
2
3
1−
K
K
1
2
3
1−
K
K
2−
K
n
10
3
2
Ω
+
π
i
e
2−
K
H
H
2
R
H
2
R
3
R
2−
K
Figure Q1 Gate circuit corresponding to first three output qubits.
From Eqs. (Q6)–(Q8), we finally obtain a nice closed-formed expression for the QFT
tensor product:
QFT|n=
1
2
K /2
|0
1
+
e
2
i
π
1
|1
1
⊗
|0
2
+
e
2
i
π
2
|1
2
⊗···⊗
|0
K
+
e
2
i
π
K
|1
K
.
(Q9)
With
|
n
=|n
1
n
2
...n
K
, we have the following relation for each of the gate outputs
QFT|n
p
=
1
2
K /2
|0
p
+
e
2
i
π
p
|1
p
. (Q9)
Considering the first output qubits we have
QFT|n
1
=
1
2
K /2
(|0
1
+
e
2
i
1
|1
1
)
=
1
2
K /2
(
|0
1
+
e
iπn
K
|1
1
)
,
(Q10)
which shows that (within the normalization factor 2
K /2
) the QFT circuit wire corresponds
either to the identity gate I (with input n
K
= 0) or the Hadamard gate H (with input n
K
=
1). We can then proceed to construct the QFT circuit from bottom to top, numbering
the output qubits from 1 to K, accordingly. As for the second output qubit, we have
2
i
π
2
=
i
π(n
K −1
+ n
K
/2) and then:
QFT|n
2
=
1
2
K /2
|0
2
+
e
2
i
2
|1
2
=
1
2
K /2
|0
2
+
e
iπn
K −1
e
i
π
2
n
K
|1
2
. (Q11)
We can immediately identify the above transformation as built from a Hadamard gate on
the output wire 2 with input n
K −1
, and a controlled-phase gate (call it R
2
), with phase
πn
K
/2 and n
K
as the control qubit. The next output qubit is
QFT|n
3
=
1
2
K /2
|0
3
+
e
2
i
3
|1
3
=
1
2
K /2
|0
3
+
e
iπn
K −2
e
i
π
2
n
K −1
e
i
π
4
n
K
|1
3
. (Q12)
