Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


Appendix K (Chapter 13) Capacity of
binary communication channels
In this appendix, I provide the solution of the maximization problem for mutual infor-
mation, which defines the channel capacity:
C = max
p(x)
H(X ; Y ), (K1)
as applicable to the general case of a binary communication channel (symmetric or
asymmetric), whose transition matrix is defined according to
P(Y |X) =
p(y
1
|x
1
) p(y
1
|x
2
)
p(y
2
|x
1
) p(y
2
|x
2
)
=
a 1 −b
1 − ab
,
(K2)
where a, b are real numbers in the interval [0, 1]. To recall, the channel mutual infor-
mation H (X; Y )isgivenby
H(X ; Y ) = H (Y ) − H(Y |X ). (K3)
Thus, we must first calculate the output-source entropy H (Y ) and the equivocation
entropy H (Y |X ). For this, we need the output probability distribution p(y
1
), p(y
2
),
which is obtained from the transition-matrix elements in Eq. (K2) as follows:
p(y
1
) = p(y
1
|x
1
)p(x
1
) + p(y
1
|x
2
)p(x
2
)
= aq +(1 −b)(1 −q)
p(y
2
) = p(y
2
|x
1
)p(x
1
) + p(y
2
|x
2
)p(x
2
)
= (1 −a)q + b(1 − q)
≡ 1 − p(y
1
).
(K4)
In Eq. (K4), we have defined the input probability distribution according to p(x
1
) = q
and p(x
2
) = 1 − q.FromEq.(K4), we can calculate the output-source entropy:
H(Y ) =−p(y
1
)logp(y
1
) − p(y
2
)logp(y
2
)
=−p(y
1
)logp(y
1
) − [1 − p(y
1
)] log[1 − p(y
1
)]
= f [ p(y
1
)]
= f [aq + (1 −b)(1 − q)],
(K5)

618 Appendix K
where the function f is defined by
f (u) = f (1 − u)
=−u log u − (1 −u)log(1− u),
(K6)
noting that, as usual, the logarithms are in base two.
The next step consists of calculating the equivocation H (Y |X ). For this, we need
the joint distribution p(x, y). Using Bayes’s theorem and the conditional probabilities
shown in Eq. (K2) we obtain:
p(y
1
, x
1
) = p(y
1
|x
1
)p(x
1
) = aq
p(y
1
, x
2
) = p(y
1
|x
2
)p(x
2
) = (1 − b)(1 − q)
p(y
2
, x
1
) = p(y
2
|x
1
)p(x
1
) = (1 − a)q
p(y
2
, x
2
) = p(y
2
|x
2
)p(x
2
) = b(1 −q).
(K7)
The results in Eq. (K5) now make it possible to calculate the equivocation H (Y |X):
H(Y |X ) =−
2
i=1
2
j=1
p(x
i
, y
j
)logp(y
j
|x
i
)
=−[aq log a + (1 −a)q log(1 − a)
+ (1 − b)(1 − q)log(1− b) +b(1 − q)logb]
≡ qf(a) +(1 −q) f (b).
(K8)
Substituting Eqs. (K7) and (K8)inEq.(K3), we obtain the mutual information H(X; Y ):
H(X ; Y ) = f [aq + (1 −b)(1 − q)] −qf(a) −(1 − q) f (b). (K9)
Setting q = 0orq = 1 in the result in Eq. (K9) yields, in both cases, H(X ; Y ) = 0. The
case a = 1 −b (or a + b = 1) corresponds to H(X ; Y ) = 0, as can easily be verified
from Eq. (K9). This means that, regardless of the input probability distribution, the
mutual information is zero. As discussed in the main text, such a channel is useless.
The condition a = 1 − b in the transition matrix (Eq. (K2)) represents the most general
definition of useless channels, i.e., including but not limited to the case a = b = ε = 1/2.
In the general case, we have H (X ; Y ) ≥ 0, and the function is concave (meaning that
a cord between any two points is always below the maximum). Therefore, the maximum
of H(X ; Y ) ≥ 0 is given by the root of the derivative dH(X ; Y )/
d
q. Thus, we must
solve
dH (X; Y )
dq
=
d
dq
{
f [aq + (1 −b)(1 − q)] −qf(a) − (1 −q) f (b)
}
= 0.
(K10)
Using the definition of f in Eq. (K8) and going through elementary calculations yields
the following solution for q:
q =
1
a + b − 1
b −1 +
1
1 + 2
W
, (K11)

Capacity of binary communication channels 619
with
W =
f (a) − f (b)
a + b − 1
. (K12)
Concerning the continuity of the above solution in the case a + b = 1, see the note at
the end of this appendix.
The optimal distribution defined in Eqs. (K11) and (K12) can now be substituted into
Eq. (K10). After elementary calculation, we obtain:
C = max
q
H(X ; Y )
= log(1 + 2
W
) − W
2
W
1 + 2
W
−q[ f (b) − f (a)] − f (b)
= log(1 + 2
W
) +
(1 − a) f (b) − bf(a)
a + b − 1
.
(K13)
Define
U =
(1 − a) f (b) − bf(a)
a + b − 1
(K14)
and substitute U in Eq. (K13) to get the channel capacity:
C = log(1 + 2
W
) + U
= log[(1 + 2
W
)2
U
]
= log(2
U
+ 2
U+W
)
≡ log(2
U
+ 2
V
),
(K15)
with
V = U + W =
(1 − b) f (a) − af(b)
a + b − 1
. (K16)
Note
The optimal probability distribution q = p(x
1
) = 1 − p(x
2
) defined in Eqs. (K11) and
(K12) seemingly has a pole in a + b = 1. I show herewith that it is actually defined over
the whole plane a, b ∈ [0, 1], namely, that it is analytically defined in the limiting case
a + b = 1. I shall establish this by first setting a + b = 1 −ε in Eq. (K11), then using
the Taylor expansion of the function f (a + ε) to the second order, i.e.,
f (a + ε) = f (a) + ε log
1 − a
a
+ ε
2
1
2a(1 −a)
,
which gives
W = log
1 − a
a
+ ε
1
2a(1 −a)
.
By substituting this result in Eq. (K11), and expanding the exponential term, one
easily finds 1/(1 + 2
W
) ≈ a − ε/2, which gives the limit q = 1/2, corresponding to

620 Appendix K
the uniform distribution. However, such a distribution does not maximize the mutual
information H (Y ; X), since we have seen that in the limiting case a + b = 1wehave
H(Y ; X) = 0.
I show next that the channel capacity is also defined over the plane a, b ∈ [0, 1],
including the limiting case a + b = 1. Indeed, using the same Taylor expansion as
previously, we easily obtain
U = (1 −a)log
a
1 − a
− f (a) +
ε
2a
= log a +
ε
2a
≈ log a.
Substituting this result and 1/(1 + 2
W
) ≈ a − ε/2 ≈ a into Eq. (K15) yields C =
log(1 +2
W
) + U ≈−log a + log a = 0, which is the expected channel capacity in the
limiting case a + b = 1. The function V is also found to take the limit V ≈ log(1 − a),
which, from Eq. (K15), also gives C = log(2
U
+ 2
V
) ≈ 0.

Appendix L (Chapter 13) Converse
proof of the channel coding theorem
This appendix provides the converse proof of the CCT.
1
The converse proof must show
that to achieve transmission with arbitrary level accuracy (or error probability), the
condition R ≤ C must be fulfilled. The demonstration seeks to establish two properties,
which I shall name A and B.
Property A
To begin with, we must establish the following property, referred to as Fano’s inequality,
according to which:
H(X
n
|Y
n
) ≤ 1 + p
e
nR, (L1)
where p
e
is the error probability of the code ( p
e
= 1 −
˜
p), i.e., the probability that the
code will output a codeword that is different from the input message codeword.
To demonstrate Fano’s inequality, we define W = 1 ...2
nR
as the integer that labels
the 2
nR
possible codewords in the input-message codebook. We can view the code
as generating an output integer label W
, to which the label W of the input message
codeword may or may not correspond. We can, thus, write p
e
= p(W
= W ). We then
define a binary random variable E, which tells whether or not a codeword error occurred:
E = 1, if W
= W , and E = 0, if W
= W .Thus,wehave p(E = 1) = p
e
and p(E =
0) = 1 − p
e
. We can then introduce the conditional entropy H (E, W |Y
n
), which is the
average information we have on E, W , given the knowledge of the output codeword
source, Y
n
. Referring back to the chain rule in Eqs. (5.22) and (5.23), we can expand
H(E, W |Y
n
) in two different ways:
H(E, W |Y
n
) = H (E|Y
n
) + H (W |E , Y
n
)
= H (W |Y
n
) + H (E |W, Y
n
).
(L2)
Since E is given by the combined knowledge of label W and output source Y
n
,we
have H (E|W, Y
n
) = 0. We also have H (E|Y
n
) = H (E), since the only knowledge of
Y
n
does not condition the knowledge of E. Substituting these results into Eq. (L2), we
1
Inspired from M. Cover and J. A. Thomas, Elements of Information Theory (New York: John Wiley & Sons,
1991), pp. 203–9.

622 Appendix L
obtain
H(W |Y
n
) = H (E) + H(W |E, Y
n
). (L3)
We shall now find an upper bound for H (W |Y
n
). First, we can decompose the second
term in the right-hand side in Eq. (L3)asfollows:
H(W |E, Y
n
) = p(E = 0)H(W |Y
n
, E = 0) + p(E = 1)H(W |Y
n
, E = 1)
= (1 − p
e
)H (W |Y
n
, E = 0) + p
e
H(W |Y
n
, E = 1).
(L4)
We have H(W |Y
n
, E = 0) = 0, since knowing Y
n
and that there is no codeword error is
equivalent to knowing the input codeword label W . Second, we have H(W |Y
n
, E = 1) ≤
log(2
nR
− 1) < log(2
nR
) = nR, since knowing Y
n
and that there is a codeword error,
the number of mistaken codeword possibilities is 2
nR
− 1, with uniform probability
q = 1/(2
nR
− 1); hence the entropy can be upper bounded by H
=−log(q) < nR.
Finally, we have H (E) ≤ 1, since E is a binary random variable. Substituting the two
upper bounds into Eq. (L3) yields:
H(W |Y
n
) ≤ 1 + p
e
nR (L4)
and
H(X
n
|Y
n
) ≤ 1 + p
e
nR, (L5)
since the knowledge of the input message source X
n
and the codeword label W are
equivalent. Equation (L5) is Fano’s inequality.
Property B
The second tool required for the converse proof of the CCT is the property according
to which the channel capacity per transmission is not increased by passing through
the data several times. Note that this property is true if one assumes that the channel
is memoryless, namely that there is no possible correlation between errors concerning
successive bits or successive codewords.
As I established earlier, the channel capacity for an n-bit codeword is nC, where C
is the capacity of the binary channel, corresponding to a single bit transmission. The
proposed new property can be restated as
H(X
n
; Y
n
) ≤ nC. (L6)
The corresponding proof of Eq. (L6) is relatively straightforward. Indeed, we have, by
definition
H(X
n
; Y
n
) = H (Y
n
) − H (Y
n
|X
n
). (L7)

Converse proof of the channel coding theorem 623
Let us now develop the second term in the right-hand side in Eq. (L7)asfollows:
H(Y
n
|X
n
) = H(y
1
|X
n
) + H (y
2
|y
1
, X
n
) +···+H(y
n
|y
1
, y
2
,...,y
n−1
, X
n
)
=
n
i=1
H(y
i
|y
1
, y
2
,...y
i−1
, X
n
)
=
n
i=1
H(y
i
|x
i
).
(L8)
The first equality stems from substituting the extended output source Y
n
= y
1
, Y
n−1
,
Y
n−1
= y
2
, Y
n−2
, etc., (here y
k
means the binary source of bit or rank k in the codeword),
into the chain rule (Eq. (5.22)) as follows:
H(Y
n
|X
n
) ≡ H(y
1
, Y
n−1
|X
n
)
= H (y
1
|X
n
) + H (Y
n−1
|y
1
, X
n
)
= H (y
1
|X
n
) + H (y
2
Y
n−2
|y
1
, X
n
)
= H (y
1
|X
n
) + H (y
2
|y
1
, X
n
) + H (Y
n−2
|y
1
, y
2
, X
n
)
=···
≡ H (y
1
|X
n
) + H (y
2
|y
1
, X
n
) +···+H(y
n
|y
1
, y
2
,...,y
n−1
, X
n
).
(L9)
The last equality in Eq. (L8) stems from the fact that, assuming a memoryless chan-
nel, all received bits y
1
, y
2
,...,y
i−1
are uncorrelated with the received bit y
i
, hence
H(y
i
|y
1
, y
2
,...,y
i−1
, X
n
) = H (y
i
|X
n
). Furthermore, the knowledge of y
i
is not con-
ditioned to that of the input message bits x
1
, x
2
,...,x
n
except for the bit x
i
of the same
rank i in the codeword, hence H(y
i
|y
1
, y
2
,...,y
i−1
, X
n
) = H (y
i
|x
i
). Substituting the
result in Eq. (L8) into Eq. (L7) yields:
H(X
n
; Y
n
) = H (Y
n
) −
n
i=1
H(y
i
|x
i
). (L10)
Next, we look for an upper bound in the right-hand side in Eq. (L8). We observe that
H(Y
n
) ≤
n
i=1
H(y
i
), the equality standing if the distribution p(y
i
) was uniform, in
which case we would have H(y
i
) ≡ H (Y ) and H(Y
n
) = nH(Y ). Applying the inequality
to Eq. (L10) we finally obtain
H(X
n
; Y
n
) ≤
n
i=1
H(y
i
) −
n
i=1
H(y
i
|x
i
)
=
n
i=1
[
H(y
i
) − H (y
i
|x
i
)
]
≡
n
i=1
H(x
i
; y
i
).
(L11)
This result shows that the mutual information between the two transmitted or received
codeword sources is less than or equal to the sum of mutual information between the
transmitted or received bits in the binary channel. Since, by definition, H(x
i
; y
i
) ≤

624 Appendix L
max H(x
i
; y
i
) = C, where C is the binary-channel capacity, we also have
H(X
n
; Y
n
) ≤ nC. (L12)
This result establishes that the mutual information between extended sources X
n
, Y
n
,
where bits are passed through the channel n times, is no greater than n times the binary-
channel capacity.
The two properties A and B can now be used (finally!) to establish the converse proof
of the CCT. As before, we assume that the 2
nR
input message codewords are chosen at
random with a uniform distribution, hence H (X
n
) = nR. By definition of the mutual
information, H (X
n
; Y
n
), and introducing the majoring properties A and B, we obtain
H(X
n
; Y
n
) = H (X
n
) − H (X
n
|Y
n
)
↔
nR = H (X
n
) = H (X
n
; Y
n
) + H (X
n
|Y
n
)
nR ≤ nC +1 + p
e
nR
↔
R ≤ p
e
R +
1
n
+ C.
(L13)
Since the starting assumption is that the error probability of the code, p
e
, vanishes for
n →∞, the above result asymptotically becomes:
R ≤ C, (L14)
which represents a necessary condition and, hence, proves the converse of the CCT.
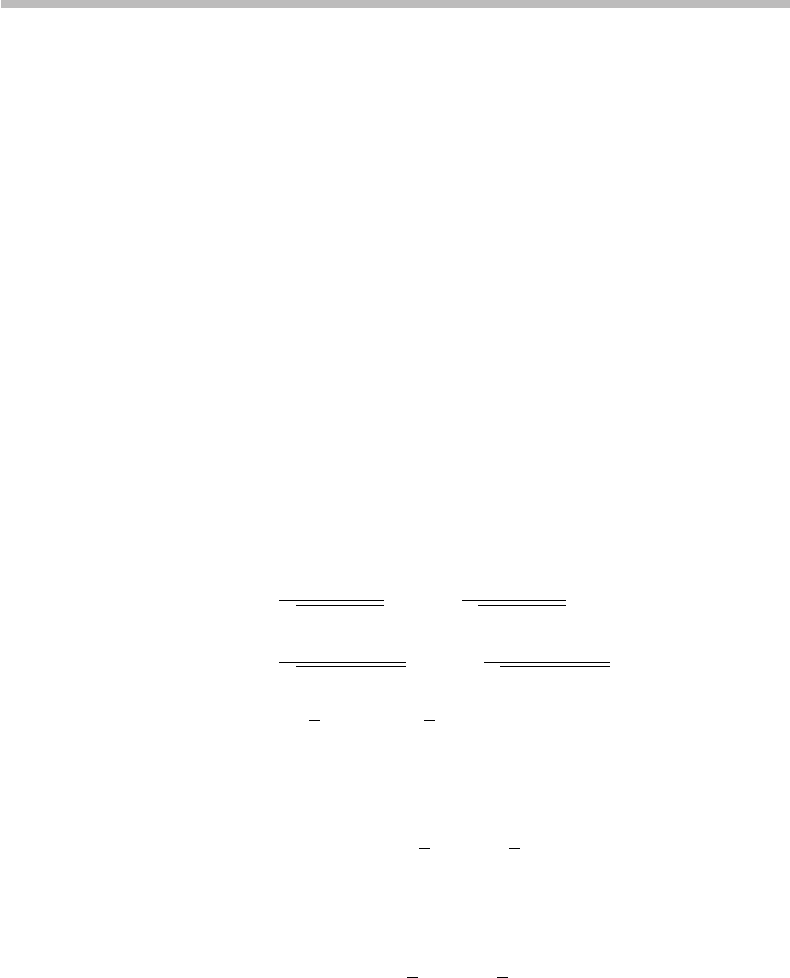
Appendix M (Chapter 16) Bloch sphere
representation of the qubit
In this appendix, I show that qubits can be represented by a unique point on the surface
of a sphere, referred to as a Bloch sphere.
As seen from the main text, any qubit can be represented as the vector linear super-
position
|q=α|0+β|1, (M1)
where |0, |1 form an orthonormal basis in the 2D vector space, and α, β are complex
numbers, which represent the qubit coordinates in this space. The length of the qubit
vector |q is, therefore, given by |α|
2
+|β|
2
. Since any two complex numbers α, β
can be defined in the exponential representation as α =|a|e
i
θ
1
and β =|β|
e
i
θ
2
, one can
write, from Eq. (M1):
|q=α|0+β|1=|a|
e
i
θ
1
|0+|β|
e
i
θ
2
|1 (M2)
Assume next that the qubit vector is unitary, i.e., |α|
2
+|β|
2
= 1. Substituting this
property and with the definition tan(θ/2) =|β|/|α|, we obtain from Eq. (M2):
|q=
|α|
|α|
2
+|β|
2
e
i
θ
1
|0+
|β|
|α|
2
+|β|
2
e
i
θ
2
|1
=
1
1 + tan
2
(θ/2)
e
i
θ
1
|0+
tan
2
(θ/2)
1 + tan
2
(θ/2)
e
i
θ
2
|1
≡ cos
θ
2
e
i
θ
1
|0+sin
θ
2
e
i
θ
2
|1,
(M3)
with 0 ≤ θ ≤ π/2.
Finally, introducing γ = θ
1
and ϕ = θ
2
− θ
1
, the qubit takes the form
|q=
e
i
γ
cos
θ
2
|0+sin
θ
2
e
i
ϕ
|1
. (M4)
Overlooking the argument γ , which only represents an arbitrary (said “unobservable”)
phase shift, we finally obtain
|q=cos
θ
2
|0+sin
θ
2
e
iϕ
|1. (M5)

626 Appendix M
0
1
θ
q
ϕ
x
y
z
Figure M1 Qubit represented as point of coordinates (θ,ϕ) on Bloch sphere.
The qubit can, thus, be represented through two angular coordinates θ,ϕ, which define
the unique position of a point on a sphere of unit radius, which is the Bloch sphere
illustrated in Fig. M1.
It is seen from Fig. M1 that the pure qubits |0 or |1 correspond to θ = 0orθ = π,
respectively, which occupy the north and south poles of the Bloch sphere. The qubit
representation of quantum information, thus, corresponds to an infinity of states located
on the surface of the Bloch sphere. See more on this topic in Appendix N.
