Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

Quantum Fourier transform circuit 647

We can immediately identify the above transformation as built from a Hadamard gate

on the output wire 3 with input n

K −2

, the controlled-phase gate R

, with n

K −1

as the

control qubit, followed by a second gate (call it R

), with phase π n

/4 and n

as the

control qubit.

The gate circuit corresponding to the ﬁrst three output qubits is illustrated in Fig. Q1.

It is clear from the above description and the deﬁnition of 

in Eq. (Q8) that the whole

QFT circuit represents a generalization of that shown in Fig. Q1, with a sequence of

controlled-phase gates deﬁned by the matrix

. (Q13)

On the top quantum wire, the gate sequence from left to right is thus: HR

...R

(see Fig. 19.4 in main text for a complete view of the QFT circuit).

Appendix R (Chapter 20) Properties of

continued fraction expansion

This appendix provides the proof of three key properties of the continued fraction

expansion.

First, deﬁne the real number x

through a suite of positive real numbers [a

, a

,...,a

]

according to the continued fraction

= a

+···

, (R1)

with n ≤ N . Each real number in the set

{

, x

,...,x

N −1

, x

}

is called a convergent

of x

, while x

is called the nth convergent of x

Property 1

The ﬁnite suite

[

, a

,...,a

]

of positive real numbers corresponds to the ratio x

, as deﬁned through:



= a

n−1

+ p

n−2

= a

n−1

n−2

(R2)

with n ≥ 2, p

= a

, q

= 1, p

= 1 +a

, and q

= a

for n = 0, 1.

The proof of these relations comes by induction. Indeed, for n = 0, 1, we have:



= a

= 1

→

≡ a

, (R3)



= 1 + a

= a

→

1 + a

≡ a

. (R4)

We then observe that:











= a

(R5)

Properties of continued fraction expansion 649

which illustrates that

[

, a

]

and

[

, a

+ 1/a

]

correspond to x

and x

, which

are the 2nd and the 3rd convergents of x

, respectively. Assume next that the relations in

Eq. (R2) apply to any order n ≥ 1. We must then show that the relations also apply to the

order n + 1. Then given the nth convergent x

, i.e.,

[

, a

,...,a

n−1

, a

]

,the(n + 1)th

convergent x

n+1

is of the form

[

, a

,...,a

n−1

, a

+ 1/a

n+1

]

. Applying Eq. (R2),to

the latter, we obtain

n+1



n+1



n−1

+ p

n−2



n+1



n−1

n−2

. (R6)

Multiplying the numerator and denominator in Eq. (R6) by a

n+1

and reordering terms

yields

n+1

(

n−1

+ p

n−2

)

+ p

n−1

n+1

(

n−1

n−2

)

n−1

n+1

+ p

n−1

n+1

n−1

≡

n+1

= x

n+1

(R7)

The result in Eq. (R7) shows that

n+1

= x

n+1

, corresponding to the suite

[

, a

,...,a

n+1

]

, which proves that the relations in Eq. (R2) apply at order

n + 1.

If the suite

[

, a

,...,a

]

is made of positive integers, then p

, q

are also positive

integers and x

= p

is a rational number for 0 ≤ n ≤ N .

Property 2

The real numbers p

, q

deﬁned in Eq. (R2) are co-prime, and satisfy the relation

(n ≥ 1):

n−1

− p

n−1

= (−1)

. (R8)

It is left as an easy exercise ﬁrst to prove the above by induction. Next, we must

show that p

, q

are co-prime, meaning that their greatest common divisor (GCD) is

one.

Assume that k ≥ 1 is some common divisor of p

, q

, i.e., p

= k

and q

= k

with p

. Likewise, assume that k



≥ 1 is some common divisor of

n−1

, q

n−1

, i.e., p

n−1

= k



n−1

and q

n−1

= k



n−1

, with p

n−1

. Sub-

stituting these deﬁnitions into Eq. (R8) yields:



(

n−1

−

n−1

)

= (−1)

. (R9)

650 Appendix R

Clearly,

has the same continued fraction expansion as p

at all orders n ≥ 1,

meaning that from Eq. (R8) we also have

n−1

−

n−1

= (−1)

and, hence, from

Eq. (R9):



= 1. (R10)

Consider next the case n = 1. Since q

= 1, we have k



= 1 (hence p

, q

are co-prime)

and from Eq. (R10),wehavek = 1 (hence p

, q

are co-prime). The same conclusion

applies to the case n = 2(p

, q

are co-prime, since p

, q

are co-prime), and so on,

which proves Property 2, according to which p

, q

are co-prime at all orders n ≥ 1.

Property 3

Given a rational number x, if two integers p, q are such that

− x

≤

, (R11)

then p/q is a convergent of x.

We can prove this property as follows. First, we know from the above description

that there exists a ﬁnite fraction expansion of the rational number x, as deﬁned by the

convergents x

= p

(n = 0, 1,...,N ). We shall assume, without loss of generality,

that n is even. We then deﬁne the error 0 ≤ δ ≤ 1 corresponding to the convergent x

according to

x −

. (R12)

We introduce

λ = 2

n−1

− p

n−1

−

n−1

, (R13)

for which (according to Eq. (R13))wehave

x =

λp

+ p

n−1

λq

n−1

. (R14)

The result in Eq. (R14) shows that λ = a

n+1

in the continued fraction expansion

, a

,...,a

,λ] that exactly deﬁnes x. Applying Property 2 in Eq. (R13), with n

being even, we obtain

λ =

−

n−1

>2−

n−1

(R15)

Since by deﬁnition q

n−1

is a rational number and also q

n−1

< 1, the result in

Eq. (R15) implies that λ>1, and also that λ is a rational number. Consequently, λ can

be exactly expressed through a ﬁnite, continued fraction expansion

[

, b

,...,b

]

, and,

Properties of continued fraction expansion 651

thus, the fraction expansion

[

, a

,...,a

, b

,...,b

]

exactly deﬁnes x.Thekey

conclusion is that the condition in Eq. (R9) is necessary and sufﬁcient for any rational

number p/q to be convergent on x.

I shall now illustrate Property 3 through a numerical example, which links to the

problem to be solved in the main text. As described in the text, the phase measurement

circuit yields the value x = ˜ϕ, which is a fair approximation of the exact phase ϕ = p/q,

where p, q are integers. The problem is that given x, we must ﬁnd the exact integer q.

Assume, for instance, that the exact phase ϕ = p/q is

ϕ =

711

413

≡ 1.72154963680387,

of which we obtain the following measurement value, and which we know (by choice of

the register size) to be accurate to 10

−6

˜ϕ = 1.721549(...).

Our task is now to obtain the exact value q = 413 by implementing the continuous

fraction expansion algorithm for the measurement ˜ϕ. For reference purposes, let us

expand ϕ ﬁrst. It is straightforward to obtain:

ϕ =

711

413

= 1 +

1 +

2 +

1 +

2 +

4 +

which shows that the suite

[

1, 1, 2, 1, 1, 2, 4, 5

]

is the expansion of ϕ.Weshallnow

expand ˜ϕ step by step, being careful to effect no truncation in the successive results. For

the ﬁrst three steps, we obtain

˜ϕ = 1.721549

= 1 +0.721549

= 1 +

0.721549

= 1 +

1.385907263401380

More precisely, the corresponding accuracy is ε =|ϕ − ˜ϕ|=3.69901547059293 × 10

−7

, representing in

the binary system (to be actually used for the algorithm implementation), an accuracy of up to 10 bits, since

−11

= 1.2 × 10

−7

<ε<2

−10

= 5.4 × 10

−7

652 Appendix R

Table R1 “Split and divide” expansion up to 12 steps.

= 1/

n−1

−a

n−1

) p

 1/2q

1/2q

−  Valid

0 1 1.721549000000000 1 1 1.00000000000000 7.215×10

−1

5.00×10

−1

−2.215×10

−1

1 1 1.385907263401380 2 1 2.00000000000000 2.785×10

−1

5.00×10

−1

2.215×10

−1

Ye s

2 2 2.591296134687970 5 3 1.66666666666667 5.488×10

−2

5.56×10

−2

6.726×10

−4

Ye s

3 1 1.691199961128960 7 4 1.75000000000000 2.845×10

−2

3.13×10

−2

2.800×10

−3

Ye s

4 1 1.446759340620720 12 7 1.71428571428571 7.264×10

−3

1.02×10

−2

2.940×10

−3

Ye s

5 2 2.238341561276870 31 18 1.72222222222222 6.726×10

−4

1.54×10

−3

8.706×10

−4

Ye s

6 4 4.195659349727770 136 79 1.72151898734177 3.065×10

−5

8.01×10

−5

4.947×10

−5

Ye s

7 5 5.110923660900250 711 413 1.72154963680387 0.000×10

2.93×10

−6

2.931×10

−6

Ye s

8 9 9.015209125664090 6535 3796 1.72154899894626 6.379×10

−7

3.47×10

−8

−6.032×10

−7

9 65 65.749999183803000 425486 247153 1.72154900001214 6.368×10

−7

8.19×10

−12

−6.368×10

−7

10 1 1.333334784351880 432021 250949 1.72154899999602 6.368×10

−7

7.94×10

−12

−6.368×10

−7

11 2 2.999986940889930 1289528 749051 1.72154900000133 6.368×10

−7

8.91×10

−13

−6.368×10

−7

= 1 +

1 + 0.385907263401380

= 1 +

1 +

0.385907263401380

= 1 +

1 +

2.591296134687970

= 1 +

1 +

2 + 0.591296134687970

= ...

The results of this “split and divide” expansion up to 12 steps are summarized in

Table R1. For each step n, the table lists the expansion coefﬁcient a

=u

, the ratio

= 1/(u

n−1

− a

n−1

), starting from u

= x, the integer numbers p

, q

as deﬁned

by Eq. (R2), the ratio p

, the error  =|p

− ϕ|, the upper bound 1/2q

Eq. (R11), and the difference 1/2q

− . If this difference is negative, this means that

the condition in Eq. (R11) is not valid, and hence that p

is not convergent on ϕ.We

observe from Table R1 that for n ≥ 1 the condition is valid up to the order n = 7, which

yields six convergents. The last convergent, p

= 711/413, is the exact deﬁnition

of ϕ. The algorithm has, thus, made it possible to determine ϕ = p/q unambiguously

given the approximation ˜ϕ and its known accuracy.

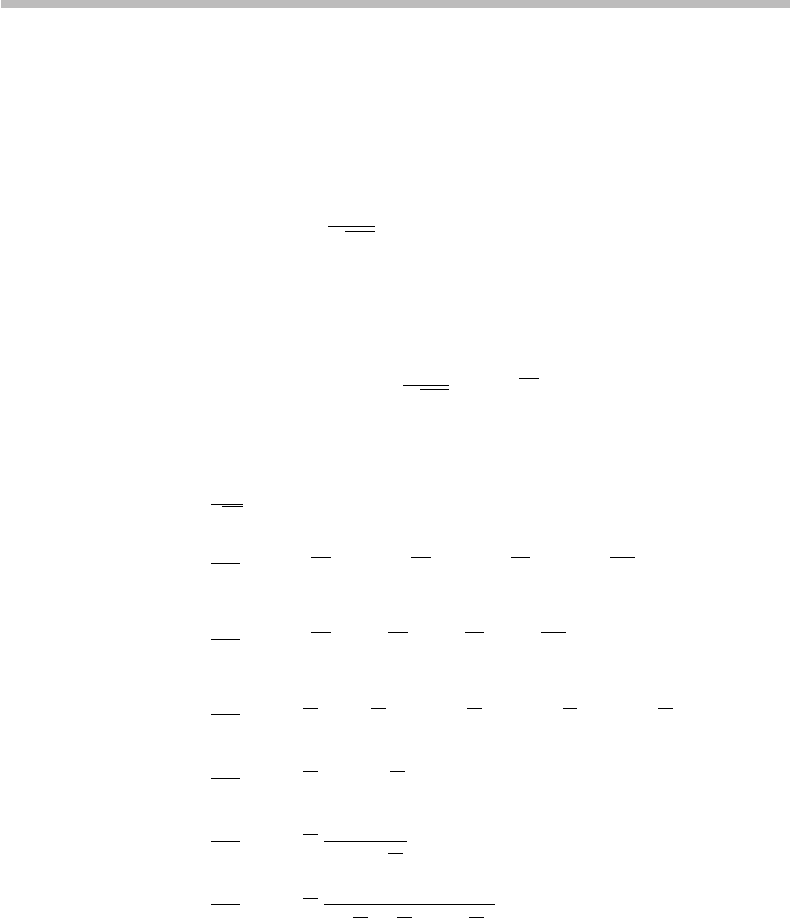
Appendix S (Chapter 20) Computation

of inverse Fourier transform in the

factorization of N = 21 through

Shor’s algorithm

In this appendix, I detail the computation of the inverse Fourier transform involved

in the factoring of N = 15 through Shor’s algorithm. To recall the parameters used in

Section 20.5, we have K = 11 for the ﬁrst register size and, thus, M = 2

= 2048.

After a measurement in the second register (z = 8), the state |u

 of the ﬁrst register,

which is input to the inverse Fourier transform circuit, is

=

√

(|1+|5+|9+|13+···). (S1)

By deﬁnition (see Chapter 19) the inverse Fourier transform FT

acts on the M-qubit

state |n according to

|n=

√

M−1



k=0

−k

πn

|k. (S2)

Thus, from the above deﬁnition of |u

, we obtain and develop the transformation as:

=

√

(|1+|5+|9+|13+···)

M−1



k=0



−k

π1

|k+

−k

π5

|k+

−k

π9

|k+

−k

π13

|k+···



M−1



k=0



−k

π1

−k

π5

−k

π9

−k

π13

+···



|k

M−1



k=0

−k





−k





−k





−k





−k



+···



|k

M−1



k=0

−k

M−1



m=0



−k



|k

≡

M−1



k=0

−k

1 −

−8

πk

1 −

−k

|k

M−1



k=0

−k

1 −

−8

πk

−k



−

−k



|k

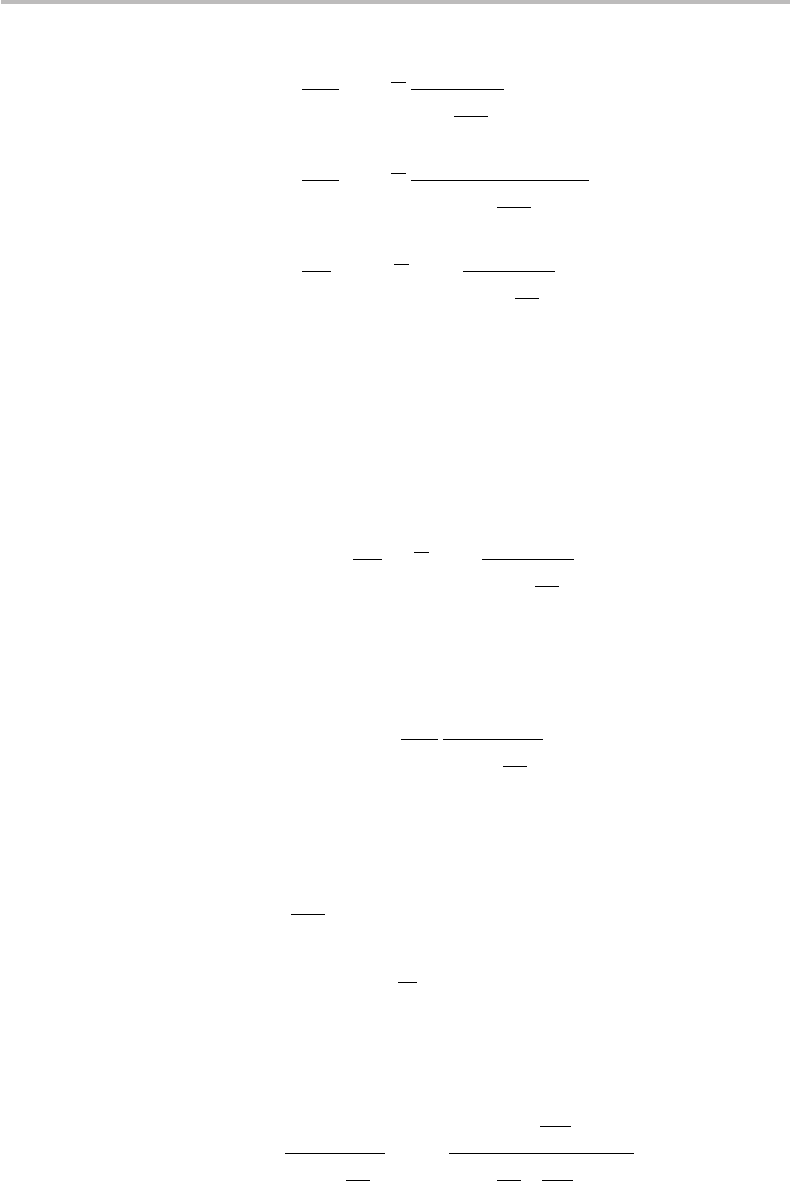
654 Appendix S

≡

4iM

M−1



k=0

1 −

−8

πk

sin



4πk



|k

4iM

M−1



k=0

−4

πk



πk

−

−4

πk



sin



4πk



|k

≡

M−1



k=0

−k

(2M−1)

sin(4πk)

sin



4π



|k. (S3)

We can rewrite the result in Eq. (S3)intheform

=

M−1



k=0

|k, (S4)

where the amplitude coefﬁcient α

is deﬁned by

−k

(2M−1)

sin(4πk)

sin



4π



. (S5)

The corresponding probability distribution p(k) =|α

corresponding to the output

measurement k is, therefore:

p(k) =

sin

(4πk)

sin



4π



. (S6)

We observe that for any integer k = 0, 1,...,M − 1, the numerator in Eq. (S6) is zero.

So is the denominator whenever 4πk/M is an integer multiple of π,or

4πk

= n × π

↔

k = n ×

= n × 2

= n × 512,

(S7)

where n is an integer. In this last case, the numerator: denominator ratio is analytically

undetermined, but setting k = nM/4 + ε and taking the limit:

lim

ε→0

sin

(4πk)

sin



4π



= lim

ε→0

sin



4π



+ ε



sin



4π



+ ε



Factorization of

= 21 through Shor’s algorithm 655

512

1024

1536

=2048

12047 −=

(

)

25.0

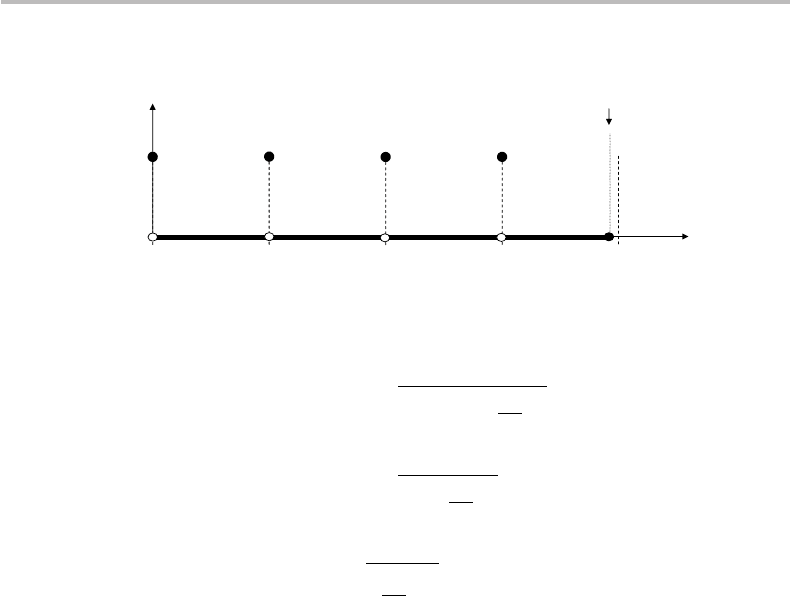
Figure S1 Plot of p(k).

= lim

ε→0

sin

(nMπ + 4πε)

sin



nπ +

4π



= lim

ε→0

sin

(4πε)

sin



4π



(4πε)



4π



≡ M

(S8)

which, from Eq. (S6), yields p

max

= 1/4. In the range k = 0, 1, 2,...,M − 1, the

maxima of p(k) are thus located at k = 0(n = 0), k = 512 (n = 1), k = 1024 (n = 2)

and k = 1536 (n = 3). The plot of p(k)isshowninFig. S1.

Appendix T (Chapter 20) Modular

arithmetic and Euler’s theorem

In this appendix, we shall review some basic principles and properties of modular

arithmetic. As Section 20.7 shows, modular arithmetic is at the root of public key

cryptography (PKC).

Let m and x be two integers, with m being nonzero. Deﬁne [x/m] as the integer part

of the division of x by m. If we consider, for instance, m = 3 and the ratios 2/3 = 0.66,

4/3 = 1.33, 6/3 =2 and 11/3 = 3.66, we, thus, obtain [2/3] = 0, [4/3] = 1, [6/3] = 2,

and [11/3] = 3. It is then possible to express any integer number x in the form:

x = m[x/m] +r, (T1)

where r stands for residue. With the previous examples, we have:











2 = 3[2/3] + 2

4 = 3[4/3] + 1

6 = 3[6/3] + 0

11 = 3[11/3] + 2.

(T2)

We observe that the residues are positive integers that range from r = 0tor = m − 1.

We can deﬁne such residues in the form

r = x − m[x/m]. (T3)

By convention, one designates the residues according to any of the following equivalent

notations:











r =|x|

r = x mod m

x ≡ r [m]

x = r (mod m),

(T4)

which reads as, “r equals x modulo m,” or “x equals r modulo m,” it being understood

which one is the residue. Here, we shall mainly use the second deﬁnition, with the

convention that “mod m” carries over the entire right-hand side expression or even

the full line (this to avoid a parenthesis inﬂation, unless parentheses are introduced