Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

15.3 Reversible logic gates and computation 297

way, without heat dissipation or entropy increase. The corresponding computer should

exclusively use reversible gates, which we shall analyze next.

15.3 Reversible logic gates and computation

In this section, I shall describe a new class of logic gates, which make it possible to build

a variety of reversible-computing circuits. The ﬁrst two elementary gates having such a

property are called the Fredkin and the Toffoli gates, which we shall consider now.

The Fredkin gate is illustrated in Fig. 15.7, along with its truth table. It is seen from

the ﬁgure that the Fredkin gate has three input ports (a, b, c) and three output ports



, b



, c



). Two input ports are used for the operand data (a, b), the third port being used

for a control bit (c). The gate operates according to the following logic (see also the

Figure’s truth table):

If c = 0, then a, b remain unchanged (a



= a, b



= b);

If c = 1, then a, b are swapped (a



= b, b



= a);

The control bit c remains unchanged (c



= c).

Figure 15.8(a) and (b) illustrate the ﬁrst two basic operations of the Fredkin gate:

REPEAT (c = 0) and CROSSOVER or SWAP (c = 1). But the gate can be conﬁgured

to perform other functions of interest, as shown in Fig. 15.8(c) and (d): setting a =

1, b = 0, c = x yields a



x (NOT x) and b



= c



= x (FANOUT x). Setting a =

0, b = y, c = x yields a



= x ∧ y (x AND y) and b



x ∧ y (

x AND y). The input

bits a, b, which are preset to constant values 0 or 1 in the Fredkin gate, as shown in

Fig. 15.8(c) and (d), are referred to as ancilla bits. Such ancilla bits, which are the key

to the operation of reversible gates, represent a novel concept in computational logic.

Another novelty is that reversible gates produce extra or garbage bits, which are not

useful to the rest of the computation (e.g., the bit b



x ∧ y in Fig. 15.8(d). Last but

not least, we notice from the Fredkin gate truth table (Fig. 15.7) that each output port

conﬁguration (a



, b



, c



) exclusively corresponds to a unique input port conﬁguration

(a, b, c). Thus, there exists a mutual and unique correspondence between the input and

the output information, hence, computation through the Fredkin gate is reversible.

Because the Fredkin gate can perform both NOT and AND logical functions, it can

be used as a universal building block to construct any other logic gate. To prove this

point, we need to introduce De Morgan’s law (or theorem).

Such a theorem can be put

in the form of the following equations:

a ∨ b =

a ∧

a ∧ b =

a ∨

(15.4)

In ensemble theory, De Morgan’s law equivalently translates into the relations

A ∪ B =

A ∩

B and

A ∩ B =

A ∪

B, which can be readily veriﬁed from Venn diagrams (see

Fig. 1.4). Using Eq. (15.4) we observe that the OR function can be generated through

See http://en.wikipedia.org/wiki/De_Morgan%27s_laws.

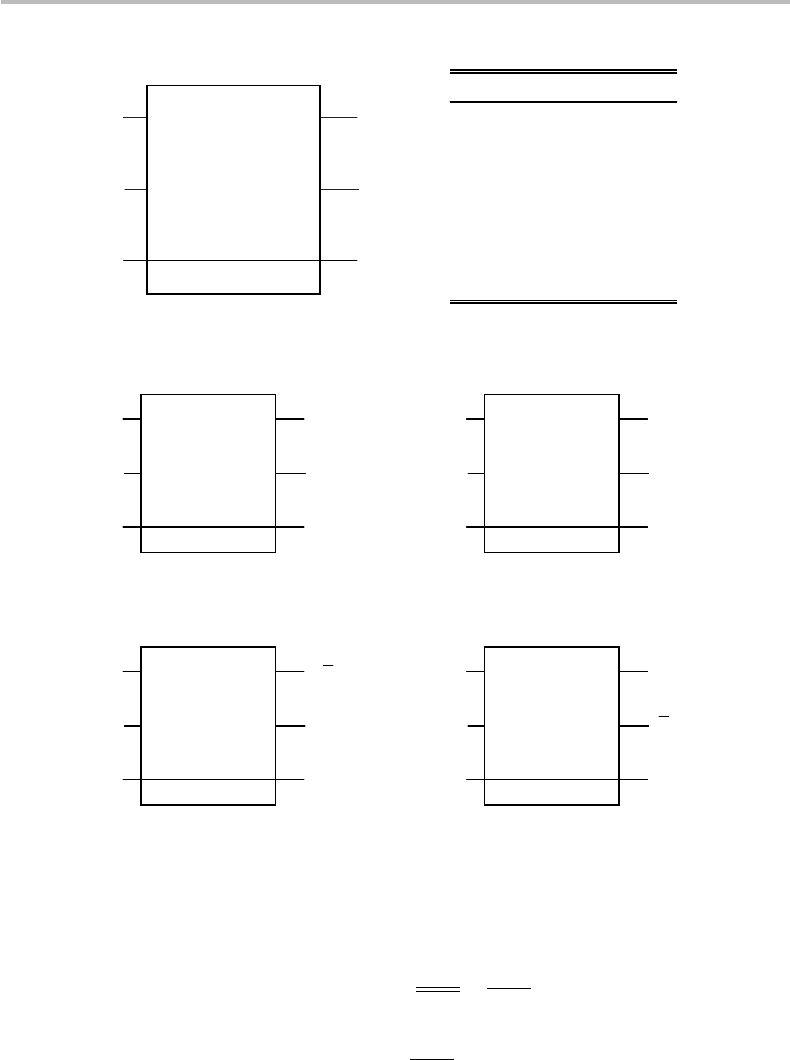
298 Reversible computation

abca

110110

100100

010010

000000

111111

101011

011101

001001

Figure 15.7 Fredkin gate diagram, with corresponding truth table.

(a) (b)

Figure 15.8 Fredkin gate conﬁgurations (a) REPEAT, (b) CROSSOVER, (c) NOT [port a



]and

FANOUT [ports b



and c



], (d) AND [port a



]andNOTx AND y [port b



the identity

a ∨ b =

a ∧

b, (15.5)

which exclusively uses the NOT and AND gates. Using the above property and the

relations in Eq. (15.1) (with a

∧ b =

a ∧ b), we observe that the function XOR can

be constructed either with NOT and AND gates or with NOT, AND, and OR gates.

Here, the key difference with the previous “classical” logic of the ALU in the VN

It is left as an exercise to construct different possibilities of XOR circuits exclusively based on Fredkin

gates.

15.3 Reversible logic gates and computation 299

´ =

a b c a´ b´ c´

000000

001001

010010

011011

100100

101101

110111

111110

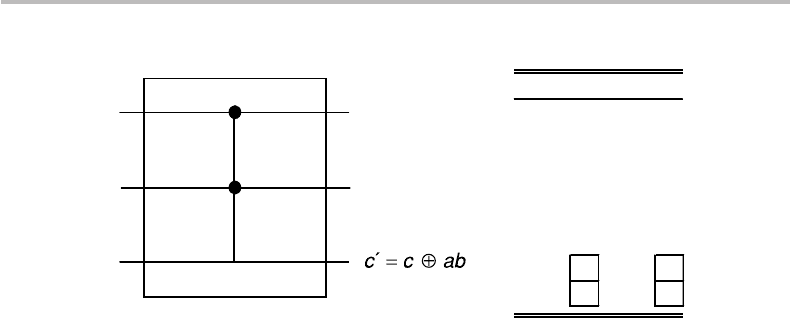
Figure 15.9 Toffoli gate diagram, with corresponding truth table, showing bit-ﬂipping of c if the

two control bits are set to a = b = 1.

computer is that all gate circuits constructed from Fredkin gates perform fully reversible

computations, by virtue of the gate’s reversible logic.

We consider next a second type of elementary reversible-logic gate, which is called

the Toffoli gate. Its diagram and corresponding truth table are shown in Fig. 15.9.Like

the Fredkin gate, the Toffoli gate has three input ports (a, b, c) and three output ports



, b



, c



). The difference is that a, b are control bits (a



= a, b



= b) and c is the target

bit. By convention, control bits are marked with a dot (•) and the target bit with a cross

(×). The Toffoli gate outputs c



= c ⊕(a ∧ b), or c



= c ⊕ab for short. The truth table

in the ﬁgure shows that the value of c is ﬂipped (function NOT) when the two control bits

are set to a = b = 1, and is left unchanged otherwise (function REPEAT). The Toffoli

gate can, thus, be conceived as a controlled-controlled-NOT (CCNOT) gate. As we shall

see next, the inputs (a, b, c) can also play different roles of variable, control, or ancilla

bits, with c



remaining the gate’s functional output bit, by deﬁnition.

Figure 15.10 illustrates that the logical functions NOT, AND, NAND, XOR, and

FANOUT can be built from single Toffoli gates. The function OR can be built with two

NOT and one NAND gates using the relation a ∨ b =

∧

b. The ﬁgure also shows

the CNOT gate, which can be viewed as a simpliﬁed representation of the XOR gate.

The Toffoli gate, like the Fredkin gate, thus, represents a universal building block in the

construction of reversible-logic circuits.

I shall now provide an example of a complex circuit exclusively constructed from

CNOT and Toffoli gates, which is called the plain adder. A plain adder performs the

addition of two binary numbers A = a

,...,a

and B = b

,...,b

. This function

entails not only the bit-by-bit addition operations (a

⊕ b

with i = 0 ...n) but also the

computation and addition of the carry bit c

i−1

at each stage i. To construct a plain adder,

one, thus, needs two new gate circuits, which we call SUM and CARRY, and which are

illustrated in Fig. 15.11. It is seen from the ﬁgure that SUM is built from a cascade of

two CNOT gates.

The plain-adder circuit performs the double sum x = a ⊕ b (bit-by-bit addition of

order i) and y = x ⊕ c (addition of the result with carry c of order i − 1), with indices

being omitted here for clarity. The circuit CARRY outputs the carry bit c



= (ab) ⊕

c(a ⊕ b), where c is the carry from order i − 1. It is easily checked that c



is the carry of

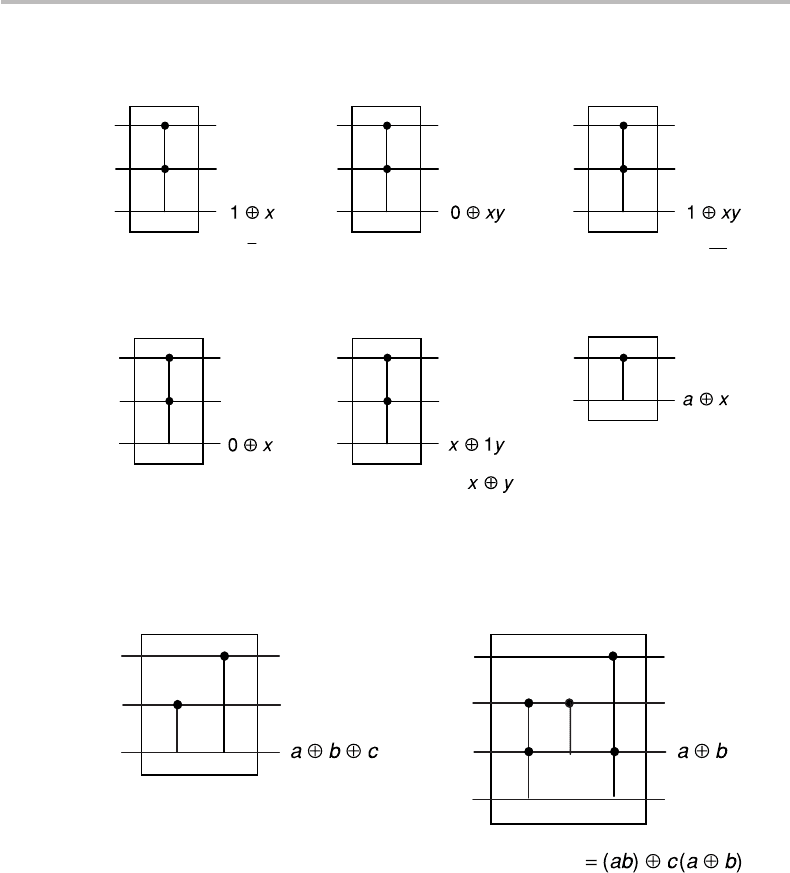
300 Reversible computation

NOT

AND

NAND

XOR

FANOUT

CNOT

Figure 15.10 Logic gates NOT, AND, NAND, FANOUT, and XOR, as built from single Toffoli

gates. The gate CNOT is also shown.

SUM

CARRY

Figure 15.11 Gate circuits SUM and CARRY, built from CNOT and Toffoli gates.

order i of the sum a ⊕ b ⊕ c.

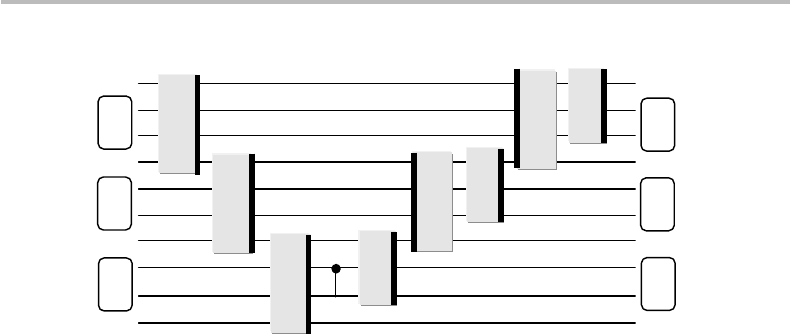
The plain-adder circuit, which performs the computation

D = A + B of two binary numbers A = a

,...,a

and B = b

,...,b

, chosen

here with n = 2 for simplicity,

is shown in Fig. 15.12.

The interpretation of the V-shaped circuit shown in the ﬁgure goes as follows. Consider

ﬁrst the CARRY gates. In the left part of the circuit (the descending branch of the V),

we observe that the carry is computed through a cascade of three CARRY gates, up

Indeed, (a) if a = b = 0thenc



= 0 ⊕ 0c = 0; (b) if a = b = 1thenc



= 1 ⊕ 0c = 1; (c) if a = b then



= 0 ⊕ 1c = c.

As adapted from V. Vedral and M. B. Plenio, Basics of quantum computation. Prog. Quant. Electron., 22

(1998), 1–39.

15.3 Reversible logic gates and computation 301

Figure 15.12 Plain-adder gate circuit, performing the addition of two binary numbers

A = a

and B = b

, with output A = a

and D = A + B = d

. The gates

C and S with a thick bar to the right correspond to the CARRY and SUM gates shown in

Fig. 15.11.ThegateC with a thick bar to the left effects the reverse operation of CARRY.

to the highest order (i = 3), which yields c

= d

(highest-weight bit of D = A + B).

In the right part of the circuit (ascending branch of the V), the reverse operation is

effected,

which resets the bit values initially input to the previous CARRY gate in

the sequence. Second, consider the three SUM gates in the right part of the circuit.

These gates are seen to compute d

= a

⊕ b

⊕ c

i−1

in descending order (from i = 2to

i = 0), with c

= 0. At the bottom of the V, one observes that the reverse CARRY gate

is substituted with a CNOT gate. An easy veriﬁcation shows that such an arrangement

makes it possible to initiate the descending summation d

= a

⊕ b

⊕ c

i−1

from the last

CARRY gate outputs.

As expected from the property of its universal, reversible-logic gate components, the

above plain-adder circuit is fully reversible, meaning that no information is lost (the

simultaneous knowledge of A and D = A + B giving knowledge of B). The function of

the circuit (also referred to as a “quantum network” in QIT jargon), can by symbolized

by the notation

(A, B) → (A, A + B). (15.6)

In the same jargon, the operands A, B are also called registers, by analogy with the

classical or von Neumann (VN) computer, which was described in the previous section.

A remarkable feature of the (A, B) → ( A, A + B) network is that the many “garbage

bits,” which are generated by the intermediate computation steps, are eventually disposed

of. Furthermore, the ancilla bits 0 used at the input (see Fig. 15.12) are all reset to their

initial values, which makes them available for any future use in a larger quantum network.

The reverse operation of CARRY is effected by the same gate as shown in Fig. 15.12, but with the operations

performed in the reverse order, as in a mirror version of the circuitry, or reading the diagram from right to

left.

302 Reversible computation

But we aren’t ﬁnished yet with the plain-adder network: it also reserves some interesting

surprises!

First, the plain-adder network can be used in the reverse order, i.e., feeding input-

(A, B) → (A, A − B)forA ≥ B (15.7)

and

(A, B) → [A, 2

n+1

− (B − A)] for A < B (15.8)

where n + 1 is the size of the second output register. In both cases (A ≥ B or A < B),

the network performs the subtraction function. In the second case it can be shown that

the bit of highest weight is always 1, which represents a “negative-sign bit” for the result

of the difference A − B.

Second, the plain-adder network also makes it possible to perform modular algebra

with the functions of multiplication, and exponentiation. Indeed, modular multiplication

and exponentiation, i.e., (A, B) → (A, A × B) and (A, B) → (A, A

), respectively,

can be performed using the properties

A × B mod m = (A + A +···+A)

B times

mod m, (15.9)

mod m = (A × A ×···×A)

B times

mod m, (15.10)

which apply given any modulus m. Modular algebra is the key to solving quantum-

computation problems, such as the factorization of integers into primes (see

Chapter 20).

In the forthcoming chapters, reversible-logic gates and their networks will not be

used with “classical bits,” but rather with “quantum bits,” or qubits, which hold more

interesting properties and surprises.

15.4 Exercises

15.1 (B): Prove the following alternative deﬁnitions for XOR gates:

a ⊕ b = (a ∨ b) ∧ (

a ∨

= (a ∧

b) ∨(

a ∧ b)

= (a

∧

∧ (

∧ b).

15.2 (B): Prove De Morgan’s law:

(

a ∧ b

)

a ∨

(

a ∨ b

)

a ∧

M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge: Cambridge

University Press, 2000); V. Vedral and M. B. Plenio, Basics of quantum computation. Prog. Quant. Electron.,

22 (1998), 1–39.

15.4 Exercises 303

15.3 (T): Prove by Boolean algebra that the deﬁnition of XOR

a ⊕ b = (a

∧b) ∧(a ∨ b)

is formally equivalent to any of the following three deﬁnitions:

a ⊕ b = (a ∨ b) ∧ (

a ∨

= (a ∧

b) ∨(

a ∧ b)

= (a

∧

∧ (

∧ b).

(Clue: use the distributive property according to which a ∧

(

b ∨c

)

(

a ∧ b

)

∨

(

a ∧ c

)

15.4 (B): What is the Boolean function of the gate circuit?

15.5 (B): Through Boolean logic, show that the circuit arrangement of three successive

CNOT gates, A

CNOT

, B

CNOT

, A

CNOT

CNOT CNOT CNOT

is equivalent to a SWAP gate.

16 Quantum bits and quantum gates

This chapter represents our ﬁrst step into quantum information theory (QIT). The key

to operating such a transition is to become familiar with the concept of the quantum

bit, or qubit, which is a probabilistic superposition of the classical 0 and 1 bits. In the

quantum world, the classical 0 and 1 bits become the pure states |0 and |1, respec-

tively. It is as if a coin can be classically in either heads or tails states, but is now

allowed to exist in a superposition of both! Then I show that qubits can be physi-

cally transformed by the action of unitary matrices, which are also called operators.

I show that such qubit transformations, resulting from any qubit manipulation, can be

described by rotations on a 2D surface, which is referred to as the Bloch sphere.The

Pauli matrices are shown to generate all such unitary transformations. These trans-

formations are reversible, because they are characterized by unitary matrices;this

property always makes it possible to trace the input information carried by qubits.

I will then describe different types of elementary quantum computations performed

by elementary quantum gates, forming a veritable “zoo” of unitary operators, called

I, X, Y, Z , H, CNOT, CCNOT, CROSSOVER or SWAP, controlled-U, and controlled-

controlled-U. These gates can be used to form quantum circuits, involving any number

of qubits, and of which several examples and tools for analysis are provided. Finally, the

concept of tensor product, as progressively introduced through the above description, is

eventually formalized. The chapter concludes with the intriguing noncloning theorem,

according to which it is not possible to duplicate or “clone” a quantum state.

16.1 Quantum bits

In computer science, the binary digit, or bit, represents the elementary unit of infor-

mation. It is a scalar with two possible values, 0 and 1. The bit can also be viewed as

a two-state variable, which can be in either the state 0 or the state 1, with no possible

other or intermediate states. In Shannon’s theory, the bit is also the unit of information,

but is a real number satisfying 0 ≤ x ≤ 1, which expresses the average information

available from a random binary source, which is called entropy. The results of Shan-

non’s information theory, in fact, concern any information sources, including multi-level

or multisymbolic ones, up to any integer number M. In these cases, the bit informa-

tion available from the source is bounded according to 0 ≤ x ≤ log

M. When M is

a power of two (M = 2

), it is possible to encode the different symbols into as many

16.1 Quantum bits 305

binary codewords, and the corresponding sources can be conceived as an extension of

a binary source. Thus, each bit in a given codeword is allowed one out of two pos-

sible states, and this corresponds to the most fundamental representation of classical

information.

In quantum information theory (QIT), and its derivative, quantum computation (QC),

the elementary unit of information is the quantum bit or qubit. As we shall see, the

striking property of the qubit is to escape any deﬁnition of being 0 or 1. It is correct,

however, to say that it can be either 0 or 1. To clarify, somewhat, such a mystery, consider

a closed box with a coin inside. We shake the box. The coin must then be resting in

the heads or tails position (excluding here any other possibility, for simplicity). The

question is, “What is the coin’s position?” The intuitive and classical answer is, “It must

be either heads or tails.” According to the quantum deﬁnition, the coin is described by

a qubit. The answer is that the coin position, or state, is “neither heads nor tails, but a

superposition of both.” As long as we do not open the box, we cannot know in which

state the coin actually exists. By opening the box, we make a measurement of the coin

state, and the outcome is a classical bit of information, namely heads or tails. This basic

example provides an intuitive notion of the nature of the qubit, which I shall formalize

through this chapter.

In the above, we have used different new terms, such as state, superposition of states,

and measurement, which (to some readers) represents as many hints of the domain

of quantum mechanics. In this introductory chapter, we shall approach the notion of

qubit without approaching quantum mechanics any closer. Indeed, there is no need to

present a more complicated picture if we can introduce the qubit and its properties and

formalism by simpler means. We have realized from the preceding explanation that the

qubit is a piece of information that combines in some ways the information of both 0

and 1. Therefore, we may simply view the qubit as a two-dimensional (2D) vector, with

one dimension deﬁning the 0 information component, and the other dimension the 1

information component.

We shall now formalize the 2D vector representation of the qubit. Given a 2D vector

space with basis u, v, one can then deﬁne the qubit state, q, under the linear combination

q = α u + β v, (16.1)

where α, β are complex numbers,

which represent the vector’s coordinates in the

2D space. Assuming that ( u, v) is an orthonormal basis,

and using the column

To recall essential basics, complex numbers z are deﬁned as z = a + ib,where(a, b) are real numbers

and i the “pure imaginary” basis having the property i

=−1. The real numbers a and b are called the

real and the imaginary parts of z, respectively. The length or modulus of z is deﬁned as |z|=

√

+ b

Complex numbers can be equivalently written as z =|z|e

iθ

where θ = tan

−1

(b/a)istheargument of

z,andwheree

iθ

≡ cos θ + isinθ is the imaginary-exponential function. The complex-conjugate of z,

indifferently called z

∗

z,isdeﬁnedasz

∗

z = a − ib =|z|e

−iθ

. A key property is z

∗

z = z

z =|z|

+ b

To recall from vector-space algebra, an orthonormal basis is any set of n vectors u

, u

,..., u

, which

satisfy for all i, j = 1,...,n the scalar-product condition u

· u

= δ

,whereδ

is the Kronecker symbol

(δ

= 1fori = j and δ

= 0fori = j). For i = j, the condition gives u

=| u

= 1, or | u

|=1.

306 Quantum bits and quantum gates

representation for vectors, we have

q = α u + β v = α





+ β





. (16.2)

As detailed further on in this chapter, in QIT a vector or qubit state q is noted instead

as |q, where the arrow |is called a ket (as in the second half of the word bracket).

Consistently, and by analogy with classical bits, the two elementary states u and v

are noted |0 and |1, respectively. The qubit can, thus, be deﬁned as the vector linear

combination:

|q=α|0+β|1. (16.3)

This shows that a qubit can be conceived as a superposition of the two elementary

orthogonal states |0 and |1. In QIT jargon, the complete set of states |0, |1is referred

to as the computational basis. The two complex coordinates α, β, are also called the

qubit amplitudes.

It is seen from the above that, contrary to the classical information bits,thequbit can

be both 0 and 1, or, more accurately, a linear superposition of states 0 and 1. Unlike

classical bits, which correspond to only two possible points on a line (x = 0orx = 1),

qubits can correspond to an inﬁnity of points in a 2D space. We shall see later how such

points can be represented visually.

As we have seen from Chapter 15, the classical or von Neumann computer retrieves

information by reading the bit contents in its inner memory. Any such reading operation

is, thus, analogous to a physical measurement of the memory contents. Likewise, the

information carried by qubits can be measured. The key difference between the classical

bit and the qubit is that, as we have seen, the latter is a superposition of the states |0and

|1 in a 2D space. It is not possible to physically measure the two complex amplitudes

α, β, which deﬁne the qubit state. This amounts to saying that it is not possible to

“measure” a qubit state. Rather, any physical measurement of a qubit yields a classical

bit, which must be either 0 or 1. Such a measurement is not deterministic, but associated

with certain probabilities. The probability that the qubit measure yields the bit 0 is

proportional to |α|

, and that of yielding the bit 1 is proportional to |β|

. Since there

exist only two measurement possibilities, we must have

|α|

+|β|

= 1. (16.4)

Since |α|

+|β|

is the length or magnitude of the qubit vector, this result expresses

the property that the qubit is a unitary vector. Thus a qubit with α = 0orβ = 0exists

in the pure state |0 or |1. The corresponding measurements yield the exact result 0

with probability |α

|=1, or 1, with probability |β

|=1, respectively. Another case

of interest is |α|

=|β|

= 1/2, where the measurement outcome has equal chances of

being 0 or 1. In general, there is no way to tell the measurement outcome, even if the

qubit state is known, because the measurement is probabilistic. Given the property in

Eq. (16.4) concerning the qubit amplitudes, the most general deﬁnition of the qubit is,