Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

14.2 Nonlinear channel 277

the SHT boundary, the more sensitive the system SER is to SNR and signal power.

Also, the more complex the error-correction codes to bring the BER to low values.

Given constraints in power and noise, in BER requirement after code correction, in

code-correction complexity, and, ﬁnally, in modulation-format technologies, the difﬁcult

task for communications engineers is to ﬁnd the right tradeoffs between academic and

practical engineering solutions.

14.2 Nonlinear channel

Shannon’s information theory and all its subsequent developments have always been

based on the assumption of channel linearity. The principle of channel linearity can be

summarized by two basic conditions:

(a) Assuming signal input to the channel with power P, the signal output power is of

the form P



= λP, where λ is a real constant that is power independent (λ<1for

lossy channels, λ = 1 for transparent or lossless channels, and λ>1 for channels

with internal ampliﬁcation or gain);

(b) The channel noise N is added linearly to the signal power (additive noise), namely

the total output power is of the form P



= κ P + µN, where µ is a real constant

that is power independent.

Condition (a) implies that the signal can be increased to an arbitrarily high power level,

without any changes in the channel’s properties, as provided by information theory.

Condition (b) implies that the transmission pipe in the channel is free from any power-

dependent signal degradation effects. In the physical world, such effects are referred to

as nonlinearities. Such nonlinearities are usually not observed in vacuum or atmospheric

space.

However, they are observed in transmission media such as optical ﬁbers, for

instance. The advent of high-speed optical telecommunications in the last 20 years has

come with the discovery of various types of nonlinearity, namely, Raman and Brillouin

scattering, self- and cross-phase modulation, and four-wave mixing. Such nonlinearities

cause power limitations (hence SNR and BER limitations) in ﬁber-optic systems. In

the following, I shall focus on ﬁber-optic systems as an illustration of the nonlinear

communications channel.

An optical ﬁber is a highly transparent transmission medium. However, optical signals

are attenuated on propagation therein, according to an exponential law P



= λP =

P exp(−αL), where L is the ﬁber length and α the attenuation coefﬁcient. For lengths

of 50 km and 100 km, the relative signal attenuation or power loss is typically 90%

(λ = 0.1) or 99% (λ = 0.01) respectively. To compensate for ﬁber loss, ﬁber-optic

systems use in-line optical ampliﬁers. Such ampliﬁers are periodically placed every

50–100 km (depending on applications) to produce a signal gain g = 1/λ, such that the

At least with the power levels used in telecommunications. The atmosphere is made of atomic and molecular

matter, which may exhibit nonlinear absorption or scattering at certain frequencies and powers, and a vacuum

is nonlinear from the high-energy physics or quantum-electrodynamics viewpoint.

278 Gaussian channel and Shannon–Hartley theorem

signal power at the ampliﬁer output is P



= gλP ≡ P. The ampliﬁed ﬁber-optic link is

said, therefore, to be transparent. However, the ampliﬁcation process produces additive

noise, which accumulates linearly along the transparent link, each ampliﬁcation stage

contributing to a noise increment.

Overlooking any effect contributed by the optical ﬁber, an ampliﬁed ﬁber-optic link

is intrinsically linear.

A simple justiﬁcation comes as follows. At the end of the

link, the optical signal is converted by the receiver into a photocurrent. It can be

shown that the dominant noise component in the receiver photocurrent output is of the

form:

= 2PN, (14.27)

where P is the optical power input to the (transparent) link and, hence, to the end

receiver, and N is the optical ampliﬁer noise accumulated along the link, which is

power-independent.

The electrical signal power is of the form

= P

. (14.28)

The electrical signal-to-noise ratio (SNR) is, thus,

SNR =

2PN

≡

, (14.29)

whose noise denominator is now seen to be independent of the signal power. Thus, the

SNR scales linearly with the input (optical) power, which is the linearity condition for the

communication channel. But the transmission medium, the optical ﬁber, is intrinsically

nonlinear. It is beyond the scope of this book to detail the different types and causes of

ﬁber nonlinearities.

The introduction of channel nonlinearity in the ﬁeld of information theory is relatively

recent (2001).

As we shall see, this new hypothesis is rich in implications in the analysis

of channel capacity, in particular for optical transmission systems. We shall, thus, assume

that the nonlinear channel noise, N

∗

, has the power-dependent form

∗

(P) = N + sP, (14.30)

where N is the linear channel noise (P = 0) and sP is the power-dependent contribution

to the channel noise, which is attributed to optical ﬁber nonlinearities. The nonlinearity

parameter s can be written as

s = 1 −exp

−





, (14.31)

As in any ampliﬁers, the ampliﬁcation factor (gain) of optical ampliﬁers saturates with increasing signal

power. However, optical ampliﬁers deployed in transmission systems are designed to yield constant gain

regardless of signal power changes.

See, for instance: E. Desurvire, Erbium-Doped Fiber Ampliﬁers, Devices and System Developments (New

York: J. Wiley & Sons, 2002), Ch. 3.

P. P. Mitra and J. B. Stark, Nonlinear limits to the information capacity of optical ﬁber communications.

Nature, 411 (2001), 1027; for a tutorial introduction, see also E. Desurvire, Erbium-Doped Fiber Ampliﬁers,

Devices and System Developments (New York: J. Wiley & Sons, 2002), Ch. 3.

14.2 Nonlinear channel 279

where P

is the power threshold at which nonlinearity comes into effect. The exact

deﬁnition of P

in relation to the various ﬁber-optics link parameters can be found in the

aforementioned references. The above deﬁnition of the nonlinearity parameter s shows

that nonlinearity is negligible, or the optical channel is linear, for P  P

or s → 0

(or sP  N ), which, according to Eq. (14.30) gives the power-independent, additive

channel noise N

∗

(P) ≈ N . In the general case, we see from the relation N

∗

(P) =

N + sP that a fraction sP of signal power is effectively converted into nonlinear noise.

Because of energy conservation, the received signal power at the end of the link is not P,

but rather P

∗

= P(1 −s). The actual SNR is now SNR

∗

= P

∗

, which reduces to

SNR

∗

= P/N in the linear limit P  P

(s → 0). We can now evaluate the nonlinear

channel capacity. According to the Shannon–Hartley theorem (SHT), Eq. (14.18), the

channel capacity ((bit/s)/Hz) is given by:

C = log



1 +

∗



= log



1 +

P(1 −s)

N + sP



(14.32)

= log







1 +

1 − s

1 + s







Replacing the deﬁnition of the nonlinearity parameter s in the above yields:

C = log











1 +

exp

−





1 +

1 − exp

−















= log











1 +

exp





exp





− 1











(14.33)

The result in Eq. (14.33) shows that in the high-power limit P/P

→∞, the channel

capacity reduces to C = log(1 + ε) with ε → 0, or C → 0. Nonlinearity, thus, asymptot-

ically obliterates channel capacity. Since in the linear regime channel, capacity increases

with signal power, we then expect that a maximum can be reached at some power value.

It can be shown that such a maximum capacity is reached for the optimal signal power

opt

as analytically deﬁned:

opt





. (14.34)

280 Gaussian channel and Shannon–Hartley theorem

Replacing this deﬁnition of P

opt

into Eq. (14.33) yields the maximum achievable channel

capacity C

max

log



√



. (14.35)

A different model that I developed,

which takes into account the quantum nature of

ampliﬁer noise leads to an alternative deﬁnition C



of the channel capacity:



= log







1 +

P(1 −s)

1 + 2N + s



1 +

1 − s









= log







1 +

1 − s

2 +

+ s



1 +

1 − s









(14.36)

The new deﬁnition of capacity in Eq. (14.36) yields different expressions for the optimal

power and maximum capacity, namely P



opt

and C



max

, as deﬁned by:



opt



(1/2 + N )P



, (14.37)



max

log

√

3(1 + 2N )

. (14.38)

We note from Eqs. (14.34)–(14.35) and Eqs. (14.37)–(14.38) that the optimal powers

opt

, P



opt

and maximal capacities C

max

, C



max

actually have very similar values. With

respect to the classical model, the quantum model of the nonlinear channel provides a

small correction to the maximum SNR of the order of 2

−1/3

≈ 0.8, which, in base-2

logarithms, represents about 30%.

Figure 14.6 shows plots of thee nonlinear-channel capacities C, C



(according to the

two above models), as plotted vs. the linear SNR, i.e., SNR = P/N , as expressed in

decibels,

with different parameter choices for N and P

. The SHT capacity corre-

sponding to the linear-channel case is also shown. Figure 14.6(a) corresponds to the

worst case of a channel with a nonlinear threshold relatively close to the linear noise

(N = 5 and P

= 15). In contrast, Figure 14.6(b) corresponds to the case of a compara-

tively low linear-noise channel having a relatively high nonlinear threshold (N = 1 and

= 100). It is seen from the ﬁgure that in both cases, and regardless of the nonlinear

model (classical or quantum), the channel capacity is bounded to a power-dependent

maximum, unlike in the linear information theory where from SHT the capacity increases

as log(SNR).

E. Desurvire, Erbium-Doped Fiber Ampliﬁers, Devices and System Developments (New York: J. Wiley &

Sons, 2002), Ch. 3.

With SNR(dB) = 10 log

(SNR).

14.2 Nonlinear channel 281

−10 −5

0510

SNR (dB)

Channel capacity C,C´ ((bit/s)/Hz)

Linear channel (SHT)

(a)

−

50 5 201510

SNR (dB)

Channel capacity C,C´ ((bit/s)/Hz)

Linear channel (SHT)

(b)

Figure 14.6 Nonlinear channel capacities C, C



, as functions of linear signal-to-linear-noise ratio

P/N according to classical and quantum models with SHT linear-channel capacity shown for

reference (thick line), with dimensionless parameters (a) N = 5andP

= 15, and (b) N = 1

and P

= 100.

The consequences of these developments concerning nonlinear channels remain to

be fully explored. It is important to note that the assumption of channel nonlinearity

does not affect the key conclusions of Shannon’s (linear) information theory, namely the

channel coding theorem and the SHT. Indeed, error-correction codes are used in realistic

(nonlinear) optical communication systems to enhance SNR and BER performance. The

fact that in these nonlinear optical channels the noise is power-dependent does not affect

the effectiveness of such codes. The key conclusion is that the capacity limits imposed

by Shannon’s information theory still apply, despite the new complexities introduced

by channel nonlinearity, which introduces yet another upper bound. It should not be

interpreted, however, that nonlinearity deﬁnes an “ultimate capacity limit” for optical

communication channels, present or future. Indeed, optical ﬁber design makes it possible

effectively to reduce ﬁber nonlinearity by increasing the ﬁber core size (referred to as the

“effective area”), so as to decrease the nonlinearity threshold, P

, and, hence, effectively

achieve the operating conditions P  P

(s → 0). Furthermore, there exist several

types of “countermeasures” and power–SNR tradeoffs to alleviate optical nonlineari-

ties, which it is beyond the purpose of this chapter to describe. Overall, the key conclusion

282 Gaussian channel and Shannon–Hartley theorem

is that the optical communication channel, albeit nonlinear, can be made to operate as a

linear channel, which is, therefore, essentially compliant to the capacity limits set up by

Shannon’s coding theorem.

14.3 Exercises

14.1 (M): The signal-to-noise ratio in a continuous channel is SNR =+12.5 dB. What

is the channel capacity? Suggest a Reed–Solomon block code for which the

capacity could be approached within approximately one bit.

14.2 (T): Show that the differential conditional entropy

H(Y |X ) =−



p(y|x) p(x)logp(y|x)dxdy

reduces after analytical computation to

H(Y |X ) = log

(

2πeσ

14.3 (T): Show that the capacity of a Gaussian channel with NRZ/OOK modulation

rapidly converges with increasing signal power to the upper limit:

C = 1 (bit/s)Hz.

Clues:

(a) Assume a binary input signal x

∈ X ={x

, x

}taking the values x

= a and

=−a, and a continuous output y ∈ Y ,

(b) Deﬁne the mutual information as

H(X ; Y ) =





dyp(x

, y,)log



p(x

, y)

p(x

)p(y)



)as:

p(y|x

) =

√

2π

exp



−

(y − x

)

2σ



where σ

is the channel noise variance.

(d) Show that the channel capacity is a function of the “bit SNR” parameter

≡ a

/(2σ

) and numerically determine the limit for increasing S

15 Reversible computation

This chapter makes us walk a few preliminary, but decisive, steps towards quantum

information theory (QIT), which will be the focus of the rest of this book. Here, we shall

remain in the classical world, yet getting a hint that it is possible to think of a different

world where computations may be reversible, namely, without any loss of information.

One key realization through this paradigm shift is that “information is physical.” As we

shall see, such a nonintuitive and striking conclusion actually results from the age-long

paradox of Maxwell’s demon in thermodynamics, which eventually found an elegant

conclusion in Landauer’s principle. This principle states that the erasure of a single bit

of information requires one to provide an energy that is proportional to log 2, which,

as we know from Shannon’s theory, is the measure of information and also the entropy

of a two-level system with a uniformly distributed source. This consideration brings

up the issue of irreversible computation. Logic gates, used at the heart of the CPU in

modern computers, are based on such computation irreversibility. I shall then describe the

computers’ von Newman’s architecture, the intimate workings of the ALU processing

network, and the elementary logic gates on which the ALU is based. This will also

provide some basics of Boolean logic, expanding on Chapter 1, which is the key to the

following logic-gate concepts. As I shall describe, a novel concept for logic gates (and,

hence, their associated circuits or networks), can be designed to provide truly reversible

computation.

15.1 Maxwell’s demon and Landauer’s principle

The QIT story begins with a strange machine devised in 1871 for a thought experiment

by the physicist J. C. Maxwell. Such a machine – if one were ever able to construct it –

would violate the second principle of thermodynamics! As Maxwell describes in his

theory of heat:

One of the best established facts in thermodynamics is that it is impossible in a system enclosed

in an envelope which permits neither change of volume nor passage of heat and in which both the

temperature and the pressure are everywhere the same, to produce any inequality of temperature

or of pressure without the expenditure of work. This is the second law of thermodynamics, and

See http://en.wikipedia.org/wiki/Maxwell%27s_demon; http://users.ntsource.com/∼neilsen/papers/demon/

node3.html.

284 Reversible computation

(a)

(b)

´<

´´>

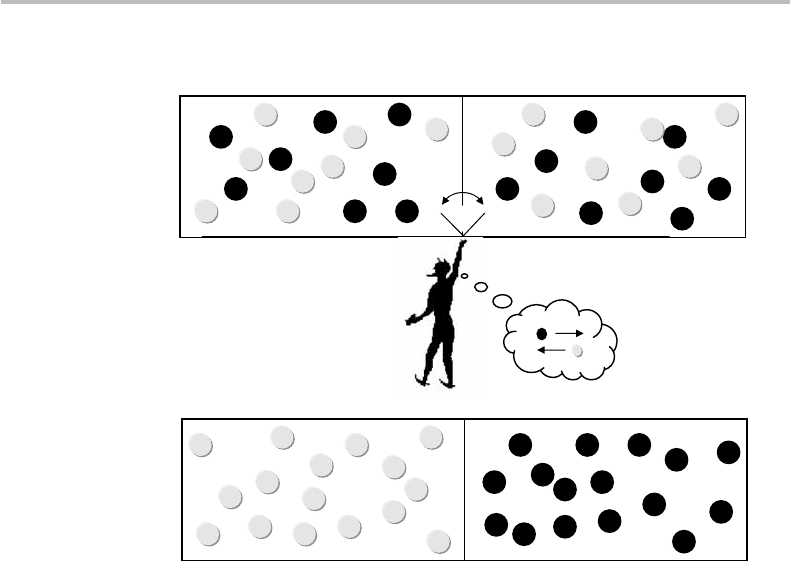
Figure 15.1 Maxwell’s demon thought experiment: (a) initially, the gas molecules are evenly

spread between two parts A and B (dark = fast, clear = slow), with homogeneous temperature

T , and (b) after the demon sorted molecules according to speed, showing lower temperature T



part A and higher temperature T



in part B.

it is undoubtedly true as long as we can deal with bodies only in mass, and have no power of

perceiving or handling the separate molecules of which they are made up. But if we conceive

a being, whose faculties are so sharpened that he can follow every molecule in its course, such

a being, whose attributes are still as essentially ﬁnite as our own, would be able to do what is

at present impossible to us. For we have seen that molecules in a vessel full of air at uniform

temperature are moving with velocities by no means uniform, though the mean velocity of any

great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that

such a vessel is divided into two portions, A and B, by a division in which there is a small hole,

and that a being, who can see the individual molecules, opens and closes this hole, so as to allow

only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to

A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in

contradiction to the second law of thermodynamics.

A basic illustration of Maxwell’s machine is provided in Fig. 15.1. As Maxwell

describes it, the machine consists of a gas container or “vessel,” which is separated

by a wall into two chambers, A and B. The gas absolute temperature T is uniform,

To recall, the absolute temperature is expressed in units of kelvin (K). It has a one-to-one correspondence

with the Celsius (C) temperature scale, with absolute zero being 0 K =−273

◦

C and the melting-ice

temperature being 0

◦

C =+273 K.

15.1 Maxwell’s demon and Landauer’s principle 285

and is given by the formula E = (3/2)k

T , where E is the average kinetic energy of

the gas molecules (k

= Boltzmann’s constant). Both temperature and energy represent

macroscopic measures, as individual molecules don’t have a “temperature” and have

different velocities of their own, some moving slower and some moving faster. As the

ﬁgure shows, an imaginary, witty but not malicious creature (later dubbed “Maxwell’s

demon”) guards a trapdoor, which allows individual molecules to pass from A to B or

the reverse, without friction or inertia. The demon checks out the molecules’ velocities

and allows only the faster ones (E



> E) to pass from A to B, and only the slower ones



< E) to pass from B to A. After a while, most of the fast molecules are found in B,

while most of the slow ones are in A. As a result, the gas temperature in A (T



)islower

than that in B (T



), with T



< T < T



The simultaneous heating of part B and cooling of part A, which is accomplished by

the demon without deploying energy or work, is in contradiction to the second law of

thermodynamic. This second law stipulates, in its simplest formulation, that: “Heat does

not ﬂow spontaneously from a cold to a hot body of matter.” Since heat is a measure

of the average kinetic energy of the gas, it has a natural tendency to diffuse from hot to

cold bodies, and not the reverse. Another formulation of the second law is that: “In an

isolated system, entropy as a measure of disorder or randomness can only increase.” Let

us have a closer look at this entropy notion. In Appendix A, we have seen that a system

of particles that can be randomly distributed in W arrangement possibilities into a set

of distinct boxes, called “microstates,” is characterized by an entropy H. This entropy

represents the inﬁnite limit, normalized to the number of particles, of the quantity log W .

Hence, the greater W or H , the more randomly distributed the system, which justiﬁes

the notion of entropy as a physical measure of disorder. By separating and ordering the

gas molecules into two distinct families (slow and fast), the demon decreases the global

randomness of the system, since there is a smaller number of microstate arrangements W

for each of the initial molecules, the system’s entropy log W is, thus, decreased, which is

indeed in contradiction to the second law because the demon apparently did not perform

any work.

At the time, the conclusion reached by Maxwell to solve this paradox was that the

second principle only applies to large numbers of particles as a statistical law, i.e., to

be used with certain conﬁdence at a macroscopic, rather than at a microscopic level.

In the ﬁrst place, Maxwell’s paradox was never intended to challenge the second law.

Yet, it kept puzzling scientists for generations with many unsolved issues. In 1929, for

instance, L. Szil

ard observed that in order to measure molecular velocities, the demon

should spend some kind of energy, such as that of photons from a ﬂashlight, to spot the

slow or fast molecules, and then decide from the observation whether or not to open the

trapdoor. Each of such measurements and the generation of photons would then increase

the system’s entropy, which should balance out the other effect of entropy decrease.

In 1951, L. Brillouin observed that in order to distinguish molecules by use of light

photons, the photon energy would have to supersede that of the ambient electromagnetic

radiation, thus bringing a quantum of heat k

T into the system. To move the trapdoor,

the “demon” must also be material. Thus, some form of heat transfer should occur during

the process, resulting in the heating of both the demon and the gas, canceling the cooling

286 Reversible computation

effect of molecule separation. In 1963, R. Feynmann observed that the demon would

not be able to get rid of the heat gained in his molecule measurements, ending up in

“shaking into Brownian motion” with the inability to perform the task!

Most of the above conjectures, along with the multiplication of improved “demon

engines,” contributed to turn Maxwell’s initial paradox into an ever-deepening enigma.

This is how the concept of information entropy came into the picture. Szil

ard considered

a demon engine processing just a single gas molecule. If the demon knew where the

molecule was located, then he could move a frictionless piston to conﬁne it where

it belonged, without any work expenditure! Then the pressure effect of the molecule

on the piston could be used to generate work, such as lifting a weight. The intuitive,

yet not consolidated idea, was that the entropy bookkeeping could be balanced should

some positive entropy be associated with the information concerning molecules or the

demon’s memory itself. Either the demon keeps track of any of its binary decisions

(open trapdoor to molecule coming from A or B) or it erases them. In the ﬁrst case,

the demon’s memory space expands, which goes together with an entropy increase

(number of accessible memory states in the demon’s mind). At some point, however,

the memory space is exhausted, and information must be erased. In the second case,

the memory is cleared one bit at a time prior to the next binary decision. Whether the

memory is cleared at once or bit after bit after each demon operation, the action of

erasure is irreversible.

According to thermodynamics, irreversible processes generate

positive entropy. Therefore, the erasure of information must increase the entropy of

the surrounding environment. Such a revolutionary concept was initially suggested by

J. von Neumann

and then formalized in 1961 by R. Landauer. The key conclusion

takes the form of Landauer’s principle (or the Landauer bound or limit,orthevon

Neumann–Landauer bound):

The energy dissipated into the environment by the erasure of a single bit of information is at least

equal to k

T log 2. The environment entropy increases by at least k

log 2.

Landauer’s principle, thus, provides a lower bound on the energy dissipation and

entropy increase associated with information erasure. It is not coincidental that this

minimum is proportional to log 2 (natural logarithm). Without pretending to provide a

formal demonstration of this result, consider the following. The memory to be erased

can be viewed as a binary source X =

{

1, 0

}

having a uniform distribution, i.e., p(1) =

p(0) = 1/2 (the probability that the memory bit is either 1 or 0). As we have seen in

Chapter 3,theself-information associated with any of the two events x ∈ X is I (x) =

−log

[p(x)] ≡−log

(1/2) = log

2, as expressed in nats. The source’s entropy H (X)

corresponds to the average information

I (x)=−p(1) log

[p(1)] − p(0) log

p[(0)]

= 0.5log

2 + 0.5log

2 = log

For a given memory address, the initial state is the bit value 0 or 1. Once cleared, the bit value is reset to 0

(for instance). From this ﬁnal state, it is not possible to decide whether the initial state was the bit value 0

or 1, and so on for all previously recorded states, which illustrates the irreversibility of the erasure process.

See http://en.wikipedia.org/wiki/Landauer%27s_principle.