Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

13.3 Shannon’s channel coding theorem 257

••••••

•• •

••••••• ••

•••••

Source

)(

XnH

typical

inputs

(

)

typical

outputs

most likely

origins for each

)(

XYnH

(

)

XnH

most likely

outcomes for each

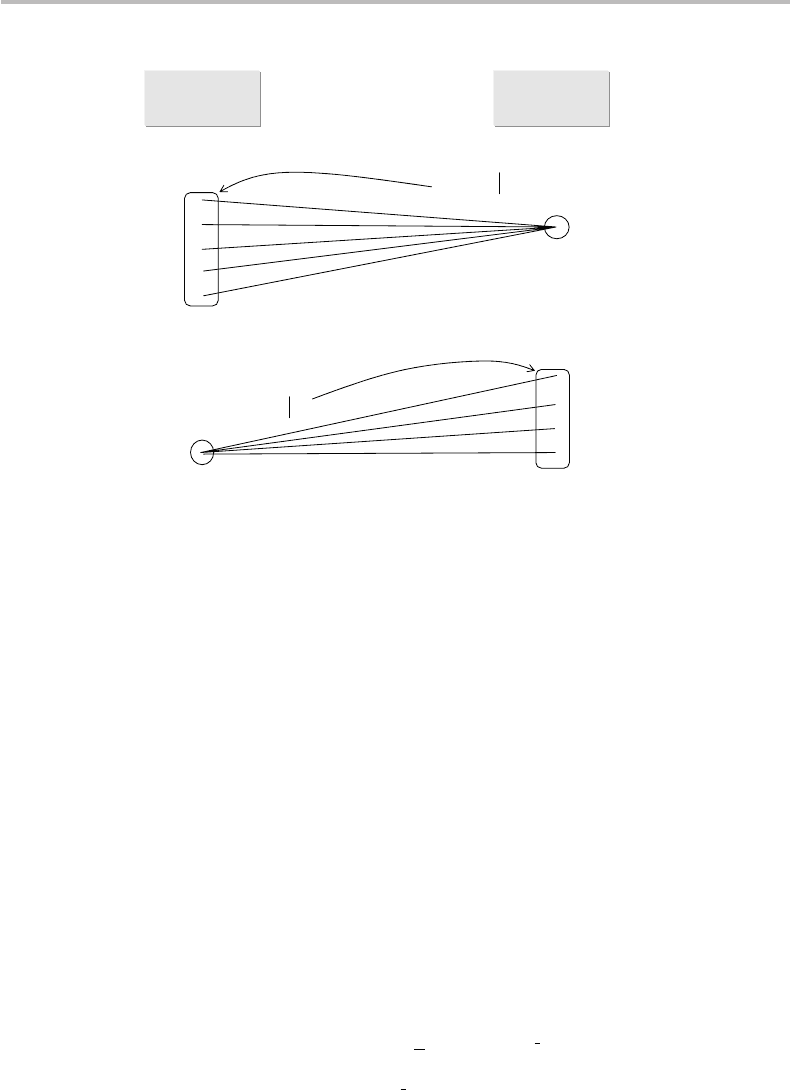
Figure 13.5 Noisy communication channel relating input source X (sequences x) and output

source Y (sequences y), showing the numbers of most likely inputs x (typical set of X), of most

likely outputs y (typical set of Y ), of most likely origins for given output y

, and of most likely

outcomes for given input x

Assume next that a particular output sequence y

is received. What is the no-error

probability,

p, that y

exclusively corresponds to the message x

? As we have seen, for

any given output message y

there exist α = 2

nH(X|Y )

most likely origins x

. On the other

hand, the probability that the originator message is not x

p = 1 − p(x

). Thus, we

obtain from Eq. (13.28) the no-error probability:

p =

[

1 − p(x

)

]

={1 −2

n[R−H (X)]

}

nH(X|Y )

. (13.29)

Since we assumed R < C = H (X ) − H (X |Y ), we have R − H (X) < −H (X|Y )or

R − H (X) =−H (X|Y ) −ε where ε is a positive nonzero number (ε>0). Replacing

this relation into Eq. (13.29) yields

p ={1 − 2

−n[H (X|Y )+ε]

}

nH(X|Y )

. (13.30)

We now take the limit of the probability

p for large sequence lengths n. We substitute

u = 2

nH(Y |X)

and v = 2

−nε

into Eq. (13.30) and take the limit of large n to obtain:

p =

1 −

= e

u log(1−

)

≈ e

u(−

)

= e

−v

≈ 1 −v = 1 −2

−nε

(13.31)

In the limit n →∞, we, thus, have

p → 1, which means that any output message y

corresponds exclusively to an input message x

.Theerror probability, p

= 1 −

258 Channel capacity and coding theorem

becomes identically zero as the sequence length n becomes large, which means that,

under the above prerequisites, any original message can be transmitted through a noisy

channel with asymptotically 100% accuracy or zero error.

Concerning binary channels, the above conclusion can be readily reformulated in

terms of the “block code” concept introduced in Chapter 11, according to the following:

Given a noisy binary communication channel with capacity C, there exists a block code (n, k)

of 2

codewords of length n, and code rate R = k/n ≤ C, for which message codewords can be

transmitted through the channel with an arbitrary small error ε.

The above constitutes the formal demonstration of the CCT, as in accordance with

the original Shannon paper. Having gone through this preliminary, but somewhat math-

ematically abstract, exercise, we can now revisit the CCT through simpler approaches,

which are more immediately intuitive or concrete. The following, which includes three

different approaches is inspired from reference.

Approach 1

Recall the example of the “noisy typewriter” channel described in Chapter 12 and

illustrated in Fig. 12.4. The noisy typewriter is a channel translating single-character

messages from keyboard to paper. But any input character x

(say, J) from the keyboard

results in a printed character y

, which has equal chances of being one of three possible

characters (say, I, J, K). As we have seen earlier (Section 13.1, Example 3), it is possible

to extract a subset of triplets from all the 26 possible output messages. If we add

the space as a 27th character, there exist exactly 27/3 =9 such triplets. Such triplets are

called nonconfusable outputs, because they correspond to a unique input, which we call

distinguishable. The correspondence between this unique input and the unique output

triplet is called a fan. Thus in the most general case, inputs are said to be distinguishable

if their fans are nonconfusable or do not overlap.

We shall now use the concept of distinguishable inputs to revisit the CCT.

Figure 13.5 illustrates the correspondence between the typical set of input sequences

nH(X)

elements) and the typical set of output sequences (2

nH(Y )

elements). It is seen

that a fan of 2

nH(Y |X)

most likely (and equiprobable) output sequences of the typical set

of Y

corresponds to any input sequence x

of the typical set of X

. Deﬁne M as the

number of nonconfusable fans, i.e., the fans that are attached to distinguishable input

sequences. The number of output sequences corresponding to the M distinguishable

inputs is, thus, M2

nH(Y |X)

. In the ideal case, where all inputs are distinguishable (or all

fans are nonconfusable), we have M2

nH(Y |X)

= 2

nH(Y )

. If some of the fans overlap, we

have M2

nH(Y |X)

< 2

nH(Y )

. The most general case, thus, corresponds to the condition

nH(Y |X)

≤ 2

H(Y )

, (13.32)

A. A. Bruen and M. A. Forcinito, Cryptography, Information Theory and Error-Correction (New York:

John Wiley & Sons, 2005), Ch. 12.

13.3 Shannon’s channel coding theorem 259

or, equivalently,

M ≤ 2

nH(Y )−nH(Y|X )

= 2

n[H (Y )−H (Y |X )]

↔

M ≤ 2

nH(X;Y )

≤ 2

(13.33)

where C = max H (X; Y ) is the binary-channel capacity (nC being the capacity of the

binary channel’s nth extension, i.e., using messages of n-bit length). If one only chooses

distinguishable input sequences to transmit messages at the information or code rate

R, one has M = 2

possible messages, which gives R = (log M)/n. Replacing this

deﬁnition into Eq. (13.33) yields the condition for the channel rate:

R ≤ C. (13.34)

The fundamental property expressed in Eq. (13.34)isthatthe channel capacity represents

the maximum rate at which input messages can be made uniquely distinguishable,

corresponding to accurate transmission. We note here that the term “accurate” does

not mean 100% error free. This is because the M2

nH(Y |X)

nonconfusable fans of the

M distinguishable input messages are only most likely. But by suitably increasing the

message sequence length n, one can make such likelihood arbitrarily high, and thus

the probability of error can be made arbitrarily small.

While this approach does not constitute a formal demonstration of the CCT (unlike

the analysis that preceded), it provides a more intuitive and simple description thereof.

Approach 2

This is similar to the ﬁrst approach, but this time we look at the channel from the

output end. The question we ask is: what is the condition for any output sequence to be

distinguishable, i.e., to correspond to a unique (nonconfusable) fan of input sequences?

Let us go through the same reasoning as in the previous approach. Referring again to

Fig. 13.5, it is seen that a fan of 2

nH(X|Y )

most likely (and equiprobable) input sequences

of the typical set of X

corresponds to any output sequence y

of the typical set of Y

Deﬁne M as the number of nonconfusable input fans, i.e., the fans that are attached to

distinguishable output sequences. The number of input sequences corresponding to the

M distinguishable outputs is, thus, M2

nH(X|Y )

. Since there are 2

nH(X)

elements in the

typical set X

,wehaveM2

nH(X|Y )

≤ 2

nH(X)

and, hence,

M ≤ 2

n[H (X)−nH(X |Y )]

= 2

nH(Y ;X)

= 2

nH(X;Y )

≤ 2

(13.35)

where we used the property of mutual information H(Y ; X) = H (X; Y ). The result in

Eq. (13.35) leads to the same condition expressed in Eq. (13.34), i.e., R ≤ C, which

deﬁnes the channel capacity as the maximum rate for accurate transmission.

260 Channel capacity and coding theorem

Approach 3

The question we ask here is: can one construct a code for which the transmission

error can be made arbitrarily small? We show that there is at least one such code.

Assume a source X for which the channel capacity is achieved, i.e., H(X ; Y ) = C, and

a channel rate R ≤ C. We can deﬁne a code with a set of 2

codewords (2

≤ 2

chosen successively at random from the typical set of 2

nH(X)

sequences, with a uniform

probability. Assume that the codeword x

is input to the channel and the output sequence y

is received. There is a possibility of transmission error if at least one other input sequence

k=i

can result in the same output sequence y. The error probability p

≡ p(x = x

)of

the event x = x

occurring satisﬁes:

= p(x

= x

or x

= x

or ...x

= x

)

≤ p(x

= x

) + p(x

= x

) +···p(x

= x

(13.36)

Specifying the right-hand side, we obtain:

≤ (2

− 1)

nH(X|Y )

nH(X)

. (13.37)

This result is justiﬁed as follows: (a) there exist 2

− 1 sequences x

k=i

in the codeword

set that are different from x

, and (b) the fraction of input sequences, which output in y

is 2

nH(X|Y )

nH(X)

. It follows from Eq. (13.37) that

p < 2

nH(X|Y )

nH(X)

= 2

n[H (X|Y )−H (X)]

= 2

−n(C−R)

(13.38)

which shows that since R < C the probability of error can be made arbitrarily small

with code sequences of suitably long lengths n, which is another statement of the

CCT.

The formal demonstration from the original Shannon paper, completed with the three

above approaches, establishes the existence of codes yielding error-free transmission,

with arbitrary accuracy, under the sufﬁcient condition R ≤ C. What about the proof

of the converse? Such a proof would establish that error-free transmission codes make

R ≤ C a necessary condition. The converse proof can be derived in two ways.

The ﬁrst and easier way, which is not complete, consists of assuming an absolute

“zero error” code, and showing that this assumption leads to the necessary condition

R ≤ C. Recall that the originator source has 2

possible message codewords of n-bit

length. With a zero-error code, any output bit y

of a received sequence must correspond

exclusively to an input message codeword bit x

. This means that the knowledge of

is equivalent to that of x

, leading to the conditional probability p(x

) = 1, and

to the conditional channel entropy H (X|Y ) = 0. As we have seen, the entropy of the

n-bit message codeword source, X

,isH (X

) = nH(X). We can also assume that

the message codewords are chosen at random, with a uniform probability distribution

p = 2

−nR

, which leads to H (X

) = nR and, thus, H (X) = R. We now substitute the

13.3 Shannon’s channel coding theorem 261

above results into the deﬁnition of mutual information H (X; Y ) to obtain:

H(X ; Y ) = H (X) − H (Y |X) ↔

H(X ) = H (X; Y ) + H (Y |X) ↔ (13.39)

R = H(X; Y ) + 0 ≤ max H (X; Y ) = C,

which indeed proves the necessary condition R ≤ C. However, this demonstration does

not constitute the actual converse proof of the CCT, since the theorem concerns codes that

are only asymptotically zero-error codes, as the block length n is increased indeﬁnitely.

The second, and formally complete way of demonstrating the converse proof of the

CCT is trickier, as it requires one to establish and use two more properties. The whole

point may sound, therefore, overly academic, and it may be skipped, taking for granted

that the converse proof exists. But the more demanding or curious reader might want

to go the extra mile. To this intent, the demonstration of this converse proof is found in

Appendix L.

We shall next look at the practical interpretation of the CCT in the case of noisy,

symmetric binary channels. The corresponding channel capacity as given by Eq. (13.5),

is C = 1 − f (ε) = 1 +ε log ε + (1 −ε)log(1− ε), where ε is the noise parameter or,

equivalently, the bit error rate (BER). If we discard the cases of the ideal or noiseless

channel (ε = f (ε) = 0) and the useless channel (ε = 0.5, f (ε) = 1), we have 0 <

| f (ε)| < 1 and, hence, the capacity C < 1, or strictly less than one bit per channel

use. According to the CCT, the code rate for error-free transmission must satisfy R <

C, here R < C < 1. Thus block codes (n, n) of any length n,forwhichR = n/n =

1 are not eligible. Block codes (n, k) of any length n,forwhichR = k/n > C are

not eligible either. The eligible block codes must satisfy R = k/n < C. To provide

an example, assume for instance ε = 0.01, corresponding to BER = 1 ×10

−3

.We

obtain C = 0.9985, hence the CCT condition is R = k/n < 0.9985 ... Consider now

the following possibilities:

First, according to Chapter 11, the smallest linear block code, (7, 4), has a length

n = 7, and a rate R = 4/7 = 0.57. We note that although this code is consistent with

the condition R < C, it is a poor choice, since we must use n − k = 3 parity bits

for k = 4 payload bits, which represents a heavy price for a bit-safe communication.

But let us consider this example for the sake of illustration. As a Hamming code of

distance d

min

= 3, we have learnt that it has the capability of correcting no more than

min

− 1)/2 = 1 bit errors out of a seven-bit block. If a single error occurs in a block

sequence of 1001 bits (143 blocks), corresponding to BER ≈ 1 × 10

−3

, this error will

be absolutely corrected, with a resulting BER of 0. If, in a block sequence of 2002 bits,

exactly two errors occur within the same block, then only one error will be corrected,

and the corrected BER will be reduced to BER ≈ 0.5 × 10

−3

= 5 × 10

−4

. Since the

condition BER ≈ 0 is not achieved when there is more than one error, this code is,

therefore, not optimal in view of the CCT, despite the fact that it satisﬁes the condition

R < C. Note that the actual corrected error rate (which takes into account all error-event

possibilities) is BER < 4 ×10

−6

, which is signiﬁcantly smaller yet not identical to zero,

and is left as an exercise to show.

262 Channel capacity and coding theorem

Second, the CCT points to the existence of better codes (n, nR) with R < 0.9985 . . . ,

of which (255, 231), with R = 231/255 = 0.905 < C, for instance, is an eligible one.

From Chapter 11, it is recognized as the Reed–Solomon code RS(255, 231) = (n =

− 1, k = n − 2t) with m = 8, t = 12, and code rate R = 231/255 = 0.905 < C. As

we have seen, this RS code is capable of correcting up to t = 12 bit errors per 255-

bit block, yielding, in this case, absolute error correction. Yet the ﬁnite possibility of

getting 13 errors or more within a single block mathematically excludes the possibility

of achieving BER = 0. The probability p(e > 12) of getting more than 12 bit errors in

a single block is given by the formula

p(e > 12) =

255



i−13

255

(1 − ε)

255−i

= p(13) + p(14) +···+p(255),

(13.40)

with (as assumed here) ε = 10

−3

. Retaining only the ﬁrst term p(13) of the expansion

(13 errors exactly), we obtain:

p(13) = C

255

(1 − ε)

255−13

255!

13! 242!

−13×3

(1 − 10

−3

)

242

(13.41)

which, after straightforward computation, yields p(13) ≈ 1.8 × 10

−18

. Because of the

rapid decay of other higher-order probabilities, it is reasonable to assume, without

any tedious proof, that p(e > 12) < 1.0 × 10

−18

, corresponding to an average single-

bit error within one billion billion bits, which means that this RS code, with rate

R = 0.905 < 0.9985 = C, is pretty much adequate for any realistic applications. Yet

there surely exist better codes with rates close to the capacity limit, as we know with

error-correction capabilities arbitrarily close to the BER = 0 absolute limit.

To conclude this chapter, the CCT is a powerful theorem according to which we know

the existence of coding schemes enabling one to send messages through a noisy chan-

nel with arbitrarily small transmission errors. But it is important to note that the CCT

does not provide any indication or clue as to how such codes may look like or should

even be designed! The example code that we have used as a proof of the CCT con-

sists in randomly choosing 2

codewords from the input typical set of size 2

nH(X)

As we have seen, such a code is asymptotically optimal with increasing code lengths

n, since it provides exponentially decreasing transmission errors. However, the code

is impractical, since the corresponding look-up table (y

↔ x

),whichmustbeused

by the decoder, increases in size exponentially. The task of information theorists is,

therefore, to ﬁnd more practical coding schemes. Since the inception of the CCT, sev-

eral families of codes capable of yielding suitably low transmission errors have been

developed, but their asymptotic rates (R = (log M)/n) still do not approach the capacity

limit (C).

13.4 Exercises 263

13.4 Exercises

13.1 (M): Consider the binary erasure channel with input and output PDF,

p(X) = [ p(x

), p(x

)],

P(Y ) = [ p(y

), p(φ), p(y

)],

and the transition matrix,

P(Y |X) =





1 − ε 0

εε

01− ε





Demonstrate the following three relations:

H(Y ) = f (ε) + (1 −ε) f (q),

H(Y |X ) = f (ε),

H(X ; Y ) = H (Y ) − H (Y |X) = (1 − ε) f (q),

where q = p(x

) and the function f (u) is deﬁned as (0 ≤ u ≤ 1):

f (u) =−u log u − (1 −u)log(1− u).

13.2 (M): Determine the bit capacity of a four-input, four-output quaternary chan-

nel with quaternary sources X = Y ={0, 1, 2, 3}, as deﬁned by the following

conditions on conditional probabilities:

p(y|x) =



0.5ify = x ± 1mod4

0 otherwise.

13.3 (T): Determine the capacity of the four-input, eight-output channel characterized

by the following transition matrix:

P(Y |X) =







1001

1100

0110

0011







13.4 (M): Assuming an uncorrected bit-error-rate of BER ≈ 1 ×10

−3

, determine the

corrected BER resulting from implementing the Hamming code (7, 4) in a binary

channel. Is this code optimal in view of the channel coding theorem?

13.5 (B): Evaluate an upper bound for the corrected bit-error-rate when using the

Reed–Solomon code RS(255, 231) over a binary channel with noise parameter

ε = 10

−3

(clue: see text).

14 Gaussian channel and

Shannon–Hartley theorem

This chapter considers the continuous-channel case represented by the Gaussian chan-

nel, namely, a continuous communication channel with Gaussian additive noise. This

will lead to a fundamental application of Shannon’s coding theorem, referred to as the

Shannon–Hartley theorem (SHT), another famous result of information theory, which

also credits the earlier 1920 contribution of Ralph Hartley, who derived what remained

known as the Hartley’s law of communication channels.

This theorem relates channel

capacity to the signal and noise powers, in a most elegant and simple formula. As a

recent and little-noticed development in this ﬁeld, I will describe the nonlinear channel,

where the noise is also a function of the transmitted signal power, owing to channel

nonlinearities (an exclusive feature of certain physical transmission pipes, such as opti-

cal ﬁbers). As we shall see, the modiﬁed SHT accounting for nonlinearity represents

a major conceptual progress in information theory and its applications to optical com-

munications, although its existence and consequences have, so far, been overlooked in

textbooks. This chapter completes our description of classical information theory, as

resting on Shannon’s works and founding theorems. Upon completion, we will then be

equipped to approach the ﬁeld of quantum information theory, which represents the

second part of this series of chapters.

14.1 Gaussian channel

Referring to Chapter 6,acontinuous communications channel assumes a continuous

originator source, X , whose symbol alphabet x

,...,x

can be viewed as representing

time samples of a continuous, real variable x, which is associated with a continuous

probability distribution function or PDF, p(x). The variable x can be conceived as

representing the amplitude of some signal waveform (e.g., electromagnetic, electrical,

optical, radio, acoustical). This leads one to introduce a new parameter, which is the

signal power. This is the power associated with the physical waveform used to propagate

the symbols through a transmission pipe. In any physical communication channel, the

signal power, or more speciﬁcally the average signal power P, represents a practical

Hartley established that, given a peak voltage S and accuracy (noise) S = N , the number of distinguishable

pulses is m = 1 + S/N . Taking the logarithm of this result provides a measure of maximum available

information: this is Hartley’s law. See: http://en.wikipedia.org/wiki/Shannon%E2%80%93Hartley_theorem.

14.1 Gaussian channel 265

constraint, which (as we shall see) must be taken into account to evaluate the channel

capacity.

As a well-known property, the power of a signal waveform with amplitude x is pro-

portional to the square of the amplitude x

. Overlooking the proportionality constant,

the corresponding average power (as averaged over all possible symbols) is, thus, given

P =



p(x)dx =x



. (14.1)

Chapter 6 described the concept and properties of differential entropy, which is the

entropy H (X ) of a continuous source X . It is deﬁned by an integral instead of a discrete

sum as in the discrete channel, according to:

H(X ) =−



p(x)logp(x)dx ≡log p(x)

. (14.2)

As a key result from this chapter, it was established that under the average-power

constraint P, the Gaussian PDF is the one (and the only one) for which the source

entropy H(X ) is maximal. No other continuous source with the same average power

provides greater entropy, or average symbol uncertainty, or mean information contents.

In particular, it was shown that this maximum source entropy, H

max

(X ), reduces to the

simple closed-form expression:

max

(X ) = log

√

2πeσ

, (14.3)

where σ

is the variance of the source PDF.

By sampling the signal waveform, the originating continuous source is actually trans-

formed into a discrete source. Thus the deﬁnition of discrete entropy must be used,

instead of the differential or continuous deﬁnition in Eq. (14.2), but the result turns

out to be strictly identical.

In the following, we will, therefore, consider the Gaussian

As can be shown through the following. Assume the Gaussian PDF for the source X

p(x) =

√

2π

exp



−

2σ



where x is the symbol-waveform amplitude, and σ

=x

=P

is the symbol variance, with P

being the

average symbol or waveform power. By deﬁnition, the source entropy corresponding to discrete samples x

H(X ) =−



p(x

)log

p(x

which can be developed into

H(X ) =−



√

2π

exp

−

2σ

log



2π

−

2σ

log

(e)

≡

log

2πσ



p(x

) +

2σ

log

(e)



p(x

The samples x

can be chosen sufﬁciently close for the following approximations to be valid:



p(x

) = 1,

and



p(x

) =x

=σ

. Finally, we obtain

H(X ) =

log

2πσ

2σ

log

(e) =

log

2πeσ

= log

(

2πeσ

266 Gaussian channel and Shannon–Hartley theorem

channel to be discrete, which allows for considerable simpliﬁcation in the entropy com-

putation. However, I shall develop in footnotes or as exercises the same computations

while using continuous-channel or differential entropy deﬁnitions, and show that the

results are strictly identical. The conclusion from this observation is that there is no need

to assume that the Gaussian channel uses a discrete alphabet or samples of a continuous

source.

The Gaussian channel is deﬁned as a (discrete or continuous) communication channel

that uses a Gaussian-alphabet source as the input, and has an intrinsic additive noise,

also characterized by a noise source Z with Gaussian PDF. The channel noise is said to

be additive, because given the input symbol x (or x

, as sampled at time i ), the output

symbol y (or y

)isgivenbythesum

y = x + z,

= x

+ z

(14.4)

where z (or z

) is the amplitude of the channel noise.

Further, it is assumed that:

(a) The average noise amplitude is zero, i.e., z=0;

(b) The noise power is ﬁnite, with variance σ

=z

=N ;

These three conditions make it possible to calculate the average output power σ

out

of the

Gaussian channel, as follows:

out

=y

=(x + z)

=x

+ 2xz + z



=x

+2xz+z

 (14.5)

= σ

+ σ

≡ P + N ,

where σ

=x

=P is the (average) input signal power. Consistently with the deﬁ-

nition in Eq. (14.3), the entropies of output source Y and the noise source Z are given

by:

H(Y ) = log



(

2πeσ

out



(14.6)

and

H(Z ) = log



(

2πeσ



, (14.7)

respectively.

The mutual information of the Gaussian channel is deﬁned as:

H(X ; Y ) = H (X ) − H (X |Y ) = H (Y ) − H (Y |X), (14.8)

where H (Y |X)istheequivocation or conditional entropy. Given a Gaussian-distributed

variable y = x + z, where x, z are independent, the conditional probability of measuring