Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

14.1 Gaussian channel 267

y at the output given that x is the input is p(y|x) = p(z). Substituting this property in

the deﬁnition of conditional entropy H(Y |X ), we obtain:

H(Y |X ) =−



p(x

, y

)logp(y

)

=−



p(y

)p(y

)logp(y

)

=−



p(y

)p(z

)logp(z

) (14.9)

=−



p(y

)



p(z

)logp(z

)

= H (Z)

= log

(

2πeσ

As previously stated, the same result as in Eq. (14.9) can be obtained using the differential

or continuous deﬁnition of conditional entropy, i.e., to recall from Chapter 6:

H(Y |X ) =−



p(y|x) p(x)logp(y|x)dxdy. (14.10)

The computation of the double integral in Eq. (14.10) is elementary, albeit relatively

tedious to carry out, so we shall leave it here as a “math” exercise.

We consider next the capacity of the Gaussian channel. By deﬁnition, the channel

capacity C is given by the maximum of the mutual information H (X; Y ) = H (Y ) −

H(Y |X ). Using the previous results in Eqs. (14.6) and (14.7)forH (Y ) and H (Y |X) =

H(Z ), we obtain:

H(X ; Y ) = H(Y ) − H(Y |X ) = H (Y ) − H(Z )

log



πeσ

out



−

log



2πeσ



log



out



log



+ σ



(14.11)

and using σ

out

= σ

+ σ

, σ

= P, σ

= N :

H(X ; Y ) =

log



1 +



. (14.12)

The mutual information H (X ; Y ) deﬁned in Eq. (14.12) also corresponds to the channel

capacity C. This is because (given the signal power constraint P) the Gaussian distribu-

tion maximizes the source entropies H (X )orH(Y ), making H (X; Y ) an upper bound

for mutual information. Thus, we can write, equivalently:

C =

log



1 +



. (14.13)

In the above, the quantity P/N is called the signal-to-noise ratio, or SNR. The funda-

mental result in Eq. (14.13), which establishes that the capacity of a “noisy channel”

is proportional to log(1 + SNR) is probably the most well known and encompassing

268 Gaussian channel and Shannon–Hartley theorem

Hypersphere surface

(a)

(b)

(

)

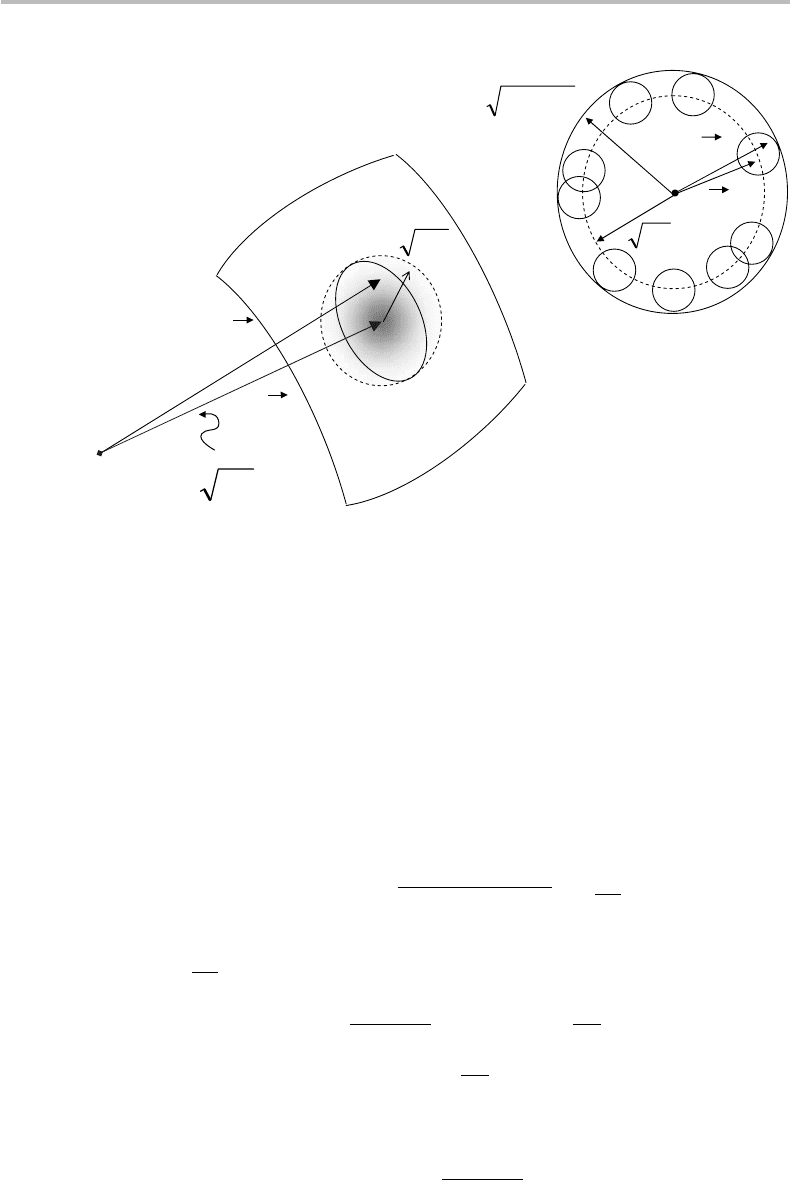
Figure 14.1 (a) Location of input message x, deﬁned by vector x, and likely location of output

message y, deﬁned by vector y, on the surface of a hypersphere of dimension n; (b) as (a), but

for n = 2.

conclusion of all Shannon’s information theory. Given the SNR characteristics of a com-

munication channel with noise and signal power limitation, it provides an upper bound

for the code rate at which information can be transmitted with arbitrarily small errors.

Before expanding on the implications of this result for communication systems, it is

worth providing a plausibility argument for the existence of the corresponding codes

with low error probability. The argument immediately following can be found with

different variants in most IT textbooks.

Consider an input message (or codeword) consisting of a sequence of n discrete

waveform samples with random amplitudes x

of zero mean and mean power x

=P.

This message deﬁnes a vector x = (x

, x

,...,x

)inann-dimensional space, which

is characterized by a length | x|=

(

+ x

+···+x

√

nP. Thus, we can view

the input message as lying on any point x = (x

, x

,...,x

), which is most probably

located close to the surface of a hypersphere centered about the origin and having a

radius of

√

nP. Likewise, the received or output message corresponds to an n-vector

y = (y

, y

,...,y

) with y

= x

+ z

, where z

=0 and z

=N . Thus, the output

vector y has the length | y|=



n(P + N ) with deviation

√

nN. The output message is

likely to fall on any point y = (y

, y

,...,y

) inside a small hypersphere centered about

x = (x

, x

,...,x

) and having a radius of

√

nN, as illustrated in Fig. 14.1.

For any output message y to represent nonconfusable input messages x (i.e., most

likely to correspond to a unique input message x), the small spheres should be nonin-

tersecting or disjoint. Here comes the key question: how many such disjoint spheres can

be ﬁtted inside the hypersphere of radius



n(P + N )?

14.1 Gaussian channel 269

The answer comes as follows. The volume V

of a hypersphere with dimension n and

radius r is given by the formula V

= A

, with the coefﬁcient A

deﬁned by:

n/2





1 +



, (14.14)

where (m) is the gamma function.

The maximum number M of disjoint spheres that

can be ﬁtted inside the volume V

is, thus,

M =





n(P + N )





√





1 +



n/2

≡ 2

log

(1+

)

. (14.15)

The result in Eq. (14.15) shows that there exist M = 2

possible messages with non-

confusable inputs, corresponding to the channel or code rate

R =

log



1 +



. (14.16)

Since R is the maximum rate for which the messages have nonconfusable inputs (mean-

ing that receiving and decoding errors can be made arbitrarily small), the value found

in Eq. (14.16) represents an upper bound, which corresponds to the channel capacity.

Thus, the demonstration conﬁrms the fundamental result found in Eq. (14.13).

The unit of channel capacity is bits or, more accurately, bits per channel use.

Then how

does channel capacity relate to channel bandwidth? We shall now address this question

as follows. Deﬁne B as the signal bit rate. To recover bits from signal waveforms, a basic

engineering principle states that the waveform must be sampled at the Nyquist sampling

rate of f = 2B per unit time (i.e., twice the bit rate). A continuous communication

channel with a capacity C

bit

, which is used at the rate f = 2B, gives us the capacity per

unit time C

bit/s

= 2BC

bit

Substituting the above result into Eq. (14.13), we obtain

bit/s

= B log



1 +



. (14.17)

By dividing both sides in Eq. (14.17)byB, we obtain another deﬁnition of channel

capacity, which now has the dimensionless unit of (bit/s)/Hz:

(bit/s)/Hz

= log



1 +



. (14.18)

The results in either Eq. (14.17)orEq.(14.18) are known as the Shannon–Hartley the-

orem (SHT), based on an earlier contribution from Hartley to Shannon’s analysis (see

previously). The SHT is also referred to as the Shannon–Hartley law,theinformation

The gamma function has the property (m + 1) = m!, with (1/2) =

√

π, (3/2) =

√

π/2, and (m +

1/2) = (1/2)

1.3.5,...,(2m−1)

. It can readily be checked that V

= A

with the deﬁnition in Eq. (14.14)

yields V

= πr

, V

= (4/3)πr

, etc.

Channel capacity is conceptually similar to the capacity of transportation means. Thus, if for instance an

airplane or a truck can transport 300 passengers or 20 tons, respectively, this corresponds to capacities of

300 passengers or 20 tons per single use of the airplane or of the truck. Using these transportation means

several times does not increase the capacity per use, as was also shown in Appendix L.

270 Gaussian channel and Shannon–Hartley theorem

capacity theorem,ortheband-limited capacity theorem. To recall, SHT or its different

appellations relate to Shannon’s “second theorem” or “[noisy] channel-capacity theo-

rem.” As expressed in Eq. (14.17), the SHT provides the maximum bit rate achievable

bit/s

) given the channel bandwidth, additive noise background, and signal power con-

straint, for which information can be transmitted with an arbitrarily small BER.The

SHT variant in Eq. (14.18) provides the maximum bit rate achievable per unit of band-

width (Hz), under said conditions. The bit rate normalized to bandwidth is referred to as

information spectral density, or ISD. The (bit/s)/Hz ISD, is often referred to as spectral

efﬁciency. This would be a correct appellation if the ISD was bounded to a maximum

of unity, corresponding to 100% efﬁciency, or 1 (bit/s)/Hz. However, there are a variety

of modulation formats, which make it possible to encode more than 1 bit/s in a single

Hz of frequency spectrum, as discussed further on. Regardless of the possible existence

of such modulation formats, the SHT states that the ISD is actually unbounded.In

the limit of high signal-to-noise ratios (SNR = P/N ), we ﬁnd C ≈ log

(SNR). This

result means that every twofold increase (or 3 dB, in the decibel scale

) of the SNR

corresponds to an ISD increase of one additional (bit/s)/Hz. For instance, SNR = 2

1024 =+30.1 dB corresponds to an ISD of log

(1 + 2

) ≈ 10 (bit/s)/Hz. The SHT,

thus, states that given any SNR constraint, there exist some codes (and associated

modulation formats) for which error-free transmission is possible within an ISD limit

of C

(bit/s)/Hz

= log

(1 + SNR). As with the (discrete) channel coding theorem (Chapter

13), how to ﬁnd or to design such codes is, however, not speciﬁed by the theory.

In the above SHT formulation, it is possible to introduce another important parameter

overlooked so far, which is the noise bandwidth. Assume a communication channel with

a capacity per unit time of C

bit/s

and a signal bandwidth B. The mean signal power, P,

and the mean energy per bit, E

, are related through P = E

bit/s

. The noise power, N ,

and the mean noise energy per bit, E

, are related through N = E

. Thus, the SNR

can also be expressed in the form

SNR =

bit/s

, (14.19)

which explicitly relates the bit SNR to the bandwidth B. Replacing the above result in

Eq. (14.17) yields

bit/s

= B log



1 +

bit/s



, (14.20)

then

bit/s

= log



1 +

(bit/s)/Hz



. (14.21)

For any nonnegative real number q

linear

, the decibel scale is deﬁned as q

= 10 log

linear

). For instance,

20 dB = 100

linear

, −10 dB = 0.1

linear

, and, in particular, 3.0102 dB ≈ 3dB= 2

linear

14.1 Gaussian channel 271

0 5 10 15 20

SNR

bit

(dB)

ISD ((Bit/s)/Hz)

0.01

0.1

−5

−1.6 dB

Shannon limit

Figure 14.2 Bandwidth-efﬁciency diagram plotting information spectral density (ISD) vs.

signal-to-noise ratio (bit SNR), according to Eq. (14.22). The two regions R < C and R > C,

corresponding to bit rate R and channel capacity C

bit/s

, which are separated by the capacity-

boundary curve (R = C) are also shown. The Shannon limit corresponds to SNR =−1.6 dB.

Base-two exponentiation of both sides of Eq. (14.21), and the introduction of SNR

bit

as deﬁning the bit SNR,

we ﬁnally obtain:

SNR

bit

(bit/s)/Hz

− 1

(bit/s)/Hz

. (14.22)

This formula now provides an explicit and universal relation between the bit SNR

(SNR

bit

) and the channel ISD (C

(bit/s)/Hz

). It is, thus, possible to plot the function

(bit/s)/Hz

= f (SNR

bit

), as shown in Fig. 14.2, which is referred to as the bandwidth-

efﬁciency diagram.

As observed from Fig. 14.2, the boundary curve C

(bit/s/Hz)

= f (SNR

bit

) deﬁnes two

regions in the plane. If R

bit/s

is the bit rate, these two regions correspond to R

bit/s

< C

bit/s

and R

bit/s

> C

bit/s

, respectively. The interpretation of the bandwidth-efﬁciency diagram

is then:

In the region R

bit/s

< C

bit/s

, there exist codes for which transmission can be achieved

with arbitrary low error (BER);

In the region R

bit/s

> C

bit/s

, there is no code making transmission possible at arbitrarily

low error.

To avoid any misinterpretation, it is always possible to transmit information with some

ﬁnite or nonzero BER in any location of the diagram. However, only in the lower-right

region R

bit/s

< C

bit/s

of the diagram can the BER be made arbitrarily small with a proper

code choice code, leading to arbitrarily error-free transmission.

The ratio SNR

bit

= E

is often referred to in textbooks as E

,whereE

= E

is the bit energy and

= E

is the noise energy or noise spectral density.

272 Gaussian channel and Shannon–Hartley theorem

We also observe from Fig. 14.2 that the boundary curve C

(bit/s)/Hz

= f (SNR

bit

) has an

asymptotic limit at SNR

bit

=−1.6 dB, which is referred to as the Shannon limit.Asthe

ﬁgure indicates, when the SNR approaches this lower bound, the ISD rapidly vanishes

to become asymptotically zero as SNR

bit

→−1.6 dB. On the right-hand side of the

boundary curve, there exist some codes for which error-free transmission is possible.

But as observed from the ﬁgure, the closer one approaches the Shannon-limit SNR, the

lower the ISD and the smaller the number of bits that can be effectively transmitted per

unit time and unit bandwidth. The limiting condition SNR

bit

=−1.6 dB corresponds to

a useless channel with an ISD of 0 (bit/s)/Hz.

The bandwidth-efﬁciency diagram suggests two strategies for optimizing the trans-

mission of information:

Horizontally, or at ﬁxed ISD, by increasing the bit-SNR to reduce the BER;

Vertically, or at ﬁxed SNR, to increase the ISD and, hence, to increase the bit rate.

At this point, we, thus, need to address two issues: (a) the relation between the waveform

modulation format and the ISD, and (b) for a given modulation format, the relation

between SNR and BER (or symbol error rate, SER, for multi-level formats). With such

knowledge, we will then be able to ﬁll out the diagram with different families of points,

i.e., to plot iso-format or iso-SER/BER curves, and observe the corresponding tradeoffs.

An overview of the different types of modulation formats is beyond the scope of this

book. Here, we shall use a limited selection of modulation formats and their ISD, SNR,

or SER properties to provide illustrative cases of bandwidth-efﬁciency tradeoffs. The

following assumes some familiarity with telecommunications signaling (i.e., intensity,

frequency, phase, amplitude, and multi-level waveform modulation).

Nonreturn-to-zero (NRZ) format

The nonreturn-to-zero (NRZ) format, also called on–off keying (OOK), corresponds to

the most basic and common modulation scheme. Bit encoding consists of turning the

signal power on or off during each bit period, to represent 1 or 0, respectively. Its ISD is

intrinsically limited to 1 (bit/s)/Hz

and its BER is given by the generic formula:

BER =

erfc

SNR

bit

, (14.23)

where erf(x)isthecomplementary error function.

S. Haykin, Digital Communications (New York: J. Wiley & Sons, 1988), J. G. Proakis, Digital Communica-

tions, 4th edn. (New York: McGraw Hill, 2001).

Actually, the 1 (bit/s)/Hz ISD for NRZ/OOK signals represents the asymptotic limit of channel capacity,

which is rapidly reached for SNR

bit

≥ 5 dB. The demonstration of such a result is left as an exercise.

By deﬁnition, erfc(x) = 1 −erf(x) with erf (x) =

√

−y

dy being the error function. The latter can

be approximated through the expansion: erf (x ) = 1 −(a

t + a

+ a

) exp(−x

), with

t = 1/(1 + px), p = 0.3275, a

= 0.2548, a

=−0.2844, a

= 1.4214, a

=−1.4531 and a

= 1.0614.

Consistently with the exact deﬁnition, in the limit x → 0wehaveerf(x) = 0. It is customary to deﬁne

Q =

√

SNR

bit

, hence from Eq. (14.23), BER = erfc(Q/

√

2)/2 with erfc(x) = 1 − erf(x). For Q > 2,

14.1 Gaussian channel 273

−10

−8

−6

−4

−2

−10 −50510 252015

SNR

bit

(dB)

log

BER

BER = 10

−

21.6 dB

Shannon limit

−

1.6 dB

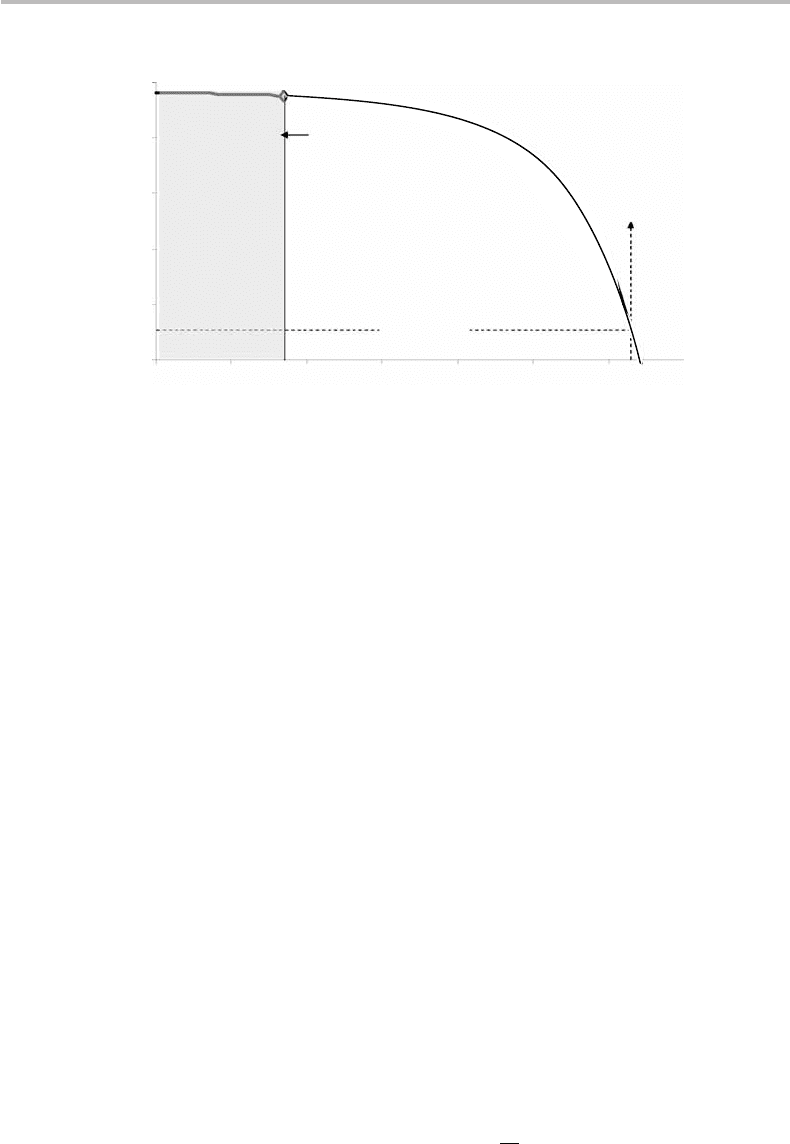
Figure 14.3 Bit error rate (BER) as a function of bit signal-to-noise ratio (SNR

bit

) for NRZ- or

OOK-modulated signals.

Figure 14.3 shows the plot BER = f (SNR

bit

), along with the Shannon limit. It is

seen from the ﬁgure that the speciﬁc value SNR

bit

=+21.6 dB yields a BER of 10

−9

corresponding to one bit error (on average) for every one billion bits transmitted. For

a long time in the modern history of telecommunications, such a BER has been con-

sidered to represent the standard for “error-free” transmission. In the limit of vanishing

signals, or SNR

bit

→ 0orSNR

bit

(dB) →−∞, the erf function vanishes and we have

BER = 1/2. Since the BER is a probability, this result means that the bits 0 and 1 have

equal probabilities of being detected, regardless of the input message sequence, which

corresponds to a useless communication channel.

The shaded region in Fig. 14.3 deﬁnes the impossibility of ﬁnding error-correction

codes (ECC) able to improve the BER at a given SNR

bit

value, while right-hand side

region indicates that the possibility exists. A detailed introduction to the subject of ECC

is provided in Chapter 11. Here, I shall provide a heuristic example illustrating the actual

effect of error correction on the (otherwise uncorrected) BER performance.

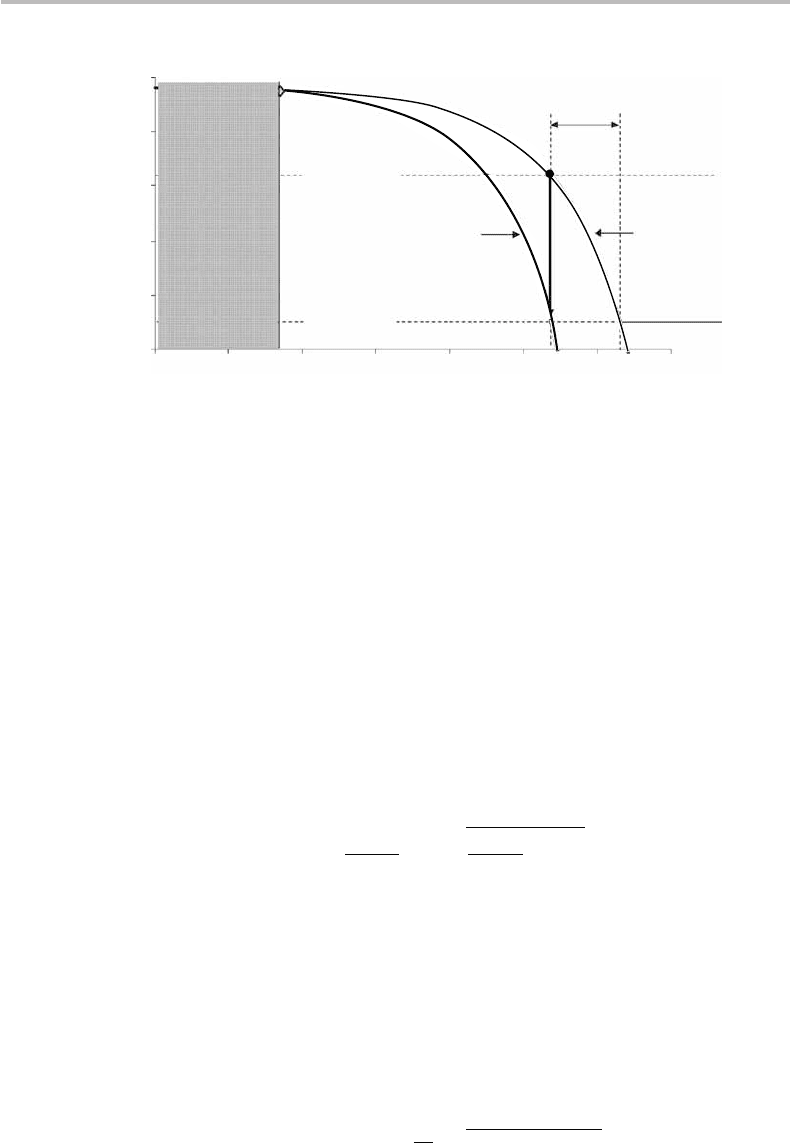
Figure 14.4 shows an example of ECC implementation where the physically achiev-

able signal-to-noise ratio is SNR

bit

= 16.6 dB. At the receiver level, and before error-

correction decoding, the bit error rate is about BER = 10

−3.5

. After correction, the

bit error rate is seen to improve BER = 10

−9

. As the ﬁgure indicates, the horizontal

translation between the two BER curves (uncorrected on top, and corrected at bottom)

corresponds to a virtual, but effective SNR shift of +5 dB. As formally described in

Chapter 11, this SNR shift is referred to as the coding gain.

the BER can be approximated by BER = exp(−Q

/2)/(Q

√

2π), which yields BER = 10

−9

for Q = 6or

SNR

bit

= 4Q

= 144 =+21.58 dB. Note that different SNR deﬁnitions apply to optical telecommunication

systems. A standard deﬁnition is SNR ≈ Q

, which gives SNR ≈+15.5 dB for BER = 10

−9

274 Gaussian channel and Shannon–Hartley theorem

−2

−4

−6

−8

−10

−10 −50510152025

Before

correction

SNR

bit

(dB)

log

BER

−

Coding gain

5 dB

After

correction

Operating

SNR

16.6 dB

BER

−

3.5

Figure 14.4 Illustration of the effect of error-correction coding (ECC) on the BER performance

(NRZ/OOK), showing a coding gain of +5 dB improving the BER from BER =10

−3.5

to BER =

−9

-ary frequency-shift-keying (

-FSK) format

The M-ary frequency-shift-keying (M-FSK) format is based on multi-level frequency

modulation, where M is a power of two, and coherent detection. The ISD asso-

ciated with M-ary FSK modulation is given by ISD = (2 log

M)/M. Hence, for

M = 2, 4, 8, 16, 32, 64, 128 we have ISD = 1, 1, 0.75, 0.5, 0.31, 0.18, 0.1 (bit/s)/Hz,

respectively. The ISD, thus, decreases as the number of modulation levels M increases,

which is a drawback speciﬁc to this modulation format, which is not bandwidth efﬁcient.

The symbol error rate (SER) of M-FSK signals is given by the following approximation

(valid for SER ≤ 10

−3

SER ≈

M − 1

erfc

SNR

bit

log

. (14.24)

-ary phase-shift-keying (

-PSK) format

The M-ary phase-shift-keying (M-PSK) format is based on multi-level phase modula-

tion. Like M-FSK, it requires coherent detection. The ISD associated with M-ary PSK

modulation is given by ISD = log

M, which shows that it increases with M. Hence,

for M = 2, 4, 8, 16, 32, 64, 128 we have ISD = 1, 2, 3, 4, 5, 6, 7 (bit/s)/Hz, respectively.

The SER of M-PSK signals is given by:

SER = erfc



sin



SNR

bit

× log



. (14.25)

14.1 Gaussian channel 275

-ary quadrature amplitude modulation (

-QAM) format

The M-ary quadrature amplitude modulation (M-QAM) format is based on coherent

multi-level amplitude modulation, using the combination of two quadratures.

As in

the previous case, the ISD associated with M-ary QAM modulation is ISD = log

The SER of M-QAM signals is given by:

SER = 2



1 −

√



erfc

3SNR

bit



2(M − 1)

log

, (14.26)

where SNR

bit

 represents the average bit SNR. This averaging is required because

the waveform energy depends on the particular symbol being transmitted, unlike the

previous modulation formats.

Using Eqs. (14.23)–(14.26), and the numerical approximation for erfc(x), one can

compute the SER associated with each modulation format for different values of M.

Since we are interested in iso-SER plots, we may choose, for instance, SER = 10

−3

−5

,10

−11

for each of these plots and ﬁnd the corresponding SNR

bit

values numerically

in each case.

The result is shown in Fig. 14.5.

One observes from the ﬁgure that

there exist qualitative differences between the different formats. Comparing ﬁrst binary

formats (M =2, SER ≡ BER), it is seen that at equal BERs, NRZ requires substantially

higher SNRs than any other format. This feature is explained by the fact that the other

formats use coherent receivers, which have higher sensitivity: for equal SNRs, coherent

receivers yield lower BERs than the direct-detection receivers used in NRZ. All binary

formats have an ISD of 1 (bit/s)/Hz.

Therefore, the only two degrees of freedom are

the format and the BER. Binary QAM is seen to have the lowest SNR requirement at

given BER. The choice of a modulation format being primarily dictated by practical

engineering considerations (complexity of transmitter or receiver, feasibility, reliability,

cost), the BER is not necessarily a decisive factor. Furthermore, we know from the

SHT that for any SNR satisfying SNR

bit

> −1.6 dB, there exist (error-correction) codes

making it possible to reduce the BER to arbitrarily small values. How practical such

codes are to implement, and how powerful (coding gain) remain two key questions for

system design.

Consider next the M-ary format plots shown in Fig. 14.5. An additional degree

of freedom is provided by the number of modulation levels, M, which makes it

possible to modify the ISD. As previously seen, M-FSK is not bandwidth-efﬁcient

The modulated signal has the form f (t) = a(t)cos(ωt) +b(t )sin(ωt), where a(t ), b(t) are independently

modulated with M levels, forming a set of M

coding possibilities or constellations.

This computation can be simply achieved by using a computer spreadsheet to tabulate the SER vs. SNR

functions, and then by ﬁnding the SNRs corresponding to the three reference SERs.

Figure originally published in E. Desurvire, Survival Guides Series in Global Telecommunications, Sig-

naling Principles, Network Protocols and Wireless Systems (New York: J. Wiley & Sons, 2004). See also

S. Haykin, Digital Communications (New York: J. Wiley & Sons, 1988), J. G. Proakis, Digital Communi-

cations, 4th edn. (New York: McGraw Hill, 2001) for other data points.

A note at the end of this chapter shows that the capacity is asymptotically C → 1 bit for increasing SNRs;

convergence is rapid, thus the approximation C ≈ 1 bit is valid for SNRs greater than 5 dB.

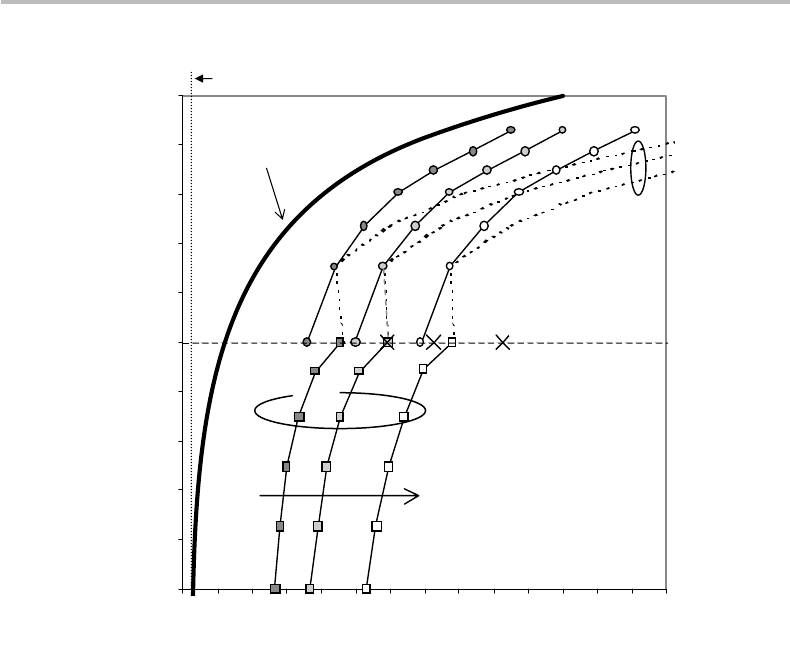
276 Gaussian channel and Shannon–Hartley theorem

−1

0.8

0.6

0.4

0.2

−0.2

−0.4

−0.6

−0.8

−2 0 2 4 6 8 10 12 14 16 18 20 22 24 26

Bit SNR (dB)

128

FS K

PS K

QAM

BER

=10

-3

to 10

-11

SHT boundary

Information spectral density ((bit/s)/Hz)

bit SNR (dB)

FSK

PSK

QAM

SER = 10

−3

to 10

−11

NRZ

Shannon limit

Figure 14.5 Bandwidth-efﬁciency diagram showing (bit/s)/Hz ISD (in log

) as a function of bit

SNR (in dB) for different coherent M-ary modulation formats, M-QAM, M-PSK, and M-FSK,

and for error rates of SER = 10

−3

(dark symbols), SER = 10

−5

(shaded symbols), and SER =

−11

(open symbols). For clarity, the symbols are not shown for M-PSK (the ISD being identical

to that of QAM for each M). The crosses (×) on the horizontal axis correspond to NRZ/OOK

modulation for BER = 10

−3

,10

−5

,10

−11

and multi-level modulation decreases the ISD: a 128-FSK format has an ISD of 0.1

(bit/s)/Hz, which is ten times less than NRZ. Compared with M-QAM and M-PSK,

however, M-FSK is seen to have a lower SNR requirement for a given BER, but this

advantage does not compensate for the large bandwidth inefﬁciency. It is also note-

worthy that the M-FSK iso-SER curves move away from the SHT boundary as M

increases.

Focusing now on M-QAM and M-PSK, we observe from the ﬁgure that increasing ISD

(though increasing M) requires higher SNRs. The SNR requirement increases far more

rapidly with M-PSK. For instance, at SER = 10

−3

, the formats 64-PSK and 64-QAM

approximately require SNR = 26 dB and SNR = 15 dB, respectively, corresponding to

an SNR difference of more than 10 dB. From this analysis, M-QAM appears to be the

champion format in combined terms of ISD and SNR requirements. It is noteworthy

that as M is increases, the iso-SER curves of M-QAM and M-PSK move closer to

the SHT boundary, contrary to M-FSK. The closer any point in these curves get to