Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

13.1 Channel capacity 247

1.0

Parameter

0.3

0.4

0.5

0.6

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

Parameter

Probability

0.05

0.95

0.99

0.01

= 0.5

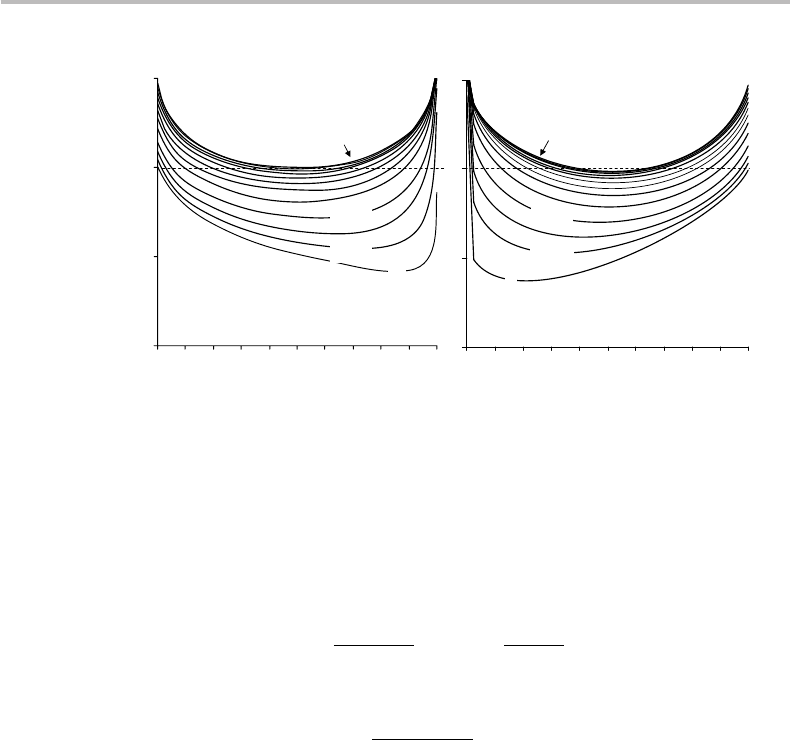
Figure 13.1 Optimal input probability distribution q = p(x

) = 1 − p(x

), corresponding to

capacity C of binary channel, plotted as a function of the two transition-matrix parameters a and

b (step of 0.05).

The demonstration of the above result, which is elementary but far from straightfor-

ward, is provided in Appendix K. This Appendix also shows that the corresponding

optimal distribution is given by p(x

) = q, p(x

) = 1 − q with the parameter q deﬁned

according to:

q =

a + b − 1



b −1 +

1 + 2



, (13.9)

with

W =

f (a) − f (b)

a + b − 1

= V − U. (13.10)

It is straightforward to verify that in the case a = b = 1 −ε (binary symmetric channel),

the channel capacity deﬁned in Eqs. (13.7)–(13.8) reduces to C = 1 − f (ε) and the

optimal input distribution reduces to the uniform distribution p(x

) = p(x

) = q = 1/2.

The case a + b = 1, which seemingly corresponds to a pole in the above deﬁnitions,

is trickier to analyze. Appendix K demonstrates that the functions U, V, W , and q

are all continuously deﬁned in the limit a + b → 1 (or for that matter, over the full

plane a, b ∈ [0, 1]). In the limit a + b → 1, it is shown that H (Y ; X ) = C = 0, which

corresponds to the case of the useless channel. The fact that we also ﬁnd, in this case,

q = 1/2 (uniform input distribution) is only a consequence of the continuity of the

function q. As a matter of fact, there is no optimal input distribution in useless channels,

and all possible input distributions yield C = 0.

Figures 13.1 and 13.2 show 2D and 3D plots of the probability q = p(x

) = 1 − p(x

)

as a function of the transition-matrix parameters a, b ∈ [0, 1] (sampled in steps of 0.05),

as deﬁned from Eqs. (13.9) and (13.10). It is seen from the ﬁgures that the optimal input

probability distribution is typically nonuniform.

The 3D curve shows that the optimal

Yet for each value of the parameter b, there exist two uniform distribution solutions, except at the point

a = b = 0.5, where the solution is unique (q = 1/2).

248 Channel capacity and coding theorem

Parameter

0.6

0.5

Distribution

(

) = 1 −

(

)

0.4

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 13.2 3D representation of the data shown in Fig. 3.1..

distribution has a saddle point at a = b = 1/2, which, as we have seen earlier, is one

case of a useless channel (a + b = 1).

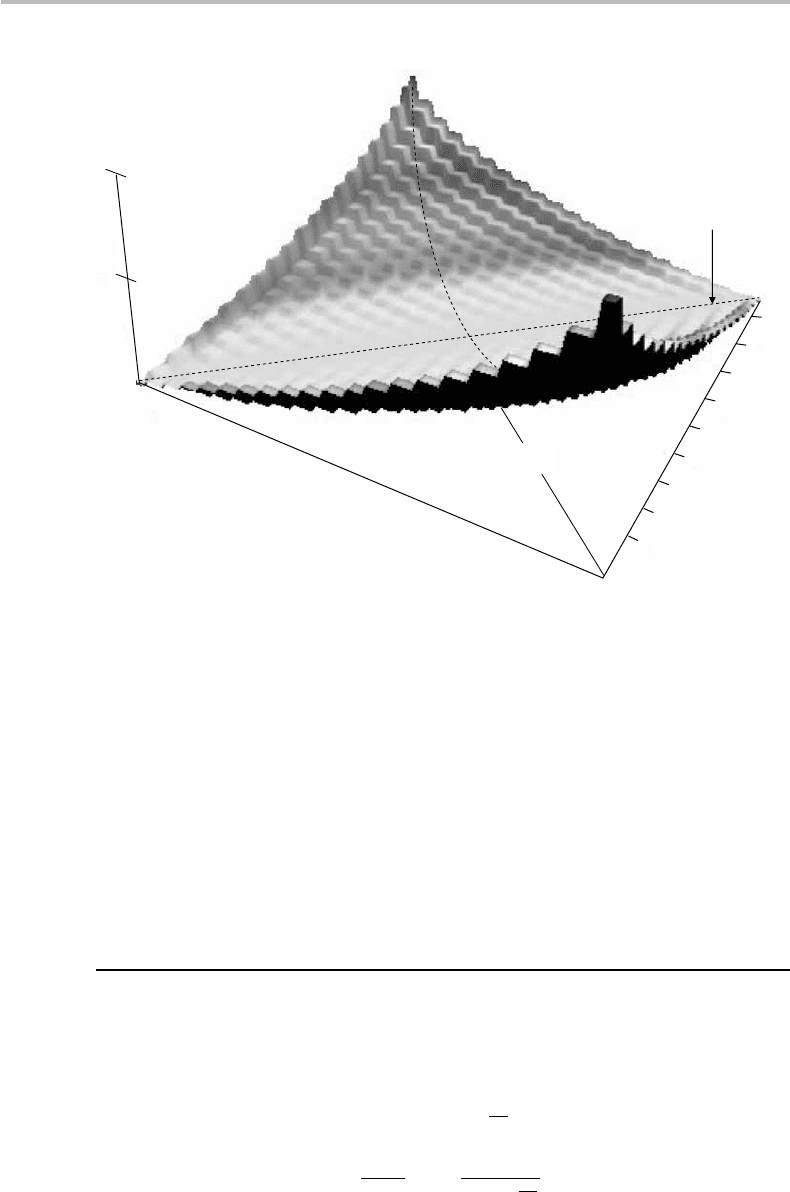
Figure 13.3 shows the corresponding 3D surface plot of the channel capacity C,as

deﬁned in Eqs. (13.7) and (13.8). It can be observed from the ﬁgure that the channel-

capacity surface is symmetrically folded about the a + b = 1 axis, along which C = 0

(useless channel). The two maxima C = 1 located in the back and front of the ﬁgure

correspond to the cases a = b = 0 and a = b = 1, which deﬁne the transition matrices:

P(Y |X) =









, (13.11)

respectively. These two matrices deﬁne the two possible noiseless channels, for which

there exists a one-to-one correspondence between the input and output symbols with

100% certainty.

Since there is no reason to have a one-to-one correspondence between the symbols or indices, we can also

have p(y

) = 1fori = j and p(y

) = 0fori = j. Thus, a perfect binary symmetric channel can

equivalently have either of the transition matrixes (see deﬁnition in text):

P(Y |X) =





P(Y |X) =





Since in the binary system, bit parity (which of the 1 or 0 received bits represents the actual 0 in a given

code) is a matter of convention, the noiseless channel can be seen as having an identity transition matrix.

13.1 Channel capacity 249

0.5

1.0

Parameter

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

= 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Channel

capacity

Figure 13.3 Binary channel capacity C as a function of the two transition-matrix parameters a

and b. The diagonal line a + b = 1 corresponds to the useless-channel capacity C = 0. The

diagonal line a = b corresponds to the binary symmetric-channel capacity C = 1 − f (a).

The other diagonal line in Fig. 13.3 represents the channel capacities for which a = b

corresponds to the binary symmetric channel. Substitution of b = a in Eq. (13.8) yields

U = V =−f (a) and, thus, C = 1 − f (a) from Eq. (13.7, which is the result obtained

earlier in Eq. (13.5). We also obtain from Eq. (13.10) W = 0, and, from Eq. (13.9),

q = 1/2, which is the uniform distribution, as expected from the analysis made in

Chapter 12.

To provide illustrations of channel capacity, we shall consider next the four discrete-

channel examples described in Chapter 12. As usual, the input probability distribution

is deﬁned by the single parameter q = p(x

) = 1 − p(x

Example 13.1: Z channel

The transition matrix is shown in Eq. (12.5), to which the parameters a = 1 and b = 1 −ε

correspond. It is easily obtained from the above deﬁnitions that U = 0 and V = W =

− f (ε)/(1 −ε), which gives

C = log

1 + 2

−

f (ε)

1−ε

, (13.12)

q =

1 − ε



ε +

1 + 2

−

f (ε)

1−ε



. (13.13)

250 Channel capacity and coding theorem

The case ε = 0, for which a = b = 1, corresponds to the noiseless channel with identity

transition matrix, for which C = 1 and q = 1/2. The limiting case ε → 1(a = 1 and

b = 0) falls into the category of useless channels for which a + b = 1, with C = 0

and q = 1/2 (the latter only representing a continuity solution,

but not the optimal

distribution, as discussed at the end of Appendix K).

Example 13.2: Binary erasure channel

The transition matrix is shown in Eq. (12.6). One must then calculate the entropies

H(Y ) and H(Y |X), according to the method illustrated in Appendix K (see Eqs.

(K4)–(K5) and (K7)–(K8)). It is left to the reader as an easy exercise to show that

H(Y ) = f (ε) +(1 −ε) f (q) and H (Y |X) = f (ε). The mutual information is, thus,

H(X ; Y ) = H (Y ) − H(Y |X ) = (1 −ε) f (q) and it is maximal for q = 1/2(df /dq =

[log(1 −q)/q]). Substituting this result into H(X ; Y ) yields the channel capacity

C = 1 −ε. The number 1 − ε = p(y

) = p(y

) corresponds to the fraction of

bits that are successfully transmitted through the channel (a fraction ε being erased).

The conclusion is that the binary-erasure channel capacity is reached with the uniform

distribution as input, and it is equal to the fraction of nonerased bits.

Example 13.3: Noisy typewriter

The transition matrix is shown in Eq. (12.7) for the simpliﬁed case of a six-character

alphabet. Referring back to Fig. 12.4, we observe that each of the output characters,

y = A, B, C,...,Z, is characterized by three nonzero conditional probabilities, e.g., for

y = B: p(B|A) = p(B|B) = p(B|C) = 1/3. The corresponding probability is:

p(y = B) = p(B|A) p(A) + p(B|B) p(B) + p(B|C) p(C)

= [ p(A) + p(B) + p(C)]/3.

(13.14)

The joint probabilities are







p(B, A) = p(B|A)p(A) = p(A)/3

p(B, B) = p(B|B)p(B) = p(B)/3

p(B, C) = p(B|C)p(C) = p(C)/3.

(13.15)

Using the above deﬁnitions, we obtain

H(Y ) =−



p(y

)logp(y

)

=−

p(A) + p(B) + p(C)

log

p(A) + p(B) + p(C)

+↔,

(13.16)

As shown in Appendix K, the continuity of the solutions C and q stems from the limit 1/(1 +2

) ≈

a − η/2, where a + b = 1 −η and η → 0. This limit yields q = 1/2, regardless of the value of a,and

C =−log(a) → 0fora → 1

13.1 Channel capacity 251

where the sign ↔means all possible circular permutations of the character triplets (i.e.,

BCD,DEF,...,XYZ,YZA).Themutualinformationisgivenby:

H(Y |X ) =−



p(x

, y

)logp(y

)

=−[p(B, A) log p(B|A) + p(B, B) log p(B|B) + p(B, C) log p(B|C) ↔]

=−



p(A) + p(B) + p(C)

log

+↔



=−3

p(A) + p(B) +···+p(Z)

log

= log 3. (13.17)

The channel capacity is, therefore:

C = max

p(x)

{

H(Y ) − H (Y |X)

}

= max

p(x)



−

p(A) + p(B) + p(C)

log

p(A) + p(B) + p(C)

+↔

−log 3. (13.18)

The expression between brackets is maximized when for each character triplet, A, B, C,

we have p(A) = p(B) = p(C), which yields the optimal input distribution p(x) = 1/26.

Thus, Eq. (13.18) becomes

C =−



log

+↔

−log 3

log

−log 3

= log 26−log 3

= log

(13.19)

This result could have been obtained intuitively by considering that there exist 26/3

triplets of output characters that correspond to a unique input character.

Thus 26/3

symbols can effectively be transmitted without errors as if the channel were noiseless.

The fact that 26/3 is not an integer does not change this conclusion (an alphabet of 27

characters would yield exactly nine error-free symbols).

Example 13.4: Asymmetric channel with nonoverlapping outputs

The transition matrix is shown in Eq. (12.8). Since there is only one nonzero element

in each row of the matrix, each output symbol corresponds to a single input symbol.

This channel represents another case of the noisy typewriter (Example 3), but with

Namely, outputs Z, A, B uniquely correspond to A as input, outputs C, D, E uniquely correspond to D as

input, etc. Such outputs are referred to as “nonconfusable” subsets.

252 Channel capacity and coding theorem

nonoverlapping outputs. Furthermore, we can write

p(y

or y

) ≡ p(y

) + p(y

)

= p(y

)p(x

) + p(y

)p(x

) + p(y

)p(x

) + p(y

)p(x

)

[

p(x

) + p(x

)

]

≡

= p(y

or y

(13.20)

Deﬁne the new output symbols z

= y

or y

, z

= y

or y

. It is easily established

that the conditional probabilities satisfy p(z

) = p(z

) = 1/2. The corresponding

transition matrix is, thus, the identity matrix. This noisy channel is, therefore, equivalent

to a noiseless channel, for which C = 1 with the uniform distribution as the optimal

input distribution. This conclusion can also be reached by going through the same formal

calculations and capacity optimization as in Example 3.

With the above examples, the maximization problem of obtaining the channel capacity

and the corresponding optimal input probability distribution is seen to be relatively

simple. But one should not hastily conclude that this applies to the general case! Rather,

the solution of this problem, should such a solution exist and be unique, is generally

complex and nontrivial. It must be found through numerical methods using nonlinear

optimization algorithms.

13.2 Typical sequences and the typical set

In this section, I introduce the two concepts of typical sequences and the typical set.

This concept is central to the demonstration of Shannon’s second theorem, known as the

channel coding theorem, which is described in the next section.

Typical sequences can be deﬁned according to the following. Assume an originator

message source X

generating binary sequences of length k.

Any of the 2

possible

sequences generated by X

is of the form x = x

,...,x

, where x

= 0 or 1 are the

message bits. We assume that the bit events x

are independent. The entropy of such a

source is H (X

) = kH(X ).

Assume next that the probability of any bit in the sequence

A summary is provided in T. M. Cover and J. A. Thomas, Elements of Information Theory (New York: John

Wiley & Sons, 1991), p. 191.

The notation X

refers to the extended source corresponding to k repeated observations or uses of the source

Such a property comes from the deﬁnition of joint entropy, assuming two sources with independent events:

H(X, Y ) =−



p(x, y)log

[

p(x, y)

]

=−



p(x) p(y)log

[

p(x) p(y)

]

=−



p(x)



p(y)

[

log p(x) + log p(y)

]

=−



p(x)log p(x)



p(y) −



p(x)



p(y)log p(y)

=−



p(x)log p(x) −



p(y)log p(y)

≡ H(X ) + H (Y ).

With the extended source X

, we obtain H (X

) = 2H (X ), and consequently H (X

) = kH(X ).

13.2 Typical sequences and the typical set 253

being one is p(x

= 1) = q. We, thus, expect that any sequence roughly contains kq bits

equal to one, and k(1 −q) bits equal to zero.

This property becomes more accurately

veriﬁed as the sequence length k is sufﬁciently large, as we shall see later. The probability

of a sequence θ containing exactly kq 1 bits and k(1 −q) 0 bits is

p(θ) = mq

(1 − q)

k(1−q)

, (13.21)

where m = C

is the number of possible θ sequences. Taking the minus logarithm (base

2) of both sides in Eq. (13.21) yields

−log p(θ) =−log m−log q

−log(1 −q)

k(1−q)

= log

− kq log q − k(1 −q)log(1− q)

= log

− k

[

−q log q − (1 −q)log(1− q)

]

≡ log

+ kf(q) ≡ log

+ kH(X)

≡ log

+ H (X

(13.22)

The result obtained in Eq. (13.22) shows that the probability of obtaining a sequence θ

p(θ) = m2

−kH(X)

= m2

−H (X

)

. (13.23)

Thus, all θ sequences are equiprobable, and each individual sequence in this set of size

m has the probability p(x) ≡ p(θ)/m = 2

−kH(X)

= 2

−H (X

)

. We shall now (tentatively)

call any θ a typical sequence, and the set of such sequences θ,thetypical set.

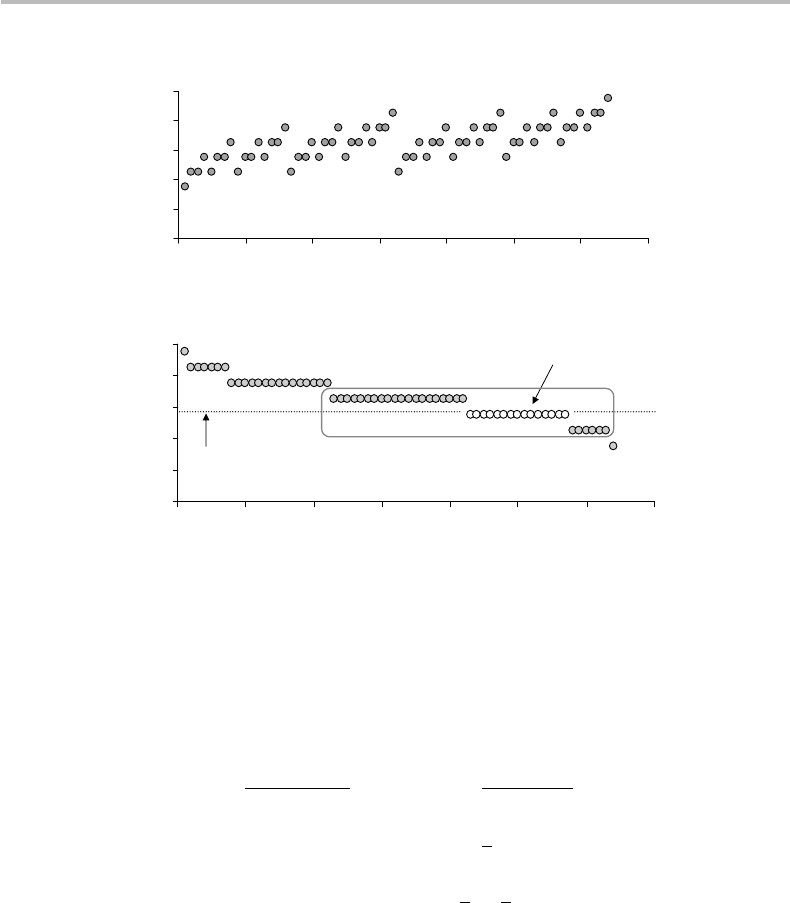
An example of a typical set (as tentatively deﬁned) is provided in Fig. 13.4.

In this example, the parameters are chosen to be k = 6 and q = 1/3. For each

sequence θ containing j bits equal to one ( j = 0, 1,...,6), the corresponding proba-

bility was calculated according to p(x) = q

(1 − q)

k−j

. The source entropy is calcu-

lated to be H(X

) = kH(X ) = kf(q) = 6 f (1/3) = 6 ×0.918 = 5.509 bit. The typical

set, thus, comprises m = C

= C

= 15 typical sequences with equal probabilities

p(x) = p(θ)/m = 2

−H (X

)

= 2

−5.509

= 0.022. The ﬁgure shows the log probabilities of

the entire set of 2

= 64 possible sequences, along with the relative size of the typi-

cal set and associated probabilities. As seen in the ﬁgure, there exist two neighboring

sets, A and B, with probabilities close to the typical set, namely −log p(x

) = 6.509

and −logp(x

) = 4.509, respectively. The two sets correspond to sequences similar to

the θ sequences with one 1 bit either in excess (A) or in default (B). Their log prob-

abilities, therefore, differ by ±1 with respect to that of the θ sequence. In particular,

For simplicity, we shall assume that kq is an integer number.

254 Channel capacity and coding theorem

10 20 30 40 50 60 70

Sequence

−log

(

)−log

(

)

(a)

(b)

Typical set

) = 5.509(

Figure 13.4 Illustration of a tentative deﬁnition of the typical set for a binary sequence with

length k = 6 and probability of 1 symbol q = 1/3 (source entropy kH(X) = 5.509 bit: (a)

probabilities (−log

p(x)) of each sequence x as ordered from x = 000000 to x = 111111; (b)

same as (a) with sequences ordered in increasing order of probability. The typical set corresponds

to sequences having kq = 2 bits equal to 1, with uniform probability −log

p(x) = kH(X ) =

5.509. The two neighboring sets, A and B, with similar probabilities are indicated.

we have

−

log p(x

Aor B

)

− H (X)

−

kH(X ) ±1

− H (X)

= 0.16.

(13.24)

Because the absolute differences deﬁned by Eq. (13.24) are small, we can now extend

our deﬁnition of the typical set to include the sequences from the sets A and B, which

are roughly similar to θ sequences within one extra or missing 1 bit. We can state that:

The sequences from A and B have roughly kq 1 bits and k(1 −q) 0 bits;

The corresponding probabilities are roughly equal to 2

−H (X

)

According to this extended deﬁnition of the typical set, the total number of typical

sequences is now N = 15 +6 +20 = 41. We notice that N ≈ 2

H(X

)

= 45.5, which

leads to a third statement:

The number of typical sequences is roughly given by 2

H(X

)

13.3 Shannon’s channel coding theorem 255

The typical set can be extended even further by including sequences differing from the

θ sequences by a small number u of extra or missing 1 bits. Their log probabilities,

therefore, differ by ±u with respect to H (X

), and the absolute difference in Eq. (13.24)

is equal to u/ k. For long sequences (k  u > 1), the result can be made arbitrarily

small.

The above analysis leads us to a most general deﬁnition of a typical sequence: given

a message source X with entropy H (X ) = f (q) and an arbitrary small number ε, any

sequence x of length k, which satisﬁes

log

p(x)

− H (X)

<ε, (13.25)

is said to be “typical,” within the error ε. Such typical sequences are roughly equiproba-

ble with probability 2

−kH(X)

and their number is roughly 2

kH(X)

. The property of typical

sequences, as deﬁned in Eq. (13.25), is satisﬁed with arbitrary precision as the sequence

length k becomes large.

Alternatively, we can rewrite Eq. (13.25)intheform



log

p(x)

− H (X)



<ε

↔

−k[H (X)+ε]

< p(x) < 2

−k[H (X)−ε]

(13.26)

which shows the convergence between the upper and lower bounds of the probability

p(x)ask increases.

Note that the typical set does not include the high-probability sequences (such as,

in our example, the sequences with high numbers of 0 bits). However, any sequence x

selected at random is likely to belong to the typical set, since the typical set (roughly)

has 2

kH(X)

members out of (exactly) 2

sequence possibilities. The probability p that x

belongs to the typical set is, thus, (roughly):

p = 2

k[H (X)−1]

= 2

−k[1−H (X)]

, (13.27)

which increases as H (X ) becomes closer to unity (q → 0.5).

13.3 Shannon’s channel coding theorem

In this section, I describe probably the most famous theorem in information theory, which

is referred to as the channel coding theorem (CCT), or Shannon’s second theorem.

The

This property is also known as the asymptotic equipartition principle (AEP). This principle states that

given a source X of entropy H (X ), any outcome x of the extended source X

is most likely to fall into the

typical set roughly deﬁned by a uniform probability p(x) = 2

−kH(X)

In the limiting case H (X ) = 1, q = 0.5, p = 1, all possible sequences belong to the typical set; they are

all strictly equiprobable, but generally they do not have the same number kq = k/2 of 1 and 0 bits. Such a

case corresponds to the roughest possible condition of typicality.

To recall, the ﬁrst theorem from Shannon, the source-coding theorem, was described in Chapter 8, see

Eq. (8.15).

256 Channel capacity and coding theorem

CCT can be stated in a number of different and equivalent ways. A possible deﬁnition,

which reﬂects the original one from Shannon,

is:

Given a noisy communication channel with capacity C, and a symbol source X with entropy

H(X ), which is used at an information rate R ≤ C, there exists a code for which message symbols

can be transmitted through the channel with an arbitrary small error ε.

The demonstration of the CCT rests upon the subtle notion of “typical sets,” as

analyzed in the previous section. It proceeds according to the following steps:

Assume the input source messages x to have a length (number of symbols) n.

With independent symbol outcomes, the corresponding extended-source entropy is

H(X

) = nH(X). The typical set of X

roughly contains 2

nH(X)

possible sequences,

which represent the most probable input messages.

Call y the output message sequences received after transmission through the noisy

channel. The set of y sequences corresponds to a random source Y

of entropy

H(Y

) = nH(Y ).

The channel capacity C is the maximum of the mutual information H (X; Y ) =

H(X ) − H(X |Y ). Assume that the source X corresponds (or nearly corresponds)

to this optimal condition.

Refer now to Fig. 13.5 and observe that:

The typical set of Y

roughly contains 2

nH(Y )

possible sequences, which represent the

most probable output sequences y, other outputs having a comparatively small total

probability.

Given an output sequence y

, there exist 2

nH(X|Y )

most likely and equiprobable input

sequences x (also called “reasonable causes”), other inputs having comparatively

small total probability.

Given an input sequence x

, there exist 2

nH(Y |X)

most likely and equiprobable output

sequences y (also called “reasonable effects”), other outputs having comparatively

small total probability.

Assume next that the originator is using the channel at an information (or code) rate

R < C per unit time, i.e., R payload bits are generated per second, but the rate is strictly

less than C bits per second. Thus nR payload bits are generated in the duration of each

message sequence of length n bits. To encode the payload information into message

sequences, the originator chooses to use only the sequences belonging to the typical set

of X. Therefore, 2

coded message sequences (or codewords) are randomly chosen

from the set of 2

nH(X)

typical sequences, and with a uniform probability. Accordingly,

the probability that a given typical sequence x

will be selected for transmitting the

coded message is:

p(x

) =

nH(X)

= 2

n[R−H (X)]

. (13.28)

C. E. Shannon, A mathematical theory of communication. Bell Syst. Tech. J., 27 (1948), 379–423, 623–56,

http://cm.bell-labs.com/cm/ms/what/shannonday/shannon1948.pdf.