Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.

16.1 Quantum bits 307
therefore,
|q=
α
|
α
|
2
+
|
β
|
2
|0+
β
|
α
|
2
+
|
β
|
2
|1, (16.5)
where α
,β
are any complex numbers.
To provide an illustration, let us come back to the analogy of the closed box containing
a coin, and tell the story again with the qubit formalism. The box has been shaken to the
point that it is impossible to tell on which side, heads or tails, the coin may be found.
We can assume without loss of generality that the coin is “fair,” and that it must rest on
either side at the bottom of the box, so that the probabilities of the coin being on heads
or on tails are strictly equal. This defines two equiprobable “coin states;” call them here
|H and
|
T
. As long as we don’t open the box, the coin remains in the superposition of
states corresponding to the qubit:
|q=
1
√
2
|H +
1
√
2
|
T
(16.6)
with the amplitudes satisfying |α|
2
=|β|
2
=(1/
√
2)
2
≡ 1/2. Thus, from the quantum
viewpoint, the coin inside the closed box does exist in both heads and tails states. The
action of opening the box and checking the physical position of the coin yields the qubit
projection |H or
|
T
, which corresponds to either of the classical bits 0 = heads or 1
= tails, respectively, with equal probabilities. This measurement is seen to collapse the
coin state |q into one of its elementary states |H or
|
T
, which yields the observable
value referred to as heads or tails. The counterintuitive, or nonclassical, conclusion
is that as long as no measurement (or state collapse) is effected, the coin dwells in
the superposition of states defined by Eq. (16.6). Note that this superposition is often
referred to as
|
+
, or “cat state,” as I shall explain.
It is possible to think of many other examples of superpositions of states. For instance,
consider a toddler in her room on an early Sunday morning. Is she still sleeping (state
|S) or is she awake and playing (state |A)? By 8 a.m. the parents know that there
is a fair chance that she must be asleep, say 90%. By 9 a.m., they know that the
odds are 50%. But if the parents don’t get up and check, the quantum view is that
by 8 a.m., the child must be in the state |S/
√
0.9 +|A/
√
0.1 and by 9 a.m. in the
state (|S+|A)/
√
2, which we have called the state |+. Only by opening the child’s
bedroom door can the actual measurement be made, which results in the state collapse
into |S or |A, giving the classical information 0 =sleeping or 1 = awake. As uncanny
as this example may sound, it illustrates the quantum concept of “superposition of
states,” now with the notion of a time evolution from the initial pure state |S to the
final pure state |A. One may view our example as a gentler, yet conceptually equivalent,
version of the Schr
¨
odinger’s cat thought experiment.
3
The stories of the tossed coin,
3
In a thought experiment, Schr
¨
odinger imagines a cat that is placed inside a sealed box. The box contains a
can of poison gas, a radioactive substance, and a Geiger counter. The decay rate of the radioactive substance
is such that after one hour, there is a 50% chance that one atom decays, which is recorded by the Geiger
counter. In this event, the counter activates the opening of the poison-gas can, resulting in the cat’s instant
death. At any time, the (poor) cat’s state can be viewed as a superposition of the pure states |deador |alive,

308 Quantum bits and quantum gates
of the sleeping toddler, and of Schr
¨
odinger’s cat illustrate the same paradox: does the
state of a macroscopic object or system require an outside observer to be defined, or is
it self-defined independent of outside observation? Our intuition tells us that such an
object or system cannot exist in two states at the same time, and, therefore, it must be its
own “observer.” The quantum-mechanics viewpoint breaks with intuition and affirms
the contrary: that objects or systems can, indeed, exist in multiple states, and that only
the observer intervention defines what the actual state turns out to be. About elementary
information, our classical mind training requires that a bit is absolutely defined as either
being 0 or 1 (regardless of possible measurement mistakes). With the qubit, we must
now retrain our mind to accept the fact that a quantum of information (the qubit) is in
a0/1 superposition state, whose outcome in observed reality remains undefined until
some measurement is performed. The next two chapters will clarify and further develop
such a most intriguing notion!
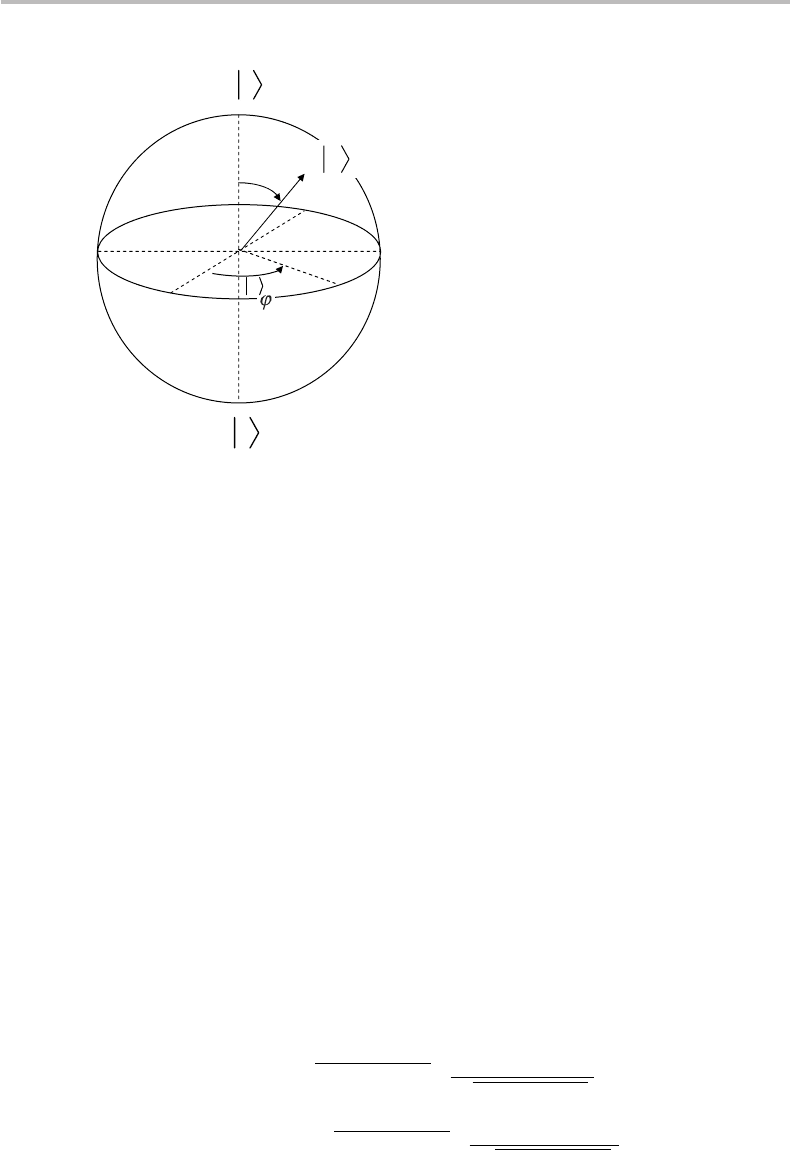
To summarize the above description so far, a qubit must be conceived as a two-
dimensional bit, whose coordinates in that space represent probability amplitudes. Since
two coordinates define the qubit, it is possible to represent it as a unique point on the sur-
face of a sphere of unity radius, called a Bloch sphere, which is described in Appendix M.
In this appendix, it is shown that the most general definition of the qubit, within an unob-
servable phase factor, is
|q=cos
θ
2
|0+sin
θ
2
e
iϕ
|1. (16.7)
The two angles θ,ϕ, thus, uniquely define the position of a point on the surface of a
sphere, just like latitude and longitude on the Earth, and as illustrated in Fig. 16.1.It
is seen from the figure that the pure qubits |0 or |1 correspond to the cases θ = 0or
θ = π , respectively, which occupy the north and south poles of the Bloch sphere. The
key conclusion is that the qubit information corresponds to an infinite number of states,
which are continuously distributed onto the surface of the Bloch sphere.
The above description concerned single qubits, corresponding to single classical bits.
It is possible to define higher-order qubits, which correspond to two classical bits or
to even longer binary codewords. Since there exist four possible pairs of classical bits,
which begins from a certain |alive and evolves over time towards a certain |dead. After the 1-hour delay,
the probabilities of the two states are equal, and the cat dwells in the state superposition
|+ =
|dead+|alive
√
2
,
hence, the name “cat state.” At any time, one cannot be sure if the cat is dead or alive, and this infor-
mation requires one to make a measurement by opening the box. Such a measurement results into the
collapse of the cat’s state into either of the pure states |dead or |alive. The initial purpose of Schr
¨
odinger’s
though experiment was to illustrate that such a quantum view must be incomplete: the cat cannot be both
dead and alive at the same time! And there is no need for someone to open the box to define in which
state the cat actually exists. Yet such a view is consistent with the so-called “Copenhagen interpreta-
tion,” according to which systems can exist in such a superposition of states until reaching state collapse
through physical observation. A fine argument, which reconciles this interpretation with Schr
¨
odinger’s
cat paradox, is the fact that a cat is a macroscopic or classical system, and, therefore, the microscopic
quantum interpretation may not apply. See discussion, and more puzzling arguments in (for instance):
http://en.wikipedia.org/wiki/Schr%C3%B6dinger’s_cat.
16.1 Quantum bits 309
a
0
q
1
q
Figure 16.1 Representation of qubit |q by a point on the surface of the Bloch sphere, as defined
by the “colatitude” angle θ and the “longitude” angle ϕ. The north and south poles correspond to
the pure qubit states |0 and |1, respectively.
namely 00, 01, 10, and 11, we can call the corresponding elementary two-qubit (or
2-qubit) states |00, |01, |10, and |11, and, similarly to Eq. (16.3), we obtain the most
general definition for any 2-qubit state:
|q=α
00
|00+α
01
|01+α
10
|10+α
11
|11. (16.8)
In this definition, the complex amplitudes α
ij
must satisfy the property
ij
+
+
α
ij
+
+
2
= 1. (16.9)
From the previous description concerning 1-qubits, it is clear that each of the terms
|α
ij
|
2
in the above summation represents the probability of finding the 2-qubit in the
state |ij, or, equivalently, of measuring the classical bit pair ij. We shall note here that
the notation |ij for a pair of qubits |i, |j , or 2-qubit |i|j actually anticipates the
concept of tensor state, which is explained in the last section of this chapter.
We can even simplify the picture of a 2-qubit by looking at it as a “four-sided die,” such
as a tetrahedron, hidden in the box. Such a die has four classically measurable outcomes
(00, 01, 10, and 11), but in the quantum world there exist an infinity of superpositions
of 2-qubit pairs, as I shall now establish.
Indeed, the 2-qubit state defined in Eq. (16.8) can also be rewritten in the form
|q=
|α
00
|
2
+|α
01
|
2
3
α
00
|00+α
01
|01
|α
00
|
2
+|α
01
|
2
4
+
|α
10
|
2
+|α
11
|
2
3
α
10
|10+α
110
|11
|α
10
|
2
+|α
11
|
2
4
(16.10)
≡ β
0
|q
0
+β
1
|q
1
,

310 Quantum bits and quantum gates
with β
0
=
|α
00
|
2
+|α
01
|
2
and β
1
=
|α
10
|
2
+|α
11
|
2
, and
|q
0
=
1
|α
00
|
2
+|α
01
|
2
(
α
00
|00+α
01
|01
)
≡ γ
00
|00+γ
01
|01
|q
1
=
1
|α
10
|
2
+|α
11
|
2
(
α
00
|10+α
01
|11
)
≡ γ
10
|10+γ
01
|11.
(16.11)
The development in Eq. (16.11) illustrates that any 2-qubit state can be conceived as the
superposition of two 2-qubits, which we call here
|
q
0
(a 2-qubit with the first bit 0),
and
|
q
1
(a 2-qubit with the first bit being 1), respectively. According to all expectation,
should we have fully assimilated the earlier story of the 1-qubit measurement, if we
attempt to measure only the first bit of any 2-qubit state, the latter must collapse into
|
q
0
or
|
q
1
, according to the outcome of the measurement being the 0 or 1 classical bits,
with associated probabilities
|
β
0
|
2
and
|
β
1
|
2
, respectively. The resulting states
|
q
0
or
|
q
1
, which represent superposition of 2-qubit states (with either 0 or 1 as the first bit),
are referred to as post-measurement states.
The above has shown that any 2-qubit state can actually be decomposed into a variety
of possible superposition of 2-qubit pairs, as selected from the family {|00, |01, |10,
|11}. Of particular interest is the specific subgroup of 2-qubit pair superpositions
|ij±|kl, where i = k or j = l, conventionally defined according to:
|β
00
≡
1
√
2
[
|00+|11
]
|β
01
≡
1
√
2
[
|01+|10
]
|β
10
≡
1
√
2
[
|00−|11
]
|β
11
≡
1
√
2
[
|01−|10
]
.
(16.12)
The family of 2-qubit superpositions defined in the above inventory is referred to as Bell
states or EPR pairs, the EPR acronym being short for the names Einstein, Podolsky, and
Rosen. The Bell or EPR states exhibit quite intriguing and useful properties for quantum
computing, as will be described in Chapter 18.
The key lesson we have learnt so far is that, unlike classical bits, qubits are not
physically observable. But, as I shall describe next, qubits can be physically manipu-
lated! Such a manipulation, which transforms the qubit state, is of consequence in the
measurable or experimental domain. Hence, we may conceive of a quantum computer,
a machine that processes information not from bits but from qubits. The fact that qubits
are a probabilistic superposition of states introduces new dimensions and perspectives
in computing power, which represents a key justification for QIT.
16.2 Basic computations with 1-qubit quantum gates
In Chapter 15, we have described the principles of reversible-logic gates, as based on
classical bit inputs and controls. Here, we shall explore how such gates can perform

16.2 Basic computations with 1-qubit quantum gates 311
elementary computations by exclusive use of qubits, instead of classical bits. As we
will discover, quantum computation based on these two principles is quite different in
nature and in power, when compared with classical computation obtained from mere
Boolean-logic gates. We shall first consider operations with single qubit states, and then
move to more complex ones involving two and three qubit states.
As we have seen earlier in this chapter, a single qubit (or 1-qubit), |q, is defined
through its complex amplitudes (α, β) with respect to a given orthonormal base or pure
states (|0, |1), also referred to as computational basis. A quantum gate, call it A, has
the effect of transforming an input qubit state |q into an output qubit state |q
,using
predefined control qubits. Thus, the relation between the input and output states can be
expressed in the equivalent matrix-vector relation:
|q
=A|q. (16.13)
In quantum vocabulary, the entity A that transforms |q into |q
is referred to as an
operator. Since the vector |q
must remain on the Bloch sphere surface (so that its
squared amplitudes correspond to actual probabilities), it must be a unitary vector. For
this reason, the transformation from |q to |q
is called unitary, and A must be a unitary
operator. We shall now further develop the notion of unitary transformation and the
relation between unitary operator and matrix.
For simplicity and to escape any further conceptual burden, so far we have assumed
that qubits are equivalent to vectors in a 2D space. This view is simplistic, but accurate.
Consistently, we may assume that the transformation operator A may be defined through
a2× 2 matrix, whose coefficients are defined by four complex numbers, a
ij
.Fromthe
definitions Eq. (16.3) and Eq. (16.13), we, thus, obtain the matrix-vector equation in the
|0, |1 base:
|q
=A|q
=
a
11
a
12
a
21
a
22
α
β
=
a
11
α + a
12
β
a
21
α + a
22
β
≡
(
a
11
α + a
12
β
)
|0+
(
a
21
α + a
22
β
)
|1
≡ α
|0+β
|1.
(16.14)
Such a relation between the input (α, β) and output (α
,β
) amplitudes does not account
for the control qubits in the quantum gate, but for the time being this will suffice for our
description.
The result in Eq. (16.14) shows that the action of the quantum gate, or that of
the quantum operator A, modifies the state amplitudes of the initial superposition,
according to the transformations α → α
= a
11
α + α
12
β and β → α
21
α + α
22
β. Since
the output state amplitudes (α
,β
) must correspond to probabilities, it is required that

312 Quantum bits and quantum gates
|α
|
2
+|β
|
2
= 1. As I have mentioned earlier, such a transformation and the associated
operator/matrix, must be unitary.
4
In the following, we shall consider five examples of 2 ×2 unitary operators or matrices
and their effect on qubit transformation, namely: the Pauli matrices (called I, X, Y, and
Z-gates) and the Hadamard matrix (also called a H-gate).
Pauli matrices or I, X, Y, Z-gates
The Pauli matrices (named after the physicist W. Pauli) or I, X, Y, Z-gates are defined
as:
I ≡ σ
0
=
10
01
X ≡ σ
x
= σ
1
=
01
10
Y ≡ σ
y
= σ
2
=
0 −i
i 0
Z ≡ σ
z
= σ
3
=
10
0 −1
.
(16.15)
The different notations I = σ
0
, X = σ
x
= σ
1
, Y = σ
y
= σ
2
and Z = σ
z
= σ
3
are usually
found in the related literature for historical reasons. It is easily established that the squares
of all the above matrices are equal to unity or X
2
= Y
2
= Z
2
= (σ
i
)
2
= I
2
= I .
The first matrix I is the identity matrix, which corresponds to the classical REPEAT
gate and leaves the input qubit |q=α|0+β|1 invariant, according to
|q
=I |q
=
10
01
α
β
=
α
β
≡ α|0+β|1≡|q.
(16.16)
The second matrix X (or X-Pauli) corresponds to the classical NOT gate. Indeed, we
obtain
|q
=X |q
=
01
10
α
β
(16.17)
=
β
α
≡ β|0+α|1,
4
A transformation and associated matrix A is unitary if the following identity is satisfied A
−1
= ( A
T
)
∗
≡ A
+
.
In this definition, A
−1
is the inverse matrix of A (such that A
−1
A = AA
−1
= I ), A
T
is the transposed matrix
of A (with coefficients a
ij
→ a
ji
), and
∗
denotes complex conjugation (a
ij
→ a
∗
ij
). The symbol
+
stands
for Hermitian conjugation, which combines both transposition and complex conjugation (a
ij
→ a
∗
ji
), i.e.,
A
+
is the Hermitian conjugate of the matrix A.

16.2 Basic computations with 1-qubit quantum gates 313
showing that the elementary qubits |0, |1 are switched into their counterparts |1, |0,
which for a state superposition |q=α|0+β|1 amounts to swapping the amplitude
probabilitie according to (α, β) → (β, α). Thus, if the input |q is in the pure state, for
instance |q=|0 (or α = 1,β = 0), the output state is |q
=|1, and the reverse with
|q=|1, which gives |q
=|0. In these two limiting cases, this operation, indeed,
corresponds to that of a classical NOT gate. But generally, it is also correct to call
X,σ
1
,σ
x
a quantum NOT gate.
The action of the Y-gate is both to swap the amplitudes and to introduce a π phase
shift between the two states of the initial superposition,
5
according to
|q
=Y |q
=
0 −i
i 0
α
β
=
−i β
i α
=−i (β|0−α|1) ≡ e
iγ
(β|0+e
iπ
α|1),
(16.18)
where γ =−π/2 is an immeasurable, or “unobservable” phase constant.
Finally, the action of the Z -gate is only to introduce a π phase shift between the two
states of the initial superposition, according to
|q
=Z|q
=
10
0 −1
α
β
=
α
−β
≡ α|0−β|1≡α|0+e
iπ
β|1.
(16.19)
As can also be easily checked, the three Pauli matrices X, Y, Z exhibit the following
properties:
σ
1
σ
2
= i σ
3
σ
2
σ
3
= i σ
1
σ
3
σ
1
= i σ
2
σ
i
σ
j
=−σ
j
σ
i
(i = j).
(16.20)
One defines the commutator of two operators or matrices A, B as [A, B] = AB − BA.
Two operators or matrices are said to commute if [ A, B] = 0. Then we observe from
the last equation in Eq. (16.20) that for i = j the Pauli matrices do not commute, i.e.,
σ
i
,σ
j
=σ
i
σ
j
− σ
j
σ
i
= 2σ
i
σ
j
, and, in the general case
σ
i
,σ
j
=2δ
ij
σ
i
σ
j
, (16.21)
where δ
ij
is the Kronecker symbol.
6
We,thus,have[σ
1
,σ
2
] = 2σ
1
σ
2
= 2iσ
3
,[σ
2
,σ
3
] =
2σ
2
σ
3
= 2iσ
1
and [σ
3
,σ
1
] = 2σ
3
σ
1
= 2iσ
2
. The commutator between any two Pauli
5
With complex numbers, a change of sign corresponds to a phase shift of ±π , or a multiplying factor of
e
±iπ
=−1, since e
±iπ
= cos(±π ) + isin(±π ) =−1.
6
Namely: δ
ij
= 1fori = j,andδ
ij
= 0fori = j.

314 Quantum bits and quantum gates
matrices can be generalized in the formula
[σ
i
,σ
j
] = 2iε
ijk
σ
k
, (16.22)
where ε
ijk
is the Levi–Civita symbol.
7
Likewise, using the property (σ
i
)
2
= I , we can
generalize Eq. (16.20) in the formula:
σ
i
σ
j
= iε
ijk
σ
k
+ δ
ij
I. (16.23)
These properties of the Pauli matrices or I, X, Y, Z-gates are used extensively in quantum
computing, as will be illustrated. In Appendix N, I show that the Pauli matrices constitute
a universal base, making it possible to generate any unitary 2 ×2 matrices or unitary
operators U , which represent the universal building blocks for 2-qubit quantum gates
and circuits.
Hadamard matrix gate or H-gate
The Hadamard matrix gate,orH-gate, is defined as:
H =
1
√
2
11
1 −1
≡
1
√
2
(X + Z ). (16.24)
Using results in Eqs. (16.17) and (16.19), we can interpret the action of the Hadamard
gate as follows:
|q
=H |q
=
1
√
2
(X + Z )|q
=
1
√
2
(X |q+Z |q)
=
1
√
2
[(β|0+α|1) +(α|0−β|1)]
= α
|0+|1
√
2
+ β
|0−|1
√
2
≡ α|+ + β|−.
(16.25)
It is seen from the above that the Hadamard gate transforms any input qubit |q=
α|0+β|1 into the superposition |q=α|+ + β|−, where |+, |− represent a new
pure states basis. As we shall see later, the two pure-state bases |0, |1 and |+, |−
play a fundamental role in quantum computing.
The action of the above 2 ×2 quantum gates on input qubits is summarized in
Table 16.1.
7
With the following definition (see http://en.wikipedia.org/wiki/Levi-Civita_symbol)
ε
ijk
=
+1if(i, j, k)is(1, 2, 3), (2, 3, 1) or (3, 1, 2),
−1if(i, j, k)is(3, 2, 1), (1, 3, 2) or (2, 1, 3),
0 otherwise: i = j or j = k or k = i.

16.3 Quantum gates with multiple inputs and outputs 315
Table 16.1 Action of the elementary 2 × 2 quantum gates on input qubit |q=α|0+β|1.
Gate U Output |q
=U|q Action
Identity, I,σ
0
α|0+β|1 Invariant
X,σ
1
,σ
x
β|0+α|1 Swaps amplitudes
Y,σ
2
,σ
y
β|0+e
iπ
α|1 Swaps amplitudes and π shift between amplitudes
Z,σ
3
,σ
z
α|0+e
iπ
β|1 π shift between amplitudes
Hadamard, H α|+ + β|− Switches to |+, |− basis
For illustration purposes, consider two examples showing the action of cascades of
2 × 2 quantum gates:
U = XZX →
U |q=XZX(α|0+β|1)
= XZ(β|0+α|1)
= X (β|0+e
iπ
α|1)
= e
iπ
α|0+β|1
= e
iπ
(α|0+e
−iπ
β|1)
≡ α|0−β|1,
(16.26)
U = HX →
U |q=HX(α|0+β|1)
= H (β|0+α|1)
≡ β|+ + α|−.
(16.27)
Finally, we must note that the 2 ×2 Pauli and Hadamard matrix gates correspond
to reversible 1-qubit computations. Indeed, any input qubit can be retrieved through
the double operations X
2
= Y
2
= Z
2
= H
2
= I
2
= I . More generally, any gate cor-
responding to a unitary matrix or operator U is reversible by the application of the
Hermitian conjugate U
+
, since, by definition, U
+
U = I . This property also applies to
gate cascades UVW ...of unitary operators, which have for their Hermitian conjugate
(UVW ...)
+
=···W
+
V
+
U
+
, thus,
(UVW ...)
+
UVW =···W
+
V
+
U
+
UVW =···W
+
V
+
VW =···W
+
W =···I.
16.3 Quantum gates with multiple qubit inputs and outputs
With the background from the previous section on 2 × 2 quantum gates and that
from reversible logic gates introduced in Chapter 15, we can now describe the matrix
representation and operation of various higher-order quantum gates, which have two
or more 1-qubit inputs and outputs. The elementary gates of this type are called
CNOT, CROSSOVER, controlled-U, controlled-SWAP, Toffoli, and CCNOT, which
I shall review in the following.
316 Quantum bits and quantum gates
CNOT
0
10
ab
a
b
+=
x
10
ab
+=
x
x
0
1
x
1
10´ +=
x
b
a
10´ +=
x
|a> |x> |a
´
>|x
´
>
0101
00
00
1
110
1
011
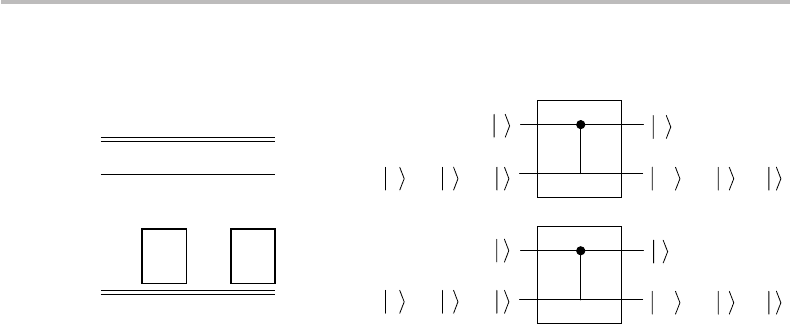
Figure 16.2 CNOT gate with control qubit
|
a
and target qubit |x, with truth table and gate
output |a, |x
resulting from target qubit superposition |x=α|0+β|1.
CNOT gate
Consider first the CNOT gate, whose diagram is shown in Fig. 16.2. The gate has a
control qubit |a=|0 or |a=|1, and a target qubit |x=α|0+β|1. Here, we
shall assume that the control qubits are in pure states, namely, |0, |1.Thefigure
shows the action of the CNOT gate with the corresponding truth table. It is seen
from the figure that the target qubit |x is left unchanged when the control qubit is
|a=|0 while in the case |a=|1 the amplitudes α, β of |x are swapped which,
as we have seen in the previous section, represents the quantum NOT version of a
qubit.
But how can we define the CNOT gate matrix, since here we have a control qubit?
To answer this, recall that in the case of 1-qubit gates, the matrix is defined in the
computational base |0, |1. In the case of the CNOT gate, the matrix must be defined in
the extended computational base, noted {|a|x} = {|0|0, |0|1, |1|0, |1|1}, which
covers all possible gate inputs according to the truth table shown in Fig. 16.2, with |a=
|0 or |a=|1 and |x=|0 or |x=|1 (the matrix applying to any superposition
thereof). As will be described further on in this chapter, the state |a|x is referred to as
the tensor product of the kets |a and |x. In the computational base {|0|1}, the input
tensor state |a|x is represented by a four-dimensional column-vector with coordinates
u
1
, u
2
, u
3
, u
4
,
|
a
|x=
u
1
u
2
u
3
u
4
, (16.28)
which satisfies |u
1
|
2
+|u
2
|
2
+|u
3
|
2
+|u
4
|
2
= 1. The output state of the gate is then
given by the matrix-vector relation |a
|x
=A|a|x, where A is the gate’s 4 ×
4 matrix. In the case of the CNOT gate, and as expressed in the tensor base
