Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


16.3 Quantum gates with multiple inputs and outputs 317
Table 16.2 Transformation of input qubit |a|x of coordinates (u
1
, u
2
, u
3
, u
4
) in computational basis
{|0|0, |0|1, |1|0, |1|1} into output qubit |a
|x
=A
CNOT
|a|x.
u
1
u
2
u
3
u
4
|a|x|a
|x
Observations
10 0 0 |0|0|0|0 Invariant
01 0 0 |0|1|0|1 Invariant
00 1 0 |1|0|0|1 xqubit flipped
00 0 1 |1|1|1|0 xqubit flipped
11 0 0
1
√
2
(|0|0+|0|1) =|0|+
1
√
2
(|0|0+|0|1) =|0|+ Invariant
00 1 1
1
√
2
(|1|0+|1|1) =|1|+
1
√
2
(|1|0+|1|1) =|1|+ Invariant
αβ 00
α|0|0+β|0|1
=|0(α|0+β|1)
α|0|0+β|0|1
=|0(α|0+β|1)
Invariant
00 αβ
α|1|0+β|1|1
=|1(α|0+β|1)
β|1|0+α|1|1
=|1(β|0+α|1)
x qubit amplitudes
swapped
{|a|x} = {|0|0, |0|1, |1|0, |1|1}, the matrix takes the form:
A
CNOT
=
I 0
0 X
≡
1000
0100
0001
0010
. (16.29)
The 2 × 2 reduced form of the above gate matrix shows that states of the form |0|x
are invariant (sub-matrix I ), while states of the form |1|x have the target qubit |x
flipped (sub-matrix X ). Although somewhat tedious, it is useful to verify now the above
result by applying the gate matrix A
CNOT
to the input state |a|x.FromEqs.(16.28) and
(16.29), we obtain:
|a
|x
=A
CNOT
|a|x=
u
1
u
2
u
4
u
3
=
1000
0100
0001
0010
u
1
u
2
u
3
u
4
= u
1
|0|0+u
2
|0|1+u
4
|1|0+u
3
|1|1.
(16.30)
The right-hand side of Eq. (16.30) can now be developed according to different input
possibilities for |a|x, i.e., concerning the control qubit |a and the target qubit |x.
Table 16.2 shows the result with the target qubit |x as being in either a pure state
(first four lines) or a superposition of states (last four lines). As expected, the table
illustrates that the CNOT gate leaves the target qubit |x=|0 or |1 invariant when the
control qubit is set to |a=|0. If the target qubit is a superposition |x=α|0+β|1,
the amplitudes (α, β) are either conserved (|a=|0) or swapped (|a=|1). In the
specific case α = β = 1, the target qubit remains invariant regardless of the control
qubit |a, as expected. It is left as an exercise to analyze the action of the CNOT gate
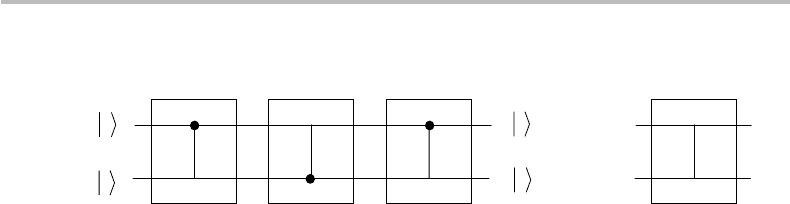
318 Quantum bits and quantum gates
a
b
x
b
a
x
x
A
CNOT
A
CNOT
B
CNOT
x
x
(a) (b)
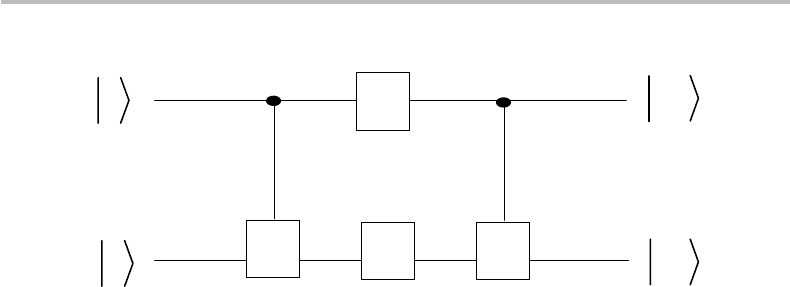
Figure 16.3 (a) Quantum gate circuit based on the concatenation of three CNOT gates, with
corresponding matrices A
CNOT
(control qubit at top) and B
CNOT
(control qubit at bottom).
(b) Equivalent circuit representation (CROSSOVER or SWAP).
with the control qubit |a being now in a superposition of states, and show that for
certain combinations of input qubits |a|x, the CNOT gate can generate any of the four
EPR or Bell states, as defined in Eq. (16.2).
It is easily verified that the matrix A
CNOT
is unitary and that its inverse matrix is
A
−1
CNOT
= A
CNOT
,orA
2
CNOT
= I (I = 4 ×4 identity matrix). This last result is expected,
since the repeated action of CNOT (with same control qubit, by inherent circuit con-
struction) must leave the target qubit invariant.
CROSSOVER or SWAP gate
It is also possible to build circuits made of concatenated CNOT gates, where the control
and target qubits exchange roles, i.e., an output target qubit from a first gate serving
as an input control qubit for the next gate. Consider, for instance, the three-gate circuit
shown in Fig. 16.3, which (as we shall see) corresponds to the CROSSOVER or SWAP
operator. The circuit is seen to include in the middle a CNOT gate arranged upside
down, thus, using the target output qubit of the first CNOT gate as a control for the
second CNOT gate. For simplicity, we assume that the control qubits that are input to
CNOT gates must be in a pure state. Under this assumption, this whole circuit must be
input only with pure states |a, |b=|0, |1. The matrix representation of the CNOT
gate makes it possible to construct the circuit shown in Fig. 16.3, with care to properly
define the matrix B
CNOT
corresponding to the reversed arrangement. As an exercise, one
may show that in the computational base
{
|0|0, |0|1, |1|0, |1|1
}
the matrix B
CNOT
takes the form
B
CNOT
=
1000
0001
0010
0100
. (16.31)
A second exercise is to compute the circuit matrix A
SWAP
= A
CNOT
B
CNOT
A
NOT
from
the matrix definitions in Eqs. (16.29) and (16.30). The computation yields
A
SWAP
=
1000
0010
0100
0001
. (16.32)
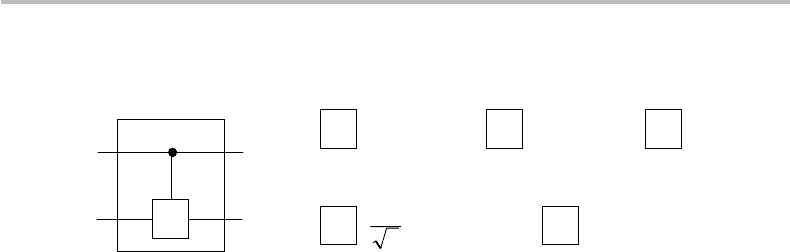
16.3 Quantum gates with multiple inputs and outputs 319
U
X
01
10
Y
−
0
0
i
i
Z
−10
01
S
i0
01
H
−11
11
2
1
(a) (b)
Figure 16.4 (a) Controlled-U gate, (b) corresponding matrix gate possibilities U = X, Y, Z , H,
and S.
It is seen from the coefficients in the matrix A
SWAP
that the input tensor states |0|0 and
|1|1 are left invariant (owing to the 1 coefficients in the matrix-diagonal), while the
input tensor states |0|1and |1|0are swapped (owing to the 1 off-diagonal coefficients).
The circuit gate thus corresponds to a CROSSOVER or SWAP function, as Fig. 16.3
indicates with the outputs |b, |a. The equivalent gate representation is also shown at
right in the figure.
Controlled-
U
gates
In the category of controlled-U gates, U stands for any quantum gate with a 2 × 2
unitary (but not necessarily Hermitian) matrix. For instance, U = X, Y, Z , H (Pauli and
Hadamard gates) and S (π/2 phase gate), as illustrated in Fig. 16.4 with their 2 × 2
matrices represented in the |0, |1 state basis. The gate controlled-X is the same as
CNOT and its matrix (previously called A
CNOT
)isshowninEq.(16.29). We notice again
from this equation that this 4 × 4 matrix can also be represented in the reduced form
controlled-X = A
CNOT
=
I 0
0 X
, (16.33)
where the top-left side corresponds to the REPEAT or invariant function (control qubit set
to |0, corresponding to 2 ×2 identity matrix I ) and the bottom-right side corresponds to
the NOT function (control qubit set to |1, corresponding to 2 ×2matrixX). Thus, we can
most generally define the matrix of any controlled-U gate (e.g., U = X, Y, Z , H, S ...)
according to
controlled-U =
I 0
0 U
. (16.34)
Most generally, any controlled-U gate corresponds to a target qubit rotation characterized
by U = R
n
(θ), where R
n
(θ)istherotation operator associated with the transformation
U on the Bloch sphere, as characterized by a rotation angle θ about the axis parallel to
the unitary vector n (see Appendix N for related definition and properties).
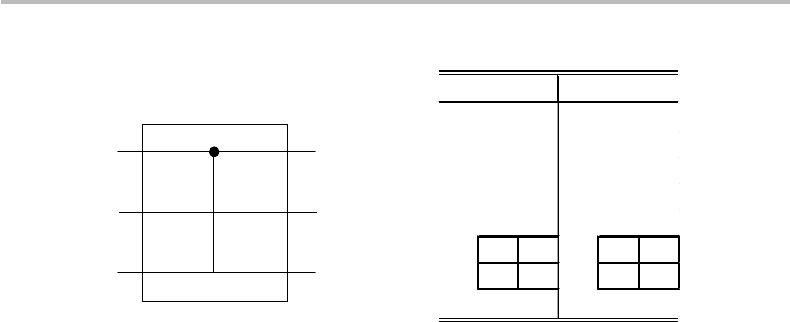
320 Quantum bits and quantum gates
Controlled-SWAP
c
a
b
x
c
´
a
x
´
b
|c > |a > |b > |c
´
>|a
´
>
|
b
´
>
000000
001001
010010
011011
100100
1
01
1
10
1
10
1
01
111111
Figure 16.5 Controlled-SWAP gate with truth table.
Controlled-SWAP gate
The schematic representation of a controlled-SWAP gate and its qubit truth table are
shown in Fig. 16.5. This gate represents a particular case of the Fredkin gate previously
described in Chapter 15, and represented in Fig. 15.7 (with the control qubit c at the
bottom). Since this is a 3 ×3 gate, the state basis has eight tensor elements {|c|a|b}=
{|0|0|0, |0|0|1,...,|1|1|1}, with the first state |c corresponding to the control
qubit. In this basis, and using the definition of A
SWAP
in Eq. (16.32),the8×8matrix
A
C-SWAP
takes the reduced and explicit forms:
A
C-SWA P
=
I 0
0 A
SWAP
≡
10000000
01000000
00100000
00010000
00001000
00000010
00000100
00000001
. (16.35)
Toffoli or CCNOT gate
In Chapter 15, we have seen that the Toffoli gate corresponds to the logical function
controlled-controlled-NOT, or CCNOT. To recall, in the classical version of the Toffoli
gate, a, b are two control bits, and c is the “target” bit to process. The gate then outputs
a, b, c
with c
= c ⊕ab, meaning that, classically, the Toffoli gate is an XOR gate
with ab and c as inputs, together with the conservation of the control bits a, b, to ensure
computational reversibility. Here, consider that the input–output information is not about
“bits” but “qubits.” Defining the two control qubits as |c
1
, |c
2
, and the target bit as
|a, it is easily established that in the basis {|c
1
|c
2
|a} the corresponding 8 × 8matrix
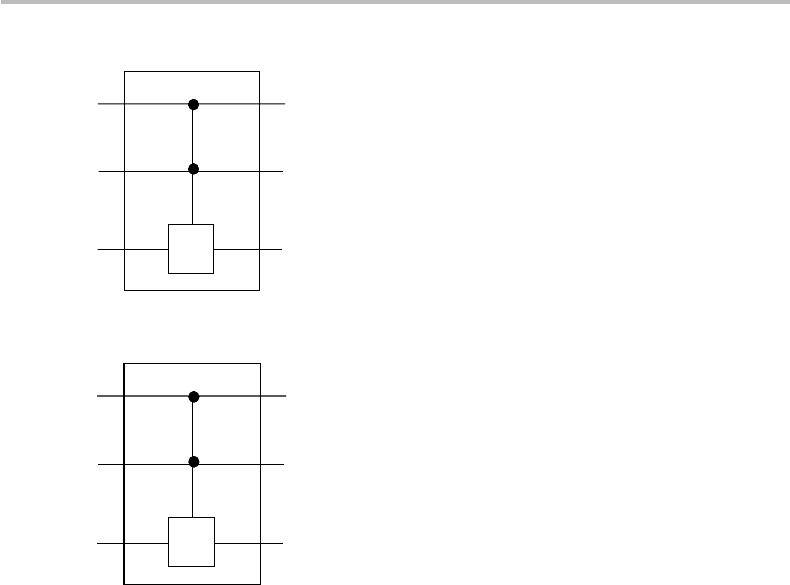
16.3 Quantum gates with multiple inputs and outputs 321
X
=
X
I
CCNOT
0
0
Figure 16.6 Controlled-controlled-X or CCNOT or Toffoli gate.
U
=
U
I
CC
U
0
0
Figure 16.7 Controlled-controlled-U,orCCU, gate with corresponding 8 × 8matrixinreduced
form.
takes the form
A
Toffoli
=
I 0
0 X
≡
10000000
01000000
00100000
00010000
00001000
00000100
00000001
00000010
, (16.36)
where I is the 6 × 6 identity matrix and X is the 2 × 2 quantum NOT matrix. The
quantum circuit representation of the CCNOT gate and its reduced matrix are provided
in Fig. 16.6. It is clear that the CCNOT gate transforms the target qubit |a into X |a,if
and only if |c
1
=|c
2
=|1 and leaves |a invariant when |c
1
=|c
2
=|0.
Controlled-controlled-
U
or CC
U
gate
This is a 3-qubit gate similar to the CCNOT or Toffoli gate, except that one uses any
unitary transform U for the 2 × 2 operator, see Fig. 16.7, along with the corresponding
reduced matrix. It is clear that the CCU gate transforms the target qubit |a into U |a,
if and only if |c
1
=|c
2
=|1 and leaves |a invariant when |c
1
=|c
2
=|0.

322 Quantum bits and quantum gates
R
=
R
I
CC
R
0
0
Figure 16.8 Deutsch gate or CCR gate, with corresponding 8 ×8 matrix in reduced form, where
R is a unitary rotation operator.
Deutsch or CC
R
gate
A particular type of CCU gate, called the Deutsch gate, is obtained when one chooses
U ≡ R
n
(θ), as shown in Fig. 16.8. To make the Deutsch gate, a restriction applies to
the rotation angle θ . Indeed, in the Deutsch gate the angle θ should be incommensurate
with π , which means that θ/π is not a rational fraction.
8
With such a property, any qubit
|v on the Bloch sphere that lies at an angle ±xθ from the gate’s target qubit |u can
be reached with arbitrary precision by applying the CCR gate a finite number of times
k, i.e., |w=R
k
(±θ)|u=R(±kθ)|u can be made arbitrarily close to |v if k/x ≈ 1.
In particular, the rotation angle kθ can be made arbitrarily close to π/2, which makes
the Deutsch gate closely similar to a Toffoli gate (R(π/2) = X ). Consider, finally, that
single 2 × 2 rotations defined as R ≡ R
n
(θ) make it possible to transform any input
qubit |uinto any output qubit |von the Bloch sphere. A controlled-R gate has the same
complete transformation capability on the 2-qubit space, and a CCR or Deutsch gate
on the 3-qubit space. It is beyond the scope of this chapter to establish formally that,
actually, quantum circuits based only on 3-qubit CCR or Deutsch gates and CCNOT
gates are capable of achieving any n-qubit transformations in the n-qubit space.
16.4 Quantum circuits
The matrix representation of 2- and 3-qubit gates may look somewhat impractical to
handle, except in generic cases when they can be put in some reduced form. Therefore,
it would seem that quantum-gate circuits with multiple gates and control qubits are not
easy to model and analyze. In reality, however, gate circuits are far simpler to handle! I
shall illustrate this through a few examples. Consider first the 2-qubit quantum circuit
involving single-qubit gates (J, K ) and controlled-U gates as shown in Fig. 16.9, with,
for instance, J = X . The circuit is seen to involve two different controlled-U gates
(U, U
) and two single-qubit gates (X, K ), where U, U
, K are any unitary gates. We
do not need to calculate the corresponding matrix. Instead, consider the evolution of the
8
A rational fraction or rational number can be expressed as the ratio a/b of two integers a, b.
16.4 Quantum circuits 323
X
U
a
a
x
´
´
x
K
´
U
Figure 16.9 Basic example of 2-qubit quantum circuit.
input tensor state |a|xthrough the circuit, assuming separately |a=|0and |a=|1,
with each of the arrows (→) representing the crossing of a gate:
|0|x→|0|x→X |0K |x=|1U
K |x
|1|x→|1U|x→X|1KU|x=|0KU|x.
(16.37)
If, for instance, we let U = Y , K = S and U
= Z (according to the standard definitions
of Y, Z, S in Fig. 16.4), we obtain:
|0|x→|1ZS|x=|1ZS(α|0+β|1)
=|1Z(α|0+iβ|1)
=|1(α|0−iβ|1)
= α|1|0−iβ|1|1
|1|x→|0SY|x=|0SY(α|0+β|1)
=|0S(β|0−α|1)
=|0(β|0−iα|1)
= β|0|0−iα|0|1.
(16.38)
Letting β = 0orα = 1inEq.(16.38), we obtain the transformation:
u
1
|0|0+u
2
|0|1+u
3
|1|0+u
4
|1|1
→ u
1
|1|0−iu
2
|1|1−iu
3
|0|1+u
4
|0|0
= u
4
|0|0−iu
3
|0|1+u
1
|1|0−iu
2
|1|1,
(16.39)
which corresponds to the circuit matrix and its reduced form:
A =
0001
00−i0
1000
0 −i00
≡
0 −iSX
S
+
0
. (16.40)
As a second illustrative example, consider next the 2-qubit quantum circuit shown in
Fig. 16.10, which involves two CNOT gates, three gates A, B, C, and a δ-phase gate S.
9
It is further assumed that ABC = I . As before, the evolution of the input tensor state
9
A δ-phase gate has for matrix S =
10
0e
iδ
.
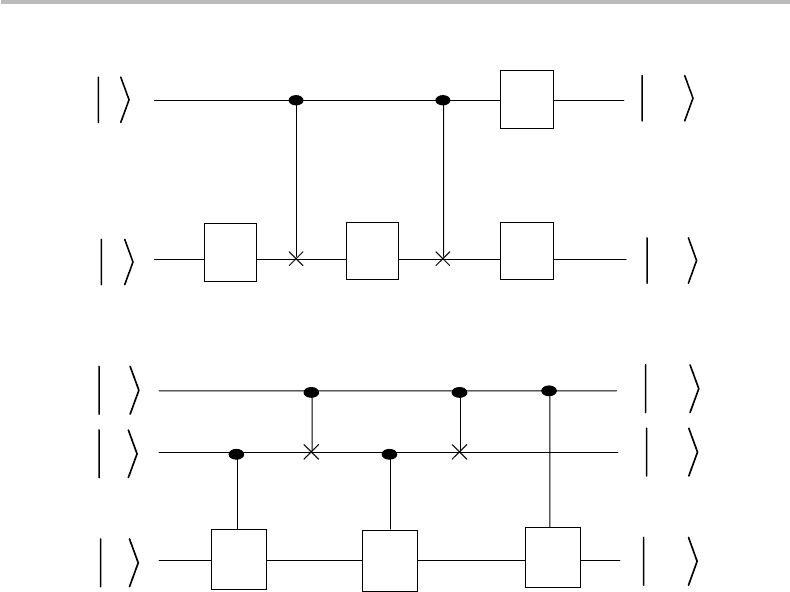
324 Quantum bits and quantum gates
C
a
´
a
x
´
x
B A
S
Figure 16.10 Two-qubit quantum circuit with ABC = I and δ-phase gate S.
V
b
´
b
x
´
x
+
V
V
a
´
a
Figure 16.11 Three-qubit quantum circuit with V
2
= U .
|a|x through the circuit is calculated through the following:
|0|x→|0C|x→|0C|x→|0BC|x→|0BC|x→S|0ABC|x=|0|x
|1|x→|1C|x→|1XC|x→|1BXC|x
→|1XBXC|x→e
iδ
|1AXBXC|x.
(16.41)
Letting U = e
iδ
AXBXC, the above transformation reduces to
|0|x→|0|x
|1|x→e
iδ
|1e
−iδ
U |x=|1U|x.
(16.42)
The result shows that when
|
a
=|0 the circuit leaves the target qubit |x invariant, and
when
|
a
=|1 the target qubit is transformed into U |x. This is the definition of the
controlled-U gate. Actually, the equivalence of the circuit shown in Fig. 16.10 and the
controlled-U gate stems from Euler’s theorem, which is demonstrated in Appendix N.
The theorem states that for any 2 ×2 unitary transformation U , there exist three matrices
A, B, C satisfying ABC = I and for which U = e
iδ
AXBXC, where δ is an arbitrary
phase.
As a third illustrative example, consider next the 3-qubit quantum circuit shown in
Fig. 16.11, which involves two CNOT gates, and three controlled-U gates based on
a unitary operator V and its Hermitian conjugate V
+
. The property V
2
= U is also
assumed. Let us walk the input state |a|b|x through the quantum circuit, considering
the four possibilities for the control qubits |a|b=|0|0, |0|1, |1|0, |1|1.This
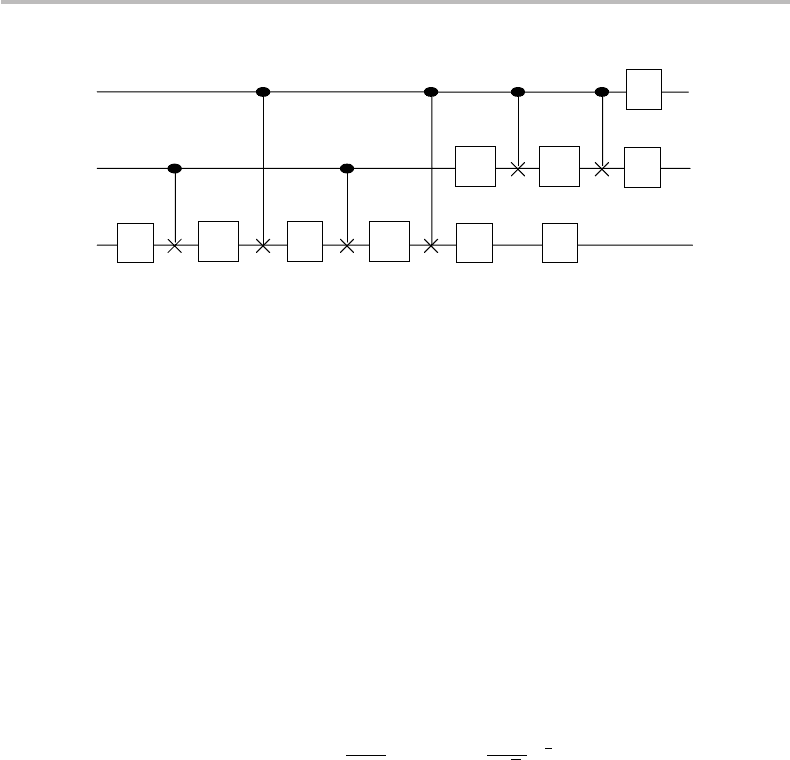
16.4 Quantum circuits 325
H
T
+
T
+
T
T H
+
T
+
T
S
T
Figure 16.12 Three-qubit quantum circuit with Hadamard gates (H), ±π/4-phase gates (T, T
+
),
and a single π/2-phase gate (S), which is equivalent to a CCNOT or Toffoli gate.
gives:
|0|0|x→|0|0|x→|0|0|x→|0|0|x→|0|0|x→|0|0|x
|0|1|x→|0|1V |x→|0|1V |x→|0|1V
+
V |x
=|0|1|x→|0|1|x→|0|1|x
|1|0|x→|1|0|x→|1|1|x→|1|1V
+
|x→|1|0V
+
|x→|1|0VV
+
|x
=|1|0|x
|1|1|x→|1|1V |x→|1|0V |x→|1|0V |x→|1|1V |x→|1|1VV|x
≡|1|1U |x. (16.43)
We observe from the above result that when |a|b =|1|1 the circuit leaves the target
qubit |x invariant, and when |a|b=|1|1 the target qubit is transformed into U |x.
This is the definition of a controlled-controlled-U ,orCCU gate, whose representation
and matrix are shown in Fig. 16.7. It is straightforward to verify that in the case
V =
1 − i
2
(I + iX) =
1 − i
√
2
e
i
π
4
X
, (16.44)
we have U = V
2
= X , and the CCU gate reduces to the previously described CCNOT
or Toffoli gate (Fig. 16.6).
10
As another example, consider the elaborate quantum circuit shown in Fig. 16.12,
which includes Hadamard gates (H ), ±π/4-phase gates (T, T
+
), and a single π/2-
phase gate (S). It is left as an exercise to establish that this quantum circuit is actually a
possible equivalent realization of a Toffoli or CCNOT gate.
As a final example of complex quantum circuits, consider the plain-adder circuit
described in Chapter 15 for reversible computation with classical bits. We can now
conceive of it as a quantum circuit capable of performing plain addition with qubits. The
corresponding building blocks are the quantum gate circuits SUM and CARRY, which
are based on CNOT and CCNOT or Toffoli gates, as shown in Fig. 16.13.Giventwo
qubit operands |x, |y and a carry qubit |c, the outputs |x ⊕ y, |x ⊕ y ⊕ c represent
the quantum equivalents of XOR or modulo-2 addition. Note the qubit output |c
in
the CARRY gate circuit; this represents the carry result of the plain addition between
10
For the exponential-operator representation in the right-hand side, see Appendix N.
326 Quantum bits and quantum gates
SUM
c
x
x
y
x
cyx
CARRY
x
x
x
0
c
x
x
y
c
x
c
yx
´
c
Figure 16.13 Quantum gate circuits SUM and CARRY, built from CNOT and CCNOT or Toffoli
gates.
0
b
C
C
x
∗
C
S
∗
C
S
S
0
0
a
0
1
b
1
a
0
2
b
2
a
0
C
0
d
0
0
a
0
1
d
1
a
0
2
d
2
a
0
Figure 16.14 Quantum plain-adder for two qubit registers |a
0
|a
1
|a
2
, |b
0
|b
1
|b
2
,asbasedon
gate circuits SUM (S) and CARRY (C)showninFig. 16.13.ThegateC
∗
corresponds to the
reverse operation of the CARRY gate.
|x, |y and |c. Also note the ancilla bit |0 at the CARRY gate input. A 10-qubit
plain-adder circuit, which is homologous to that described in Chapter 15 for classical
computing, is shown in Fig. 16.14. This circuit performs the quantum addition of two
qubit registers containing 3-qubits each, namely |a
0
|a
1
|a
2
, |b
0
|b
1
|b
2
, and outputs
the result as |d
0
|d
1
|d
2
. As discussed in Chapter 15, this circuit architecture can be
extended to perform plain addition with registers of any size.
11
As also discussed in the
previous chapter, the circuit can be reversed (i.e., traversed from right to left) to perform
subtraction, including the generation of a “negative sign” qubit. Furthermore, the con-
catenation of the circuit makes it possible to perform operations such as multiplication
and exponentiation in modular algebra. One must not conclude, however, that quan-
11
As adapted from V. Vedral and M. B. Plenio, Basics of quantum computation. Prog. Quant. Electron., 22
(1998), 1–39.
