Денисов-Винский Н.Д. Mathcad при решении задач по Высшей математики. 3 курс

Подождите немного. Документ загружается.

Негосударственное образовательное учреждение

высшего профессионального образования

Московский институт энергобезопасности и энергосбережения

КАФЕДРА

ЕСТЕСТВЕННОНАУЧНЫХ И ОБЩЕТЕХНИЧЕСКИХ ДИСЦИПЛИН

Н.Д. ДЕНИСОВ-ВИНСКИЙ

Mathcad

III курс

Теория вероятностей и

математическая статистика

Москва 2009

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Mathcad. III курс. Теория вероятностей и математическая статистика. –

М.: МИЭЭ, 2009, 93 с.

Одобрено кафедрой естественнонаучных и общетехнических дисцип-

лин МИЭЭ: 17 сентября 2009 г.

Автор: Н.Д. Денисов-Винский

Редакторы: Семёнов С.В.

Ерохин С.В.

Автор выражает свою благодарность рецензенту к.т.н., доценту ка-

федры «Электротехники и электроники» МИЭЭ Черёмухину Василию

Ефимовичу, за полезные замечания и дополнения, которые послужили

улучшению настоящего издания.

Автор с благодарностью примет от читателей все критические заме-

чания и указания по адресу: denisov.vinskiy@yandex.ru

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

СОДЕРЖАНИЕ

Введение

1. Случайные события

1.1. Пространство элементарных событий

1.2. Основы комбинаторики. Число перестановок и число сочета-

ний

2. Случайные величины

2.1. Функция распределения

2.2. Свойства функции распределения

2.3. Дискретные случайные величины

2.4. Непрерывные случайные величины

2.5. Свойства плотности распределения

2.6. Математическое ожидание и дисперсия

3. Основные распределения случайных величин

3.1. Биномиальное распределение

3.2. Распределение Пуассона

3.3. Равномерное распределение

3.4. Экспоненциальное распределение

3.5. Нормальное распределение

4. Элементы математической статистики

4.1. Понятие выборки

4.2. Понятие генератора случайных числе

4.3. Функции создания случайных чисел с различными законами

распределения

4.4. Выборочное математическое ожидание и дисперсия

4.5. Интервальные оценки

5. Элементы прикладной статистики

5.1. Общие понятия регрессии

5.2. Линейная регрессия

5.3. Экспоненциальная регрессия

5.4. Синусоидальная регрессия

5.5. Линейная регрессия общего вида

6. Пример решения домашних задач

7. Литература

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

ВВЕДЕНИЕ

При подготовке студентов в МИЭЭ по специальности Электро-

снабжение особое место занимает преподавание естественнонауч-

ных дисциплин и математики, как универсального инструмента

для познания других дисциплин. Обучение построено таким обра-

зом, что все разделы, которые будут изучены студентом в курсе

математики, пригодятся ему при изучении дальнейших дисциплин,

в том числе специальных. Именно поэтому курс математики вклю-

чает в себя только самые важные и необходимые темы. В ходе со-

ставления курса была проведена определённая работа по включе-

нию в разделы математики тех тем, которые находят наибольшее

отражение в других дисциплинах по специальности «Электро-

снабжение».

При изучении данного пособия необходимо обратить внимание

на следующее:

1. Жирным шрифтом выделены команды, располагающиеся

либо в меню системы Mathcad, либо на панелях рабочего

окна. Например: Matrix (Матрицы) меню Insert (Встав-

ка).

2. Примеры взятые непостредствено из системы Mathcad бу-

дут располагаться по середине страницы.

3. Пример, взятый из Mathcad для визуализации теории, как

правило имеет внизу комментарий.

4. В книге приведены отрывки из учебного пособия Ерохина

С.В. «Теория вероятности и математическая статистика»

для того, чтобы студенту было удобнее работать с учебным

пособием.

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

1. СЛУЧАЙНЫЕ СОБЫТИЯ

1.1. ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ СОБЫТИЙ

Теория вероятностей — раздел математики, изучающий за-

кономерности случайных явлений, наблюдаемых при многократ-

ном повторении опыта. Результаты опытов (экспериментов) назы-

ваются событиями. События бывают составными и элементар-

ными (ω).

Пример: Пусть опыт состоит в подбрасывании игральной кос-

ти и наблюдении числа выпавших очков X. Тогда можно ввести

следующие элементарные случайные события: {X = 1}, {X = 2}, ...

, {X = 6}, и составные события, состоящие из нескольких элемен-

тарных {2 < X < 6}, {X - четно}, {X - нечетно} и т.д.

В системе Mathcad элементарные события могут быть записаны

в виде матрицы-строки или матрицы-столбца (Рис. 1.1.1).

Рис. 1.1.1. Пример записи случайного события в системе Mathcad

Совокупность Ω всех элементарных событий ω в опыте называ-

ется пространством элементарных событий.

Событие называется невозможным, если при повторении опы-

та оно никогда не происходит (выпадение 7 очков при броске иг-

ральной кости).

Возможности системы Mathcad ограничены при работе со слу-

чайными событиями. Это связано с тем, что при работе со случай-

ным событиями не требуется применения специальных функций и

операций. В подавляющем большинстве при работе со случайными

событиями и в общем в теории вероятности используется элемен-

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

тарные операции сложения, вычитания, умножения и деления. Ис-

ключения составляют только некоторые операции. Например это

функция, вычисляющая число перестановок и число сочетаний.

Данная функция распространена в теории вероятности. Рассмот-

рим её вычисление в системе Mathcad.

1.2. ОСНОВЫ КОМБИНАТОРИКИ

ЧИСЛО ПЕРЕСТАНОВОК И ЧИСЛО СОЧЕТАНИЙ

Существуют задачи теории вероятности, которые требуют зна-

ния комбинаторики. Комбинаторика изучает приёмы нахождения

числа различных комбинаций, составленных из данных предметов

(элементов дискретного множества предметов) при определённых

условиях. Напомним ее основные формулы.

Допустим, есть n различных предметов. Сколькими способами

можно расставить их по порядку? Например, три предмета 1, 2 и 3

можно расставить следующими способами: 123, 132, 213, 231, 312,

321. Итого, 6 вариантов. Если же предметов N, то число таких ва-

риантов





...321!

- число размещений.

Усложним задачу: теперь из n различных предметов нужно вы-

брать k )( nk



. Порядок выбираемых предметов не важен, важно

лишь какие предметы будут выбраны. Например, при выборе двух

предметов из трех 1, 2, 3 возможны следующие варианты: 1 и 2, 1 и

3, 2 и 3. В общем случае число вариантов вычисляется по формуле

)!(!

knk





Число

C называется числом сочетаний из n по k (читается:

С из n по k). Например:

.10

120

)!25(!2









C

Очевидно,



CC .

Для работы с задачами комбинаторики в Mathcad предусмот-

рены две следующие функции:

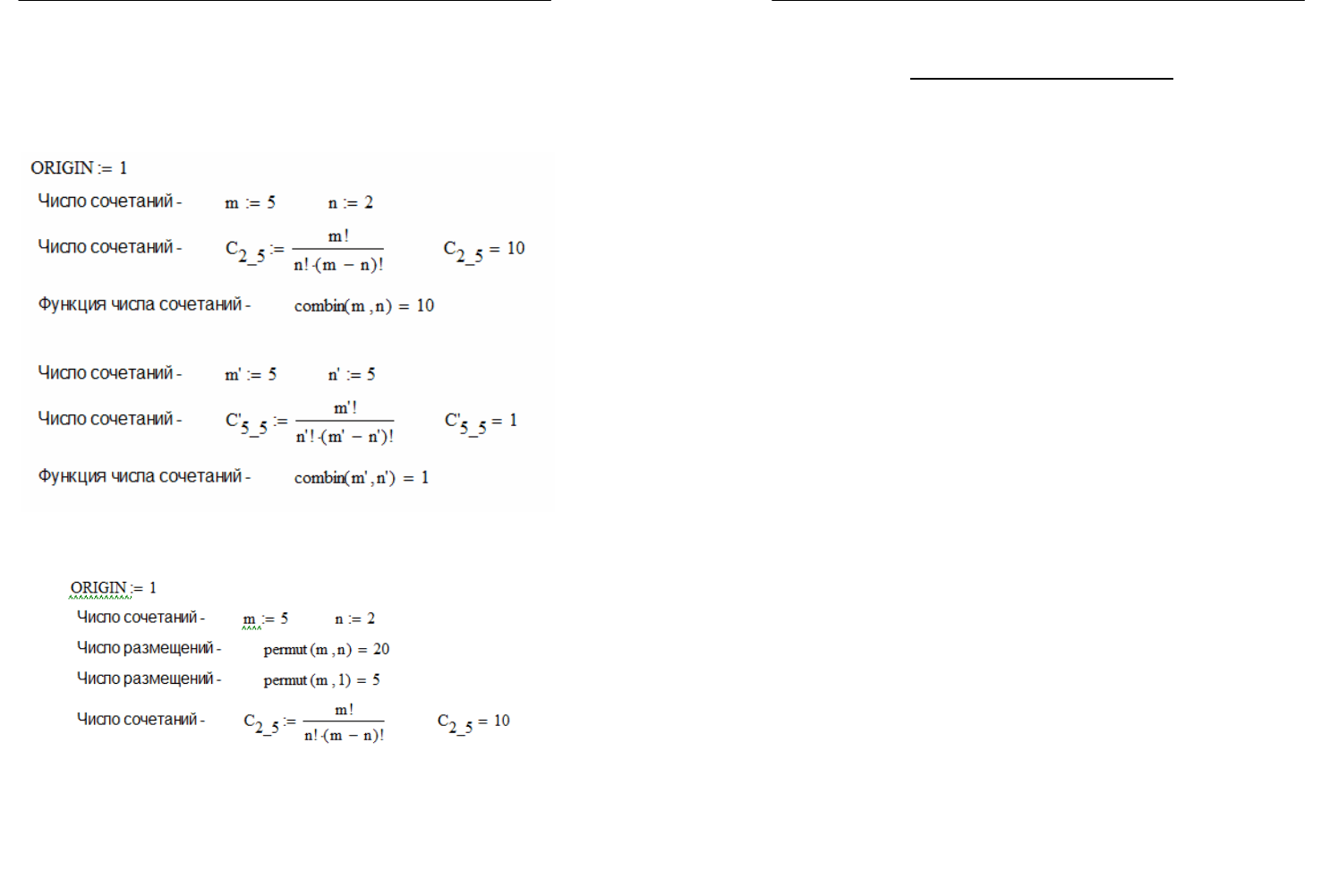
Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

- функция permut(n, m) – вычисление числа размещений;

- функция combin(m, n) – вычисление числа сочетаний.

Пример использования функции combin(m,n) (Рис. 1.2.1.) и

permut(n, m) (Рис. 1.2.2.).

Рис. 1.2.1. Пример применения функции combin(m,n)

для вычисления числа сочетаний

Рис. 1.2.2. Пример применения функции permut(m,n)

для вычисления числа размещений

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

2.1. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Случайной величиной Х называется функция элементарного

события ω с областью определения Ω и областью значений R. Дру-

гими словами, случайная величина принимает случайные числовые

значения. Эти значения называются реализациями случайной ве-

личиной Х

Многие величины науке и технике, а также повседневной жиз-

ни, являются случайными. Время, затрачиваемое на дорогу, коли-

чество заявок на телефонную станцию, прибыль организации,

рост человека, количество пораженных целей при стрельбе и т. д.,

все это описывается случайными величинами. Важнейшую роль

случайные величины играют и в энергетике. Срок службы обору-

дования, время технического обслуживания также являются слу-

чайными величинами.

Случайные величины будем обозначать прописными (большими)

латинскими буквами X, Y, Z.

Законом распределения случайной величины называется лю-

бое правило (таблица, функция), позволяющее находить вероятно-

сти всех возможных событий, связанных со случайной величи-

ной.

Для описания случайной величины рассмотрим вероятность

P{Х ≤ х} для различных х. Это вероятность того, что случайная ве-

личина окажется меньше некоторого числа х.

Функция F

(x) = P{Х ≤ х}, определенная для всех чисел x, на-

зывается функцией распределения случайной величины Х.

Далее для простоты записи мы будем обозначать

F(x) = F

(x) = Р{Х ≤ х} .

Функция распределения является одной из форм закона рас-

пределения для случайной величины всех типов и однозначно оп-

ределяет случайной величиной. Далее вместо фразы «случайная ве-

личины, имеющая функцию распределения F[x] » будем говорить

для краткости: «случайная величина с распределением F(x)» .

Случайные величины могут быть непрерывными, так и дис-

кретными.

В Mathcad функцию распределения можно задать таким же

способом, как и обычную функцию.

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

2.2. СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

Вспомним из курса математики некоторые свойства функций

распределения.

1) F(x) определена для всех х.

2) 0 ≤ F(x) ≤ 1 для всех х, как F(x) — вероятность.

3) F(x

) — F(x

) = P{x

< X ≤ x

}, если x

> x

4) F(x

) ≥ F(x

) для x

> x

, т.е. F(x) не убывает.

2.3. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайная величина называется дискретной, если множество

ее возможных значений конечно или счетно.

Простейшей формой закона распределения дискретной слу-

чайной величины с конечным множеством значений является ряд

распределения

= Р{Х = x

}, который задается аналитически или

таблицей.

Х х

… x

…

P p

… p

…

Например, опыт состоит в броске игрального кубика, а элемен-

тарным событием является количество выпавших очков. Число

возможных реализаций случайной величины конечно и равно 6.

Если предположить, что выпадение любых граней равноверо-

ятно, то ряд распределения для данной случайной величины имеет

вид:

Х 1 2 3 4 5 6

P 1/6 1/6 1/6 1/6 1/6 1/6

В Mathcad дискретные случайные величины можно при помо-

щи матриц – а точнее векторов: они же матрицы-столбцы и матри-

цы-строки (См. рис. 2.3.1. и 2.3.2.).

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Рис. 2.3.1. Пример задания дискретных случайных величин

Другой пример с бросанием игральной кости.

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Рис. 2.3.2. Пример задания дискретных случайных величин

2.4. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайная величина X с непрерывной функцией распределения

называется непрерывной.

Непрерывная случайная величина не может принимать каких-то

конкретных значений, можно говорить лишь о вероятности попа-

дания реализации случайной величины в какой-либо интервал.

Примерами непрерывных случайных величин являются: время

службы прибора и т. п.

Для непрерывной случайной величины невозможно построить

ряд распределения, поэтому их определяют по-другому.

Плотностью распределения случайной величины X называет-

ся неотрицательная кусочно-непрерывная функция f

(x), для кото-

рой при любом х

выполняется соотношение

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru







dttfxF ,)()(

где F

(x) – функция распределения случайной величины.

Для простоты дальнейших обозначений будем пи-

сать f(x) = f

(x). Плотность вероятности является одной из форм

закона распределения для непрерывных случайных величин.

2.5. СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ

1) f(x) ≥ 0 для всех х, т. е. плотность неотрицательна. Плотность

фактически есть вероятность, а вероятность не может быть отрица-

тельной.







 ,1)( dttf

т.е. выполняется условие нормировки плотно-

сти. (См. рис. 3.5.1.)





}{)(

xxxPdttf - это основное свойство плотно-

сти. Для того, чтобы вычислить вероятность попадания случайной

величины в интервал, достаточно посчитать площадь под графи-

ком плотности случайной величины над этим интервалом. Таким

образом, чем выше значения плотности в точке, тем больше веро-

ятность для случайной величины принять значение в окрестности

этой точки.

4) F'(x) = f(x). Это свойство устанавливает простую взаимо-

связь между плотностью и функцией распределения.

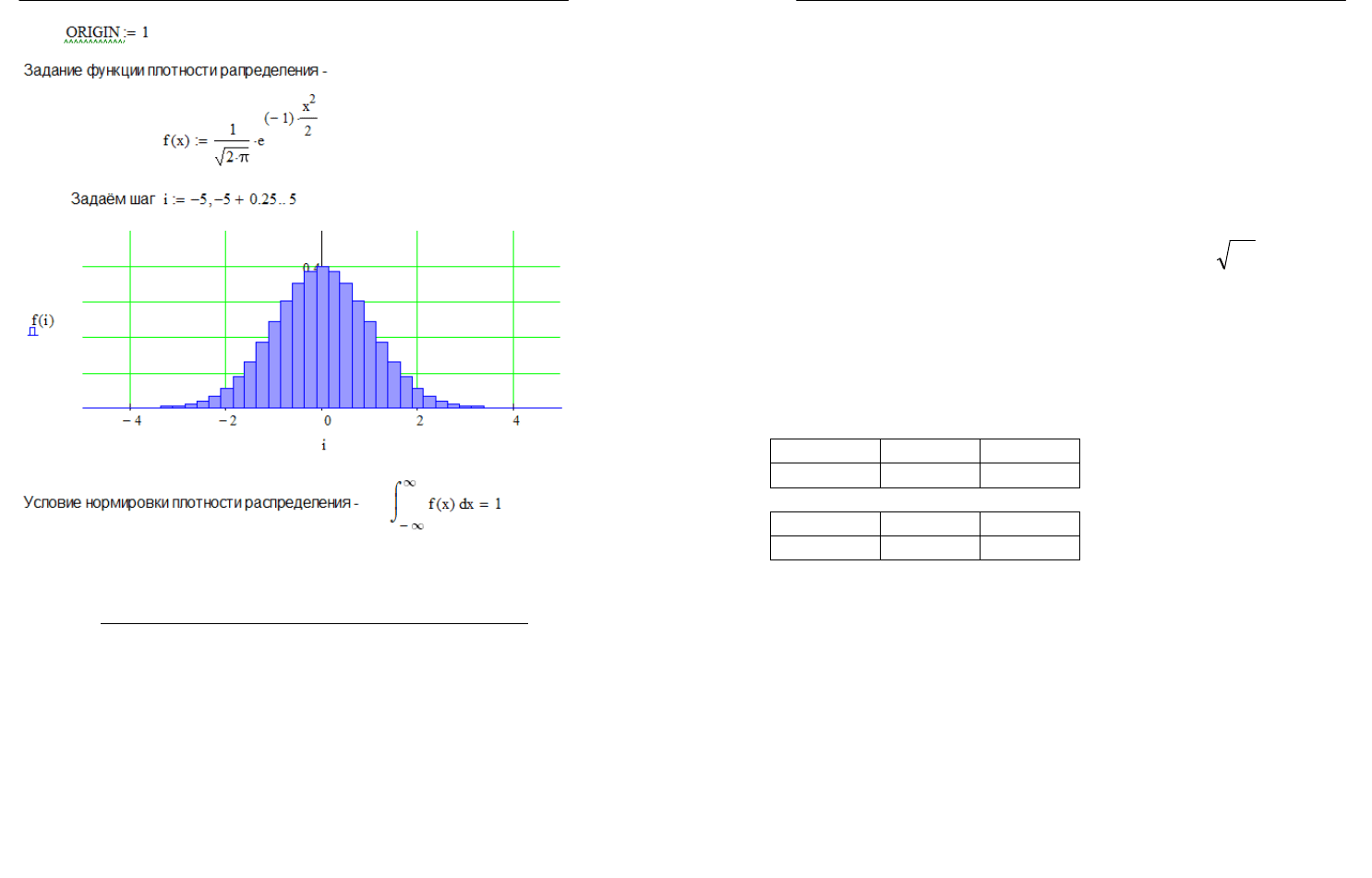
Для примера рассмотрим плотность распределения стандарт-

ного нормального распределения -

)(

exf







Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Рис. 2.5.1. Нормировка функции плотности распределения

2.6. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ

Случайные величины могут быть дискретными и непрерывны-

ми. Если Х – непрерывная случайная величина c плотностью f(x) то

ее математическое ожидание и дисперсия вычисляются по форму-

лам:







 ;)( dxxfxm







 .)()(

dxxfmxd

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Математическим ожиданием дискретной случайной вели-

чины называется число





xpXM

][ . Оно обозначается также

символом m

. Математическое ожидание является своеобразным

"средним" значением случайной величины.

Дисперсией дискретной случайной величины называется число







xkk

mxpXD

)(][ . Она обозначается d

. Чаще рассматри-

вают среднее квадратическое отклонение .

d



Дисперсия характеризует рассеивание значений случайной ве-

личины относительно ее математического ожидания.

Пример.

Вычислить математическое ожидание и дисперсию двух слу-

чайных величин:

СВ 1

-1 1

P 1/2 1/2

СВ 2

-100 100

P 1/2 1/2

Для СВ1 получаем:

;05,015,0)1(



.15,0)01(5,0)01(



Для СВ2 получаем:

;05,01005,0)100(



.100005,0)0100(5,0)0100(



Таким образом, математические ожидания величин совпадают,

а дисперсии отличаются в 10000 раз.

Далее приведён пример решения этой задачи в системе Math-

cad (Рис. 2.6.1.).

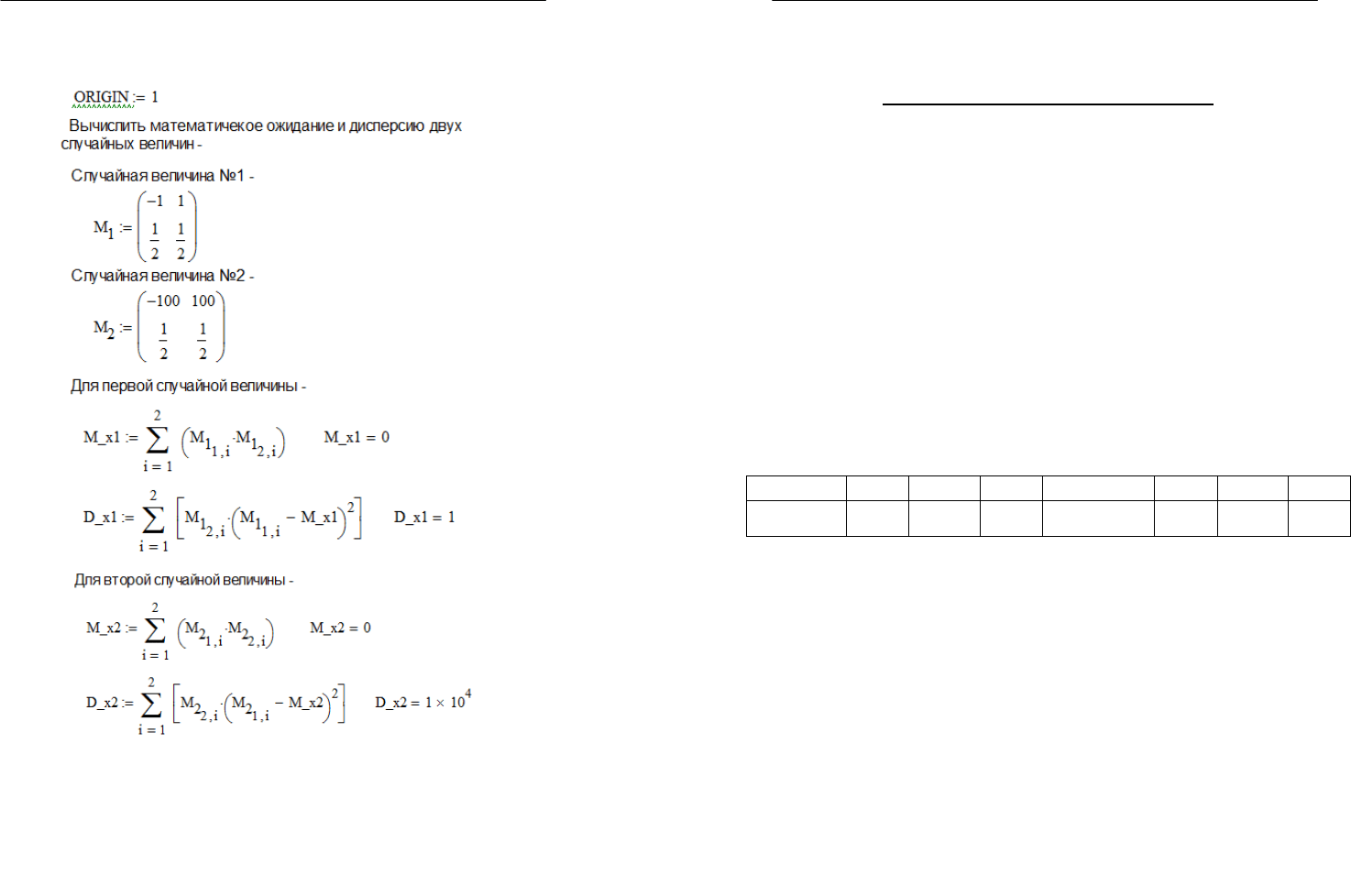
Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Рис. 2.6.1. Вычисление математического ожидания и дисперсии

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

3. ОСНОВНЫЕ РАСПРЕДЕЛЕНИЯ

СЛУЧАЙНЫХ ВЕЛИЧИН

3.1. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Пусть опыт повторяется

раз, вероятность успеха каждый раз

равна

, вероятность неудачи pq





1 (согласно схеме Бернул-

ли).

Рассмотрим случайную величину

– число успехов после

опытов. Очевидно, она принимает все целочисленные значения от

0 до

По формуле Бернулли:

.}{

knkk

qpCkXP





Данное распределение называется биномиальным распреде-

лением и обозначается Bi(n,p).

Ряд распределения представлен в таблице:

X~Bi(n,p)

0 1 … k … n-1 n

P q

npq

n-1

…

knkk

qpC



… nqp

n-1

Математическое ожидание и дисперсия биномиально распре-

делённой случайной величины вычисляются по следующим фор-

мулам:

npxM



][

npqxD



][ .

Решим пример сначала «вручную», потом используя простые

арифметические функции среды Mathcad, а после чего разберём

специальные функции среды Mathcad для работы с биномиальным

распределением.

Пример.

Стрелок стреляет по трем мишеням. Вероятность поразить каж-

дую равна р = 0,6. Построить ряд распределения случайная вели-

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

чина Х – число пораженных мишеней. Вычислить ее математиче-

ское ожидание и дисперсию.

Решение.

Эта случайная величина распределена по биномиальному зако-

ну. Она принимает значения 0, 1, 2 и 3. Вычислим вероятности по

формуле Бернулли:

;064,0}0{

 qXP

;288,0}1{

 npqXP

;432,0}2{

 qpCXP

.216,0}3{

 pXP

Составляем ряд распределения:

X 0 1 2 3

P 0,064

0,288

0,432 0,216

Математическое ожидание и дисперсию можно вычислить по

ряду распределения, но проще воспользоваться формулами:

M[X] = np = 3∙0,6 = 1,8;

D[X] = npq = 3∙0,6∙0,4 = 0,72.

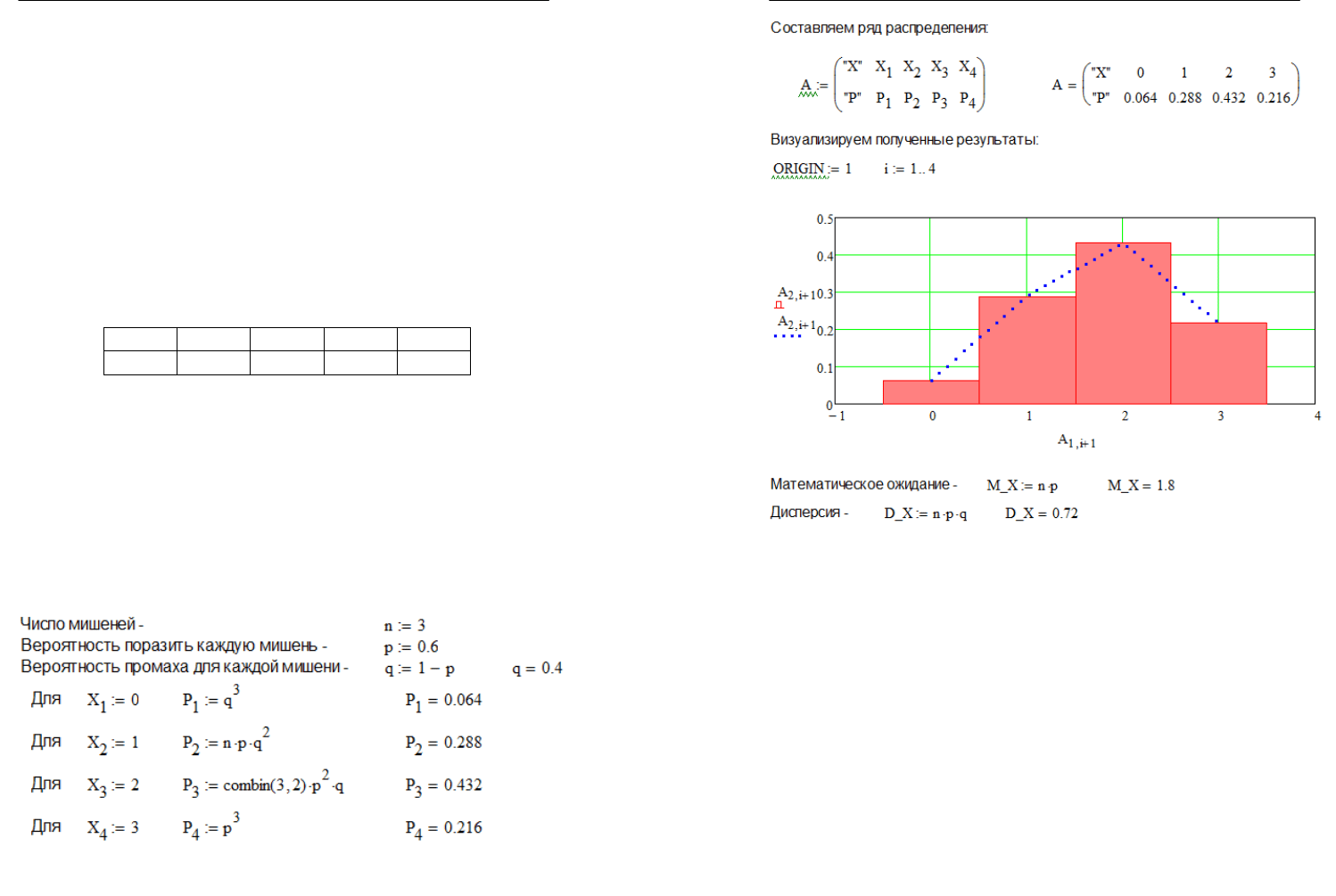
Теперь решим этот пример при помощи простых арифметиче-

ских функций среды Mathcad (Рис. 3.1.1.).

Рис. 3.1.1.(а) Построение ряда распределения случайной величины

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Рис. 3.1.1.(б) Построение ряда распределения случайной величины

Вычисление математического ожидания и дисперсии

В системе Mathcad есть ряд специальных функций, которые

описывают основные распределения случайных величин. Функция

в системе Mathcad, которая описывает ряд распределения вероят-

ности по биномиальному закону, называется dbinom(k,n,p).

Это функция, которая выдаёт массив данных в зависимости от

количества испытаний n, а также вероятности удачного исхода ка-

ждого испытания p. Переменная k является счетчиком числа успе-

хов и принимает значения от 1 до n.

Синтаксис её записи в системе Mathcad может быть записан

следующим образом:

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

nk ..1:



),,( pnkdbinomP



Результатом вычисления этой функции будет массив данных P,

который полностью сопоставлен с набором событий от 1 до n.

Помимо функции плотности распределения для биномиального

закона распределения, существует также функция распределения.

Она записывается следующим образом:

pbinom(k,n,p)

Как и функция ряда распределения, эта функция возвращает

массив данных, который полностью соответствует событию X, n –

количество испытаний, p – положительный исход каждого испы-

тания, k – это счётчик массива.

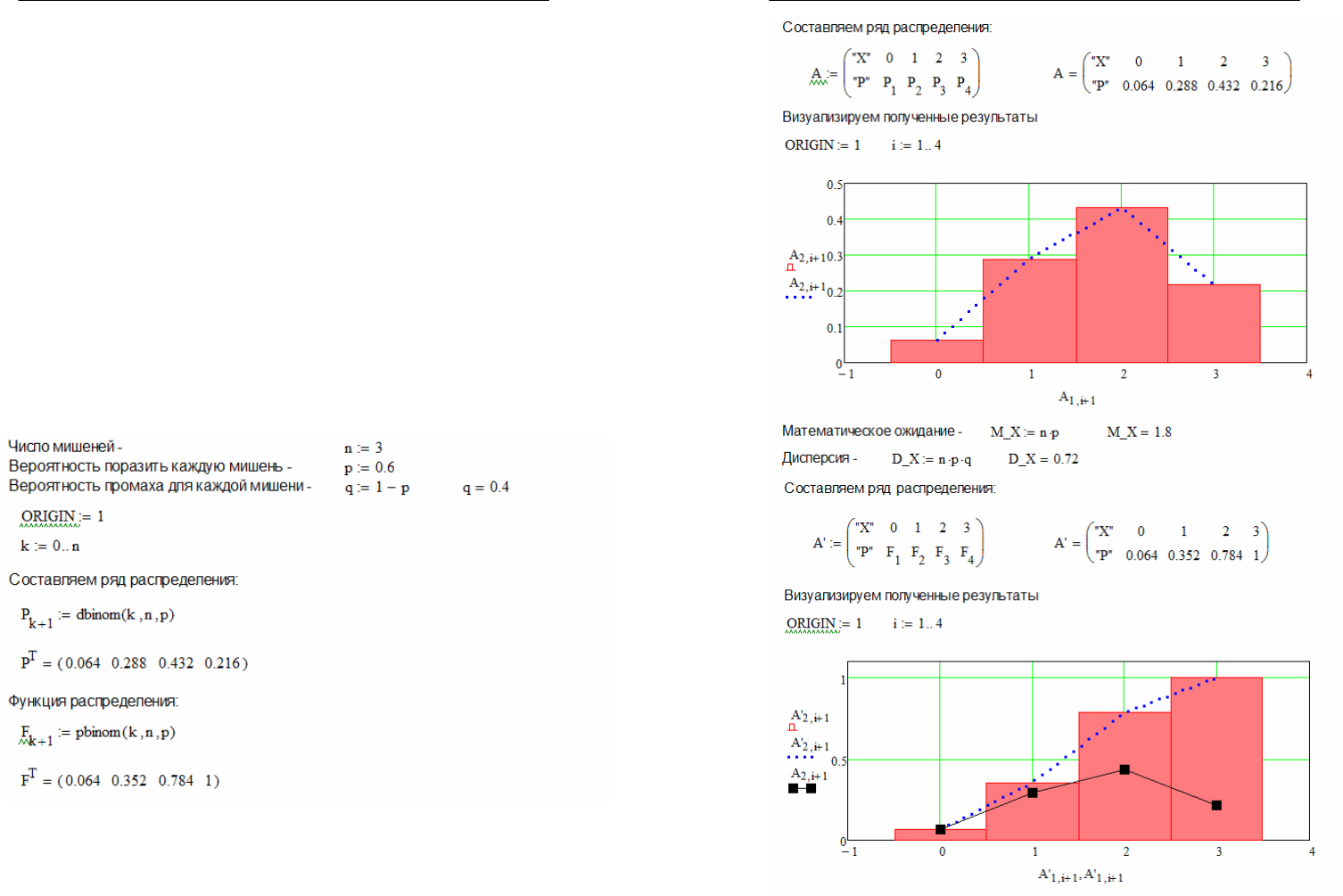
Теперь рассмотрим пример решения выше поставленной задачи

при помощи этих функций системы Mathcad (Рис. 3.1.2.).

Автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru