Денисов-Винский Н.Д. Mathcad при решении задач по Высшей математики. 3 курс
Подождите немного. Документ загружается.


Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
61
где VX – вектор значений по оси
OX
, VY – вектор значений
по оси
OY
, а Guess – вектор начальных приближенных парамет-
ров экспоненциальной регрессии.
Таким образом, для того, чтобы построить экспоненциальную
регрессию необходимо задать два вектора данных, а также задать
вектор начальных приближённых параметров экспоненциальной
регрессии.
Смотрите примеры ниже (Рис. 5.3.1 и рис. 5.3.2).
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
62
Рис. 5.3.1. Построение экспоненциальной регрессии
Рассмотрим другой пример.

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
63
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
64
Рис. 5.3.2. Построение экспоненциальной регрессии
По большому счёту характер результирующей кривой не зави-
сит от того, какие будут введены приближённые параметры экспо-
ненциальной регрессии. При этом конечно не стоит вводить в пер-
вом столбце ноль, так как в уравнении CeAxH
xB
)( первое
слагаемое обнулиться и результатом приближения будет прямая,
параллельная оси
OX
.
5.4. СИНУСОИДАЛЬНАЯ РЕГРЕССИЯ
Рассмотрим ещё одну регрессию, функция которой также име-
ет широкое распространение в технике - особенно в электронике –
это синусоидальная регрессия.
Так же как и в случае с экспоненциальной регрессией запишем
общим вид синусоидальной функции:

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
65
CBxAxH
)sin()(
Хотя этот общий вид и не является окончательным общим ви-
дом, так как под знаком синуса отсутствует переменная при
x
,
однако она достаточна для того, чтобы полностью описать сину-
соидальное приближение.
Для работы с синусоидальной регрессией в системе Mathcad
предусмотрена функция
sinfit(VX, VY, Guess)
где VX и VY – векторы значений, а Guess – так же как и в экс-
поненциальной регрессии вектор начальных значений.
Приведём пример.
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
66
Рис. 5.4.1. Построение синусоидальной регрессии
Однако этой функцией не всегда можно пользоваться, так как
нельзя задавать коэффициент при
x
(Рис. 5.4.2).
Пример ниже.

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
67
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
68
Рис. 5.4.2. Ошибка в построении синусоидальной регрессии
В этом случае можно пользоваться регрессией общего вида
(см. 5.5), при этом подбирая коэффициенты у функций. (Рис. 5.4.3)
Рис. 5.4.3. Построение синусоидальной регрессии с применением
функции регрессии общего вида
5.5. ЛИНЕЙНАЯ РЕГРЕССИЯ ОБЩЕГО ВИДА
В Mathcad реализована возможность выполнения линейной
регрессии общего вида. При ней заданная совокупность точек при-
ближается к функции вида:
...)(22)(11),...,2,1,(
xFKxFKKnKKxF
)(... xFnKn
.

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
69
Таким образом, функции регрессии является линейной комби-
нацией функций )(1 xF , )(2 xF , … )(xFn , причём сами эти функ-
ции могут быть нелинейными, что резко расширяет возможности
такой аппроксимации и распространяет её на многие нелинейные
функции.
Для реализации линейной регрессии общего вида используется
такая функция системы Mathcad, как
linfit(VX, VY, F),
которая возвращает вектор коэффициентов K линейной регрес-
сии общего вида, при котором среднеквадратичная погрешность
приближения «облака» исходных точек, координаты которых хра-
нятся в векторах VX и VY, оказывается минимальной.
Вектор F должен содержать функции )(1 xF , )(2 xF , …
)(xFn , записанные в символьном виде. Приведём пример (Рис.
5.5.1).
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
70
Рис. 5.5.1. Пример построение регрессии общего вида
Большой недостаток этого способа заключается в том, что не-
обходимо самому подбирать ту совокупность функции, на которую
по мнению читателя «похоже» «облако» значений. В данном слу-
чае Mathcad только ищет коэффициенты, которые стоят перед
функциями (рис. 5.5.2).
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
71
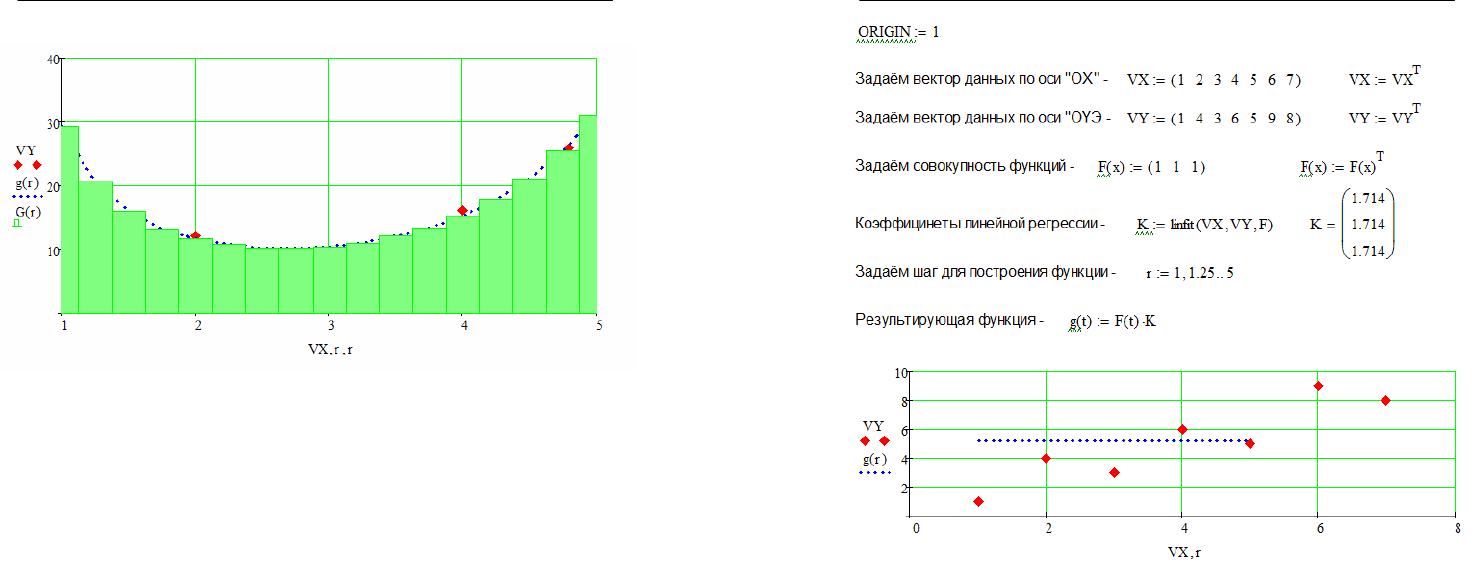
Рис. 5.5.2. Пример построение регрессии общего вида
Рассмотрим такой пример построения линейной регрессии при
помощи функции регрессии общего вида (Рис. 5.5.3)
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
72
Рис. 5.5.3 (а). Пример построения линейной регрессии
при помощи функции регрессии общего вида
В данном случае было бы разумно, если программа находила
бы линейную регрессию, однако, как было сказано выше, она ищет
только коэффициенты перед теми функциями, которые сам задаёт
пользователь. В данном случае программа просто выдала средний
результат.

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
73
Рис. 5.5.3 (б). Пример построения линейной регрессии
при помощи функции регрессии общего вида
После того как была задана линейная функция, программа на-
шла соответствующий коэффициент при переменной
x
. Т.е. в
уравнении bkxxy
)( этот коэффициент
k
.
Также обратите внимание на то, что функция начинается не из
начала координат. Здесь программа «нашла» второй коэффициент
при второй функции в векторе функций равный 0,429. Другими
словами, программа «подняла» график для того, чтобы приближе-
ние было как можно точнее.
А в следующем примере мы зададим вторую функцию в столб-
це функций 0)(
2
xF . При этом результирующая функция будет
выходить из начала координат. Но при этом изменятся другие ко-
эффициенты.
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
74
Рис. 5.5.3 (в). Пример построения линейной регрессии
при помощи функции регрессии общего вида
Таким образом, нахождение регрессии общего вида при помо-
щи этой функции является относительно сложным занятием, одна-
ко при правильном нахождении комбинации функций, результат
будет достаточно точным. В данном случае можно дать несколько
советов по подбору функций.
Во-первых, создавайте всегда матрицу функций по меньшей
мере 5 функций. В самом крайнем случае оставшиеся ячейки мож-
но записать в виде нулевой функции и она не окажет ни какого
влияния на результат. Во-вторых, применяйте единичную функ-
цию – она позволит «регулировать» положение результирующей
функции относительно оси
OX
.
Ниже рассмотрим ещё один пример построение регрессии эле-
ментарной функции при помощи функции построения регрессии
общего вида (Рис. 5.5.4)

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
75
Рис. 5.5.4 (а). Пример построения квадратичной регрессии
при помощи функции регрессии общего вида
Если мы в вектор функций добавим единичную функцию, то
график результирующей функции «подвинется».
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
76
Рис. 5.5.4 (б). Пример построения квадратичной регрессии
при помощи функции регрессии общего вида

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
77
6. ПРИМЕРЫ РЕШЕНИЯ КОНТРОЛЬНЫХ РАБОТ
1. Случайная величина Х ~ Bi(5; 1/4). Найти наиболее и наиме-
нее вероятные значения Х.
РЕШЕНИЕ
СВ распределена по биномиальному закону с параметрами n =
6 и p = ¼ и принимает значения 0, 1, 2, 3, 4, 5. Вычислим вероятно-
сти реализаций с помощью формулы Бернулли:
;237,0
4
3
)1(}0{
5
5
pXP
;396,0
4
3
4
1
5)1(}1{
4
4
pnpXP
;264,0
4
3
4
1
!3!2
!5
)1(}2{
32
322
5
ppCXP
;088,0
4
3
4
1
!2!3
!5
)1(}3{
23
233
5
ppCXP
;014,0
4
3
4
1
5)1(}4{
4
4
pnpXP
.001,0
4
1
}5{
5
5
pXP
Очевидно, что наиболее вероятное значение СВ – Х = 1, наи-
менее вероятное – Х = 5.
Ниже приведём решения данной задачи в системе Mathcad.
При решении этой задачи используется функция ряда биноми-
ального распределения – dbinom(k, n, p).
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
78

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
79
Пример решения задачи №1 в системе Mathcad
2. За время эксплуатации автомобиля в среднем случается 4
прокола на 100 000 км. Число проколов описывается распределе-
нием Пуассона. Рассчитать вероятность того, что за 150 000 км
случится не более одного прокола.
РЕШЕНИЕ
Если за 100 000 км в среднем случается 4 прокола, то за 150
000 их будет 6. Следовательно, число проколов за 150 000 км оп-
ределяется СВ с распределением Пуассона с параметром а = 6.
Интересующая нас вероятность равна вероятности возникно-
вения 0 или 1 прокола. По формуле для распределения Пуассона
получаем:
.017,0
!
1
6
!
0
6
}1{}0{
6
1
6
0
eeXPXPP
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
80
3. Величина промаха при стрельбе описывается нормальным
законом распределения. Средний промах составляет 10 см. Какова
вероятность совершить промах более 7 см?
РЕШЕНИЕ
