Денисов-Винский Н.Д. Mathcad при решении задач по Высшей математики. 3 курс
Подождите немного. Документ загружается.


Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
21
Рис. 3.1.2. Построение графиков плотности распределения и функции распре-
деления по биномиальному закону (при n = 3 и p = 0,6)
Теперь рассмотрим решение той же самой задачи при количе-
стве мишеней равном пяти и вероятности попадания в каждую p =
0,73. Проследим, как изменятся графики.
Решим эту задачу при помощи специальных функций системы
Mathcad (Рис. 3.1.3.).
Рис. 3.1.3 (а). Построение ряда распределения и функции распределения
по биномиальному закону (при n = 5 и p = 0,73)
Далее построим график функции плотности распределения и
график функции распределения.
Найдём математическое ожидание и дисперсию.
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
22

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
23
Рис. 3.1.3 (б). Построение графиков ряда распределения и функции рас-
пределения по биномиальному закону (при n = 5, p= 0,73)
3.2. РАСПРЕДЕЛЕНИЕ ПУАССОНА
Дискретная случайная величина X, принимающая значения k =
0,1, ..., имеет распределение Пуассона с параметром а > 0, что сим-
волически записывается как X ~ П(а), если ее ряд распределения
задается формулой
.
!
}{
a
k
e
k
a
kXP
Математическое ожидание и дисперсия для распределения Пу-
ассона одинаковы и равны а: m
х
= d
x
= a.
Распределение Пуассона широко используется в теории массо-
вого обслуживания.
Приведем пример типичной ситуации.
Пусть на телефонную станцию в произвольные моменты време-
ни случайным образом поступают заявки так, что выполняются три
условия:
а) вероятность появления любого количества заявок за какой-
либо отрезок времени не зависит от того, сколько их поступило за
любой другой, не пересекающийся с ним отрезок, т.е. заявки рас-
пределяются на оси времени независимо друг от друга. Это усло-
вие независимости;
б) вероятность появления за достаточно малый интервал време-
ни ∆t двух и более заявок пренебрежимо мала по сравнению с ве-
роятностью поступления в течение этого интервала времени одной
заявки. Это условие ординарности;
в) вероятность появления фиксированного числа заявок в ин-
тервале времени зависит лишь от длины этого интервала, но не за-
висит от его расположения на оси времени. Это условие стацио-
нарности.
В данном случае случайная величина X, равная числу заявок,
поступивших на телефонную станцию за единицу времени, имеет
распределение П(а), где a — среднее число заявок, поступающих в
единицу времени. Теоретически, прийти может любое число зая-
вок, но наиболее вероятное значение равно среднему!
Пример.
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
24
В магазин в среднем заходят 3 покупателя за 5 минут. Какова
вероятность, что в ближайшие 5 минут в магазин зайдут 5 покупа-
телей?
Решение
Поток покупателей описывается распределением Пуассона с
параметром а = 3. Таким образом, искомая вероятность равна ве-
роятности реализации k = 5 для случайной величины П(3):
.1,0
!
5
3
}5{
3
5
eXP
В системе Mathcad ряд распределения Пуассона описывается сле-
дующей функцией
dpois(k, λ)
где k – целое не отрицательное число, которое может выступать
как счётчик по графику плотности распределения, λ - неотрица-
тельный параметр распределения Пуассона.
Наравне с рядом распределения Пуассона, в системе Mathcad
есть также функция распределения Пуассона. Она записывается
следующим образом:
ppois(k, λ)
Так же как и в ряду распределения Пуассона, здесь k – целое не
отрицательное число, которое может выступать как счётчик по гра-
фику плотности распределения, λ - неотрицательный параметр
распределения Пуассона.
Теперь наглядно рассмотрим, как меняется характер ряда рас-
пределения в зависимости от параметра a.
Построим в системе Mathcad несколько таких распределений
(рис. 3.2.1).
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
25
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
26
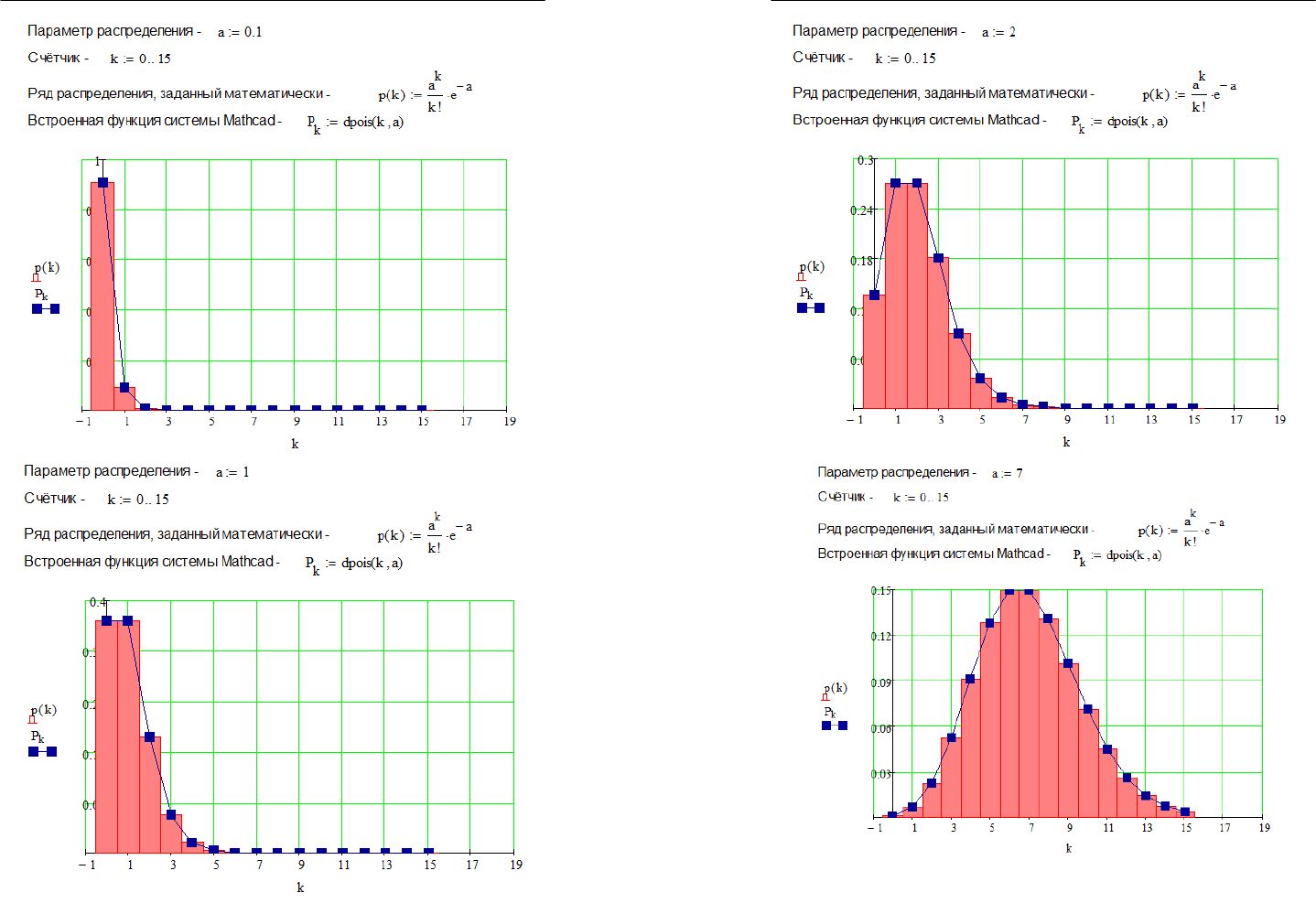
Рис. 3.2.1. Построение ряда распределения Пуассона в зависимости от
параметра распределения
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
27
Применительно к выше поставленной задаче с покупателем в
магазине, коэффициент распределения a = 3, так как это есть сред-
няя величина (она же равняется и дисперсии и математическому
ожиданию), при этом интересующее нас количество покупателей
равно 5.
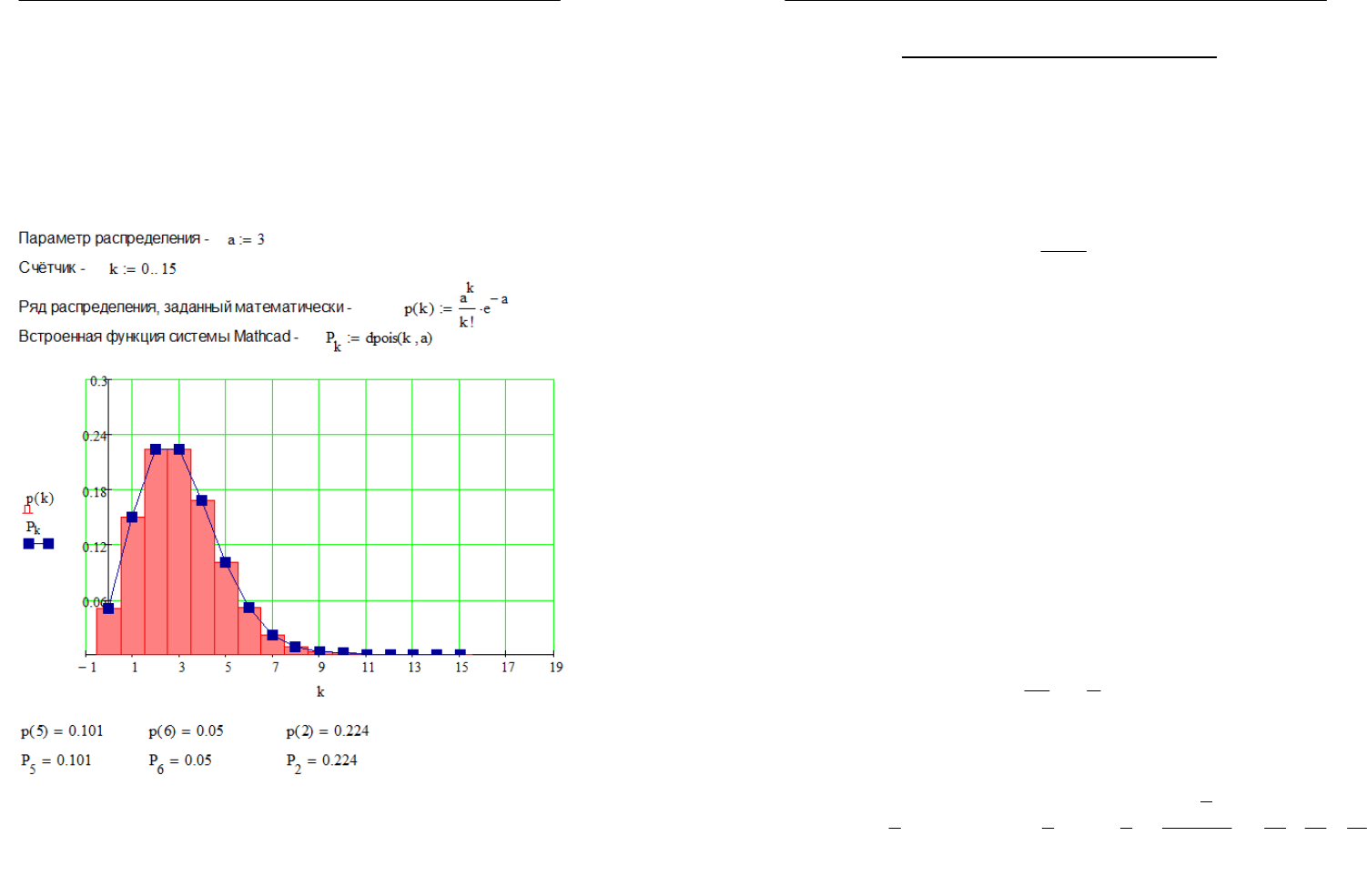
Построив это распределение можно также определить вероят-
ность того, зайдёт ли в ближайшее время в магазин шесть покупа-
телей или два покупателя (Рис. 4.2.2.).
Рис. 3.2.2. Решение задачи с применением ряда
распределения Пуассона
Разберём несколько непрерывных распределений, которые так-
же широко встречаются на практике.
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
28
3.3. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ
Равномерное распределение является простейшим среди не-
прерывных распределений. Для простоты будем рассматривать
случайные величины, равномерно распределенные на отрезке.
Случайная величина Х распределена равномерно на отрезке
[a,b] (Х~R(a,b)), если плотность вероятности имеет вид
].,[,0
],,[,
1
)(
bax
bax
ab
xf
Если случайная величина распределена равномерно на отрезке,
то вероятность ее попадания в какой-либо внутренний интервал
зависит лишь от длины интервала, а не от его расположения внут-
ри отрезка. Другими словами, попадание в любую точку отрезка
равновероятно.
Для примера вычислим математическое ожидание и дисперсию
случайно величины Х~R(0,1), т. е. равномерно распределенной на
отрезке [0,1].
Ее плотность определяется формулой:
].1,0[,0
],1,0[,1
)(
x
x
xf
Математическое ожидание:
.
2
1
|
2
)(
1
0
2
1
0
x
dxxdxxxfm
x
Дисперсия:
.
12
1
24
1
24
1
|
3
2
1
2
1
2
1
)(
2
1
1
0
3
1
0
22
x
xdxdxxfxd
x

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
29
Замечания
Распределение R(0;1) используется для моделирования случай-
ных величин с произвольно заданным законом распределения.
Для работы с равномерным распределением в системе Mathcad
существует две функции – функция плотности и функция распре-
деления.
Синтаксис функции плотности равномерного распределения:
dunif(x, a, b)
где x – есть переменная для области распределения функции, a
и b – есть границы плотности.
Для функции равномерного распределения синтаксис функции
выглядит следующим образом:
punif(x, a, b)
внутренние переменные описываются аналогично.
Рис. 3.3.1. Пример применения функции dunif
При увеличении интервала высота графика функции т.е. её зна-
чения будет уменьшаться, так как площадь, которая ограничена
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
30
кривой графика функции и осью абсцисс должна равняться едини-
це.

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
31
Рис. 3.3.2. Пример применения функции dunif(), punif()
Читатель может обратить внимание, что в зависимости от изме-
нения граничных точек интервала меняется график функции рас-
пределения – меняется угол наклона кривой и плотности распреде-
ления – меняется максимум функции.
3.4. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Случайная величина Х имеет экспоненциальное (показатель-
ное) распределение с параметром λ > 0, если ее плотность вероят-
ности имеет вид
0,0
0,
)(
x
xе
xf
х
Функция распределения такой СВ Х ~ E(λ) имеет вид
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
32
0,0
0,1
)(
x
xе
xF
х
Математическое ожидание и дисперсия экспоненциально рас-
пределенной СВ определяются формулами:
;
1
X
m .
1
2
X
d
Экспоненциальное распределение является одним из основных
распределений, используемых в теории надежности.
Продолжительность безотказной работы многих технических
устройств, время технического обслуживания, а также время за-
держки вылета самолета по вине технических служб аэропорта
удовлетворительно описываются соответствующими экспоненци-
альными распределениями.
Экспоненциальное распределение в системе Mathcad описыва-
ется следующими функциями.
Функция плотности:
dexp(x, r)
где x – переменная, которая может быть задана либо дискретно,
либо непрерывно, причём она должна быть положительной, а r –
это параметр экспоненциального распределения. В курсе теории
вероятности переменная r обозначается
(смотрите выше) однако
в системе Mathcad он обозначается через r.
Функция распределения:
pexp(x, r)
аналогично с функцией плотности её параметры определяются
аналогично.
Две эти формулы могут выдавать либо дискретные значения,
либо непрерывные значения.

Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
33
Рассмотрим пример применения функции плотности экспонен-
циального распределения, а также саму функцию экспоненциаль-
ного распределения в системе Mathcad. Функцию отобразим дис-
кретно.
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
34
Ниже изобразим непрерывные функции плотности вероятно-
сти и распределение вероятности.
Рис. 3.4.1. Пример непрерывного задания функций распределения и
функции плотности распределения
Графики функции плотности распределения и функции распре-
деления вероятности могут изображаться как дискретно, так и не-
прерывно, в зависимости от задачи, которая поставлена. При изме-
нении параметра экспоненциального распределения в сторону уве-
личения, лучше использовать непрерывное отображение функций.
3.5. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Случайная величина Х имеет нормальное распределение с ма-
тематическим ожиданием m и дисперсией σ
2
> 0, т.е. Х ~ N(m; σ
2
),
если ее плотность выражается формулой
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
35
2
2
2
)(
2
1
)(
mx
exf .
Важно помнить внешний вид графика этой функции, зависи-
мость вида графика от параметров распределения и физический
смысл самого распределения.
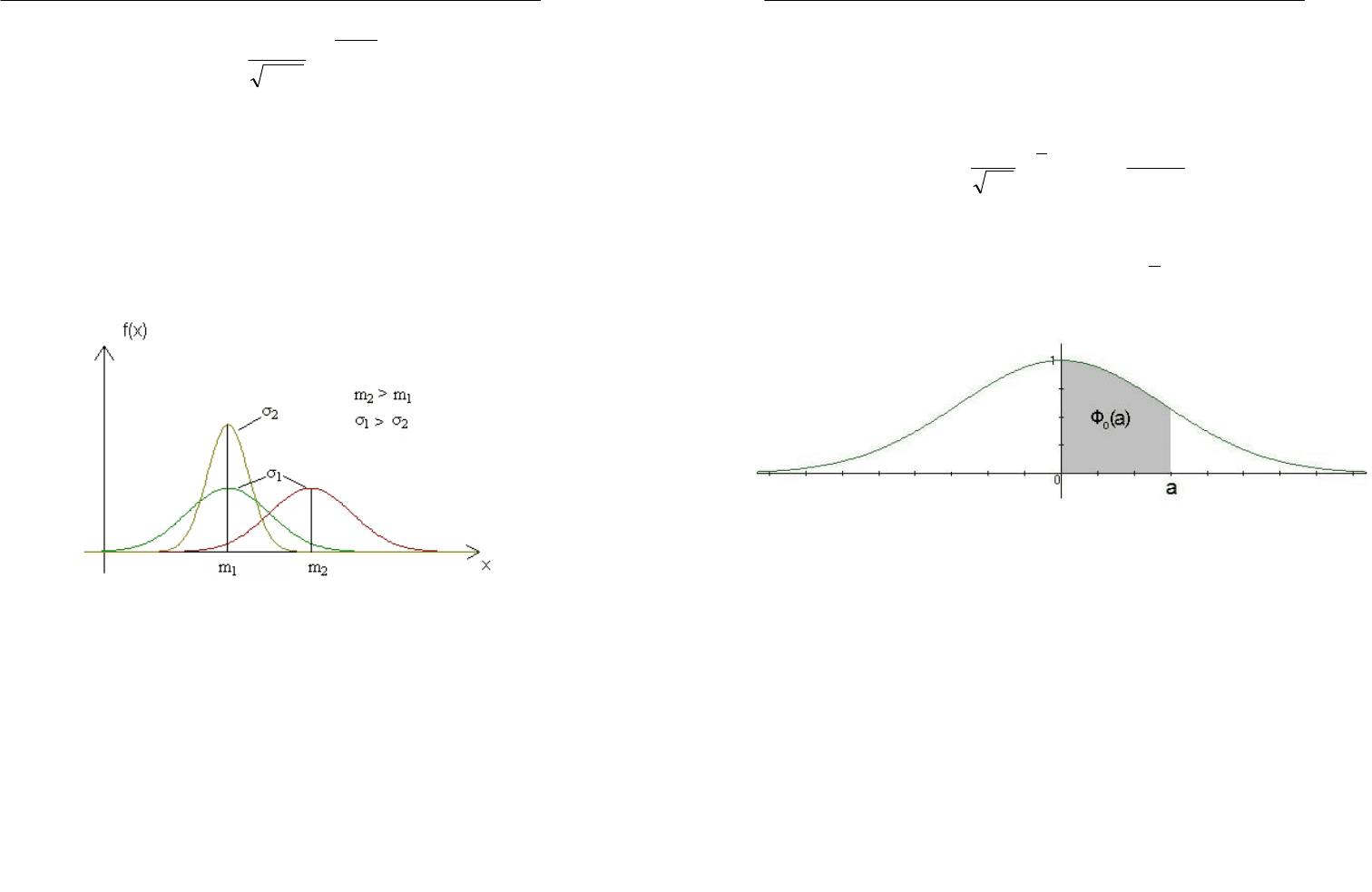
График плотности нормального распределения, называемый
кривой Гаусса (см. рис. 3.5.1).
Как видно, математическое ожидание m указывает на область
наиболее вероятных значений случайной величины. При измене-
нии m график плотности сдвигается вдоль оси Ох.
Рис. 3.5.1. Графики плотности нормального распределения
при различных значениях параметров
Дисперсия σ
2
"отвечает" за разброс значений случайной вели-
чины вокруг ее математического ожидания. Если она мала, то зна-
чения сконцентрированы вокруг m – "крутой пик" (σ
1
). Чем дис-
персия выше, тем равномернее распределена СВ, "холм" пологий
(σ
2
).
Нормальное распределение имеет широкое распространение в
прикладных задачах. Например, ошибки измерений распределены
по нормальному закону. Никакой прибор никогда не выдаст точное
значение измеряемой величины, неизбежны ошибки в ту или иную
сторону. Результат измерения является случайной величиной. Чем
хуже прибор, тем больше дисперсия, т. е. ошибка измерений.
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
36
Важное значение имеет распределение с классическими пара-
метрами m = 0, σ
2
= 1 - N(0,1), называемое стандартным нор-
мальным распределением. Распределения с другими параметрами
получаются из него простейшими арифметическими операциями.
Плотность N(0,1) – функция
2
2
2
1
)(
t
etf
, где
x
mx
t
.
Вероятность того, что СВ N(0,1) принимает значение от 0 до y
определяется функцией Лапласа. dteaФ
a t
0
2
0
2
)( .
Рис. 3.5.1. Функция Лапласа
Для работы с нормальным распределением в системе Mathcad
определены следующие функции.
Функция плотности нормального распределения:
dnorm(x, μ, σ)
где x – есть переменная величина функции (может задаваться
как дискретно, так и непрерывно), μ –математическое ожидание и
σ – среднеквадратичное отклонение, которое должно быть всегда
больше ноля.
Функция распределения:
pnorm(x, μ, σ)
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
37
аналогично функции плотности нормального распределения x –
есть переменная величина функции, μ – среднее значение, оно же
математическое ожидание и σ – среднеквадратичное отклонение,
которое должно быть всегда больше ноля.
Рассмотрим эти функции (Рис. 3.5.2.).
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
38
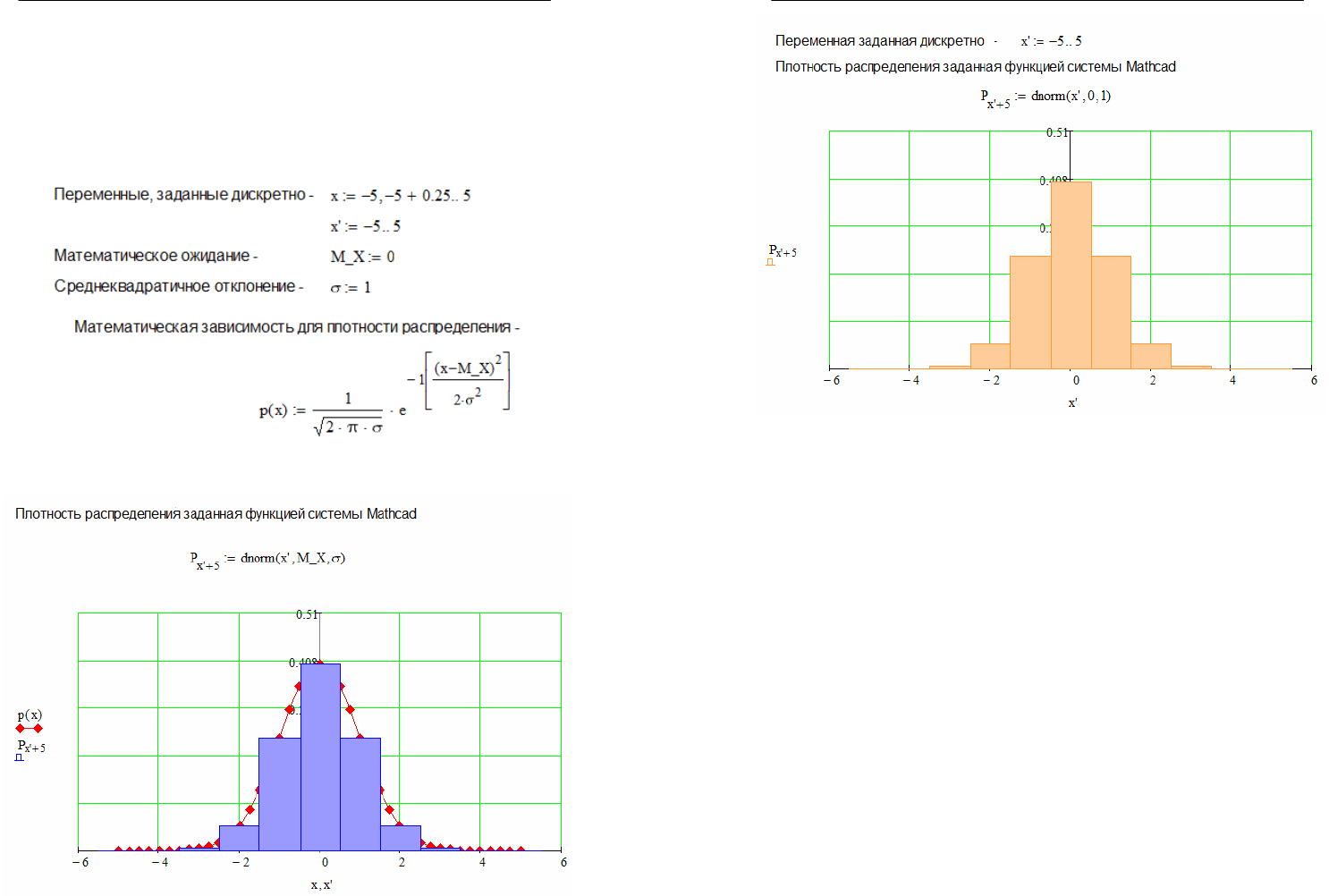
Рис. 3.5.2. Пример применения функций dnorm()
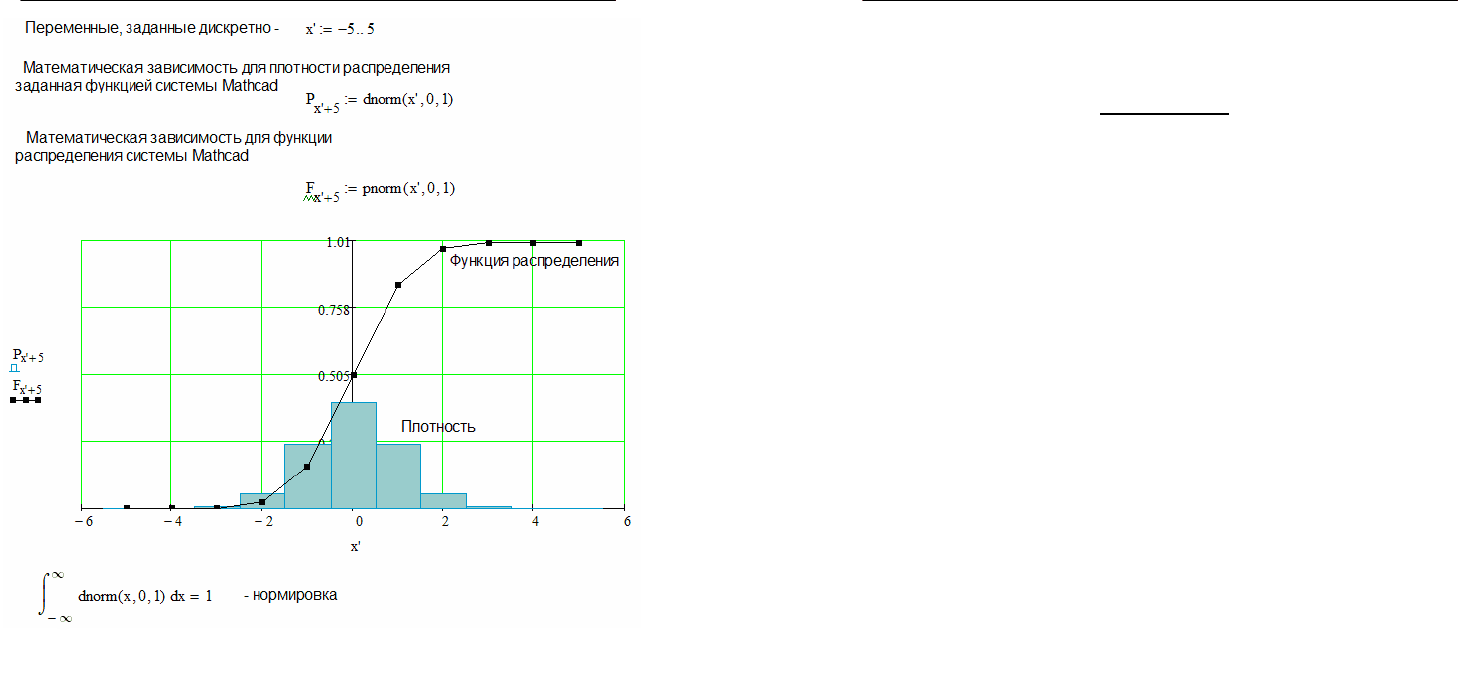
Рассмотрим пример функции плотности нормального распреде-
ления и функцию распределения (Рис. 3.5.3.).
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
39
Рис. 3.5.3. Функция плотности нормального распределения и
функция распределения
Автор: Денисов-Винский Н.Д.
E-mail: denisov.vinskiy@yandex.ru
40
4. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
4.1. ВЫБОРКА
Математическая статистика – наука о математических методах,
позволяющая по статистическим данным (реализациям случайной
величины) построить модель исследуемого явления (например,
плотность случайной величины).
Можно сказать, задачи математической статистики обратны
задачам теории вероятностей. Теория вероятностей, зная законы
распределения случайной величины, пытается ответить на вопросы
об их реализациях. Математическая статистика, наоборот, по из-
вестным реализациям пытается определить законы распределения
СВ.
Ключевым объектом для изучения в математической статисти-
ке является выборка.
Выборкой называется вектор Z
n
= (x
1
, x
2
, …, x
n
), компонентами
которого являются реализации некоторой случайной величины.
Например, если в течение недели каждый день в одно и то же
время замерять напряжение в сети (случайная величина!), то такая
выборка будет выглядеть примерно так: 215 В, 225 В, 217 В, 230 В,
228 В, 222 В, 210 В (в системе Mathcad она задана ниже – см. рис.
4.1.1.). Можно ли по этим данным сказать что-то определенное о
распределении случайной величины, ее математическом ожидании
и дисперсии? В этом и состоит задача математической статистики.
Разумеется, чем больше выборка, тем точнее можно ответить на
заданные вопросы.
Рассмотрим, как в системе Mathcad можно задать выборку.
Во-первых, покажем, что уже существующая выборка - допус-
тим это измерение температуры нагрева обмотки двигателя – мо-
жет быть представлена в среде Mathcad как матрица-строка, т.е.
вектор. При таком способе задания создаётся матрица-строка не-
обходимого количества элементов. Это удобно с точки зрения
дальнейшей работы с этими данными - анализа данных, нахожде-
ния математического ожидания и дисперсии.
Ниже приведён пример задания выборки в системе Mathcad.
