Дементьев Ю.И., Самохин А.В., Жулёва Л.Д., Шевелёва В.Н. Сборник задач по высшей математике. Интегралы. Дифференциальные уравнения
Подождите немного. Документ загружается.

úÁÄÁÞÉ ÄÌÑ ÓÁÍÏÓÔÏÑÔÅÌØÎÏÇÏ ÒÅÛÅÎÉÑ 51
320. xy = −2, y = x −3;
321. xy = 4, x = 4, y = 4, x = 0, y = 0;
322. ËÁÒÄÉÏÉÄÏÊ ρ = a(1 + cos ϕ);
323. ρ = a cos 2ϕ;
324. ρ = a sin 2ϕ;
325. ρ = 2 + sin 2ϕ;
326. ρ = ae
ϕ
, ÇÄÅ 0 6 ϕ 6 2π;
327. ρ = a sin 3ϕ;
328. ρ = a cos 3ϕ;
329. ÏÄÎÏÊ ÁÒËÏÊ ÃÉËÌÏÉÄÙ x = a(t − sin t), y = a(1 − cos t), 0 6 t 6 2π É
ÏÓØÀ OX;
330. ρ = a cos 4ϕ;
331. ρ = a sin 4ϕ.
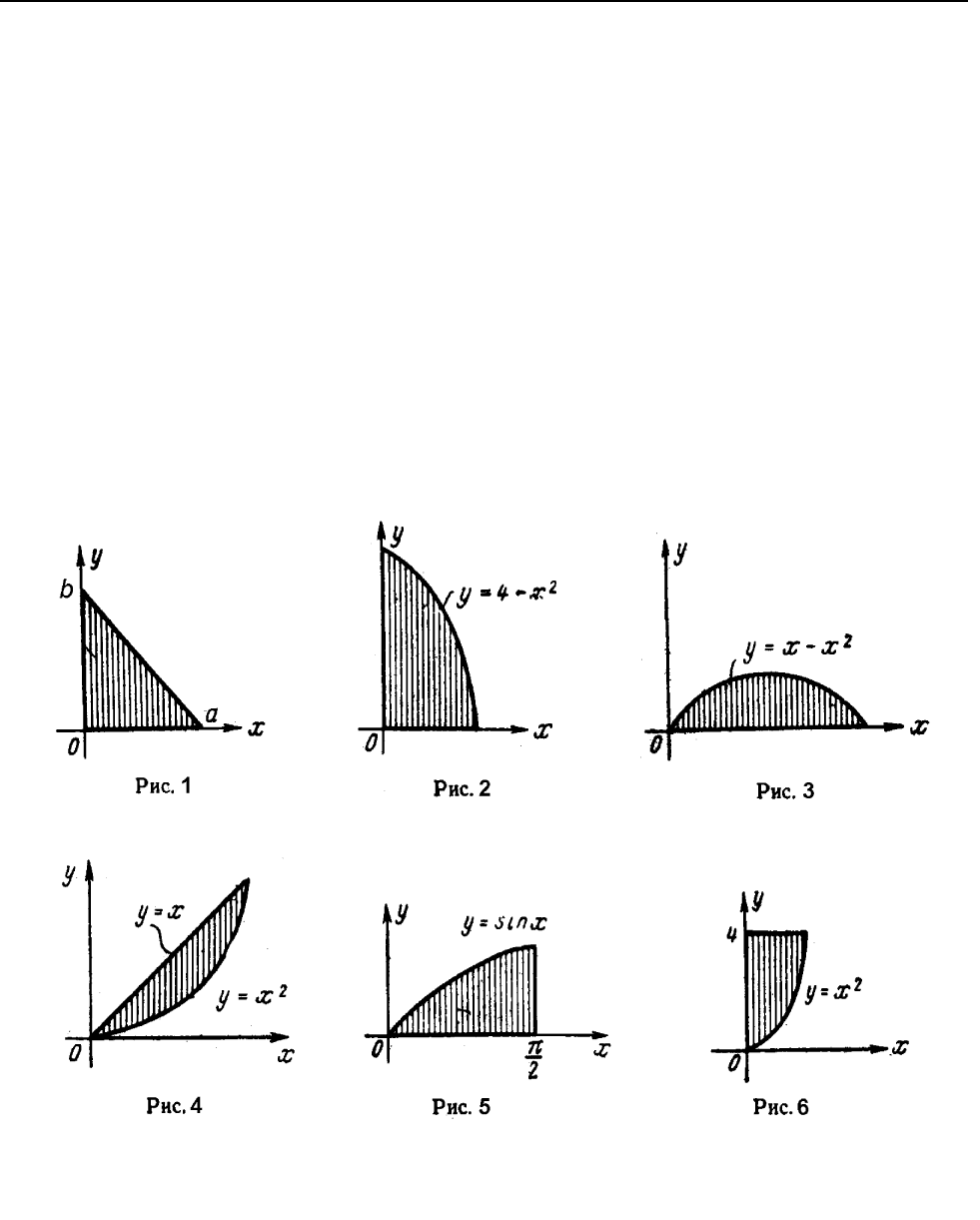
332. ÷ÙÞÉÓÌÉÔØ ÐÌÏÝÁÄÉ ÆÉÇÕÒ, ÉÚÏÂÒÁÖÅÎÎÙÈ ÎÁ ÒÉÓÕÎËÁÈ 1 ¡ 6.
÷ÙÞÉÓÌÉÔØ ÏÂßÅÍÙ ÔÅÌ, ÏÂÒÁÚÏ×ÁÎÎÙÈ ×ÒÁÝÅÎÉÅÍ ÆÉÇÕÒÙ, ÏÇÒÁÎÉÞÅÎÎÏÊ
ÌÉÎÉÑÍÉ:
333. y = 4 − x
2
, y = 0, x = 0, ÇÄÅ x > 0 ×ÏËÒÕÇ: 1) ÏÓÉ x, 2) ÏÓÉ y;
334. y = x −x
2
, y = 0 ×ÏËÒÕÇ ËÁÖÄÏÊ ÉÚ ÓÌÅÄÕÀÝÉÈ ÐÒÑÍÙÈ: 1) y = 0, 2)
x = 0, 3) x = 2, 4) x = −2, 5) y = −1, 6) y = 2;
335. y = e
x
, x = 0, x = 1, y = 0 ×ÏËÒÕÇ: 1) ÏÓÉ x, 2) ÏÓÉ y;
336. y = x
2
, y = 4, x = 0, ÇÄÅ x > 0 ×ÏËÒÕÇ: 1) ÏÓÉ x, 2) ÏÓÉ y;

52 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
337. y = x
2
+ 1, y = 0, x = 1, x = 2 ×ÏËÒÕÇ: 1) ÏÓÉ x, 2) ÏÓÉ y;
338. y = x
3
, y = 1, x = 0 ×ÏËÒÕÇ: 1) ÏÓÉ x, 2) ÏÓÉ y;
339.
x
2
a
2
+
y
2
b
2
= 1, y = 0, ÇÄÅ y > 0 ×ÏËÒÕÇ ÏÓÉ x;
340. y = ln x, y = 0, x = e ×ÏËÒÕÇ ËÁÖÄÏÊ ÉÚ ÓÌÅÄÕÀÝÉÈ ÐÒÑÍÙÈ: 1)
y = 0, 2) x = 0, 3) y = −1, 4) x = 1, 5) x = −1, 6) y = 1;
341. y = sin x, y = 0, ÇÄÅ 0 6 x 6 π ×ÏËÒÕÇ ËÁÖÄÏÊ ÉÚ ÓÌÅÄÕÀÝÉÈ ÐÒÑÍÙÈ:
1) y = 0, 2) x = 0, 3) x = 2π, 4) x = −1, 5) x = −2, 6) y = 1, 7) y = −2;
342. x
2
− y
2
= 4, y = 2, y = 0 ×ÏËÒÕÇ ÏÓÉ x;
343. y = x, y = x
2
×ÏËÒÕÇ: 1) ÏÓÉ x, 2) ÏÓÉ y;
344. y = cos 2x, y = 0, x = 0, ÇÄÅ 0 6 x 6
π
4
×ÏËÒÕÇ: 1) ÏÓÉ x, 2) ÏÓÉ y;
345. y = sin x, y = 0, ÇÄÅ 2π 6 x 6 3π ×ÏËÒÕÇ ËÁÖÄÏÊ ÉÚ ÓÌÅÄÕÀÝÉÈ
ÐÒÑÍÙÈ: 1) y = 0, 2) x = 0, 3) x = π, 4) y = −2;
346. y = 2x − x
2
, y = 0 ×ÏËÒÕÇ ËÁÖÄÏÊ ÉÚ ÓÌÅÄÕÀÝÉÈ ÐÒÑÍÙÈ: 1) x = 0,
2) y = 0, 3) x = −1, 4) y = 1;
347. y =
4
x
, x = 1, x = 4, y = 0 ×ÏËÒÕÇ: 1) ÏÓÉ x, 2) ÏÓÉ y;
348. y =
1
1+x
2
, x = 1, x = −1, y = 0 ×ÏËÒÕÇ: 1) ÏÓÉ x, 2) ÏÓÉ y.
÷ÙÞÉÓÌÉÔØ ÄÌÉÎÕ ÄÕÇÉ ËÒÉ×ÏÊ:
349. y
2
= x
3
, ÏÔÓÅÞÅÎÎÏÊ ÐÒÑÍÏÊ x = 1;
350. y = ln cos x, ÏÔÓÅÞÅÎÎÏÊ ÐÒÑÍÙÍÉ x = 0, x =
π
6
;
351. y
2
= (x + 1)
3
, ÏÔÓÅÞÅÎÎÏÊ ÐÒÑÍÏÊ x = 4;
352. y
2
=
4
9
(2 − x)
3
, ÏÔÓÅÞÅÎÎÏÊ ÐÒÑÍÏÊ x = −1;
353. y =
a
2
(e
x
a
+ e
−
x
a
) ÍÅÖÄÕ ÏÓØÀ y É ÐÒÑÍÏÊ x = a;
354. y = x
2
− 1, ÏÔÓÅÞÅÎÎÏÊ ÏÓØÀ x;
355. y = ln sin x ÏÔ x =
π
3
ÄÏ x =
2π
3
;
356. ÁÓÔÒÏÉÄÙ x = a cos
3
t, y = a sin
3
t;
357. ÏÄÎÏÊ ÁÒËÉ ÃÉËÌÏÉÄÙ x = a(t − sin t), y = a(1 − cos t), 0 6 t 6 2π;
358. ËÁÒÄÉÏÉÄÙ r = 4(1 − cos ϕ);
359. ÐÅÒ×ÏÇÏ ÚÁ×ÉÔËÁ ÓÐÉÒÁÌÉ r = aϕ, 0 6 ϕ 6 2π;
360. y =
x
2
4
−
1
2
ln x ÏÔ x = 1 ÄÏ x = e.
§3. îÅÓÏÂÓÔ×ÅÎÎÙÅ ÉÎÔÅÇÒÁÌÙ
3.1. îÅÓÏÂÓÔ×ÅÎÎÙÅ ÉÎÔÅÇÒÁÌÙ Ó ÂÅÓËÏÎÅÞÎÙÍÉ ÐÒÅÄÅÌÁÍÉ
ðÕÓÔØ ÆÕÎËÃÉÑ f(x) ÏÐÒÅÄÅÌÅÎÁ ÎÁ ÐÒÏÍÅÖÕÔËÅ [a, +∞) É ÉÎÔÅÇÒÉÒÕÅÍÁ
× ÌÀÂÏÊ ËÏÎÅÞÎÏÊ ÅÇÏ ÞÁÓÔÉ [a, A], ÔÁË ÞÔÏ ÉÎÔÅÇÒÁÌ
A
R
a
f(x) dx ÉÍÅÅÔ ÓÍÙÓÌ
ÐÒÉ ÌÀÂÏÍ A > a.

§3. îÅÓÏÂÓÔ×ÅÎÎÙÅ ÉÎÔÅÇÒÁÌÙ 53
ïÐÒÅÄÅÌÅÎÉÅ 1. îÅÓÏÂÓÔ×ÅÎÎÙÍ ÉÎÔÅÇÒÁÌÏÍ ÏÔ ÆÕÎËÃÉÉ f(x) ÐÏ ÐÒÏ-
ÍÅÖÕÔËÕ [a; +∞) ÎÁÚÙ×ÁÅÔÓÑ ÐÒÅÄÅÌ (ÅÓÌÉ ÏÎ ÓÕÝÅÓÔ×ÕÅÔ) lim
A→+∞
A
R
a
f(x) dx,
ÅÇÏ ×ÅÌÉÞÉÎÁ ÏÂÏÚÎÁÞÁÅÔÓÑ
+∞
Z
a
f(x) dx = lim
A→+∞
A
Z
a
f(x) dx. (1)
÷ ÓÌÕÞÁÅ, ÅÓÌÉ ÜÔÏÔ ÐÒÅÄÅÌ ËÏÎÅÞÅÎ, ÔÏ ÇÏ×ÏÒÑÔ, ÞÔÏ ÉÎÔÅÇÒÁÌ (1) ÓÈÏÄÉÔ-
ÓÑ, ÅÓÌÉ ÐÒÅÄÅÌ (1) ÂÅÓËÏÎÅÞÅÎ ÉÌÉ ×Ï×ÓÅ ÎÅ ÓÕÝÅÓÔ×ÕÅÔ, ÔÏ ÇÏ×ÏÒÑÔ, ÞÔÏ
ÉÎÔÅÇÒÁÌ ÒÁÓÈÏÄÉÔÓÑ.
ðÒÉÍÅÒ 1. òÁÓÓÍÏÔÒÉÍ ÉÎÔÅÇÒÁÌ
+∞
R
0
dx
1+x
2
. æÕÎËÃÉÑ f(x) =
1
1+x
2
ÎÁ ÌÀÂÏÍ
ÐÒÏÍÅÖÕÔËÅ [0, A] ÉÎÔÅÇÒÉÒÕÅÍÁ
+∞
Z
0
1
1 + x
2
dx = lim
A→+∞
A
Z
0
dx
1 + x
2
= lim
A→+∞
arctg A =
π
2
.
ðÏ ÏÐÒÅÄÅÌÅÎÉÀ ÉÎÔÅÇÒÁÌ ÓÈÏÄÉÔÓÑ É ÅÇÏ ×ÅÌÉÞÉÎÁ ÒÁ×ÎÁ
π
2
.
ðÒÉÍÅÒ 2. òÁÓÓÍÏÔÒÉÍ ÉÎÔÅÇÒÁÌ
+∞
R
0
sin x dx. æÕÎËÃÉÑ f (x) = sin x ÉÎ-
ÔÅÇÒÉÒÕÅÍÁ ÎÁ ÌÀÂÏÍ ÐÒÏÍÅÖÕÔËÅ [0, A]. ôÁË ËÁË
lim
A→+∞
A
Z
0
sin x dx = lim
A→+∞
(−cos A)
ÎÅ ÓÕÝÅÓÔ×ÕÅÔ, ÔÏ ÐÏ ÏÐÒÅÄÅÌÅÎÉÀ ÉÎÔÅÇÒÁÌ
+∞
R
0
sin x dx ÒÁÓÈÏÄÉÔÓÑ.
ðÒÉÍÅÒ 3. òÁÓÓÍÏÔÒÉÍ ÉÎÔÅÇÒÁÌ
+∞
R
1
dx
x
p
. æÕÎËÃÉÑ f (x) =
1
x
p
ÉÎÔÅÇÒÉÒÕ-
ÅÍÁ ÎÁ ÌÀÂÏÍ ÐÒÏÍÅÖÕÔËÅ [0, A]. ôÁË ËÁË
A
Z
1
dx
x
p
=
1
1−p
(A
1−p
− 1), p 6= 1,
ln A, p = 1,
ÔÏ ÉÎÔÅÇÒÁÌ
+∞
R
1
dx
x
p
ÓÈÏÄÉÔÓÑ ÐÒÉ p > 1 É ÒÁÓÈÏÄÉÔÓÑ ÐÒÉ p 6 1.
ó×ÏÊÓÔ×Á ÎÅÓÏÂÓÔ×ÅÎÎÏÇÏ ÉÎÔÅÇÒÁÌÁ.

54 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
1. åÓÌÉ ÓÕÝÅÓÔ×ÕÀÔ ÎÅÓÏÂÓÔ×ÅÎÎÙÅ ÉÎÔÅÇÒÁÌÙ ÏÔ ÆÕÎËÃÉÊ f (x) É g(x)
ÎÁ ÐÒÏÍÅÖÕÔËÅ [a; +∞), ÔÏ ÄÌÑ ÌÀÂÙÈ ÐÏÓÔÏÑÎÎÙÈ α É β ÓÐÒÁ×ÅÄÌÉ×Ï ÒÁ-
×ÅÎÓÔ×Ï:
+∞
Z
a
(αf(x) + βg(x)) dx = α
+∞
Z
a
f(x) dx + β
+∞
Z
a
g(x) dx.
2. ðÕÓÔØ a < c < +∞, É ÓÕÝÅÓÔ×ÕÅÔ ÎÅÓÏÂÓÔ×ÅÎÎÙÊ ÉÎÔÅÇÒÁÌ ÏÔ ÆÕÎËÃÉÉ
f(x) ÎÁ [a; +∞), ÔÏÇÄÁ
+∞
Z
a
f(x) dx =
c
Z
a
f(x) dx +
+∞
Z
c
f(x) dx.
3. ðÕÓÔØ ÆÕÎËÃÉÑ f(x) ÎÅÐÒÅÒÙ×ÎÁ ÎÁ ÐÒÏÍÅÖÕÔËÅ [a; +∞), ÔÏ ÄÌÑ ÌÀ-
ÂÏÊ ÓÔÒÏÇÏ ÍÏÎÏÔÏÎÎÏÊ É ÎÅÐÒÅÒÙ×ÎÏ ÄÉÆÆÅÒÅÎÃÉÒÕÅÍÏÊ ÎÁ [α; β) ÆÕÎËÃÉÉ
ϕ : [α; β) → [a; +∞) ÓÐÒÁ×ÅÄÌÉ×Ï ÒÁ×ÅÎÓÔ×Ï
+∞
Z
a
f(x) dx =
β
Z
α
f(ϕ(t))ϕ
0
(t) dt.
4. åÓÌÉ ÆÕÎËÃÉÉ f(x) É g(x) ÎÅÐÒÅÒÙ×ÎÏ ÄÉÆÆÅÒÅÎÃÉÒÕÅÍÙ ÎÁ [a; +∞)
É ÓÕÝÅÓÔ×ÕÅÔ lim
A→+∞
f(x)g(x), ÔÏ ÉÎÔÅÇÒÁÌÙ
+∞
R
a
f(x) dx É
+∞
R
a
g(x) dx ÏÄÎÏ-
×ÒÅÍÅÎÎÏ ÓÈÏÄÑÔÓÑ ÉÌÉ ÒÁÓÈÏÄÑÔÓÑ, É × ÓÌÕÞÁÅ ÉÈ ÓÈÏÄÉÍÏÓÔÉ ÉÍÅÅÔ ÍÅÓÔÏ
ÒÁ×ÅÎÓÔ×Ï
+∞
Z
a
f(x)g(x) dx = f(x)g(x)
+∞
a
−
+∞
Z
a
f
0
(x)g(x) dx.
úÁÍÅÞÁÎÉÅ. áÎÁÌÏÇÉÞÎÏ (1) ÏÐÒÅÄÅÌÑÅÔÓÑ ÉÎÔÅÇÒÁÌ ÏÔ ÆÕÎËÃÉÉ f(x) ÎÁ
(−∞; a]
a
Z
−∞
f(x) dx = lim
A→−∞
a
Z
A
f(x) dx,
ÒÁ×ÎÏ ËÁË É ÉÎÔÅÇÒÁÌ ÆÕÎËÃÉÉ f(x) ÎÁ ÐÒÏÍÅÖÕÔËÅ (−∞; +∞):
+∞
Z
−∞
f(x) dx = lim
B→−∞
A→+∞
A
Z
B
f(x) dx.

§3. îÅÓÏÂÓÔ×ÅÎÎÙÅ ÉÎÔÅÇÒÁÌÙ 55
ðÒÉÍÅÒ 4.
0
Z
−∞
dx
1 + x
2
= lim
A→−∞
0
Z
A
dx
1 + x
2
= lim
A→−∞
(−arctg A) =
π
2
.
ðÒÉÍÅÒ 5.
+∞
Z
−∞
dx
1 + x
2
=
+∞
Z
0
dx
1 + x
2
+
0
Z
−∞
dx
1 + x
2
= π.
3.2. îÅÓÏÂÓÔ×ÅÎÎÙÅ ÉÎÔÅÇÒÁÌÙ ÏÔ ÎÅÏÇÒÁÎÉÞÅÎÎÙÈ ÆÕÎËÃÉÊ
ðÕÓÔØ ÆÕÎËÃÉÑ f(x) ÚÁÄÁÎÁ ÎÁ ËÏÎÅÞÎÏÍ ÐÒÏÍÅÖÕÔËÅ [a; b], ÎÏ ÎÅÏÇÒÁ-
ÎÉÞÅÎÁ × ÜÔÏÍ ÐÒÏÍÅÖÕÔËÅ. ðÏÌÏÖÉÍ, ÞÔÏ × ÌÀÂÏÍ ÐÒÏÍÅÖÕÔËÅ [a; b − ε]
(0 < ε < b − a) f(x) ÏÇÒÁÎÉÞÅÎÁ É ÉÎÔÅÇÒÉÒÕÅÍÁ, ÎÏ ÏËÁÚÙ×ÁÅÔÓÑ ÎÅÏÇÒÁÎÉ-
ÞÅÎÎÏÊ × ËÁÖÄÏÍ ÐÒÏÍÅÖÕÔËÅ [b − ε, b]. ôÏÞËÁ b × ÜÔÏÍ ÓÌÕÞÁÅ ÎÁÚÙ×ÁÅÔÓÑ
ÏÓÏÂÏÊ ÔÏÞËÏÊ.
ïÐÒÅÄÅÌÅÎÉÅ 2. îÅÓÏÂÓÔ×ÅÎÎÙÍ ÉÎÔÅÇÒÁÌÏÍ ÏÔ ÆÕÎËÃÉÉ f(x) ÎÁ ÐÒÏ-
ÍÅÖÕÔËÅ [a, b] ÎÁÚÙ×ÁÅÔÓÑ ÐÒÅÄÅÌ lim
ε→0
b
R
a
f(x) dx, ÅÇÏ ×ÅÌÉÞÉÎÁ ÏÂÏÚÎÁÞÁÅÔÓÑ
b
Z
a
f(x) dx = lim
ε→0
b−ε
Z
a
f(x) dx. (2)
÷ ÓÌÕÞÁÅ, ÅÓÌÉ ÜÔÏÔ ÐÒÅÄÅÌ ËÏÎÅÞÅÎ, ÇÏ×ÏÒÑÔ, ÞÔÏ ÉÎÔÅÇÒÁÌ (2) ÓÈÏÄÉÔÓÑ.
åÓÌÉ ÖÅ ÐÒÅÄÅÌ (2) ÂÅÓËÏÎÅÞÅÎ ÉÌÉ ×Ï×ÓÅ ÎÅ ÓÕÝÅÓÔ×ÕÅÔ, ÔÏ ÇÏ×ÏÒÑÔ, ÞÔÏ
ÉÎÔÅÇÒÁÌ (2) ÒÁÓÈÏÄÉÔÓÑ.
úÁÍÅÞÁÎÉÅ. ÷ ÓÌÕÞÁÅ, ÅÓÌÉ f (x) ÏÇÒÁÎÉÞÅÎÁ É ÉÎÔÅÇÒÉÒÕÅÍÁ × ÌÀÂÏÍ
ÐÒÏÍÅÖÕÔËÅ [a + ε; b] É ÎÅÏÇÒÁÎÉÞÅÎÁ × ËÁÖÄÏÍ ÐÒÏÍÅÖÕÔËÅ [a; a + ε] ÓÐÒÁ×Á
ÏÔ ÔÏÞËÉ a (ÏÓÏÂÁÑ ÔÏÞËÁ), ÔÏÇÄÁ ÎÅÓÏÂÓÔ×ÅÎÎÙÊ ÉÎÔÅÇÒÁÌ ÆÕÎËÃÉÉ f(x) ÎÁ
ÐÒÏÍÅÖÕÔËÅ [a, b] ÏÐÒÅÄÅÌÑÅÔÓÑ ÒÁ×ÅÎÓÔ×ÏÍ
b
Z
a
f(x) dx = lim
ε→0
b
Z
a+ε
f(x) dx. (3)
úÁÍÅÞÁÎÉÅ. ðÕÓÔØ c ∈ [a, b] É ÆÕÎËÃÉÑ f(x) ÎÅÏÇÒÁÎÉÞÅÎÁ × ÔÏÞËÅ c,
ÐÒÉÞÅÍ ÎÁ ÐÒÏÍÅÖÕÔËÁÈ [a; c −ε
1
] (0 < ε
1
< c −a) É [c + ε
2
, b] (0 < ε
2
< b −c)
56 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
ÆÕÎËÃÉÑ f(x) ÉÎÔÅÇÒÉÒÕÅÍÁ, ÔÏÇÄÁ
b
Z
a
f(x) dx = lim
ε
1
→0
c−ε
1
Z
a
f(x) dx + lim
ε
2
→0
b
Z
c+ε
2
f(x) dx. (4)
ðÒÉÍÅÒ 6.
0
R
−1
dx
√
1−x
2
, x = −1 ¡ ÏÓÏÂÁÑ ÔÏÞËÁ.
0
Z
−1
dx
√
1 − x
2
= lim
ε→0
0
Z
−1+ε
dx
√
1 − x
2
= lim
ε→0
arcsin x
0
−1+ε
=
= lim
ε→0
(arcsin 0 − arcsin(−1 + ε)) = −arcsin(−1) =
π
2
.
éÎÔÅÇÒÁÌ ÓÈÏÄÉÔÓÑ É ÅÇÏ ×ÅÌÉÞÉÎÁ ÒÁ×ÎÁ
π
2
.
ðÒÉÍÅÒ 7.
1
R
0
dx
√
1−x
2
, x = 1 ¡ ÏÓÏÂÁÑ ÔÏÞËÁ.
1
Z
0
dx
√
1 − x
2
= lim
ε→0
1−ε
Z
0
dx
√
1 − x
2
=
= lim
ε→0
arcsin x
1−ε
0
= lim
ε→0
(arcsin(1 − ε) − arcsin 0) =
π
2
.
éÎÔÅÇÒÁÌ ÓÈÏÄÉÔÓÑ É ÅÇÏ ×ÅÌÉÞÉÎÁ ÒÁ×ÎÁ
π
2
.
ðÒÉÍÅÒ 8.
8
R
−1
dx
3
√
x
, x = 0 ¡ ÏÓÏÂÁÑ ÔÏÞËÁ.
8
Z
−1
dx
3
√
x
=
0
Z
−1
dx
3
√
x
+
8
Z
0
dx
3
√
x
= lim
ε
1
→0
0−ε
1
Z
−1
dx
3
√
x
+
+ lim
ε
2
→0
8
Z
0+ε
2
dx
3
√
x
= lim
ε
1
→0
3
2
· x
2/3
−ε
1
−1
+ lim
ε
2
→0
3
2
x
2/3
8
ε
2
=
=
3
2
(8
2/3
− (−1)
2/3
) =
3
2
· (4 − 1) =
9
2
.
úÁÄÁÞÉ ÄÌÑ ÓÁÍÏÓÔÏÑÔÅÌØÎÏÇÏ ÒÅÛÅÎÉÑ 57
ðÒÉÍÅÒ 9.
2
R
−2
2x dx
x
2
−1
, x = −1, x = 1 ¡ ÏÓÏÂÙÅ ÔÏÞËÉ.
2
Z
−2
2x dx
x
2
− 1
=
−1
Z
−2
2x dx
x
2
− 1
+
1
Z
−1
2x
x
2
− 1
dx +
2
Z
1
2x
x
2
− 1
dx =
= lim
ε
1
→0
−1−ε
1
Z
−2
dx
2
x
2
− 1
+ lim
ε
2
→0
ε
3
→0
1−ε
3
Z
−1+ε
2
dx
2
x
2
− 1
+ lim
ε
4
→0
2
Z
1+ε
4
dx
2
x
2
− 1
=
= lim
ε
1
→0
ln |x
2
− 1|
−1−ε
1
−2
+ lim
ε
2
→0
ε
3
→0
ln |x
2
− 1|
1−ε
3
−1+ε
2
+ lim
ε
4
→0
ln |x
2
− 1|
2
1+ε
4
= ∞.
éÎÔÅÇÒÁÌ ÒÁÓÈÏÄÉÔÓÑ.
ðÒÉÍÅÒ 10.
a
R
0
dx
(a−x)
p
, x = a ¡ ÏÓÏÂÁÑ ÔÏÞËÁ.
a
Z
0
dx
(a − x)
p
= lim
ε→0
a−ε
Z
0
dx
(a − x)
p
= lim
ε→0
a
Z
ε
dt
t
p
= lim
ε→0
1
1−p
(a
1−p
− ε
1−p
), p 6= 1
(ln a − ln ε), p = 1,
ÏÔÓÀÄÁ ÉÎÔÅÇÒÁÌ
a
R
0
dx
dx
(a − x)
p
ÓÈÏÄÉÔÓÑ, ÅÓÌÉ p < 1, É ÒÁÓÈÏÄÉÔÓÑ, ÅÓÌÉ p > 1.
úÁÍÅÞÁÎÉÅ. îÅÓÏÂÓÔ×ÅÎÎÙÅ ÉÎÔÅÇÒÁÌÙ ÏÔ ÎÅÏÇÒÁÎÉÞÅÎÎÙÈ ÆÕÎËÃÉÊ
ÏÂÌÁÄÁÀÔ ÔÅÍÉ ÖÅ Ó×ÏÊÓÔ×ÁÍÉ, ÞÔÏ É ÎÅÓÏÂÓÔ×ÅÎÎÙÅ ÉÎÔÅÇÒÁÌÙ ÎÁ ÂÅÓËÏ-
ÎÅÞÎÏÍ ÐÒÏÍÅÖÕÔËÅ. ðÒÉ ÉÈ ÆÏÒÍÕÌÉÒÏ×ËÅ ÐÒÏÍÅÖÕÔÏË [a; +∞) ÚÁÍÅÎÑÅÔÓÑ
ÎÁ ÐÒÏÍÅÖÕÔÏË [a, b].
úÁÄÁÞÉ ÄÌÑ ÓÁÍÏÓÔÏÑÔÅÌØÎÏÇÏ ÒÅÛÅÎÉÑ
÷ÙÞÉÓÌÉÔØ:
361.
+∞
R
0
e
−x
dx;
362.
+
∞
R
1
dx
x
α
;
363.
+∞
R
6
dx
x
2
−4x
;
364.
+∞
R
0
arcctg x dx;
58 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
365.
+∞
R
1
1+ln x
x
dx;
366.
+∞
R
0
sin x dx;
367.
0
R
−∞
xe
x
dx;
368.
1
R
0
dx
x
α
;
369.
3
R
0
dx
√
9−x
2
;
370.
1
R
0
ln x dx;
371.
1
R
0
ln
2
x dx;
372.
π
4
R
0
ctg x dx;
373.
2
R
0
dx
3
√
1−x
;
374.
3
R
0
dx
(x−3)
2
;
375.
6
R
2
dx
3
√
(4−x)
2
;
376.
π
2
R
0
dx
sin x
;
377.
+∞
R
0
dx
x
α
;
378.
+∞
R
0
e
−x
sin x dx.

çìá÷á II
äÉÆÆÅÒÅÎÃÉÁÌØÎÙÅ ÕÒÁ×ÎÅÎÉÑ
§4. ïÓÎÏ×ÎÙÅ ÐÏÎÑÔÉÑ ÔÅÏÒÉÉ ÄÉÆÆÅÒÅÎÃÉÁÌØÎÙÈ
ÕÒÁ×ÎÅÎÉÊ
4.1. úÁÄÁÞÉ, ÐÒÉ×ÏÄÑÝÉÅ Ë ÐÏÎÑÔÉÀ ÄÉÆÆÅÒÅÎÃÉÁÌØÎÏÇÏ ÕÒÁ×ÎÅ-
ÎÉÑ
÷Ï ÍÎÏÇÉÈ ÚÁÄÁÞÁÈ ÎÁÕËÉ É ÔÅÈÎÉËÉ ÔÒÅÂÕÅÔÓÑ ÎÁÈÏÄÉÔØ ÎÅÉÚ×ÅÓÔÎÕÀ
ÆÕÎËÃÉÀ, ËÏÔÏÒÁÑ ÕÄÏ×ÌÅÔ×ÏÒÑÅÔ ÕÒÁ×ÎÅÎÉÀ, Ó×ÑÚÙ×ÁÀÝÅÍÕ ÜÔÕ ÆÕÎËÃÉÀ,
ÅÅ ÐÒÏÉÚ×ÏÄÎÙÅ É ÎÅÚÁ×ÉÓÉÍÕÀ ÐÅÒÅÍÅÎÎÕÀ. ðÒÏÓÔÅÊÛÁÑ ÔÁËÁÑ ÚÁÄÁÞÁ
×ÓÔÒÅÞÁÌÁÓØ × ÉÎÔÅÇÒÁÌØÎÏÍ ÉÓÞÉÓÌÅÎÉÉ, ÇÄÅ ÎÁÈÏÄÉÌÉ ÆÕÎËÃÉÀ ÐÏ ÄÁÎÎÏÊ
ÅÅ ÐÒÏÉÚ×ÏÄÎÏÊ, ÔÏ ÅÓÔØ ÎÁÈÏÄÉÌÉ ÆÕÎËÃÉÀ, ÕÄÏ×ÌÅÔ×ÏÒÑÀÝÕÀ ÕÒÁ×ÎÅÎÉÀ
y
0
= f(x).
ðÒÉÍÅÒ 1. îÁÊÔÉ y, ÅÓÌÉ y
0
= x
3
.
òÅÛÅÎÉÅ. éÚ ÉÎÔÅÇÒÁÌØÎÏÇÏ ÉÓÞÉÓÌÅÎÉÑ ÍÙ ÚÎÁÅÍ, ÞÔÏ ÕÒÁ×ÎÅÎÉÀ y
0
=
= x
3
ÕÄÏ×ÌÅÔ×ÏÒÑÅÔ ÍÎÏÖÅÓÔ×Ï ÆÕÎËÃÉÊ y =
x
4
4
+ C, ÇÄÅ C ¡ ÐÒÏÉÚ×ÏÌØÎÁÑ
ÐÏÓÔÏÑÎÎÁÑ.
þÔÏÂÙ ÉÚ ÜÔÏÇÏ ÍÎÏÖÅÓÔ×Á ×ÙÄÅÌÉÔØ ÏÄÎÕ ÏÐÒÅÄÅÌÅÎÎÕÀ ÆÕÎËÃÉÀ, ÎÕÖÎÏ
ÚÁÄÁÔØ ÄÏÐÏÌÎÉÔÅÌØÎÏÅ ÕÓÌÏ×ÉÅ. îÁÐÒÉÍÅÒ, ÎÁÊÄÅÍ ÆÕÎËÃÉÀ, ËÏÔÏÒÁÑ ÐÒÉ
x = 1 ÐÒÉÎÉÍÁÅÔ ÚÎÁÞÅÎÉÅ y = 2, ÔÏ ÅÓÔØ y(1) = 2. ðÏÄÓÔÁ×ÌÑÑ x = 1, y = 2
× ÆÏÒÍÕÌÕ y =
x
4
4
+ C, ÐÏÌÕÞÉÍ 2 =
1
4
+ C. ïÔÓÀÄÁ C =
7
4
. óÌÅÄÏ×ÁÔÅÌØÎÏ,
ÆÕÎËÃÉÑ, ÕÄÏ×ÌÅÔ×ÏÒÑÀÝÁÑ ÕÒÁ×ÎÅÎÉÀ y
0
= x
3
É ÕÓÌÏ×ÉÀ y(1) = 2, ÉÍÅÅÔ
×ÉÄ y =
x
4
4
+
7
4
.
ðÒÉÍÅÒ 2. îÁÊÔÉ ËÒÉ×ÕÀ, ÏÂÌÁÄÁÀÝÕÀ ÔÅÍ Ó×ÏÊÓÔ×ÏÍ, ÞÔÏ ÏÔÒÅÚÏË ÌÀ-
ÂÏÊ ÅÅ ËÁÓÁÔÅÌØÎÏÊ, ÚÁËÌÀÞÅÎÎÏÊ ÍÅÖÄÕ ÏÓÑÍÉ ËÏÏÒÄÉÎÁÔ, ÄÅÌÉÔÓÑ ÐÏÐÏÌÁÍ
× ÔÏÞËÅ ËÁÓÁÎÉÑ.
òÅÛÅÎÉÅ. ðÕÓÔØ y = f(x) ¡ ÕÒÁ×ÎÅÎÉÅ ÉÓËÏÍÏÊ ËÒÉ×ÏÊ, M(x, y) ¡ ÐÒÏ-
ÉÚ×ÏÌØÎÁÑ ÔÏÞËÁ ÜÔÏÊ ËÒÉ×ÏÊ, Á AB ¡ ËÁÓÁÔÅÌØÎÁÑ Ë ËÒÉ×ÏÊ × ÔÏÞËÅ M.
õÇÏÌ, ÏÂÒÁÚÏ×ÁÎÎÙÊ ËÁÓÁÔÅÌØÎÏÊ Ó ÏÓØÀ Ox, ÏÂÏÚÎÁÞÉÍ ÞÅÒÅÚ ϕ. éÚ ÄÉÆÆÅ-
ÒÅÎÃÉÁÌØÎÏÇÏ ÉÓÞÉÓÌÅÎÉÑ ÍÙ ÚÎÁÅÍ, ÞÔÏ ÕÇÌÏ×ÏÊ ËÏÜÆÆÉÃÉÅÎÔ ËÁÓÁÔÅÌØÎÏÊ
Ë ËÒÉ×ÏÊ ÒÁ×ÅÎ
k = tg ϕ, tg(180
◦
− ϕ) =
P M
P A
⇒ tg ϕ = −
P M
AM
⇒ tg ϕ = −
y
x
(1)
59

60 çÌÁ×Á II. äÉÆÆÅÒÅÎÃÉÁÌØÎÙÅ ÕÒÁ×ÎÅÎÉÑ
É ÐÏÌÕÞÁÅÍ ÕÒÁ×ÎÅÎÉÅ
y
0
= −
y
x
, (2)
ËÏÔÏÒÏÅ Ó×ÑÚÙ×ÁÅÔ ÎÅÉÚ×ÅÓÔÎÕÀ ÆÕÎËÃÉÀ, ÅÅ ÐÒÏÉÚ×ÏÄÎÕÀ É ÎÅÚÁ×ÉÓÉÍÕÀ
ÐÅÒÅÍÅÎÎÕÀ.
ðÒÏ×ÅÒËÏÊ ÍÏÖÎÏ ÕÂÅÄÉÔØÓÑ, ÞÔÏ ÕÒÁ×ÎÅÎÉÀ (2) ÕÄÏ×ÌÅÔ×ÏÒÑÅÔ ÌÀÂÁÑ
ÆÕÎËÃÉÑ ×ÉÄÁ y =
C
x
. ôÁËÉÍ ÏÂÒÁÚÏÍ, ÍÙ ÐÏÌÕÞÉÌÉ ÓÅÍÅÊÓÔ×Ï ÇÉÐÅÒÂÏÌ.
îÁÊÄÅÍ ÇÉÐÅÒÂÏÌÕ, ËÏÔÏÒÁÑ ÐÒÏÈÏÄÉÔ ÞÅÒÅÚ ÔÏÞËÕ M
0
(2, 3). ðÏÄÓÔÁ×ÌÑÑ ËÏ-
ÏÒÄÉÎÁÔÙ ÔÏÞËÉ × ÆÏÒÍÕÌÕ y =
C
x
, ÐÏÌÕÞÉÍ 3 =
C
2
, C = 6. óÌÅÄÏ×ÁÔÅÌØÎÏ,
ÕÒÁ×ÎÅÎÉÅ ÇÉÐÅÒÂÏÌÙ, ÐÒÏÈÏÄÑÝÅÊ ÞÅÒÅÚ ÔÏÞËÕ M
0
(2, 3), ÉÍÅÅÔ ×ÉÄ
y =
6
x
.
ðÒÉÍÅÒ 3. çÒÕÚ, ÍÁÓÓÁ ËÏÔÏÒÏÇÏ m, ÚÁËÒÅÐÌÅÎ ÎÁ ×ÅÒÈÎÅÍ ËÏÎÃÅ ×ÅÒÔÉ-
ËÁÌØÎÏ ÒÁÓÐÏÌÏÖÅÎÎÏÊ ÐÒÕÖÉÎÙ (ÒÅÓÓÏÒÙ). åÇÏ ÏÔËÌÏÎÑÀÔ ÏÔ ÔÏÞËÉ O ÎÁ
ÎÅËÏÔÏÒÏÅ ÒÁÓÓÔÏÑÎÉÅ, Á ÚÁÔÅÍ ÏÔÐÕÓËÁÀÔ. ïÐÒÅÄÅÌÉÔØ ÚÁËÏÎ Ä×ÉÖÅÎÉÑ ÇÒÕ-
ÚÁ, ÅÓÌÉ ÓÉÌÁ, ÄÅÊÓÔ×ÕÀÝÁÑ ÎÁ ÎÅÇÏ ÓÏ ÓÔÏÒÏÎÙ ÐÒÕÖÉÎÙ, ÐÒÏÐÏÒÃÉÏÎÁÌØÎÁ
ÓÖÁÔÉÀ (ÒÁÓÔÑÖÅÎÉÀ) ÐÒÕÖÉÎÙ É ÎÁÐÒÁ×ÌÅÎÁ × ÓÔÏÒÏÎÕ ÔÏÞËÉ O (ÔÏÞËÉ,
× ËÏÔÏÒÏÊ ÎÁÈÏÄÉÌÓÑ ×ÅÒÈÎÉÊ ËÏÎÅà ÐÒÕÖÉÎÙ, ËÏÇÄÁ ÏÎÁ ÂÙÌÁ × Ó×ÏÂÏÄÎÏÍ
ÓÏÓÔÏÑÎÉÉ).
òÅÛÅÎÉÅ. åÓÌÉ ÇÒÕÚ Ä×ÉÖÅÔÓÑ ÐÒÑÍÏÌÉÎÅÊÎÏ ×ÄÏÌØ ÏÓÉ Ox, ÔÏ ÓÏÇÌÁÓÎÏ
ÚÁËÏÎÕ îØÀÔÏÎÁ
ma =
n
X
k=1
F
k
, (3)
ÇÄÅ a =
d
2
x
dt
2
¡ ÕÓËÏÒÅÎÉÅ ÇÒÕÚÁ, x = x(t) ¡ ÉÓËÏÍÙÊ ÚÁËÏÎ Ä×ÉÖÅÎÉÑ ÇÒÕÚÁ,
F
k
(k = 1, 2, . . . , n) ¡ ÐÒÏÅËÃÉÉ ÓÉÌ ÎÁ ÏÓØ Ox, ÄÅÊÓÔ×ÕÀÝÉÈ ÎÁ ÇÒÕÚ.
÷ ÎÁÛÅÍ ÓÌÕÞÁÅ ÎÁ ÇÒÕÚ ÄÅÊÓÔ×ÕÀÔ Ä×Å ÓÉÌÙ:
~
F
1
= mg~ı ¡ ×ÅÓ ÇÒÕÚÁ É
~
F
2
=
= (−cx)~ı ¡ ÓÉÌÁ, ÄÅÊÓÔ×ÕÀÝÁÑ ÓÏ ÓÔÏÒÏÎÙ ÐÒÕÖÉÎÙ, ÇÄÅ c ¡ ËÏÜÆÆÉÃÉÅÎÔ
ÖÅÓÔËÏÓÔÉ ÐÒÕÖÉÎÙ, ~ı ¡ ÅÄÉÎÉÞÎÙÊ ×ÅËÔÏÒ, ÎÁÐÒÁ×ÌÅÎÎÙÊ ×ÄÏÌØ ÏÓÉ Ox.
ðÒÏÅËÃÉÉ ÜÔÉÈ ÓÉÌ ÒÁ×ÎÙ F
1
= mg, F
2
= −cx. ðÏÌÕÞÁÅÍ ÕÒÁ×ÎÅÎÉÅ
m
d
2
x
dt
2
= −cx + mg,
ÓÏÄÅÒÖÁÝÅÅ ÎÅÉÚ×ÅÓÔÎÕÀ ÆÕÎËÃÉÀ x É ÅÅ ×ÔÏÒÕÀ ÐÒÏÉÚ×ÏÄÎÕÀ.
ðÒÏ×ÅÒËÏÊ ÍÏÖÎÏ ÕÂÅÄÉÔØÓÑ, ÞÔÏ ÕÒÁ×ÎÅÎÉÀ
d
2
x
dt
2
+ k
2
x = g, (4)
ÇÄÅ k
2
=
c
m
, ÕÄÏ×ÌÅÔ×ÏÒÑÅÔ ÆÕÎËÃÉÑ
x = c
1
cos kt + c
2
sin kt +
g
k
2
,
