Дементьев Ю.И., Самохин А.В., Жулёва Л.Д., Шевелёва В.Н. Сборник задач по высшей математике. Интегралы. Дифференциальные уравнения
Подождите немного. Документ загружается.


§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 21
ïËÏÎÞÁÔÅÌØÎÏ:
2x
2
+ 2x + 13
(x − 2)(x
2
+ 1)
2
=
1
x − 2
−
x + 2
x
2
+ 1
−
3x + 4
(x
2
+ 1)
2
.
äÌÑ ÔÏÇÏ ÞÔÏÂÙ ÐÒÏÉÎÔÅÇÒÉÒÏ×ÁÔØ ÐÒÁ×ÉÌØÎÕÀ ÄÒÏÂØ, ÅÅ ÒÁÓËÌÁÄÙ×ÁÀÔ
ÎÁ ÓÕÍÍÕ ÐÒÏÓÔÙÈ ÄÒÏÂÅÊ, Á ÚÁÔÅÍ ÉÎÔÅÇÒÉÒÕÀÔ ËÁÖÄÕÀ ÐÒÏÓÔÕÀ ÄÒÏÂØ
ÏÔÄÅÌØÎÏ É ÉÈ ÒÅÚÕÌØÔÁÔÙ ÓËÌÁÄÙ×ÁÀÔ.
ðÒÉÍÅÒ 25.
Z
2x
2
+ 2x + 13
(x − 2)(x
2
+ 1)
2
dx =
Z
dx
x − 2
−
Z
x + 2
x
2
+ 1
dx −
Z
3x + 4
(x
2
+ 1)
2
dx =
=
1
2
3 − 4x
x
2
+ 1
+
1
2
ln
(x − 2)
2
x
2
+ 1
− 4 arctg x + C.
úÄÅÓØ ÍÙ ×ÏÓÐÏÌØÚÏ×ÁÌÉÓØ ÒÁÚÌÏÖÅÎÉÅÍ ÉÚ ÐÒÉÍÅÒÁ 24.
1.5. éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ÉÒÒÁÃÉÏÎÁÌØÎÙÈ ×ÙÒÁÖÅÎÉÊ
÷ÙÛÅ ÍÙ ÎÁÕÞÉÌÉÓØ ÉÎÔÅÇÒÉÒÏ×ÁÔØ ÒÁÃÉÏÎÁÌØÎÙÅ ÆÕÎËÃÉÉ. úÄÅÓØ ÒÁÓ-
ÓÍÁÔÒÉ×ÁÅÔÓÑ ÍÅÔÏÄ ÒÁÃÉÏÎÁÌÉÚÁÃÉÉ ÄÌÑ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÉÒÒÁÃÉÏÎÁÌØÎÙÈ
×ÙÒÁÖÅÎÉÊ. á ÉÍÅÎÎÏ, ÉÝÅÔÓÑ ÐÏÄÓÔÁÎÏ×ËÁ t = t(x), ËÏÔÏÒÁÑ ÐÒÉ×ÅÌÁ ÂÙ
ÉÒÒÁÃÉÏÎÁÌØÎÏÅ ×ÙÒÁÖÅÎÉÅ Ë ÒÁÃÉÏÎÁÌØÎÏÍÕ ×ÉÄÕ. úÄÅÓØ É ÄÁÌØÛÅ ÂÕÄÅÍ
ÐÏÌÁÇÁÔØ, ÞÔÏ R(x, y, z, . . .) ¡ ÒÁÃÉÏÎÁÌØÎÁÑ ÆÕÎËÃÉÑ ÏÔ Ó×ÏÉÈ ÁÒÇÕÍÅÎÔÏ×.
I. éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ×ÙÒÁÖÅÎÉÊ ×ÉÄÁ:
Z
R
x;
m
s
ax + b
cx + p
!
dx,
ÇÄÅ m ¡ ÎÁÔÕÒÁÌØÎÏÅ ÞÉÓÌÏ, a, b, c, p ¡ ÐÏÓÔÏÑÎÎÙÅ. ðÏÌÏÖÉÍ:
t = t(x) =
m
s
ax + b
cx + p
, t
m
=
ax + b
cx + p
, x = ϕ(t) =
p · t
m
− b
a − ct
m
, dx = ϕ
0
(t) dt.
éÎÔÅÇÒÁÌ ÐÅÒÅÐÉÛÅÔÓÑ × ×ÉÄÅ:
Z
R(ϕ(t), t)ϕ
0
(t) dt.
÷ÙÞÉÓÌÉ× ÐÏÌÕÞÅÎÎÙÊ ÉÎÔÅÇÒÁÌ, ×ÅÒÎÅÍÓÑ Ë ÓÔÁÒÏÊ ÐÅÒÅÍÅÎÎÏÊ t = t(x).
ðÒÉÍÅÒ 26.
Z
1
x + 1
3
r
x + 1
x − 1
dx.
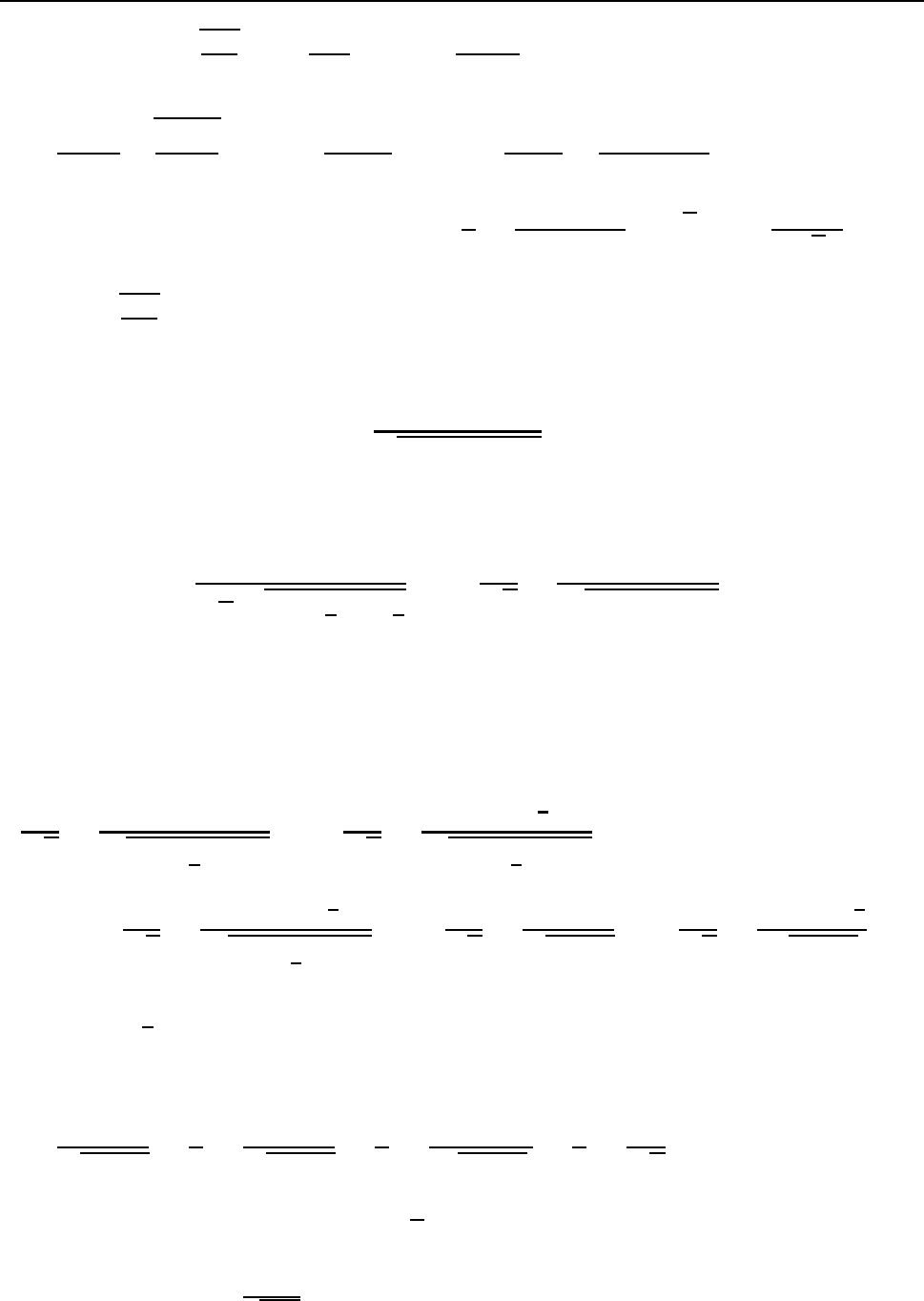
22 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
ðÏÌÁÇÁÅÍ t =
3
q
x+1
x−1
, x =
t
3
+1
t
3
−1
, dx = −
6t
2
(t
3
−1)
2
dt, ÔÏÇÄÁ
Z
1
x + 1
3
r
x + 1
x − 1
dx =
Z
−3 dt
t
3
− 1
=
Z
−
1
t − 1
+
t + 2
t
2
+ t + 1
dt =
=
1
2
ln
t
2
+ t + 1
(t − 1)
2
+
√
3 arctg
2t − 1
√
3
+ C,
ÇÄÅ t =
3
q
x+1
x−1
.
II. éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ×ÙÒÁÖÅÎÉÊ ×ÉÄÁ:
Z
Ax + B
√
ax
2
+ bx + c
dx. (3)
1) ðÕÓÔØ a > 0, ÔÏÇÄÁ ÉÎÔÅÇÒÁÌ (3) ÐÅÒÅÐÉÛÅÔÓÑ × ×ÉÄÅ
Z
Ax + B
√
a
q
x
2
+
b
a
x +
c
a
dx =
1
√
a
Z
Ax + B
p
x
2
+ px + q
dx.
ôÁË ÖÅ, ËÁË É × ÓÌÕÞÁÅ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÒÁÃÉÏÎÁÌØÎÏÊ ÆÕÎËÃÉÉ, ×ÙÄÅ-
ÌÉÍ ÐÏÌÎÙÊ Ë×ÁÄÒÁÔ × Ë×ÁÄÒÁÔÎÏÍ ÔÒÅÈÞÌÅÎÅ, ÓÔÏÑÝÅÍ × ÚÎÁÍÅÎÁÔÅÌÅ (ÓÍ.
ÐÕÎËÔ 1.4):
1
√
a
Z
Ax + B
q
x +
p
2
2
+ k
dx =
1
√
a
Z
A
x +
p
2
q
x +
p
2
2
+ k
dx+
+
1
√
a
Z
B − A ·
p
2
q
x +
p
2
2
+ k
dx =
1
√
a
Z
At
√
t
2
+ k
dt +
1
√
a
Z
B − A ·
p
2
√
t
2
+ k
dt,
ÇÄÅ t = x +
p
2
.
ðÅÒ×ÙÊ ÉÎÔÅÇÒÁÌ ×ÙÞÉÓÌÑÅÔÓÑ ÐÏÄÓÔÁÎÏ×ËÏÊ u = t
2
+ k
Z
t dt
√
t
2
+ k
=
1
2
Z
dt
2
√
t
2
+ k
=
1
2
Z
d(t
2
+ k)
√
t
2
+ k
=
1
2
Z
du
√
u
=
=
1
2
Z
u
−1/2
du = u
1/2
+ C = (t
2
+ k)
1/2
+ C.
÷ÔÏÒÏÊ ÉÎÔÅÇÒÁÌ
R
dt
√
t
2
+k
Ñ×ÌÑÅÔÓÑ ÔÁÂÌÉÞÎÙÍ.
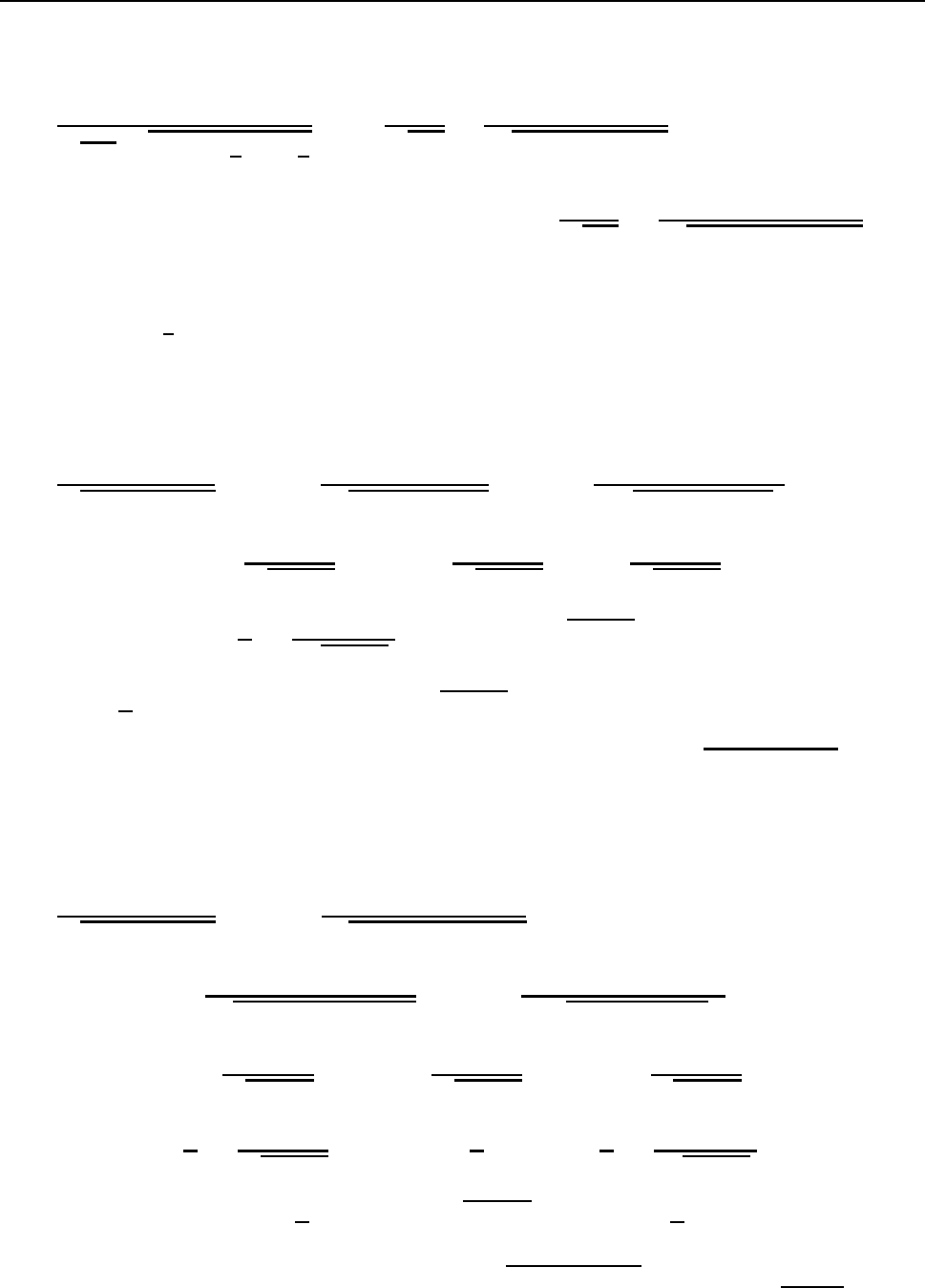
§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 23
2) ðÕÓÔØ a < 0, ÔÏÇÄÁ ÉÎÔÅÇÒÁÌ (3) ÐÅÒÅÐÉÛÅÔÓÑ × ×ÉÄÅ
Z
Ax + B
√
−a
q
−x
2
−
b
a
x −
c
a
dx =
1
√
−a
Z
Ax + B dx
p
−x
2
− px − q
=
=
1
√
−a
Z
Ax + B
p
−(x
2
+ px + q)
dx.
äÁÌØÛÅ, ×ÙÄÅÌÑÑ ÐÏÌÎÙÊ Ë×ÁÄÒÁÔ × Ë×ÁÄÒÁÔÎÏÍ ÔÒÅÈÞÌÅÎÅ É ÐÒÉÍÅÎÑÑ ÚÁ-
ÍÅÎÕ t = x +
p
2
, ÔÁË ÖÅ ËÁË É × ÐÒÅÄÙÄÕÝÅÍ ÓÌÕÞÁÅ ×ÙÞÉÓÌÑÅÍ ÐÏÌÕÞÅÎÎÙÊ
ÉÎÔÅÇÒÁÌ.
ðÒÉÍÅÒ 27.
Z
5x − 1
√
x
2
+ 2x + 2
dx =
Z
5x − 1
p
(x + 1)
2
+ 1
dx =
Z
5(x + 1 − 1) − 1
p
(x + 1)
2
+ 1
dx =
=
Z
5t − 6
√
t
2
+ 1
dt = 5
Z
t dt
√
t
2
+ 1
− 6
Z
dt
√
t
2
+ 1
=
=
5
2
Z
d(t
2
+ 1)
√
t
2
+ 1
− 6 · ln |t +
p
t
2
+ 1| + C =
=
5
2
· 2(t
2
+ 1)
1/2
− 6 ln |t +
p
t
2
+ 1| + C = 5 · (x
2
+ 2x + 2)
1/2
−
− 6 ln |x + 1 +
p
x
2
+ 2x + 3| + C.
ðÒÉÍÅÒ 28.
Z
5x + 11
√
6x − x
2
− 5
dx =
Z
5x + 11
p
−(x
2
− 6x + 5)
dx =
=
Z
5x + 11
p
−((x − 3)
2
− 4)
dx =
Z
5(x −3 + 3) + 11
p
4 − (x − 3)
2
dx =
=
Z
5t + 26
√
4 − t
2
dt = 5
Z
t
√
4 − t
2
dt + 26
Z
dt
√
4 − t
2
=
=
5
2
Z
dt
2
√
4 − t
2
+ 26 arcsin
t
2
+ C = −
5
2
Z
d(4 − t
2
)
√
4 − t
2
+
+ 26 arcsin
t
2
+ C = −5
p
4 − t
2
+ 26 arcsin
t
2
+ C =
= −5
p
6x − x
2
− 5 + 26 arcsin
x − 3
2
+ C.
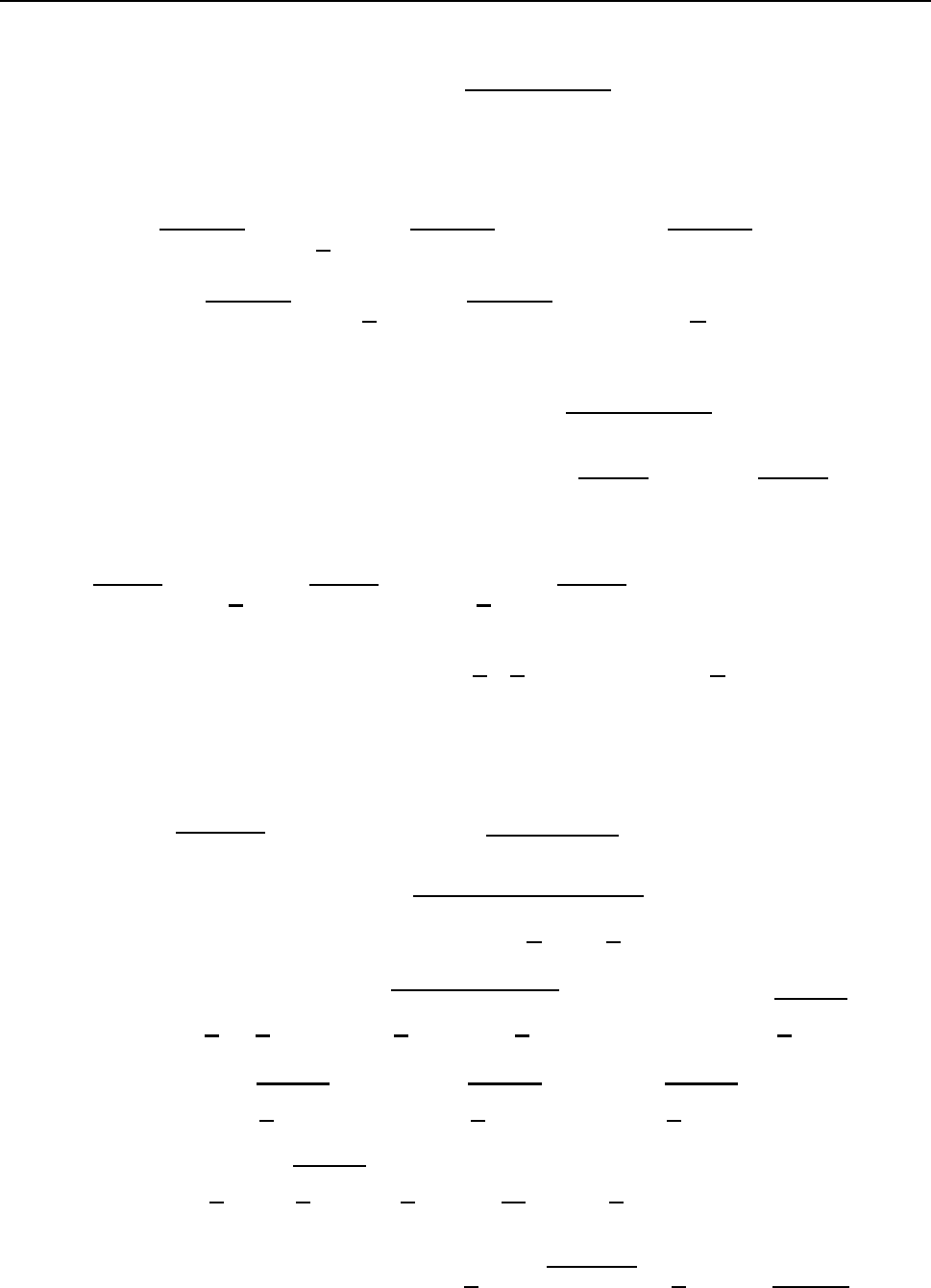
24 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
III. éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ×ÙÒÁÖÅÎÉÊ ×ÉÄÁ:
Z
(Ax + B) ·
p
ax
2
+ bx + c dx.
ðÒÉ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÉ ÜÔÉÈ ÆÕÎËÃÉÊ ÉÓÐÏÌØÚÕÀÔÓÑ ÉÎÔÅÇÒÁÌÙ
Z
p
a
2
+ x
2
dx =
1
2
(x ·
p
a
2
+ x
2
+ a
2
ln |x +
p
a
2
+ x
2
|) + C,
Z
p
a
2
− x
2
dx =
1
2
x ·
p
a
2
− x
2
+ a
2
arcsin
x
a
+ C,
ËÏÔÏÒÙÅ ×ÙÞÉÓÌÑÀÔÓÑ ÍÅÔÏÄÏÍ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÐÏ ÞÁÓÔÑÍ (ÓÍ. ÐÕÎËÔ 1.3).
äÌÑ ×ÙÞÉÓÌÅÎÉÑ ÉÎÔÅÇÒÁÌÏ×
R
(Ax + B)
√
ax
2
+ bx + c dx × Ë×ÁÄÒÁÔÎÏÍ
ÔÒÅÈÞÌÅÎÅ ×ÙÄÅÌÑÅÔÓÑ ÐÏÌÎÙÊ Ë×ÁÄÒÁÔ, Á ÚÁÔÅÍ, ÁÎÁÌÏÇÉÞÎÏ ÓÌÕÞÁÀ II, ×ÓÅ
Ó×ÏÄÉÔÓÑ Ë ×ÙÞÉÓÌÅÎÉÀ ÉÎÔÅÇÒÁÌÏ× ×ÉÄÁ
R
t
√
k ± t
2
dt É
R
√
k ± t
2
dt. ðÅÒ-
×ÙÊ ÉÚ ÐÏÌÕÞÅÎÎÙÈ ÉÎÔÅÇÒÁÌÏ× ×ÙÞÉÓÌÑÅÍ:
Z
t
p
k ± t
2
dt =
1
2
Z
p
k ± t
2
dt
2
= ±
1
2
Z
p
k ± t
2
d(k ± t
2
) =
= ±
1
2
·
2
3
(k ± t
2
)
3/2
= ±
1
3
(k ± t
2
)
3/2
+ C.
úÎÁÞÅÎÉÅ ×ÔÏÒÏÇÏ ÉÎÔÅÇÒÁÌÁ ÓÍ. ×ÙÛÅ.
ðÒÉÍÅÒ 29.
Z
(2x − 1)
p
3x − x
2
dx =
Z
(2x − 1)
p
−(x
2
− 3x) dx =
=
Z
(2x −1)
s
−
x −
3
2
2
−
9
4
dx =
=
Z
2
x −
3
2
+
3
2
− 1
s
9
4
−
x −
3
2
2
dx =
Z
(2t + 2)
r
9
4
− t
2
dt =
= 2
Z
t
r
9
4
− t
2
dt + 2
Z
r
9
4
− t
2
dt =
Z
r
9
4
− t
2
dt
2
+
+ 2 ·
1
2
t
r
9
4
− t
2
+
9
4
arcsin
2t
3
!
= −
2
3
(3x −x
2
)
3/2
+
+
x −
3
2
·
p
3x − x
2
+
9
4
arcsin
2x − 3
3
+ C.

§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 25
IV. éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ÄÉÆÆÅÒÅÎÃÉÁÌØÎÙÈ ÂÉÎÏÍÏ× ×ÉÄÁ:
Z
x
m
(a + bx
n
)
p
dx,
ÇÄÅ p =
α
β
; α, β ¡ ÃÅÌÙÅ ÞÉÓÌÁ; m, n ¡ ÐÒÏÉÚ×ÏÌØÎÙÅ ÞÉÓÌÁ.
äÁÎÎÙÊ ÉÎÔÅÇÒÁÌ ÉÎÔÅÇÒÉÒÕÅÔÓÑ ÌÉÛØ × ÓÌÅÄÕÀÝÉÈ ÔÒÅÈ ÓÌÕÞÁÑÈ:
1) ÅÓÌÉ p ÃÅÌÏÅ ÞÉÓÌÏ, ÔÏ ÉÓÐÏÌØÚÕÅÔÓÑ ÐÏÄÓÔÁÎÏ×ËÁ
x = t
N
, ÇÄÅ N ¡ ÏÂÝÉÊ ÚÎÁÍÅÎÁÔÅÌØ ÄÒÏÂÅÊ m É n;
2) ÅÓÌÉ
m+1
n
ÃÅÌÏÅ ÞÉÓÌÏ, ÔÏ ÉÓÐÏÌØÚÕÅÔÓÑ ÐÏÄÓÔÁÎÏ×ËÁ
a + bx
n
= t
β
;
3) ÅÓÌÉ
m+1
n
+ p ÃÅÌÏÅ ÞÉÓÌÏ, ÔÏ ÉÓÐÏÌØÚÕÅÔÓÑ ÐÏÄÓÔÁÎÏ×ËÁ
a + bx
n
= x
n
t
β
.
ðÒÉÍÅÒ 30.
Z
x
3
√
x
2
− 1
dx,
ÇÄÅ m = 3, n = 2. þÉÓÌÏ
m+1
n
=
3+1
2
= 2 ¡ ÃÅÌÏÅ, ÐÏÜÔÏÍÕ ÉÓÐÏÌØÚÕÅÍ
ÐÏÄÓÔÁÎÏ×ËÕ (1): x
2
− 1 = t
2
, x =
√
t
2
+ 1, dx =
t
√
1+t
2
dt, ÏÔÓÀÄÁ
Z
x
3
√
x
2
− 1
dx =
Z
(1 + t
2
)
3/2
t
·
t
(t
2
+ 1)
1/2
dt =
Z
(1 + t
2
) dt =
= t +
t
3
3
+ C = (x
2
− 1)
1/2
+
(x
2
− 1)
3/2
3
+ C.
ðÒÉÍÅÒ 31.
Z
dx
4
√
1 + x
4
=
Z
x
0
(1 + x
4
)
−1/4
dx,
ÚÄÅÓØ m = 0, n = 4, p = −
1
4
. ðÒÏ×ÅÒÉÍ ÕÓÌÏ×ÉÅ:
m+1
n
+ p ¡ ÃÅÌÏÅ ÞÉÓÌÏ ÉÌÉ
ÎÏÌØ.
m+1
n
+p =
0+1
4
−
1
4
= 0, ÐÏÜÔÏÍÕ ÉÓÐÏÌØÚÕÅÍ ÐÏÄÓÔÁÎÏ×ËÕ (2); ÚÄÅÓØ β = 4:
1 + x
4
= x
4
· t
4
, t =
4
q
1
x
4
+ 1 =
4
√
1+x
4
x
, x = (t
4
− 1)
−1/4
, dx = −t
3
(t
4
−1)
−5/4
dt,
ÔÁË ÞÔÏ
4
√
1 + x
4
= tx = t · (t
4
− 1)
−1/4
,
Z
dx
4
√
1 + x
4
= −
Z
t
2
dt
t
4
− 1
=
1
4
Z
1
t + 1
−
1
t − 1
dt −
1
2
Z
dt
t
2
+ 1
=
=
1
4
ln
t + 1
t − 1
−
1
2
arctg t + C,
ÇÄÅ t =
4
√
1+x
4
x
.
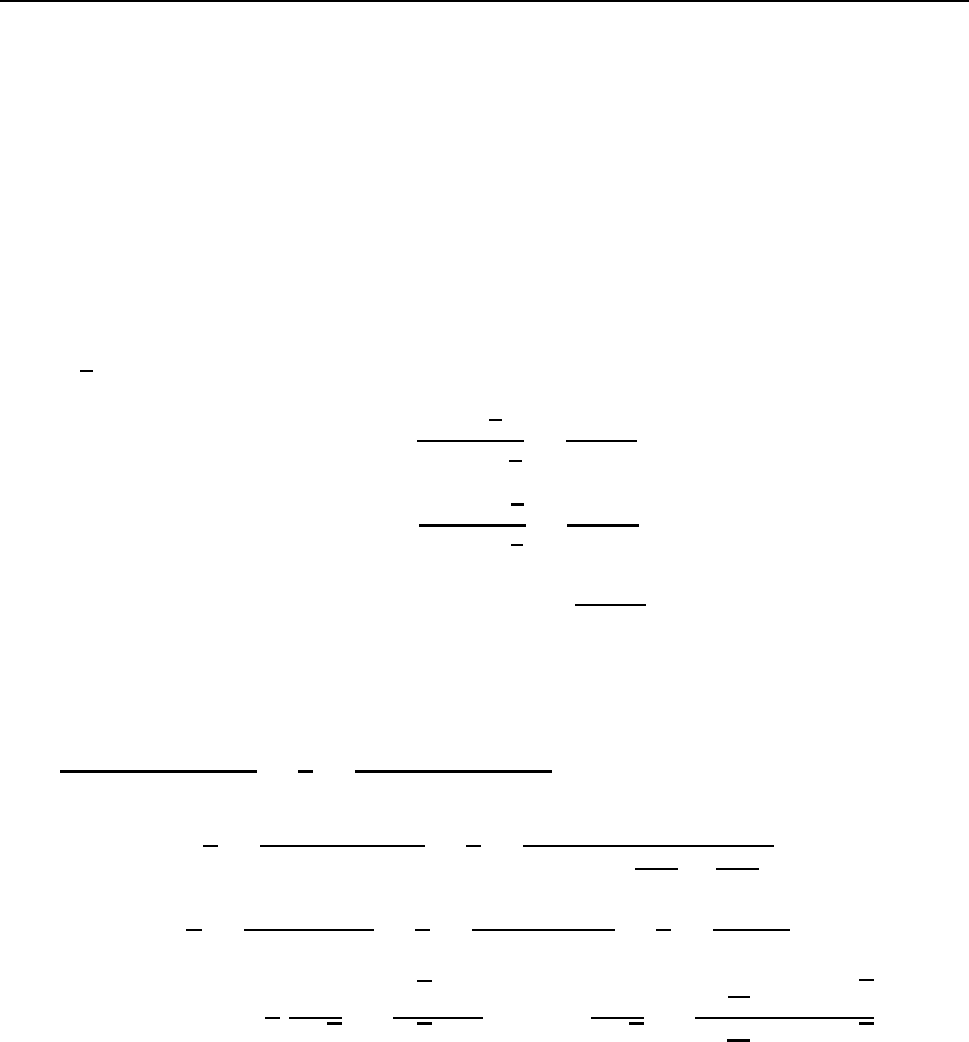
26 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
1.6. éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ×ÙÒÁÖÅÎÉÊ, ÓÏÄÅÒÖÁÝÉÈ ÔÒÉÇÏÎÏÍÅÔÒÉÞÅ-
ÓËÉÅ ÆÕÎËÃÉÉ
I. éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ×ÙÒÁÖÅÎÉÊ ×ÉÄÁ
Z
R(sin x, cos x) dx,
ÇÄÅ R ¡ ÒÁÃÉÏÎÁÌØÎÁÑ ÆÕÎËÃÉÑ.
÷ ÜÔÏÍ ÓÌÕÞÁÅ ÓÕÝÅÓÔ×ÕÅÔ ÕÎÉ×ÅÒÓÁÌØÎÙÊ ÐÒÉÅÍ ÒÁÃÉÏÎÁÌÉÚÁÃÉÉ ×ÙÒÁ-
ÖÅÎÉÊ, ÓÔÏÑÝÉÈ ÐÏÄ ÚÎÁËÏÍ ÉÎÔÅÇÒÁÌÁ. á ÉÍÅÎÎÏ, ÉÓÐÏÌØÚÕÑ ÐÏÄÓÔÁÎÏ×ËÕ
t = tg
x
2
(−π < x < π) É ÔÒÉÇÏÎÏÍÅÔÒÉÞÅÓËÉÅ ÆÏÒÍÕÌÙ:
sin x =
2 tg
x
2
1 + tg
2
x
2
=
2t
1 + t
2
,
cos x =
1 − tg
2
x
2
1 + tg
2
x
2
=
1 − t
2
1 + t
2
,
x = 2 arctg t, dx =
2 dt
1 + t
2
,
ÐÏÌÕÞÉÍ ÐÏÄ ÉÎÔÅÇÒÁÌÏÍ ÒÁÃÉÏÎÁÌØÎÕÀ ÆÕÎËÃÉÀ.
ðÒÉÍÅÒ 32.
Z
dx
cos 3x + 2 sin 3x
=
1
3
Z
d3x
cos 3x + 2 sin 3x
=
=
1
3
Z
dz
cos z + 2 sin z
=
1
3
Z
2 dt
(1 + t
2
)
1−t
2
1+t
2
+
4t
1+t
2
=
=
2
3
Z
dt
1 − t
2
+ 4t
=
2
3
Z
dt
5 − (t − 2)
2
=
2
3
Z
du
5 − u
2
=
=
2
3
1
2
√
5
ln
√
5 + u
√
5 − u
+ C =
1
3
√
5
ln
tg
3x
2
− 2 +
√
5
tg
3x
2
− 2 −
√
5
+ C.
ðÏÄÓÔÁÎÏ×ËÁ, ÕÐÏÍÑÎÕÔÁÑ ×ÙÛÅ, ÐÒÉ×ÏÄÉÔ ÞÁÓÔÏ Ë ÓÌÏÖÎÙÍ ÐÒÅÏÂÒÁÚÏ-
×ÁÎÉÑÍ, ÐÏÜÔÏÍÕ × ÎÉÖÅÐÒÉ×ÅÄÅÎÎÙÈ ÞÁÓÔÎÙÈ ÓÌÕÞÁÑÈ ÐÒÅÄÐÏÞÔÉÔÅÌØÎÙ
ÓÌÅÄÕÀÝÉÅ, ÂÏÌÅÅ ÕÄÏÂÎÙÅ ÐÒÉÅÍÙ:
Á) ÐÕÓÔØ R(u, v) = −R(−u, v), ÔÏÇÄÁ ÒÁÃÉÏÎÁÌÉÚÁÃÉÑ ÄÏÓÔÉÇÁÅÔÓÑ ÐÏÄÓÔÁ-
ÎÏ×ËÏÊ t = cos x;
Â) ÐÕÓÔØ R(u, v) = −R(u, −v), ÔÏÇÄÁ ÒÁÃÉÏÎÁÌÉÚÁÃÉÑ ÄÏÓÔÉÇÁÅÔÓÑ ÐÏÄÓÔÁ-
ÎÏ×ËÏÊ t = sin x;
×) ÐÕÓÔØ R(u, v) = R(−u, −v), ÔÏÇÄÁ ÒÁÃÉÏÎÁÌÉÚÁÃÉÑ ÄÏÓÔÉÇÁÅÔÓÑ ÐÏÄÓÔÁ-
ÎÏ×ËÏÊ t = tg x.

§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 27
ðÒÉÍÅÒ 33.
Z
sin x
4 + cos
2
x
dx,
R(sin x, cos x) =
sin x
4 + cos
2
x
,
R(−sin x, cos x) = −
sin x
4 + cos
2
x
,
R(sin x, cos x) = −R(−sin x, cos x),
ÐÏÜÔÏÍÕ ÉÓÐÏÌØÚÕÅÍ ÐÏÄÓÔÁÎÏ×ËÕ t = cos x:
Z
sin x
4 + cos
2
x
dx = −
Z
d cos x
4 + cos
2
x
= −
Z
dt
4 + t
2
= −
1
2
arctg
cos x
2
+ C.
ðÒÉÍÅÒ 34.
Z
dx
sin
2
x − 5 sin x cos x
,
R(sin x, cos x) =
1
sin
2
x − 5 sin x cos x
,
R(−sin x, −cos x) =
1
sin
2
x − 5 sin x cos x
,
R(sin x, cos x) = R(−sin x, −cos x),
ÉÓÐÏÌØÚÕÅÍ ÐÏÄÓÔÁÎÏ×ËÕ t = tg x:
Z
dx
sin
2
x − 5 sin x cos x
=
Z
dx
cos
2
x
sin
2
x
cos
2
x
−
5 sin x cos x
cos
2
x
=
=
Z
d tg x
tg
2
x − 5 tg x
=
Z
dt
t
2
− 5t
=
Z
dt
t −
5
2
2
−
5
2
2
=
= −
1
5
ln
5
2
+ t −
5
2
5
2
− t +
5
2
= −
1
5
ln
t
t − 5
+ C =
=
1
5
ln
1 −
5
t
+ C =
1
5
ln |1 − 5 ctg x| + C.
II. éÎÔÅÇÒÁÌÙ ×ÉÄÁ
R
sin
m
x cos
n
x dx.
ðÒÉ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÉ ÜÔÉÈ ×ÙÒÁÖÅÎÉÊ ÏËÁÚÙ×ÁÀÔÓÑ ÐÏÌÅÚÎÙÍÉ ÓÌÅÄÕÀ-
ÝÉÅ ÔÒÉÇÏÎÏÍÅÔÒÉÞÅÓËÉÅ ÆÏÒÍÕÌÙ
sin x cos x =
sin 2x
2
, sin
2
x =
1 − cos 2x
2
, cos
2
x =
1 + cos 2x
2
.
1. òÁÓÓÍÏÔÒÉÍ ÉÎÔÅÇÒÁÌÙ ×ÉÄÁ:
R
sin
m
x dx,
R
cos
m
x dx, ÐÏÌÁÇÁÅÍ, ÞÔÏ

28 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
Á) m > 0, ÞÅÔÎÏÅ, m = 2k.
Z
sin
m
x dx =
Z
(sin
2
x)
k
dx =
Z
(1 − cos 2x)
k
2
k
dx =
1
2
k+1
Z
(1 − cos 2x)
k
d2x.
Â) m > 0, ÎÅÞÅÔÎÏÅ, m = 2k + 1.
Z
sin
m
x dx =
Z
sin
2k
x · sin x dx =
= −
Z
(sin
2
x)
k
d cos x = −
Z
(1 − cos
2
x)
k
d cos x = −
Z
(1 − t
2
)
k
dt,
ÇÄÅ t = cos x.
÷ÏÚ×ÅÄÑ ×ÙÒÁÖÅÎÉÑ, ÓÔÏÑÝÉÅ ÐÏÄ ÉÎÔÅÇÒÁÌÁÍÉ ÐÏ ÂÉÎÏÍÕ îØÀÔÏÎÁ × ÓÏ-
ÏÔ×ÅÔÓÔ×ÕÀÝÕÀ ÓÔÅÐÅÎØ, ÐÏÌÕÞÁÅÍ ÒÑÄ ÉÎÔÅÇÒÁÌÏ× ÔÉÐÁ (Á) É (Â), ÎÏ Ó ÎÉÚ-
ÛÉÍÉ ÓÔÅÐÅÎÑÍÉ, ÉÈ ÄÁÌØÛÅ ÕÐÒÏÝÁÅÍ ÔÅÍ ÖÅ ÏÂÒÁÚÏÍ.
óÌÕÞÁÊ
R
cos
m
x dx ÄÅÌÁÅÔÓÑ ÁÎÁÌÏÇÉÞÎÏ.
ðÒÉÍÅÒ 35.
Z
cos
4
x dx =
Z
(cos
2
x)
2
dx =
Z
(1 + cos 2x)
2
8
d2x =
=
1
8
Z
(1 + 2 cos z + cos
2
z) dz =
z
8
+
sin z
4
+
+
1
8
Z
1 + cos 2z
2
dz =
3
8
x +
sin 2x
4
+
sin 4x
32
+ C.
ðÒÉÍÅÒ 36.
Z
cos
3
x dx =
Z
cos
2
x d sin x =
Z
(1 − sin
2
x) d sin x =
=
Z
(1 − t
2
) dt = t −
t
3
3
+ C = sin x −
sin
3
x
3
+ C.
×) m = −1
Z
dx
sin x
,
Z
dx
cos x
.
Z
dx
sin x
=
Z
dx
2 sin
x
2
cos
x
2
=
Z
d
x
2
cos
2
x
2
sin
x
2
cos
x
2
=
Z
d tg
x
2
tg
x
2
= ln
tg
x
2
+ C,
Z
dx
cos x
=
Z
d
x +
π
2
sin
x +
π
2
= ln
tg
x
2
+
π
4
+ C.

§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 29
Ç) m < 0, |m| = 2k.
Z
cos
m
x dx =
Z
dx
cos
2k
x
=
Z
1
cos
2
x
k−1
dx
cos
2
x
=
=
Z
sin
2
x + cos
2
x
cos
2
x
k−1
d tg x =
Z
(1 + tg
2
x)
k−1
d tg x =
=
Z
(1 + t
2
)
k−1
dt, t = tg x,
ÁÎÁÌÏÇÉÞÎÏ
Z
sin
m
x dx =
Z
dx
sin
2k
x
= −
Z
(1 + ctg
2
x)
k−1
d ctg x.
ðÒÉÍÅÒ 37.
Z
dx
cos
4
x
=
Z
1
cos
2
x
dx
cos
2
x
=
Z
sin
2
x + cos
2
x
cos
2
x
d tg x =
Z
(tg
2
x + 1) d tg x =
=
Z
(t
2
+ 1) dt =
t
3
3
+ t + C =
tg
3
x
3
+ tg x + C.
Ä) m < 0, |m| = 2k + 1.
Z
cos
m
x dx =
Z
dx
cos
2k+1
x
=
Z
cos x
cos
2k+2
x
dx =
=
Z
d sin x
(1 − sin
2
x)
k+1
=
Z
dt
(1 − t
2
)
k+1
ÄÁÌÅÅ ÓÍ. ÐÕÎËÔ 1.4. óÌÕÞÁÊ
R
dx
sin
2k+1
x
ÄÅÌÁÅÔÓÑ ÁÎÁÌÏÇÉÞÎÏ.
ðÒÉÍÅÒ 38.
Z
dx
cos
3
x
=
Z
cos x dx
cos
4
x
=
Z
d sin x
(cos
2
x)
2
=
Z
d sin x
(1 − sin
2
x)
2
=
Z
dt
(1 − t
2
)
2
;
(ÄÁÌÅÅ ÓÍ. ÐÕÎËÔ 1.4).
÷ ÓÌÕÞÁÅ Ä) ÄÌÑ ÐÏÎÉÖÅÎÉÑ ÓÔÅÐÅÎÉ ÕÄÏÂÎÏ ÐÒÉÍÅÎÑÔØ ÆÏÒÍÕÌÕ sin
2
x +
+ cos
2
x = 1.
Z
dx
cos
3
x
=
Z
sin
2
x + cos
2
x
cos
3
x
dx =
=
Z
sin
2
x
cos
3
x
+
1
cos x
dx = ln
tg
x
2
+
π
4
−
Z
sin x
cos
3
x
d cos x.

30 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
éÎÔÅÇÒÉÒÕÑ ÐÏÓÌÅÄÎÉÊ ÉÎÔÅÇÒÁÌ ÐÏ ÞÁÓÔÑÍ, ÐÏÌÕÞÉÍ:
−
Z
sin x
cos
3
x
d cos x =
1
2
Z
sin x d cos
−2
x =
=
1
2
sin x
cos
2
x
−
Z
d sin x
cos
2
x
=
1
2
sin x
cos
2
x
−
Z
dx
cos x
=
=
1
2
sin x
cos
2
x
−
1
2
ln
tg
x
2
+
π
4
.
ïËÏÎÞÁÔÅÌØÎÏ ÐÏÌÕÞÉÍ:
Z
dx
cos
3
x
=
1
2
ln
tg
x
2
+
π
4
+
1
2
sin x
cos
2
x
.
2) òÁÓÓÍÏÔÒÉÍ ÉÎÔÅÇÒÁÌÙ ×ÉÄÁ
Z
sin
m
x cos
n
x dx, m > 0, n > 0.
Å) ÏÄÉÎ ÉÚ ÐÏËÁÚÁÔÅÌÅÊ m ÉÌÉ n ÎÅÞÅÔÎÙÊ, ÂÅÚ ÉÚÍÅÎÅÎÉÑ ÏÂÝÎÏÓÔÉ ÐÏ-
ÌÁÇÁÅÍ n = 2k + 1.
Z
sin
m
cos
n
x dx =
Z
sin
m
x cos
2k+1
x dx =
Z
sin
m
x(cos
2
x)
k
d sin x =
=
Z
sin
m
x(1 − sin
2
x)
k
d sin x =
Z
t
m
(1 − t
2
)
k
dt,
ÇÄÅ t = sin x É ÄÁÌÅÅ ÐÏ ÂÉÎÏÍÕ îØÀÔÏÎÁ.
ðÒÉÍÅÒ 39.
Z
sin
2
x cos
3
x dx =
Z
sin
2
x cos
2
x d sin x =
=
Z
sin
2
x(1 − sin
2
x) d sin x =
Z
t
2
(1 − t
2
) dt =
=
Z
(t
2
− t
4
) dt =
t
3
3
−
t
5
5
+ C =
sin
3
x
3
−
sin
5
x
5
+ C.
Ö) m É n ÞÅÔÎÙÅ, ÔÏ ÅÓÔØ m = 2k, n = 2l,
Z
sin
m
x cos
n
x dx =
Z
sin
2k
x cos
2l
x dx =
Z
sin
2k
x(1 − sin
2
x)
l
dx,
ÄÁÌÅÅ, ÉÓÐÏÌØÚÕÑ ÂÉÎÏÍ îØÀÔÏÎÁ, Ó×ÏÄÉÍ Ë ÓÌÕÞÁÀ Á).
ðÒÉÍÅÒ 40.
Z
sin
2
x cos
2
x dx =
Z
sin
2
(1 − sin
2
x) dx =
Z
sin
2
x dx −
Z
sin
4
x dx.
