Дементьев Ю.И., Самохин А.В., Жулёва Л.Д., Шевелёва В.Н. Сборник задач по высшей математике. Интегралы. Дифференциальные уравнения
Подождите немного. Документ загружается.

§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 11
ðÒÉÍÅÒ 11.
Z
e
2x
e
2x
+ 1
dx =
1
2
Z
e
2x
e
2x
+ 1
d2x =
1
2
Z
de
2x
e
2x
+ 1
=
1
2
Z
d(e
2x
+ 1)
e
2x
+ 1
=
=
1
2
Z
dt
t
=
1
2
ln |t| + C =
1
2
ln(e
2x
+ 1) + C.
ðÒÉÍÅÒ 12.
Z
x dx
5x
2
− 3
=
1
2
Z
dx
2
5x
2
− 3
=
1
2 · 5
Z
d(5x
2
− 3)
5x
2
− 3
=
=
1
10
Z
dt
t
=
1
10
ln |t| + C =
1
10
ln |5x
2
− 3| + C.
II. ðÒÉÍÅÎÑÑ ×ÔÏÒÕÀ ÆÏÒÍÕ ÐÏÄÓÔÁÎÏ×ËÉ, ÐÏÌØÚÕÀÔÓÑ ÐÒÁ×ÉÌÏÍ 4. ÷ ÐÏ-
ÄÙÎÔÅÇÒÁÌØÎÏÅ ×ÙÒÁÖÅÎÉÅ ÎÅÐÏÓÒÅÄÓÔ×ÅÎÎÏ ÐÏÄÓÔÁ×ÌÑÀÔ ×ÍÅÓÔÏ x ÆÕÎËÃÉÀ
x = ω(t), Á ÉÍÅÎÎÏ:
Z
f(x) dx =
Z
f(ω(t)) dω(t) =
Z
f(ω(t))ω
0
(t) dt =
Z
g(t) dt,
ÇÄÅ g(t) ¡ ÂÏÌÅÅ ÕÄÏÂÎÁÑ ÄÌÑ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÆÕÎËÃÉÑ, ÞÅÍ f(x). ðÒÉ ÜÔÏÍ
ÎÁ ÆÕÎËÃÉÀ ω(t) ÎÁËÌÁÄÙ×ÁÀÔÓÑ ÕÓÌÏ×ÉÑ ÓÔÒÏÇÏÊ ÍÏÎÏÔÏÎÎÏÓÔÉ, ÞÔÏ ÏÂÅÓ-
ÐÅÞÉ×ÁÅÔ ÓÕÝÅÓÔ×Ï×ÁÎÉÅ ÏÂÒÁÔÎÏÊ ÆÕÎËÃÉÉ t = v(x) É ÐÒÅÄÓÔÁ×ÌÅÎÉÅ:
Z
f(x) dx =
Z
g(t) dt = G(t) + C = G(v(x)) + C.
ðÒÉÍÅÒ 13.
Z
dx
√
x (4 +
3
√
x)
.
ðÒÉÍÅÎÑÑ ÐÏÄÓÔÁÎÏ×ËÕ x = t
6
, ÐÏÌÕÞÉÍ
√
x = t
3
,
3
√
x = t
2
, dx = dt
6
= 6t
5
dt
É
Z
6t
5
dt
t
3
(4 + t
2
)
= 6
Z
t
2
4 + t
2
dt = 6
Z
t
2
+ 4 − 4
t
2
+ 4
dt =
= 6
Z
1 −
4
t
2
+ 4
dt = 6
Z
dt − 24
Z
dt
t
2
+ 4
=
= 6t − 12 arctg
t
2
+ C = 6
6
√
x + 12 arctg
6
√
x
2
+ C.
ðÒÉÍÅÒ 14.
Z
p
9 − x
2
dx.
12 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
ðÒÉÍÅÎÑÑ ÐÏÄÓÔÁÎÏ×ËÕ x = 3 sin t, −3 6 x 6 3, −
π
2
6 t 6
π
2
, t = arcsin
x
3
,
dx = d(3 sin t) = 3 cos t dt, ÐÏÌÕÞÉÍ
Z
p
9 − 9 sin
2
t 3 cos t dt =
Z
√
9 cos
2
t 3 cos t dt = 9
Z
cos
2
t dt =
= 9
Z
1 + cos 2t
2
dt =
9
2
Z
dt +
Z
cos 2t dt
=
9
2
t +
9
4
sin 2t + C =
=
9
2
arcsin
x
3
+
9
4
sin
2 arcsin
x
3
+ C.
ðÒÅÏÂÒÁÚÕÅÍ ÏÔÄÅÌØÎÏ ×ÙÒÁÖÅÎÉÅ sin
2
arcsin
x
3
, ÄÌÑ ÜÔÏÇÏ ×ÏÓÐÏÌØÚÕÅÍÓÑ
ÆÏÒÍÕÌÏÊ:
sin 2t = 2 sin t cos t = 2 sin t ·
p
1 − sin
2
t, −
π
2
6 t 6
π
2
,
ÐÏÜÔÏÍÕ
sin
2 arcsin
x
3
= 2 sin
arcsin
x
3
·
r
1 − sin
2
arcsin
x
3
=
= 2 ·
x
3
·
r
1 −
x
2
9
=
2
9
x ·
p
9 − x
2
.
ïÔÓÀÄÁ ÏËÏÎÞÁÔÅÌØÎÏ ÐÏÌÕÞÉÍ:
Z
p
9 − x
2
dx =
9
2
arcsin
x
3
+
1
2
x ·
p
9 − x
2
+ C.
1.3. éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ÐÏ ÞÁÓÔÑÍ
ðÕÓÔØ ÆÕÎËÃÉÉ u(x), v(x) ÉÍÅÀÔ ÎÅÐÒÅÒÙ×ÎÙÅ ÐÒÏÉÚ×ÏÄÎÙÅ u
0
(x), v
0
(x)
ÎÁ ÐÒÏÍÅÖÕÔËÅ (a, b), ÔÏÇÄÁ ÓÐÒÁ×ÅÄÌÉ×Ï ÒÁ×ÅÎÓÔ×Ï:
Z
u(x)v
0
(x) dx = u(x)v(x) −
Z
v(x)u
0
(x) dx (1)
ÉÌÉ
Z
u dv = uv −
Z
v du.
îÅÏÂÈÏÄÉÍÏ ÚÁÍÅÔÉÔØ, ÞÔÏ ÐÒÉÍÅÎÅÎÉÅ ÍÅÔÏÄÁ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÐÏ ÞÁÓÔÑÍ
ÐÒÉ×ÏÄÉÔ Ë ÞÁÓÔÉÞÎÏÍÕ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÀ, ÔÁË ËÁË É ÐÒÁ×ÁÑ ÞÁÓÔØ ÆÏÒÍÕÌÙ
(1) ÓÏÄÅÒÖÉÔ ÉÎÔÅÇÒÁÌ. ïÄÎÁËÏ ÐÒÉ ÐÒÁ×ÉÌØÎÏÍ ÐÒÉÍÅÎÅÎÉÉ ÍÅÔÏÄÁ ÉÎÔÅ-
ÇÒÁÌ ÉÚ ÐÒÁ×ÏÊ ÞÁÓÔÉ (1) ÂÕÄÅÔ ÔÁÂÌÉÞÎÙÍ ÉÌÉ ÌÅÇËÏ Ó×ÏÄÑÝÉÍÓÑ Ë ÔÁ-
ÂÌÉÞÎÏÍÕ. ðÒÉ ×ÙÞÉÓÌÅÎÉÉ ÎÅËÏÔÏÒÙÈ ÉÎÔÅÇÒÁÌÏ× ÍÅÔÏÄ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ
ÐÏ ÞÁÓÔÑÍ ÍÏÖÅÔ ÐÒÉÍÅÎÑÔØÓÑ ÎÅÓËÏÌØËÏ ÒÁÚ. ðÒÁ×ÉÌÏ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÐÏ

§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 13
ÞÁÓÔÑÍ ÉÍÅÅÔ ÂÏÌÅÅ ÏÇÒÁÎÉÞÅÎÎÕÀ ÏÂÌÁÓÔØ ÐÒÉÍÅÎÅÎÉÑ, ÞÅÍ ÚÁÍÅÎÁ ÐÅÒÅ-
ÍÅÎÎÏÊ. îÏ ÅÓÔØ ÃÅÌÙÅ ËÌÁÓÓÙ ÉÎÔÅÇÒÁÌÏ×, ÎÁÐÒÉÍÅÒ:
Z
x
k
ln
m
x dx,
Z
x
k
sin ax dx,
Z
x
k
cos ax dx,
Z
x
k
e
ax
dx,
Z
x
k
arcsin ax dx,
Z
x
k
arccos ax dx,
Z
x
k
arctg ax dx
É ÄÒÕÇÉÅ, ËÏÔÏÒÙÅ ×ÙÞÉÓÌÑÀÔÓÑ ÉÍÅÎÎÏ Ó ÐÏÍÏÝØÀ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÐÏ ÞÁ-
ÓÔÑÍ.
I. ðÒÉ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÉ ÆÕÎËÃÉÊ ×ÉÄÁ P
m
(x) sin ax, P
m
(x) cos ax, P
m
(x)e
ax
,
ÇÄÅ P
m
(x) ÐÒÏÉÚ×ÏÌØÎÙÊ ÍÎÏÇÏÞÌÅÎ ÓÔÅÐÅÎÉ m, × ËÁÞÅÓÔ×Å ÆÕÎËÃÉÉ u(x) ÉÚ
ÆÏÒÍÕÌÙ (1) ÂÅÒÅÔÓÑ ÍÎÏÇÏÞÌÅÎ P
m
(x), Á × ËÁÞÅÓÔ×Å v
0
(x) ÄÒÕÇÏÊ ÓÏÍÎÏÖÉ-
ÔÅÌØ.
ðÒÉÍÅÒ 15.
R
x · sin 3x dx. ðÕÓÔØ u(x) = x, v
0
(x) = sin 3x, ÔÏÇÄÁ
dv = sin 3x dx =
sin 3x
3
d3x = −
1
3
d cos 3x.
Z
x · sin 3x dx = −
1
3
Z
x d cos 3x = −
1
3
x · cos 3x −
Z
cos 3x dx
=
= −
1
3
x cos 3x +
1
3
Z
cos 3x dx = −
1
3
x cos 3x +
1
9
Z
cos 3x d3x =
= −
1
3
x cos 3x +
1
9
sin 3x + C.
ðÒÉÍÅÒ 16.
R
xe
−4x
dx. ðÕÓÔØ u(x) = x, v
0
(x) = e
−4x
, ÔÏÇÄÁ
v
0
(x) dx = dv(x) = e
−4x
dx = −
e
−4x
4
d(−4x) = −
1
4
de
−4x
.
Z
xe
−4x
dx = −
1
4
Z
x de
−4x
= −
1
4
x · e
−4x
−
Z
e
−4x
dx
=
= −
1
4
xe
−4x
+
1
4
Z
e
−4x
dx = −
1
4
xe
−4x
−
1
16
Z
e
−4x
d(−4x) =
= −
1
4
xe
−4x
−
1
16
e
−4x
+ C.
ëÁË ÂÙÌÏ ÓËÁÚÁÎÏ ×ÙÛÅ, ÐÒÉ ×ÙÞÉÓÌÅÎÉÉ ÉÎÔÅÇÒÁÌÏ× ÆÏÒÍÕÌÁ ÉÎÔÅÇÒÉ-
ÒÏ×ÁÎÉÑ ÐÏ ÞÁÓÔÑÍ ÍÏÖÅÔ ÐÒÉÍÅÎÑÔØÓÑ ÎÅÓËÏÌØËÏ ÒÁÚ.
14 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
ðÒÉÍÅÒ 17.
R
x
2
· cos 2x dx. ðÕÓÔØ u(x) = x
2
, v
0
(x) = cos 2x, ÔÏÇÄÁ
v
0
(x) dx = dv(x) = cos 2x dx =
1
2
cos 2x d2x =
1
2
d sin 2x.
Z
x
2
cos 2x dx =
1
2
Z
x
2
d sin 2x =
1
2
x
2
sin 2x −
Z
sin 2x dx
2
. (2)
ôÁË ËÁË dx
2
= 2x dx, ÔÏ × ÐÏÓÌÅÄÎÅÍ ÉÎÔÅÇÒÁÌÅ ÐÏÌÕÞÉÍ
Z
sin 2x dx
2
=
Z
(sin 2x) · 2x dx.
ðÏÌÁÇÁÑ u(x) = 2x, v
0
(x) = sin 2x; v
0
(x) dx = sin 2x dx =
1
2
sin 2x d2x =
= −
1
2
d cos 2x, ÉÍÅÅÍ
Z
(sin 2x) · 2x dx =
Z
2x ·
−
1
2
d cos 2x = −
Z
x d cos 2x =
= −
x cos 2x −
Z
cos 2x dx
= −x cos 2x +
1
2
Z
cos 2x d2x =
= −x cos 2x +
1
2
sin 2x + C.
ïËÏÎÞÁÔÅÌØÎÏ, ÐÏÄÓÔÁ×ÌÑÑ ÐÏÓÌÅÄÎÉÊ ÒÅÚÕÌØÔÁÔ × (2), ÐÏÌÕÞÉÍ
Z
x
2
cos 2x dx =
1
2
x
2
· sin 2x + x cos 2x −
1
2
sin 2x
+ C =
=
1
2
x
2
sin 2x +
1
2
x cos 2x −
1
4
sin 2x + C.
II. ðÒÉ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÉ ÆÕÎËÃÉÊ ×ÉÄÁ: P
m
(x) arcsin ax, P
m
(x) arccos ax,
P
m
(x) arctg ax, P
m
(x) ln ax × ËÁÞÅÓÔ×Å v
0
(x) ×ÙÂÉÒÁÅÔÓÑ ÍÎÏÇÏÞÌÅÎ P
m
(x), Á
× ËÁÞÅÓÔ×Å u(x) ÏÓÔÁ×ÛÁÑÓÑ ÆÕÎËÃÉÑ.
ðÒÉÍÅÒ 18.
R
x ln x dx. ðÕÓÔØ u(x) = ln x, v
0
(x) = x, ÔÏÇÄÁ
v
0
(x) dx = x dx =
1
2
dx
2
.
Z
x ln x dx =
1
2
Z
ln x dx
2
=
1
2
x
2
ln x −
Z
x
2
d ln x
=
=
1
2
x
2
ln x −
Z
x
2
·
1
x
dx
=
1
2
x
2
ln x −
x
2
2
+ C =
=
x
2
ln x
2
−
x
2
4
+ C.
§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 15
ðÒÉÍÅÒ 19.
R
x arctg 2x dx. ðÕÓÔØ u(x) = arctg 2x, v
0
(x) = x, ÔÏÇÄÁ
Z
x arctg 2x dx =
1
2
Z
arctg 2x dx
2
=
1
2
x
2
· arctg 2x−
−
Z
x
2
d arctg 2x
=
1
2
x
2
arctg 2x −
Z
2x
2
1 + (2x)
2
dx
=
=
1
2
x
2
arctg 2x −
1
2
Z
4x
2
+ 1
4x
2
+ 1
dx +
1
2
Z
1
4x
2
+ 1
dx
=
=
x
2
arctg 2x
2
−
1
4
x +
1
8
Z
d2x
(2x)
2
+ 1
=
x
2
arctg 2x
2
−
1
4
x+
+
1
8
arctg 2x + C.
III. ðÒÉ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÉ ÆÕÎËÃÉÊ e
ax
sin bx, e
ax
cos bx,
√
ax
2
+ b ÉÎÔÅÇÒÉ-
ÒÏ×ÁÎÉÅ ÐÏ ÞÁÓÔÑÍ ÐÒÉÍÅÎÑÅÔÓÑ Ä×Á ÒÁÚÁ. ÷ÙÞÉÓÌÅÎÉÅ ÉÎÔÅÇÒÁÌÁ Ó×ÏÄÉÔÓÑ
Ë ÒÅÛÅÎÉÀ ÁÌÇÅÂÒÁÉÞÅÓËÏÇÏ ÕÒÁ×ÎÅÎÉÑ ÐÅÒ×ÏÊ ÓÔÅÐÅÎÉ.
ðÒÉÍÅÒ 20.
Z
e
x
cos x dx =
Z
cos x de
x
= e
x
cos x −
Z
e
x
d cos x =
= e
x
cos x +
Z
e
x
sin x dx = e
x
cos x +
Z
sin x de
x
=
= e
x
cos x + e
x
sin x −
Z
e
x
d sin x = e
x
cos x + e
x
sin x −
Z
e
x
cos x dx.
ïÂÏÚÎÁÞÉÍ ÞÅÒÅÚ I =
R
e
x
cos x dx. ðÅÒÅÐÉÛÅÍ ÐÏÓÌÅÄÎÅÅ ÒÁ×ÅÎÓÔ×Ï × ×ÉÄÅ:
I = e
x
cos x + e
x
sin x − I,
ÒÅÛÁÑ ÜÔÏ ÕÒÁ×ÎÅÎÉÅ, ÐÏÌÕÞÉÍ
2I = e
x
cos x + e
x
sin x,
I =
1
2
(e
x
cos x + e
x
sin x),
ÏÔÓÀÄÁ ÉÍÅÅÍ:
Z
e
x
cos x dx =
e
x
2
(cos x + sin x) + C.
úÁÍÅÞÁÎÉÅ. ðÒÉ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÉ ÆÕÎËÃÉÊ ×ÉÄÁ e
ax
sin bx, e
ax
cos bx ÉÎ-
ÔÅÇÒÉÒÏ×ÁÎÉÅ ÐÏ ÞÁÓÔÑÍ ÐÒÉÍÅÎÑÅÔÓÑ Ä×Á ÒÁÚÁ, ÐÒÉÞÅÍ × ÏÂÏÉÈ ÓÌÕÞÁÑÈ ×
ËÁÞÅÓÔ×Å ÍÎÏÖÉÔÅÌÑ u(x) ÂÅÒÅÔÓÑ ÆÕÎËÃÉÑ ÏÄÎÏÇÏ É ÔÏÇÏ ÖÅ ÔÉÐÁ: ÐÏËÁÚÁ-
ÔÅÌØÎÁÑ ÉÌÉ ÔÒÉÇÏÎÏÍÅÔÒÉÞÅÓËÁÑ.
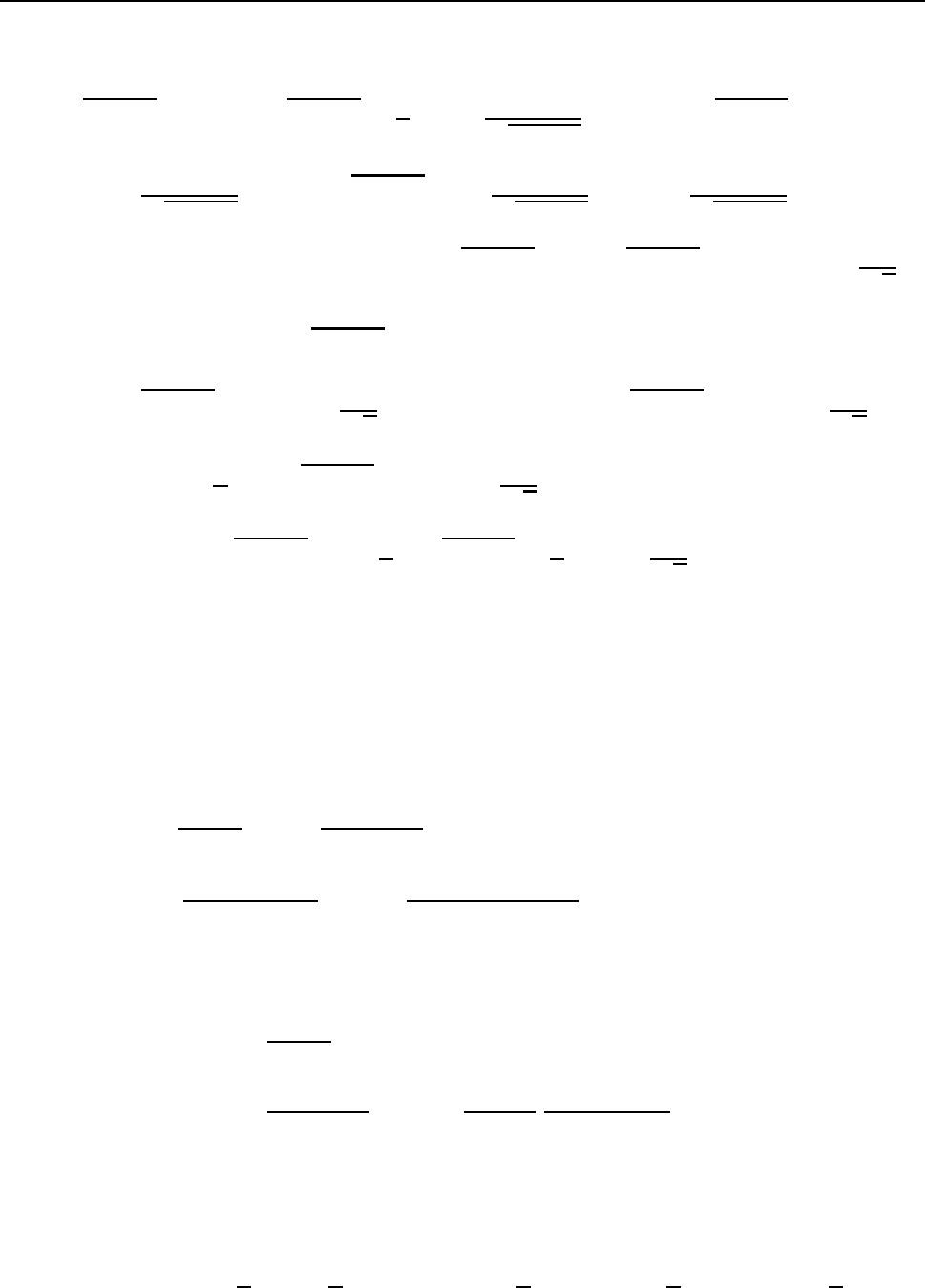
16 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
ðÒÉÍÅÒ 21.
Z
p
7 − x
2
dx = x ·
p
7 − x
2
−
1
2
Z
x ·
(−2x)
√
7 − x
2
dx = x ·
p
7 − x
2
+
+
Z
x
2
√
7 − x
2
dx = x
p
7 − x
2
−
Z
7 − x
2
√
7 − x
2
dx +
Z
7
√
7 − x
2
dx =
= x ·
p
7 − x
2
−
Z
p
7 − x
2
dx + 7 arcsin
x
√
7
.
ïÂÏÚÎÁÞÉÍ ÞÅÒÅÚ I =
R
√
7 − x
2
dx. ðÅÒÅÐÉÛÅÍ ÐÏÓÌÅÄÎÅÅ ÒÁ×ÅÎÓÔ×Ï × ×ÉÄÅ:
I = x
p
7 − x
2
+ 7 arcsin
x
√
7
− I ÉÌÉ 2I = x
p
7 − x
2
+ 7 arcsin
x
√
7
,
I =
1
2
x
p
7 − x
2
+ 7 arcsin
x
√
7
, ÏÔÓÀÄÁ ÉÍÅÅÍ:
Z
p
7 − x
2
dx =
1
2
x
p
7 − x
2
+
7
2
arcsin
x
√
7
+ C.
1.4. éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ÒÁÃÉÏÎÁÌØÎÙÈ ÆÕÎËÃÉÊ
óÎÁÞÁÌÁ ÏÓÔÁÎÏ×ÉÍÓÑ ÎÁ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÉ ÔÁË ÎÁÚÙ×ÁÅÍÙÈ ÐÒÏÓÔÙÈ ÄÒÏ-
ÂÅÊ. üÔÏ ÄÒÏÂÉ ÓÌÅÄÕÀÝÉÈ ÞÅÔÙÒÅÈ ÔÉÐÏ×:
I.
A
x − a
, II.
A
(x − a)
m
,
III.
Ax + B
x
2
+ px + q
, IV.
Ax + B
(x
2
+ px + q)
m
, (m = 2, 3, . . .).
éÎÔÅÇÒÉÒÏ×ÁÎÉÅ ÄÒÏÂÅÊ ×ÉÄÁ I É II ÉÚ×ÅÓÔÎÏ:
I.
Z
A
x − a
dx = A ln |x − a| + C,
II.
Z
A
(x − a)
m
dx = −
A
m − 1
1
(x − a)
m−1
+ C.
ðÒÉ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÉ ÄÒÏÂÅÊ III É IV × ×ÙÒÁÖÅÎÉÉ, ÓÔÏÑÝÅÍ × ÚÎÁÍÅÎÁÔÅÌÅ,
×ÙÄÅÌÑÅÔÓÑ ÐÏÌÎÙÊ Ë×ÁÄÒÁÔ
x
2
+ px + q =
x +
p
2
2
−
p
2
2
+ q =
x +
p
2
2
+
q −
p
2
2
=
x +
p
2
2
+ k.

§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 17
ôÏÇÄÁ ÉÎÔÅÇÒÁÌ ÏÔ ÄÒÏÂÉ III ÚÁÐÉÛÅÔÓÑ × ×ÉÄÅ:
Z
Ax + B
x
2
+ px + q
dx =
Z
Ax + B
x +
p
2
2
+ k
dx =
Z
A
x +
p
2
−
p
2
+ B
x +
p
2
2
+ k
dx =
=
Z
A
x +
p
2
x +
p
2
2
+ k
dx +
Z
B − A ·
p
2
x +
p
2
2
+ k
dx =
Z
At
t
2
+ k
dt +
Z
B − A ·
p
2
t
2
+ k
dt,
ÇÄÅ t = x +
p
2
.
ðÅÒ×ÙÊ ÉÎÔÅÇÒÁÌ ÌÅÇËÏ ×ÙÞÉÓÌÑÅÔÓÑ ÐÏÄÓÔÁÎÏ×ËÏÊ u = t
2
+ k, Á ÉÍÅÎÎÏ:
Z
t dt
t
2
+ k
=
1
2
Z
dt
2
t
2
+ k
=
1
2
Z
d(t
2
+ k)
t
2
+ k
=
1
2
ln |t
2
+ k| + C.
÷ÔÏÒÏÊ ÉÎÔÅÇÒÁÌ
R
dt
t
2
+k
Ñ×ÌÑÅÔÓÑ ÔÁÂÌÉÞÎÙÍ.
ðÒÉ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÉ ÄÒÏÂÉ IV ÁÎÁÌÏÇÉÞÎÏ III ÐÏÌÕÞÉÍ:
Z
Ax + B
(x
2
+ px + q)
m
dx =
Z
Ax + B dx
x +
p
2
2
+ k
m
=
Z
A
x +
p
2
−
p
2
+ B
x +
p
2
2
+ k
m
dx =
= A
Z
t dt
(t
2
+ k)
m
+
B − A ·
p
2
·
Z
dt
(t
2
+ k)
m
.
ðÅÒ×ÙÊ ÉÎÔÅÇÒÁÌ ÌÅÇËÏ ×ÙÞÉÓÌÑÅÔÓÑ ÐÏÄÓÔÁÎÏ×ËÏÊ u = t
2
+ k, Á ÉÍÅÎÎÏ:
Z
t dt
(t
2
+ k)
m
=
1
2
Z
dt
2
(t
2
+ k)
m
=
1
2
Z
d(t
2
+ k)
(t
2
+ k)
m
=
1
2
Z
du
u
m
=
= −
1
2
·
1
m − 1
·
1
u
m−1
+ C = −
1
2(m − 1)
·
1
(t
2
+ k)
m−1
+ C.
÷ÔÏÒÏÊ ÉÎÔÅÇÒÁÌ ×ÙÞÉÓÌÑÅÔÓÑ ÍÅÔÏÄÏÍ ÐÏÎÉÖÅÎÉÑ. ðÕÓÔØ I
m
=
R
dt
(t
2
+k)
m
,
ÔÏÇÄÁ I
m−1
=
R
dt
(t
2
+k)
m−1
.
òÁÓÓÍÏÔÒÉÍ ÉÎÔÅÇÒÁÌ I
m
:
I
m
=
Z
dt
(t
2
+ k)
m
=
1
k
Z
k
(t
2
+ k)
m
dt =
1
k
Z
k + t
2
− t
2
(t
2
+ k)
m
dt =
=
1
k
·
Z
k + t
2
(t
2
+ k)
m
dt −
Z
t
2
(t
2
+ k)
m
dt
=
=
1
k
Z
dt
(t
2
+ k)
m−1
−
Z
t ·
t dt
(t
2
+ k)
m
=
1
k
·
I
m−1
−
1
2
Z
t
d(t
2
+ k)
(t
2
+ k)
m
.
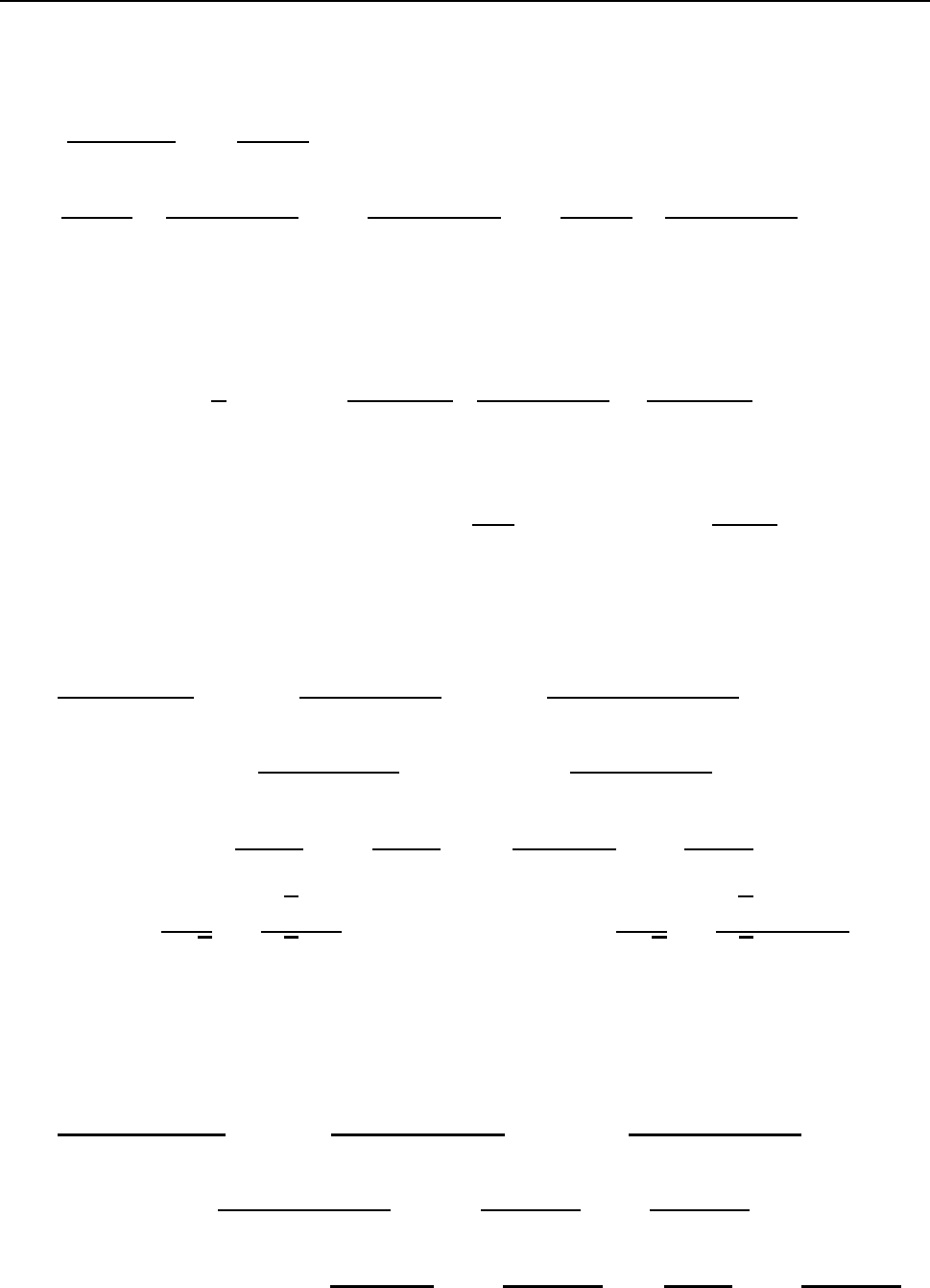
18 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
ðÏÓÌÅÄÎÉÊ ÉÎÔÅÇÒÁÌ ×ÙÞÉÓÌÑÅÔÓÑ ÍÅÔÏÄÏÍ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÐÏ ÞÁÓÔÑÍ:
Z
t
d(t
2
+ k)
(t
2
+ k)
m
= −
1
m − 1
Z
t d(t
2
+ k)
1−m
=
= −
1
m − 1
t
(t
2
+ k)
m−1
−
Z
dt
(t
2
+ k)
m−1
=
1
m − 1
t
(t
2
+ k)
m−1
− I
m−1
.
ïÔÓÀÄÁ ÉÍÅÅÍ, ÞÔÏ
I
m
=
1
k
I
m−1
+
1
2(m − 1)
·
t
(t
2
+ k)
m−1
−
I
m−1
2(m − 1)
.
ðÏÓÌÅÄÎÑÑ ÆÏÒÍÕÌÁ Ó×ÏÄÉÔ ×ÙÞÉÓÌÅÎÉÅ I
m
Ë ×ÙÞÉÓÌÅÎÉÀ I
m−1
. úÎÁÑ ÉÎÔÅ-
ÇÒÁÌ (ÓÍ. ÔÁÂÌÉÃÕ ÉÎÔÅÇÒÁÌÏ×) I
1
=
R
dt
t
2
+k
, ÎÁÊÄÅÍ I
2
=
R
dt
(t
2
+k)
2
É ÔÁË ÄÁÌÅÅ
ÄÏ ÉÎÔÅÇÒÁÌÁ I
m
.
ðÒÉÍÅÒ 22.
Z
2x + 5
x
2
+ 4x − 3
dx =
Z
2x + 5
(x + 2)
2
− 7
dx =
Z
2(x + 2 − 2) + 5
(x + 2)
2
− 7
dx =
=
Z
2 · (x + 2)
(x + 2)
2
− 7
d(x + 2) +
Z
d(x + 2)
(x + 2)
2
− 7
=
= 2
Z
t dt
t
2
− 7
+
Z
dt
t
2
− 7
=
Z
d(t
2
− 7)
t
2
− 7
+
Z
dt
t
2
− 7
=
= ln |t
2
−7|+
1
2
√
7
ln
√
7 − t
√
7 + t
+C = ln |x
2
+4x−3|+
1
2
√
7
ln
√
7 − 2 − x
√
7 + 2 + x
+C.
ðÒÉÍÅÒ 23.
Z
2x + 5
(x
2
+ 4x − 3)
2
dx =
Z
2x + 5
((x + 2)
2
− 7)
2
dx = 2
Z
x + 2
((x + 2)
2
− 7)
2
d(x + 2)+
+
Z
d(x + 2)
((x + 2)
2
− 7)
2
= 2
Z
t dt
(t
2
− 7)
2
+
Z
dt
(t
2
− 7)
2
=
=
Z
d(t
2
− 7)
(t
2
− 7)
2
+
Z
dt
(t
2
− 7)
2
= −
1
t
2
− 7
+
Z
dt
(t
2
− 7)
2
,

§1. îÅÏÐÒÅÄÅÌÅÎÎÙÊ ÉÎÔÅÇÒÁÌ. . . 19
×ÙÞÉÓÌÉÍ ÏÔÄÅÌØÎÏ ÐÏÓÌÅÄÎÉÊ ÉÎÔÅÇÒÁÌ:
Z
dt
(t
2
− 7)
2
= −
1
7
Z
(−7) dt
(t
2
− 7)
2
= −
1
7
Z
t
2
− 7 − t
2
(t
2
− 7)
2
dt =
= −
1
7
Z
t
2
− 7
(t
2
− 7)
2
dt +
1
7
Z
t
2
(t
2
− 7)
2
dt = −
1
7
Z
dt
(t
2
− 7)
+
+
1
14
Z
t
d(t
2
− 7)
(t
2
− 7)
2
= −
1
7
Z
dt
t
2
− 7
−
1
14
Z
t d
1
t
2
− 7
=
= −
1
7
Z
dt
t
2
− 7
−
1
14
t ·
1
t
2
− 7
−
Z
dt
t
2
− 7
=
= −
1
14
Z
dt
t
2
− 7
−
1
14
t
t
2
− 7
=
1
14
·
1
2
√
7
ln
√
7 + t
√
7 − t
−
1
14
t
t
2
− 7
+ C.
ïËÏÎÞÁÔÅÌØÎÏ ÐÏÌÕÞÉÍ:
Z
2x + 5
(x
2
+ 4x − 3)
2
dx = −
1
t
2
− 7
+
1
28
√
7
ln
√
7 + t
√
7 − t
−
1
14
t
t
2
− 7
+ C =
= −
1
x
2
+ 4x − 3
+
1
28
√
7
ln
√
7 + 2 + x
√
7 − 2 − x
−
1
14
x + 2
x
2
+ 4x − 3
+ C.
ðÒÅÖÄÅ ÞÅÍ ÐÅÒÅÊÔÉ Ë ÏÂÝÅÍÕ ÓÌÕÞÁÀ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÐÒÁ×ÉÌØÎÙÈ ÄÒÏ-
ÂÅÊ, ÓÆÏÒÍÕÌÉÒÕÅÍ ÏÄÎÕ ÉÚ ÔÅÏÒÅÍ ÁÌÇÅÂÒÙ, ÉÍÅÀÝÕÀ ÆÕÎÄÁÍÅÎÔÁÌØÎÏÅ
ÚÎÁÞÅÎÉÅ × ÔÅÏÒÉÉ ÉÎÔÅÇÒÉÒÏ×ÁÎÉÑ ÒÁÃÉÏÎÁÌØÎÙÈ ÄÒÏÂÅÊ: ËÁÖÄÁÑ ÐÒÁ×ÉÌØ-
ÎÁÑ ÄÒÏÂØ
P (x)
Q(x)
ÍÏÖÅÔ ÂÙÔØ ÐÒÅÄÓÔÁ×ÌÅÎÁ × ×ÉÄÅ ÓÕÍÍÙ ËÏÎÅÞÎÏÇÏ ÞÉÓÌÁ
ÐÒÏÓÔÙÈ ÄÒÏÂÅÊ.
òÁÚÌÏÖÅÎÉÅ ÐÒÁ×ÉÌØÎÏÊ ÄÒÏÂÉ ÎÁ ÐÒÏÓÔÙÅ ÔÅÓÎÏ Ó×ÑÚÁÎÏ Ó ÒÁÚÌÏÖÅÎÉÅÍ
ÍÎÏÇÏÞÌÅÎÁ Q(x) ÎÁ ÍÎÏÖÉÔÅÌÉ. ëÁË ÉÚ×ÅÓÔÎÏ, ËÁÖÄÙÊ ÃÅÌÙÊ ÍÎÏÇÏÞÌÅÎ Ó
×ÅÝÅÓÔ×ÅÎÎÙÍÉ ËÏÜÆÆÉÃÉÅÎÔÁÍÉ ÒÁÚÌÁÇÁÅÔÓÑ ÎÁ ×ÅÝÅÓÔ×ÅÎÎÙÅ ÍÎÏÖÉÔÅÌÉ
ÔÉÐÁ (x − a) É (x
2
+ px + q). ÷ ÓÈÅÍÁÔÉÞÅÓËÏÍ ×ÉÄÅ ÒÁÚÌÏÖÅÎÉÅ ÍÎÏÇÏÞÌÅÎÁ
Q(x) ÍÏÖÎÏ ÚÁÐÉÓÁÔØ × ×ÉÄÅ: Q(x) = (x−a)
k
·. . .·(x
2
+px+q)
m
. ðÏËÁÖÅÍ, ËÁË,
Ó ÕÞÅÔÏÍ ÒÁÚÌÏÖÅÎÉÑ Q(x), ÐÒÁ×ÉÌØÎÁÑ ÄÒÏÂØ ÒÁÓËÌÁÄÙ×ÁÅÔÓÑ ÎÁ ÐÒÏÓÔÙÅ:
1. åÓÌÉ ÍÎÏÖÉÔÅÌØ (x − a) ×ÈÏÄÉÔ × ÒÁÚÌÏÖÅÎÉÅ Q(x) ÔÏÌØËÏ × ÐÅÒ×ÏÊ
ÓÔÅÐÅÎÉ, ÍÙ ÐÏÓÔÁ×ÉÍ ÅÍÕ × ÓÏÏÔ×ÅÔÓÔ×ÉÅ ÅÄÉÎÓÔ×ÅÎÎÕÀ ÐÒÏÓÔÕÀ ÄÒÏÂØ:
(x − a) →
A
x − a
.
2. åÓÌÉ × ÒÁÚÌÏÖÅÎÉÅ Q(x) ×ÈÏÄÉÔ ÍÎÏÖÉÔÅÌØ (x−a)
k
, ÔÏ ÅÓÔØ ÐÏËÁÚÁÔÅÌØ
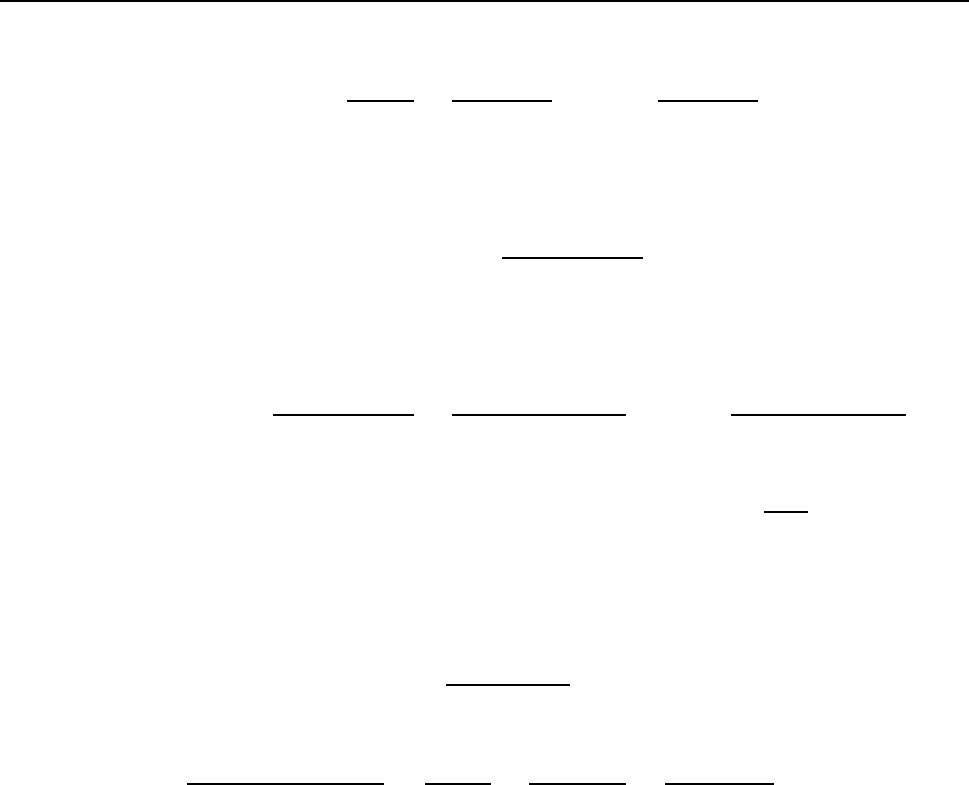
20 çÌÁ×Á I. éÎÔÅÇÒÁÌØÎÏÅ ÉÓÞÉÓÌÅÎÉÅ ÆÕÎËÃÉÉ ÏÄÎÏÊ ÐÅÒÅÍÅÎÎÏÊ
ÓÔÅÐÅÎÉ k > 1, ÔÏ ÅÍÕ ÓÏÏÔ×ÅÔÓÔ×ÕÅÔ ÓÕÍÍÁ ÉÚ k ÐÒÏÓÔÙÈ ÄÒÏÂÅÊ
(x − a)
k
→
A
1
x − a
+
A
2
(x − a)
2
+ . . . +
A
k
(x − a)
k
.
3. åÓÌÉ × ÒÁÚÌÏÖÅÎÉÅ Q(x) ×ÈÏÄÉÔ ÍÎÏÖÉÔÅÌØ x
2
+ px + q ÔÏÌØËÏ × ÐÅÒ×ÏÊ
ÓÔÅÐÅÎÉ, ÔÏ × ÓÏÏÔ×ÅÔÓÔ×ÉÅ ÅÍÕ ÓÔÁ×ÉÔÓÑ ÅÄÉÎÓÔ×ÅÎÎÁÑ ÐÒÏÓÔÁÑ ÄÒÏÂØ:
x
2
+ px + q →
Mx + N
x
2
+ px + q
.
4. åÓÌÉ × ÒÁÚÌÏÖÅÎÉÅ Q(x) ×ÈÏÄÉÔ ÍÎÏÖÉÔÅÌØ (x
2
+ px + q)
k
, ÐÏËÁÚÁÔÅÌØ
ËÏÔÏÒÏÇÏ k > 1, ÔÏ ÅÍÕ ÓÏÏÔ×ÅÔÓÔ×ÕÅÔ ÓÕÍÍÁ ÉÚ k ÐÒÏÓÔÙÈ ÄÒÏÂÅÊ
(x
2
+ px + q)
k
→
M
1
x + N
1
x
2
+ px + q
+
M
2
x + N
2
(x
2
+ px + q)
2
+ . . . +
M
k
x + N
k
(x
2
+ px + q)
k
.
äÌÑ ÎÁÈÏÖÄÅÎÉÑ ÎÅÉÚ×ÅÓÔÎÙÈ ËÏÜÆÆÉÃÉÅÎÔÏ× A, M, N ÉÓÐÏÌØÚÕÀÔ ÍÅÔÏÄ
ÎÅÏÐÒÅÄÅÌÅÎÎÙÈ ËÏÜÆÆÉÃÉÅÎÔÏ×. úÎÁÑ ÆÏÒÍÕ ÒÁÚÌÏÖÅÎÉÑ
P (x)
Q(x)
ÎÁ ÐÒÏÓÔÙÅ
ÄÒÏÂÉ, ÐÉÛÕÔ ÅÇÏ Ó ÂÕË×ÅÎÎÙÍÉ ËÏÜÆÆÉÃÉÅÎÔÁÍÉ ÓÐÒÁ×Á. ðÒÉ×ÏÄÑÔ ÄÒÏÂÉ
Ë ÏÄÎÏÍÕ ÚÎÁÍÅÎÁÔÅÌÀ Q(x) É ÐÒÉÒÁ×ÎÉ×ÁÀÔ ÍÎÏÇÏÞÌÅÎÙ, ÓÔÏÑÝÉÅ × ÞÉ-
ÓÌÉÔÅÌÑÈ ÓÐÒÁ×Á É ÓÌÅ×Á. úÁÔÅÍ, ÐÒÉÒÁ×ÎÉ×ÁÑ ËÏÜÆÆÉÃÉÅÎÔÙ, ÓÔÏÑÝÉÅ ÐÒÉ
ÏÄÉÎÁËÏ×ÙÈ ÓÔÅÐÅÎÑÈ, ÎÁÈÏÄÑÔ ÎÅÉÚ×ÅÓÔÎÙÅ ÂÕË×ÅÎÎÙÅ ËÏÜÆÆÉÃÉÅÎÔÙ.
ðÒÉÍÅÒ 24. òÁÚÌÏÖÉÔØ ÄÒÏÂØ
2x
2
+2x+13
(x−2)(x
2
+1)
2
ÎÁ ÐÒÏÓÔÙÅ.
ðÒÅÄÓÔÁ×ÉÍ ÄÒÏÂØ × ×ÉÄÅ:
2x
2
+ 2x + 13
(x − 2)(x
2
+ 1)
2
=
A
x − 2
+
Bx + C
x
2
+ 1
+
Dx + E
(x
2
+ 1)
2
.
ëÏÜÆÆÉÃÉÅÎÔÙ A, B, C, D, E ÏÐÒÅÄÅÌÉÍ, ÉÓÈÏÄÑ ÉÚ ÔÏÖÄÅÓÔ×Á:
2x
2
+ 2x + 13 = A · (x
2
+ 1)
2
+ (Bx + C)(x
2
+ 1)(x − 2) + (Dx + E)(x − 2),
ÏÔÓÀÄÁ ÐÏÌÕÞÉÍ:
2x
2
+ 2x + 13 = (A + B) · x
4
+ (C − 2B) · x
3
+ (2A + B − 2C + D) · x
2
+
+ (C − 2B + E − 2D) ·x + A − 2C − 2E.
ðÒÉÒÁ×ÎÉ×ÁÑ ËÏÜÆÆÉÃÉÅÎÔÙ ÐÒÉ ÏÄÉÎÁËÏ×ÙÈ ÓÔÅÐÅÎÑÈ x ÓÌÅ×Á É ÓÐÒÁ×Á,
ÐÒÉÄÅÍ Ë ÓÉÓÔÅÍÅ ÉÚ ÐÑÔÉ ÕÒÁ×ÎÅÎÉÊ
A + B = 0,
−2B + C = 0,
2A + B − 2C + D = 2,
−2B + C − 2D + E = 2,
A − 2C −2E = 13,
ÏÔËÕÄÁ
A = 1, B = −1, C = −2, D = −3, E = −4.
