Давыдова В.Н., Мунш Т.А., Бадюля А.П. Mathcad в химической технологии
Подождите немного. Документ загружается.

41
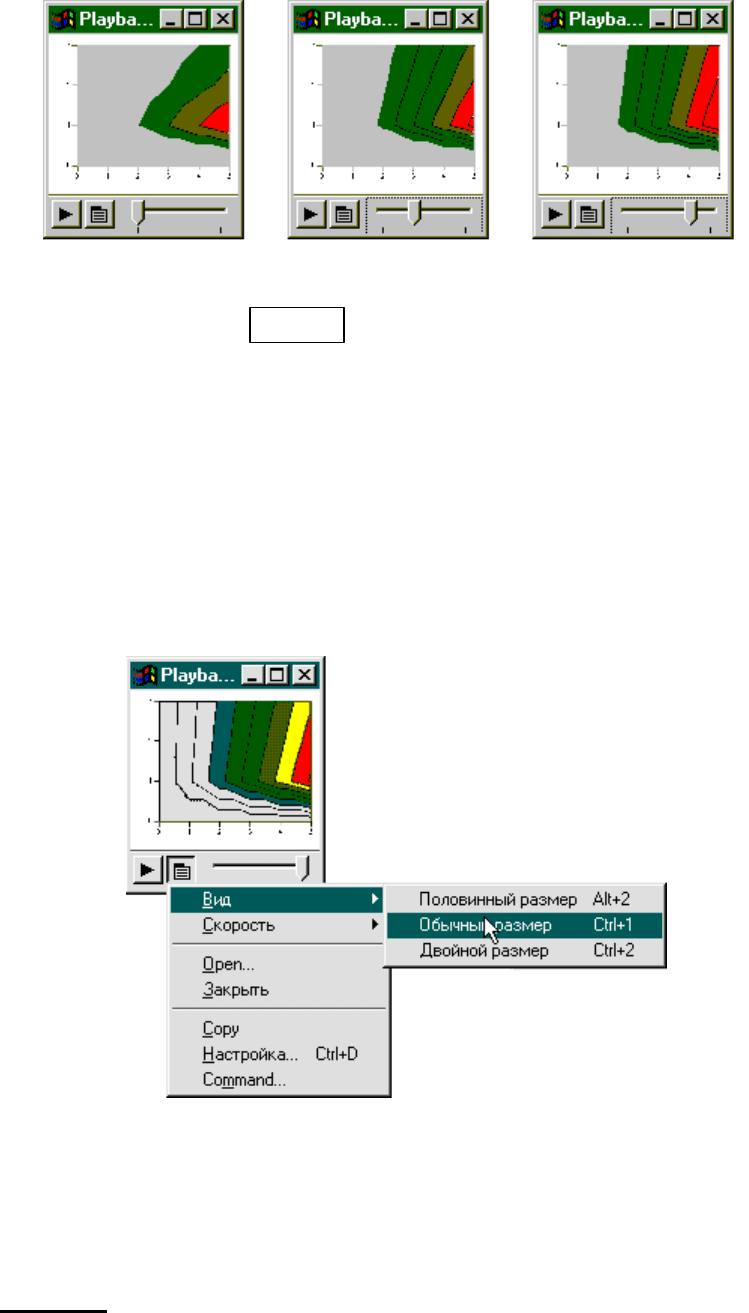
Рис. 47
Щелкнув на кнопке Save as (сохранить как), можно вызвать стандарт-
ное окно записи файлов на диск. Файл записывается с расширением .avi, при-
нятым для файлов программной видеосистемы Microsoft Video for Windows.
Окно Playback содержит дополнительную кнопку, нажатие на которую
выводит меню. С его помощью регулировать некоторые параметры воспро-
изведения (рис. 48).
Рис. 48
Щелкнув в окне проигрывателя на кнопке с изображением треугольни-
ка, можно наблюдать изменение графика во времени.
Задача 7 [4, стр. 234 – 238]. Расчет образования кокса

42
Образование кокса
C
протекает как стадийный процесс превращения
сырья
R
с образованием в качестве промежуточного продукта «полукокса»
S
вещества, растворимого в бензоле, и низкомолекулярных относительно
сырья летучих продуктов
V
по схеме:
C
S
R
V
.
Было предложено сырье рассматривать как двухкомпонентное: первый
компонент
1
R – это основная масса сырья, являющаяся коксогенной, а вто-
рой
2
R проявляет активность в образовании летучих продуктов. Необходимо
также учесть, что в ходе коксования полукокс частично образует летучие
продукты
V
. Принимая, что все реакции протекают по первому порядку,
имеем для изменения концентраций компонентов:
151
1
)(
R
R
ckk
d
dc
22
2
R
R
ck
d
dc
SSR
S
ckckck
d
dc
3411
S
C
ck
d
dc
3
22415 RSR
V
ckckck
d
dc
со следующими начальными условиями:
0
2010
RR
cc , 0
SVC
ccc .
Построить графики функций изменения концентраций компонентов во
времени, если известны значения параметров:
3
1
103,1
k ,
3
2
107,6
k ,
3
3
109,2
k ,
3
4
106,3
k ,
4
5
105,5
k , 50,0
10
R
c .
Методика расчета.
Целесообразно провести замену переменных:
01
yc
R
,
1
2
yc
R
,
2
yc
S
,
3
yc
C
,
4
yc
V
.
43
Системы обыкновенных дифференциальных уравнений (ОДУ) для их
решения в среде Mathcad должны быть представлены в форме Коши:
nn
yxy
yxy
yxy
,00
2,002
1,001
)(
...................
)(
)(
,
),...,,,(
.......................................
),...,,,(
),...,,,(
21
2122
2111
nnn
n
n
yyyxfy
yyyxfy
yyyxfy
Первая система задает начальные условия, а вторая представляет сис-
тему ОДУ. В векторном виде система выглядит так:
).,(
)(
00
YxFY
YxY
Решение системы ОДУ, таким образом, должно быть организовано в
векторной форме.
Для решения задач такого класса в Mathcad введен ряд функций:
1) rkadapt(y,x1,x2,acc,n,F,k,s) – возвращает матрицу, содержащую таб-
лицу значений решения на интервале от x1 до x2 для ОДУ, вычисленную ме-
тодом Рунге – Кутта с переменным шагом и начальными условиями в векто-
ре y (правые части системы записаны в векторе F, n – число шагов, k –
максимальное число промежуточных точек решения, s – минимально допус-
тимый интервал между точками);
2) Rkadapt(y,x1,x2,n,F) – возвращает матрицу решений методом Рунге –
Кутта с переменным шагом для ОДУ с начальными условиям в векторе y,
правые части которых записаны в символьном векторе F на интервале от x1
до x2 при фиксированном числе шагов n;
3) rkfixed (y,x1,x2,n,F) – аналогично Rkadapt с тем лишь отличием, что
шаг является постоянным.
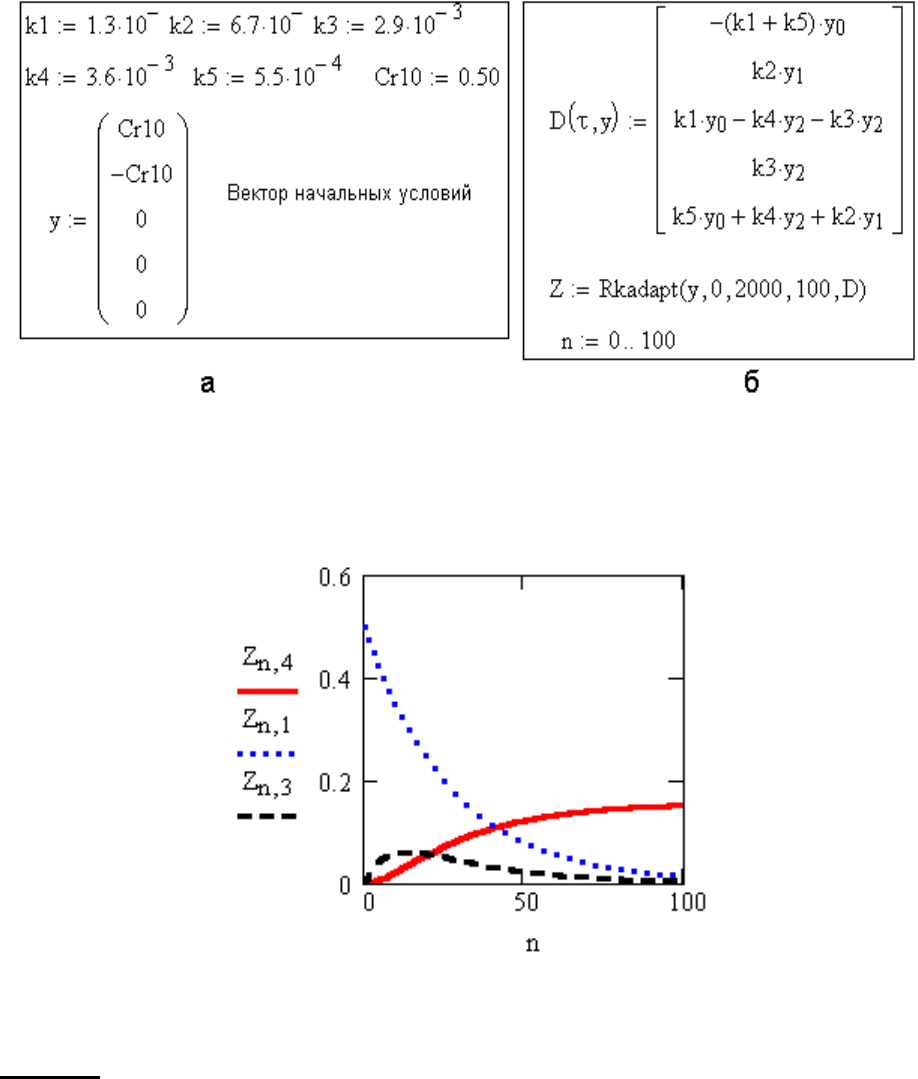
Рис. 49 последовательно иллюстрирует технику решения исходной сис-
темы уравнений (блок на рис. 49а должен предшествовать блоку на рис. 49б).
44
Рис. 49
На рис. 50 представлены решения для концентраций
10R
c ,
S
c ,
V
c .
Рис. 50
Задача 8 [5, стр. 123 – 129]. Расчет приземных концентраций вредных
веществ
Одна из методик расчета концентраций вредных веществ в приземном
слое атмосферы позволяет оценить максимальную разовую концентрацию
при опасной скорости ветра, т.е. такой скорости, при которой возникает наи-
большее значение приземной концентрации вещества, поступившего из оди-
ночного источника. Если имеется несколько источников выбросов вредного

45
вещества, то рассчитывается средняя для рассматриваемой совокупности ис-
точников опасная скорость ветра. В результате расчетов находят условия,
при которых приземная концентрация вредных веществ, обусловленная вы-
бросами, была бы меньше ПДК.
Максимальная приземная концентрация вредных веществ
i
M
C (мг/м
3
)
в выбросе газовоздушной смеси из одиночного источника с круглым усть-
ем при неблагоприятных метеорологических условиях и опасной скорости
ветра равна
3
2
iii
ii
i
M
TVH
FmAM
C
Здесь
A
– климатологический фактор,
i
M – количество вредного ве-
щества, выбрасываемого в атмосферу, г/с,
F
– параметр, характеризующий
оседание примесей,
i
H – высота трубы источника, м,
i
V – объем газовоз-
душной смеси, выбрасываемой в атмосферу в единицу времени, м
3
/с,
вii
TTT
– разность между температурой выбрасываемой смеси
i
T и тем-
пературой воздуха
в
T .
Коэффициент
i
m , учитывающий условия выхода смеси из устья источ-
ника, рассчитывается по формуле:
3
34,01,067,0
1
ii
i
ff
m
;
ii
ii
i
TH
D
f
2
2
3
10
,
2
4
i
i
i
D
V
где
i
– средняя скорость смеси на выходе из устья (отверстия) тру-
бы, м/с,
i
D диаметр отверстия трубы, м.
Максимальная приземная концентрация одного вещества определяется
как
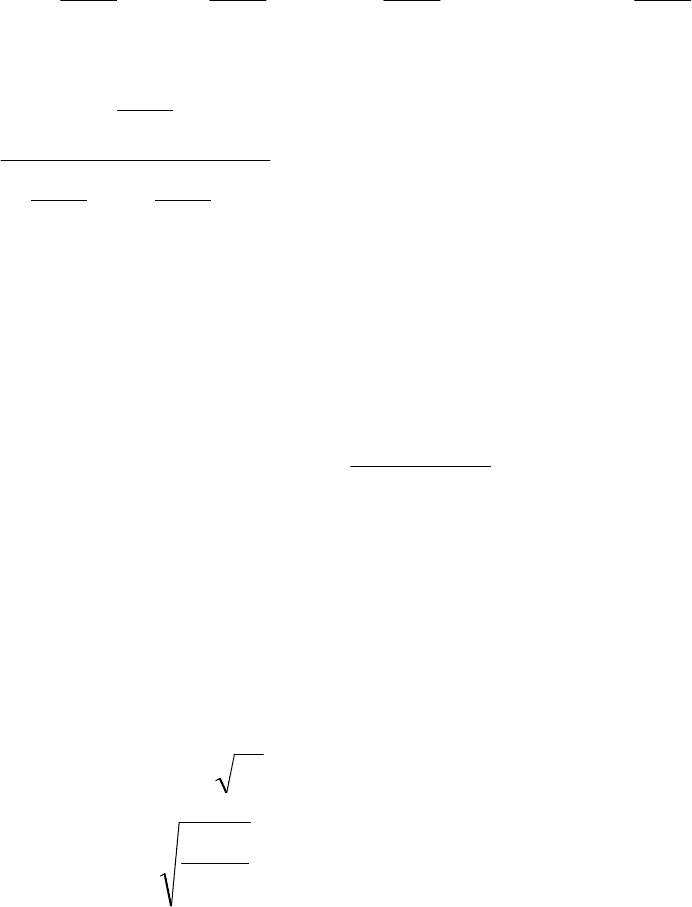
46
ii
MiMu
CrС
32
)(34,1)(67,167,0
iii
M
MC
M
MC
M
MC
i
u
u
u
u
u
u
r при условии 1
i
M
MC
u
u
, и
2)()(2
3
2
ii
i
M
MC
M
MC
M
MC
i
u
u
u
u
u
u
r — в противном случае.
Средняя для рассматриваемой совокупности источников опасная ско-
рость ветра
MC
u (м/с) рассчитывается по формуле:
n
i
M
n
i
MM
MC
i
ii
C
Cu
u
1
1
При расчетах принимают:
1)
5,0
i
M
u
при условии, что
5,0
i
M
;
2)
ii
MM
u
при условии, что
22
i
M
;
3)
)12,01(
iMM
fu
ii
при условии, что
2
i
M
.
Здесь
3
65,0
i
i
M
H
TV
i
Суммарная концентрация примеси:
n
i
MuMU
i
CC
1
В качестве примера рассмотрим расчет загрязнения атмосферы диокси-
дом серы от установок нефтеперерабатывающего завода. Источниками загряз-
нения являются: 1) установка каталитического риформинга; 2) установка тер-

47
мического крекинга; 3) установка гидроочистки; 4) атмосферно-вакуумная
трубчатка; 5) установка по производству серы из сероводорода.
Фоновую концентрацию диоксида серы, которая имеет место в отсут-
ствие установок, примем равной нулю. Трубы всех пяти установок имеют
равную высоту.
Решим задачу с использованием программных средств MathCad. Набор
инструкций для создания программных модулей содержит следующие эле-
менты:
1) Add Line – создает и при необходимости удлиняет жирную верти-
кальную линию, справа от которой в местах ввода задается запись программ-
ного блока;
2) – символ локального присваивания (в теле модуля);
3) if – условная инструкция;
4) for – инструкция задания цикла с фиксированным числом повторений;
5) while – инструкция задания цикла, действующего до тех пор, пока
выполняется некоторое условие;
6) otherwise – инструкция иного выбора (обычно применяется с if);
7) break – инструкция прерывания;
8) continue – инструкция продолжения;
9) return – инструкция возврата;
10) on error – инструкция обработчика ошибок.
Все эти инструменты сгруппированы на панели «Programming» (рис. 51),
которая выводится на экране нажатием кнопки
Рис. 51

48
Идея решения задачи заключается в постепенном увеличении высоты
трубы до тех пор, пока суммарная концентрация вредных выбросов не станет
меньше определенного пользователем ПДК.
Прежде всего, необходимо определить несколько вспомогательных
функций, которые будут использоваться при расчете. На рис. 52 представле-
но традиционное однозначное определение функции. Такое описание позво-
ляет получить значение функции для любого аргумента.
Рис. 52
Кроме того, нам понадобятся две функции, вычисление которых зави-
сит от конкретных значений аргументов. Для их задания понадобятся инст-
рументы программирования (рис. 53).
Рис. 53
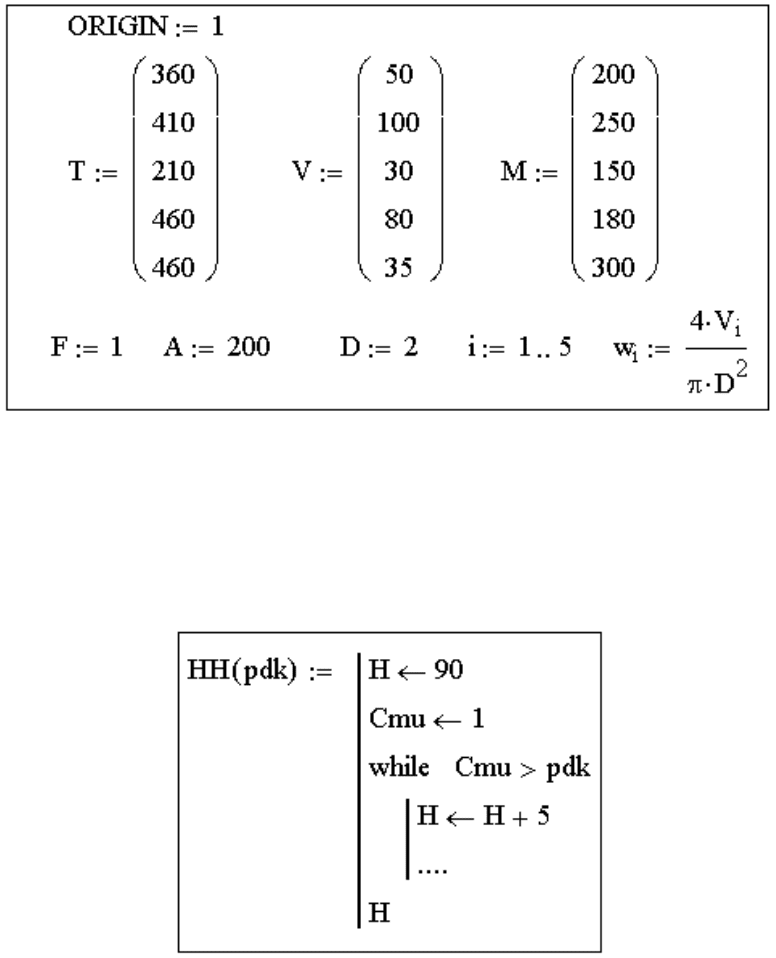
Далее, определив все необходимые переменные (рис. 54), можно при-
ступать непосредственно к расчету. Здесь следует обратить внимание на то,
49
что величина
i
не зависит от высоты трубы
H
, поэтому эту формулу целе-
сообразно вынести за пределы функции.
Рис. 54
Функция HH, которая принимает определенное значение ПДК и воз-
вращает оптимальное для нее высоту трубы, будет иметь следующую струк-
туру (рис. 55):
Рис. 55
Локальным переменным H и Cmu присваиваются начальные значения.
Далее в цикле происходит постепенное увеличение высоты трубы на 5 мет-
ров до тех пор, пока не будет выполнено условие. Сформированное таким
образом значение H возвращается пользователю.
50
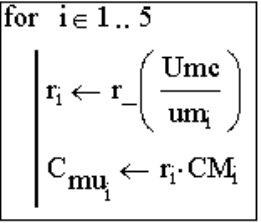
При реализации алгоритма следует помнить, что для расчета векторных
переменных необходимо вводить дополнительные циклы (рис 56).
Рис. 56
Полностью алгоритм представлен на рис. 57. Теперь, непосредственно
используя эту функцию, можно определить, что для ПДК=0,5 все трубы
должны иметь высоту не менее 135 м (HH(0.5)=135), а для ПДК=0,9 – 100 м
(HH(0.9)=100).
Следует отметить, что можно было бы получать и более «точную»
высоту. Для этого можно изменить шаг наращивания высоты трубы. Так,
если сделать его равным 1 м, то HH(0.9)=98. Однако всегда следует пом-
нить о разумном компромиссе между возможностями ЭВМ и задачей
предметной области – при реальном строительстве объектов используются
более крупные шаги.
