Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

10.6 Characterizing Best Approximations 303

endpoints). Notice that since each I

has length less than δ, if r(x) = R for some

x ∈ I

, then for all y ∈ I

we have

r(y) ≥ r(x) − |r(x) − r(y)| ≥ R/2.

Similarly, if r(x) = −R for some x ∈ I

, then r(y) ≤ −R/2 for all y ∈ I

. Let ε

be +1 or −1 according to whether r(x) is positive or negative on I

CLAIM: The sequence (ε

, . . . , ε

) has at least n + 1 changes of sign.

Accepting this claim for a moment, we produce the points required in the def-

inition of the equioscillation condition. Group together adjacent intervals with the

same sign, and label them J

, J

, . . . , J

, where k ≥ n + 2. For each i between 1

and n + 2, pick a point x

∈ J

so that |r(x

)| = R. By the choice of J

, the signs

alternate and so the equioscillation condition holds.

Thus, it remains only to prove the claim. Suppose the claim is false; that is,

there are at most n changes of sign in (ε

, . . . , ε

). We will construct a better

approximating polynomial, contradicting the choice of p.

Again, group together adjacent intervals with the same sign, and label them

, J

, . . . , J

, where k ≤ n + 1. Because f changes sign between J

and J

i+1

, it

is possible to pick a point a

∈ R that lies in between. Deﬁne a polynomial q of

degree k − 1 ≤ n by

q(x) =

k−1

i=1

x − a

As q ∈ P

and q changes sign at each a

, either q or −q agrees in sign with r(x)

on each set J

, i = 1, . . . , k. If necessary, replace q with −q so that this agreement

holds.

Let L

j=1

and L

[a, b]\L

. Since L

is compact and q is never zero

on L

, the minimum,

m = min{|q(x)| : x ∈ L

}

is strictly positive by the Extreme Value Theorem. Let M = kqk

∞

Since L

is compact and each I

has been removed from L

, |r(x)| does not

attain the value R on L

. Again using the Extreme Value Theorem, there is some

d > 0 so that

max{|r(x)| : x ∈ L

} = R − d < R.

We will show that the polynomial

s(x) = p(x) +

q(x)

is a better approximation to f than p(x), contradicting the choice of p. Notice that

f(x) − s(x) = r(x) −

q(x).

Because r and q have the same sign on each I

max

x∈L

|f(x) − s(x)| ≤ R −

304 Approximation by Polynomials

On the remainder, we have

max

x∈L

|f(x) − s(x)| ≤ max

x∈L

|f(x) − p(x)| + max

x∈L

|p(x) − s(x)|

≤ R − d +

kqk = R −

Now [a, b] = L

∪ L

. Thus

kf − sk = max

a≤x≤b

|f(x) − s(x)| ≤ max

R −

, R −

< R.

This contradicts the minimality of p and so proves the claim. ¥

Let us put these results together with one more idea to complete the main result.

10.6.6. CHEBYCHEV APPROXIMATION THEOREM.

For each continuous function f in C[a, b], there is a unique polynomial p of degree

at most n so that

kf − pk

∞

= inf{kf − qk

∞

: q ∈ P

[a, b]}.

This best approximant is characterized by the fact that f −p either is 0 or satisﬁes

the equioscillation condition of degree n.

PROOF. By Theorem 10.5.3, there is at least one closest polynomial to f in P

Suppose p, q ∈ P

are both closest polynomials in P

, and let

R = kf − pk

∞

= kf − qk

∞

Then the midpoint (p+q)/2 is also a polynomial in P

which is closest to f because

of the triangle inequality:

R ≤

f −

p + q

∞

≤

kf − pk

∞

kf − qk

∞

= R.

Thus by Theorem 10.6.5, r = f −

(p + q) satisﬁes the equioscillation condi-

tion. Let x

< x

< ··· < x

n+2

be the required points such that

|f(x

) − r(x

)| = R for 1 ≤ i ≤ n + 2.

Another use of the triangle inequality yields

R =

f(x

) −

p(x

) + q(x

)

≤

f(x

) − p(x

)

f(x

) − q(x

)

≤ R.

Consequently, f(x

) − p(x

) and f (x

) − q(x

) both have absolute value R. Since

there is no cancellation when they are added, they must have the same sign. There-

fore, f(x

) − p(x

) = f (x

) − q(x

), and hence

p(x

) = q(x

) for 1 ≤ i ≤ n + 2.

Therefore, p − q is a polynomial of degree at most n with n + 2 roots; and so is

identically equal to zero. In other words, the closest point is unique. ¥

10.6 Characterizing Best Approximations 305

10.6.7. EXAMPLE. Chebychev’s characterization sometimes allows exact cal-

culation of the best polynomial. Consider the question: Find the closest cubic to

f(x) = cosx on [−

Since f is an even function, we expect that the best approximation will be even.

This is indeed the case. Let p ∈ P

be the closest cubic, and let ˜p(x) = p(−x).

Then

kf − ˜pk

∞

= max

−1≤x≤1

|f(x) − p(−x)|

= max

−1≤x≤1

|f(−x) − p(−x)| = kf − pk

∞

As the closest polynomial is unique, it follows that p = ˜p, namely p(−x) = p(x).

So we are looking for p(x) = ax

+ b.

From Chebychev’s Theorem, we are looking for a polynomial that differs from

f by ±d at 5 points with alternating signs, where d = kf − pk

∞

. Consider the

derivatives of r(x) = cos x − ax

− b.

(x) = −sin x − 2ax and r

(x) = −cos x − 2a

Since −cosx is concaveon [−

], the second derivative r

has at most two zeros.

This happens only if −

< a < 0; and these zeros are at ±z = ±cos

−1

(2a). So

is decreasing on [−1, −z], then increasing on [−z, z], and then decreasing again

on [z, 1]. Thus r

can have at most three zeros. But r achieves its extreme values

ﬁve times. So r

has exactly three zeros corresponding to extrema of r; and the

other two extrema must be at the endpoints. Because of the symmetry of even

functions, one extremum is at 0, and the other two critical points will be called

±x

. Moreover, r

(0) = 0 and r

(0) = −1 −2a < 0; so this is a maximum.

So far, we have

d = r(0) = 1 − b

d = r(±

) = −a

− b

−d = r(±x

) = cos x

− ax

− b

0 = r

) = −sin x

− 2ax

Solving the ﬁrst two equations for a yields

a = −

Plugging this into the fourth yields

sinx

Since sin x is concave on [0,

], this equation has a unique positive solution. It

may be found numerically to be approximately x

:= 1.0988243. From the third

equation (and the ﬁrst), we obtain

b =

(1 + cos x

) := 0.9719952.

306 Approximation by Polynomials

So the closest cubic to cos x on [−

] is p(x) = −

+ 0.9719952 and the

error is d = 0.0280048.

Exercises for Section 10.6

A. Find the closest line to e

on [0, 1].

B. Find the cubic polynomial which best approximates |x| on the interval [−1, 1].

HINT: Use symmetry ﬁrst.

C. Suppose that f ∈ C[a, b] is a twice continuously differentiable function with f

(x) >

0 on [a, b]. Show that the best linear approximation to f has slope

f(b) − f(a)

b − a

D. Apply the previous exercise to ﬁnd the closest line to f(x) =

√

1 + 3x

on [0, 1], and

compute the error.

E. If f in C[−1, 1] is an even (odd) function, show that the best approximation of degree

n is also even (odd).

F. Let p be the best polynomial approximation of degree n to

√

x on [0, 1]. Show that

q(x) = p(x

) is the best polynomial approximation of degree 2n + 1 to |x| on [−1, 1].

HINT: How does the equioscillation condition on

√

x − p(x) translate to the approxi-

mation of |x|?

10.7. Expansions Using Chebychev Polynomials

Ideally, we would like to ﬁnd the polynomial that is exactly the best approx-

imation to a given continuous function f. There is an algorithm that constructs a

sequence of polynomials converging uniformly to the best approximating polyno-

mial of degree n known as Remes’s algorithm. Roughly, it works as follows: Pick

n + 2 points x

< x

< . . . x

n+2

in [a, b]. These points might be equally spaced,

but foreknowledge of the function could lead you to pick points clustered in regions

where f behaves more wildly. Then solve the linear equations for a

, a

, . . . , a

and d:

+ x

+ . . . + x

− d = f(x

)

+ x

+ . . . + x

+ d = f(x

)

+ x

n+2

+ x

n+2

+ . . . + x

n+2

+ (−1)

n+2

d = f(x

n+2

This method attempts to ﬁnd a polynomial that satisﬁes Chebychev’s Theorem.

However, the function may well take its extrema on other points. So the algorithm

proceeds to choose new points x

, . . . , x

n+2

by selecting points where the error is

largest (or close to it) near each point. Eventually, this procedure converges to the

nearest polynomial of degree n.

10.7 Expansions Using Chebychev Polynomials 307

However, each step of this process involves many calculations, so convergence

to the optimal polynomial is slow. In practice, it is better to ﬁnd quickly an approx-

imating polynomial that is not quite the best. It is often easier to ﬁnd a polynomial

of say double the degree with half the accuracy, rather than seeking the optimal so-

lution. Solutions that are less than optimal, but still quite good, can be found very

efﬁciently. We develop such an algorithm in this section using Chebychev polyno-

mials. Chebychev polynomials are also useful in numerical analysis, algebra, and

other areas.

10.7.1. DEFINITION. For n ≥ 0, deﬁne the Chebychev polynomial of degree

n in P

[−1, 1] by

(x) = cos(n cos

−1

x).

It is not immediately obvious that T

is a polynomial, much less a polynomial

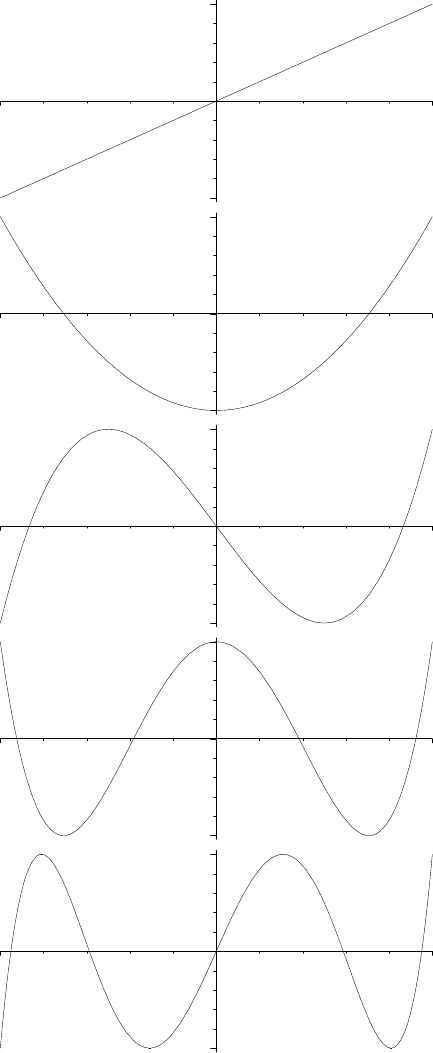
of degree n. Figure 10.5 gives the graphs of T

through T

on [−1, 1]. The T in T

comes from Tchebycheff, an earlier transliteration of Chebychev from the original

Russian.

10.7.2. LEMMA. T

(x) = 1, T

(x) = x and

(x) = 2xT

n−1

(x) − T

n−2

(x) for n ≥ 2.

For each n ≥ 1, T

(x) is a polynomial of degree n with leading coefﬁcient 2

n−1

Also, kT

∞

= 1, and

cos

¢¢

= (−1)

for 0 ≤ k ≤ n.

PROOF. Recall the sum and difference of angles formulas for cosine:

cos(A + B) = cosA cosB − sinA sin B

and

cos(A − B) = cosA cosB + sinA sinB.

Let A = nθ and B = θ, and add these formulas to get

cos(n + 1)θ + cos(n − 1)θ = 2cosnθ cosθ.

Substituting θ = cos

−1

x gives

n+1

(x) + T

n−1

(x) = 2xT

(x) for all n ≥ 1.

Evidently, T

= 1 and T

(x) = x. The next few terms are

(x) = 2xT

(x) − T

(x) = 2x

− 1,

(x) = 2xT

(x) − T

(x) = 4x

− x,

(x) = 2xT

(x) − T

(x) = 8x

− 8x

+ 1,

(x) = 2xT

(x) − T

(x) = 16x

− 20x

+ 5x.

By induction, it follows that T

(x) is a polynomial of degree n with leading coef-

ﬁcient 2

n−1

308 Approximation by Polynomials

–1

–1 1

–1

–1 1

–1

–1 1

–1

–1 1

–1

–1 1

FIGURE 10.5. The Chebychev polynomials T

through T

10.7 Expansions Using Chebychev Polynomials 309

Since |cosθ| ≤ 1 for all values of θ, it follows that kT

∞

≤ 1. Now

|cos(θ)| = 1 only when θ is an integer multiple of π. It follows that T

attains

its maximum modulus when n cos

−1

x = kπ for some integer k. Solving, we

obtain

= cos

for 0 ≤ k ≤ n.

Other choices of k just repeat these values. Finally,

) = (−1)

for 0 ≤ k ≤ n. ¥

10.7.3. COROLLARY. The unique polynomial of degree at most n −1 that best

approximates x

on [−1, 1] is p

(x) = x

− 2

1−n

(x), and E

n−1

) = 2

1−n

PROOF. Since the leading term of T

is 2

n−1

, p

(x) is a polynomial of degree

at most n − 1. The difference

− p

(x) = 2

1−n

(x)

has maximum modulus 2

1−n

, and it attains this maximum modulus at the n + 1

points x

= cos(kπ/n) for 0 ≤ k ≤ n with alternating sign. Hence it satisﬁes

the equioscillation condition of degree n −1. By Chebychev’s Theorem, this is the

unique closest polynomial of degree n − 1. ¥

Without developing any further results, we can already use Chebychev polyno-

mials to ﬁnd good approximations.

10.7.4. EXAMPLE. We will approximate f(x) = sin(x) on the interval [−1, 1]

by modifying the Taylor approximations. The Taylor polynomial of degree 10 is

p(x) = x −

−

For x ∈ [−1, 1], the error term is given by Taylor’s Theorem,

|sin(x) − p(x)| ≤

|x|

11!

(11)

∞

≤

11!

< 2.506 × 10

−8

The idea is to replace the term x

/9! with the best approximation of degree less

than 9, which we have seen is (x

− T

(x)/2

)/9!. This increases the error by at

most

−

− T

(x)/2

∞

(x)k

∞

≤ 1.077 × 10

−8

Using the three-term recurrence relation (or looking it up in a computer algebra

package), we ﬁnd that

(x) = 2

− 576x

+ 432x

− 120x

+ 9x.

Thus

p(x) = x −

−

− T

(x)/2

310 Approximation by Polynomials

has degree 7. This polynomial approximates sin(x) on [−1, 1] with error at most

3.6 × 10

−8

For comparison, the Taylor polynomial of degree 7 gives an error of about

2.73 × 10

−6

. Thus, p(x) is 75 times as accurate as the Taylor polynomial of the

same degree.

In practice, we want to do away with ad hoc methods and ﬁnd an algorithm

that yields reasonably good approximations quickly. We need the following inner

product for f, g ∈ C[−1, 1]:

hf, gi

−1

f(x)g(x)

√

1 − x

It is easy to verify that this is an inner product on C[−1, 1] (i.e., it is linear in both

variables, positive deﬁnite and symmetric). The crucial property we need is that

the Chebychev polynomials are orthogonal with respect to this inner product. The

constant 1/π makes the constant function 1 have norm 1, which is computationally

convenient.

10.7.5. LEMMA.

, T











0 if m 6= n

if m = n 6= 0

1 if m = n = 0

PROOF. Make the substitution cosθ = x in the integral, so that −sinθ dθ = dx,

whence dθ = −dx/

√

1 − x

. We have

, T

−1

(x)T

(x)

√

1 − x

cosnθ cosmθ dθ

2π

cos(m + n)θ + cos(m − n)θ dθ,

where again we have used the identity 2cosA cosB = cos(A + B) + cos(A −B).

There are three different integrals, depending on the values of m and n. If

m 6= n, then both m + n and m − n are not zero and the integral is

2π

sin(m + n)θ

m + n

sin(m − n)θ

m − n

= 0.

If m = n 6= 0, then m − n is zero and m + n is not, so the integral is

2π

sin(m + n)θ

m + n

+ x

Finally, if m = n = 0, then the integral is 1. ¥

10.7 Expansions Using Chebychev Polynomials 311

Now suppose for a moment that a function f ∈ C[−1, 1] can be expressed as

an inﬁnite sum of Chebychev polynomials. That is, there is a sequence of constants

)

∞

n=1

so that

f(x) =

∞

n=1

(x)

for all x ∈ [−1, 1]. Then, willfully ignoring the issue of convergence, we can write

hf, T

∞

n=1

, T

∞

n=1

, T

= a

, T

Solving for a

in the preceding equation and using the deﬁnition of the inner prod-

uct, we have a possible formula for the coefﬁcients:

= 2hf, T

−1

f(x)T

(x)

√

1 − x

for k ≥ 1

and

= hf, T

−1

f(x)

√

1 − x

10.7.6. DEFINITION. We deﬁne the Chebychev series for f in C[−1, 1] to be

∞

n=1

(x), where the sequence (a

) is given by the preceding formulas.

There are a host of questions about this series. For which x does this inﬁnite

series converge? Is the resulting function continuous? Does it equal f or not?

Under some conditions, the expansion does converge. The underlying reason

is a connection between Chebychev series and Fourier series, which we explore at

the end of Chapter 14. Rather than be too repetitive, we limit ourselves here to one

of the easier results. See Theorem 14.8.2 for a much better result that requires a

more subtle analysis.

10.7.7. THEOREM. If f ∈ C[−1, 1] has a continuous second derivative, then

the Chebychev series of f converges uniformly to f.

PROOF. We wish to obtain a good estimate on the size of the coefﬁcients a

for

k ≥ 1. Again make the change of variables x = cosθ; then

−1

f(x)T

(x)

√

1 − x

g(θ) cosnθ dθ,

312 Approximation by Polynomials

where g(θ) = f(cosθ). Using integration by parts,

g(θ)

sinnθ

−

(θ)

sinnθ

dθ

− g

(θ)

cosnθ

−

(θ)

cosnθ

dθ

Now g

(θ) = −f

(cosθ) sinθ vanishes at 0 and π, so the integral simpliﬁes to

−2

πn

(θ) cosnθ dθ.

Since f has a continuous (and thus bounded) second derivative, it follows that g

does also. If M = sup{|g

(θ)| : θ ∈ [0, π]}, then a

≤ 2M/n

. So, by the

Comparison Test,

∞

n=1

converges.

Since ka

∞

= a

, the Weierstrass M-test (8.4.7) shows that

∞

n=1

converges uniformly to some continuous function F ∈ C[−1, 1]. It remains only

to show that F = f.

Observe that for all n ≥ 1,

hf − F, 2T

= a

− lim

k→∞

j=0

(x), 2T

(x)

= a

− a

= 0.

Likewise, hf − F, T

= 0. Using the integral deﬁnition of the inner product, we

have

−1

f(x) − F (x)

√

1 − x

(x) dx = 0 for all n ≥ 0.

Since T

is a polynomial of degree n, a routine induction argument shows that

−1

f(x) − F (x)

√

1 − x

dx = 0 for all n ≥ 0,

and therefore

−1

(f(x) − F (x))

1 − x

dx =

−1

f(x) − F (x)

√

1 − x

− x

n+2

) dx = 0.

By Exercise 10.2.D, it follows that (f(x) −F (x))

√

1 − x

= 0 for all x ∈ [−1, 1].

Since f and F are continuous, we deduce that f(x) = F (x) on [−1, 1]. ¥