Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

Part B

Applications

CHAPTER 10

Approximation by Polynomials

This chapter introduces some of the essentials of approximation theory, in partic-

ular approximating functions by “nice” ones such as polynomials. In general, the

intention of approximation theory is to replace some complicated function with a

new function, one that is easier to work with, at the price of some (hopefully small)

difference between the two functions. The new function is called an approximation.

There are two crucial issues in using an approximation: ﬁrst, how much simpler is

the approximation? and second, how close is the approximation to the original

function? Deciding which approximation to use means looking at the trade-off

between these two issues.

Of course, the answers to these two questions depend on the exact meanings of

simpler and close, which vary according to the context. In this chapter, we study

approximations by polynomials, so here a simpler function means a polynomial.

Close usually refers to some norm. We focus on the uniform norm so that the

polynomial is close to the function everywhere on a given interval.

Approximations are closely tied to the notions of limit and convergence, as

a sequence of functions approximating a function f to greater and greater accu-

racy might be expected to converge to f in some sense. Different approximation

schemes correspond to different notions of convergence.

10.1. Taylor Series

The ﬁrst approximation taught in Calculus and the most often used approxima-

tion is the tangent line approximation: If f : R → R is differentiable at a ∈ R,

then for x near a, we have

f(x) ≈ f(a) + f

(a)(x − a).

However, you should learn early that an approximation is only as good as the

error estimate that can be veriﬁed. Unless we can estimate the error, the difference

between f(x) and its approximation f (a) + f

(a)(x − a), it is impossible to say

whether or not the approximation is worth the trouble. For example, why not just

approximate f(x) with the constant f(a), since x is “near” a and f is continuous?

275

276 Approximation by Polynomials

We start with the error estimate for the constant approximation f (a). This error

estimate comes from the Mean Value Theorem (Theorem 6.2.4), which gives us the

estimate |f(x)−f(a)| = |f

(c)(x−a)| ≤ C|x−a|, where c is some point between

a and x and C = sup{|f

(c)| : c between x and a}. When C is ﬁnite, we obtain

a useful error estimate for this constant approximation. Notice that this estimate

does not require us to ﬁnd f(x) exactly. If we could easily ﬁnd f(x), we wouldn’t

bother with the approximation.

A more sophisticated use of the Mean Value Theorem shows that the tangent

line has an error of the form M(x − a)

for a constant M that depends on f

For x very close to a, this is a considerable improvement on C|x − a|. See Exer-

cise 10.1.B. Very similar calculations were done in Example 6.2.6.

In this section, we generalize these two approximations and their error esti-

mates to take account of higher derivatives—in other words, we generalize the

Mean Value Theorem. As this method requires many derivatives, and because it

only uses information at one point, it will not be an ideal method for uniform ap-

proximation over an interval. Nevertheless, it works very well in certain instances

of great importance, and it is easier to understand than the alternative methods.

Later in this chapter we will explore other methods for ﬁnding polynomial approx-

imants which are uniformly close over an interval.

The role of the tangent line to f is replaced by a polynomial P

(x) of degree

at most n that has the same derivatives at a as f up to the nth degree. This is all

that the parameters of a polynomial of degree at most n permit.

10.1.1. DEFINITION. If f has n derivatives at a point a ∈ [A, B], the Taylor

polynomial of order n for f at a is

(x) = f (a) + f

(a)(x − a) +

(a)

(x − a)

+ ··· +

(n)

(a)

(x − a)

k=0

(k)

(a)

(x − a)

10.1.2. LEMMA. Let f(x) belong to C

[A, B] (i.e., f has n continuous deriv-

atives), and let a ∈ [A, B]. The Taylor polynomial P

(x) of order n for f at a

is the unique polynomial p(x) of degree at most n such that p

(k)

(a) = f

(k)

(a) for

0 ≤ k ≤ n.

PROOF. Every polynomial of degree at most n has the form p(x) =

j=0

(x−a)

We may differentiate this k times to obtain

(k)

(x) =

j=k

j(j − 1) . . . (j + 1 −k)(x − a)

j−k

Substituting x = a yields p

(k)

(a) = k!a

. Therefore, we must choose the coefﬁ-

cients a

= f

(k)

(a)/k!, which yields the Taylor polynomial P

(x). ¥

10.1 Taylor Series 277

The preceding simple lemma established that the Taylor polynomial is the ap-

propriate analogue of the tangent line for higher order polynomials. The hard work,

and indeed the total content of this approximation, comes from the error estimate.

In this case, the estimate is only good for points sufﬁciently close to a when there

is reasonable control on the size of the (n + 1)st derivative. The case n = 0 is a

direct consequence of the Mean Value Theorem.

10.1.3. TAYLOR’S THEOREM.

Let f(x) belong to C

[A, B], and furthermore assume that f

(n+1)

is deﬁned and

(n+1)

(x)| ≤ M for x ∈ [A, B]. Let a ∈ [A, B], and let P

(x) be the Taylor poly-

nomial of order n for f at a. Then for each x ∈ [A, B], the error of approximation

(x) = f (x) − P

(x) satisﬁes

(x)| ≤

M|x − a|

n+1

(n + 1)!

PROOF. Notice that for 0 ≤ k ≤ n,

(k)

(a) = f

(k)

(a) − P

(k)

(a) = 0,

and because P

is a polynomial of degree at most n,

(n+1)

(x) = f

(n+1)

(x) − P

(n+1)

(x) = f

(n+1)

(x).

For the base case, applying the Mean Value Theorem to R

(n)

gives

(n)

(x)| = |R

(n)

(x) − R

(n)

(a)| ≤ M |x − a|

Suppose that for some k with 0 ≤ k < n we have shown that

(n−k)

(x)| ≤

M|x − a|

k+1

(k + 1)!

Then we integrate to obtain

(n−k−1)

(x)| =

(n−k−1)

(a) +

(n−k)

(t) dt

≤

0 +

M|t − a|

k+1

(k + 1)!

M|x − a|

k+2

(k + 2)!

We established the formula for k = 0, and have now completed the induction

step. Eventually we obtain the desired formula where k = n,

(x)| ≤

M|x − a|

n+1

(n + 1)!

When f is C

∞

, the Taylor series of f about a is

∞

k=0

(k)

(a)

(x − a)

. This is

a power series, and so we must watch out for problems with convergence.

278 Approximation by Polynomials

10.1.4. EXAMPLE. Consider the function f(x) = e

. This function has the

very nice property that f

= f. Thus f

(n)

(x) = e

for all n ≥ 0. So expanding

around a = 0, we obtain Taylor polynomials P

(x) =

k=0

. We readily see that

(n+1)

(t)| = e

≤ max{1, e

} if t lies between 0 and x. Thus Taylor’s Theorem

for the interval [0, x] (or [x, 0]) tells that the error has the form

−

k=0

≤ max{1, e

}

|x|

n+1

(n + 1)!

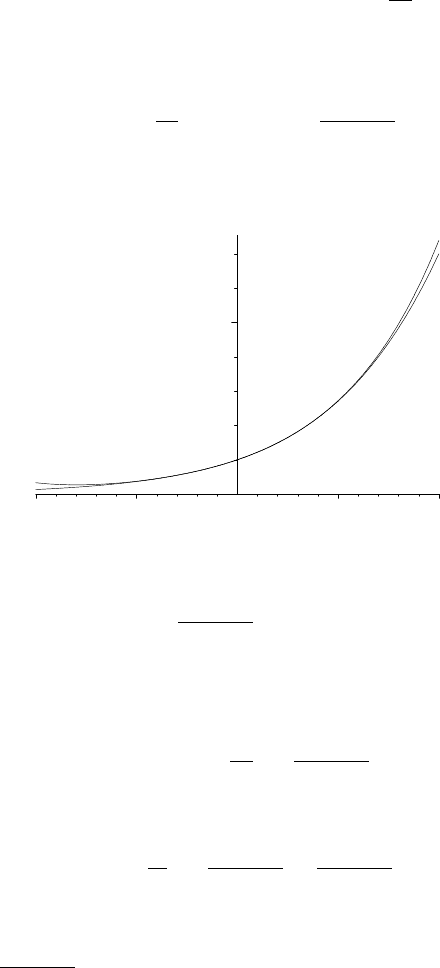
Even for low values of n, P

(x) appears quite close to e

around the origin; see

Figure 10.1.

–2

–1 1

FIGURE 10.1. e

and P

(x) on [−2, 2].

The ratio test shows that lim

n→∞

|x|

n+1

(n + 1)!

= 0. Thus the Taylor series converges

to e

for every x ∈ R. Moreover, this series converges uniformly on any interval

[−A, A]. To see this, notice that the error estimate at any point x ∈ [−A, A] is

greatest for x = A. Hence

sup

|x|≤A

−

k=0

≤

n+1

(n + 1)!

To compute e, we could use this formula to compute

e −

k=0

≤

(n + 1)!

≤

(n + 1)!

So to obtain e to 10 decimal places, we need

(n + 1)!

< 5(10)

−11

or (n + 1)! > 6(10)

A calculation shows that we need n = 13.

This is not too bad, yet we can signiﬁcantly increase the rate of convergence by

using a smaller value of x. For example, suppose that we use x = 1/16 to compute

10.1 Taylor Series 279

1/16

. We can then square this number 4 times to obtain e. If we use just the ﬁrst

10 terms, we have

1/16

−

k=0

(16)

≤

1/16

(16)

(11)!

< 1.6(10)

−21

Then we take the number a =

k=0

(16)

and square it 4 times to obtain a

as an approximation to e. Since we know that e

1/16

− ε < a < e

1/16

, where

ε = 1.6(10)

−21

, we have

e > a

> (e

1/16

− ε)

> e − 16e

15/16

ε > e − 7(10)

−20

So roughly the same number of calculations yields almost double the number of

digits of accuracy.

Consider the power series

∞

n=0

. The ratio test shows that

lim

n→∞

|x|

n+1

/(n + 1)!

|x|

/n!

= lim

n→∞

|x|

n + 1

= 0

for every real x. Thus this power series has an inﬁnite radius of convergence.

Moreover, as we showed previously, this series converges to the function e

; and

this convergence is uniform on each bounded interval.

A similar situation occurs for sinx and cos x.

Many functions in common use are C

∞

, meaning that they have continuous

derivatives of all orders. For such functions, the Taylor polynomials of all orders

are deﬁned. Thus it is natural to consider the convergence of the Taylor series of

f around x = a. Recall from Section 8.5 that every power series has a radius of

convergence. In the previous example, the best possible result occurred—the power

series of e

had an inﬁnite radius of convergence, and the limit of the series was

the function itself. Unfortunately, things are not always so good.

10.1.5. EXAMPLE. Consider the function f(x) =

1 + x

. The formulas for

the derivatives are a bit complicated, so we use a trick. Consider the geometric

series

k=0

(−x

)

= 1 − x

+ x

+ ··· + (−x

)

1 − (−x

)

n+1

1 + x

If we set P

(x) =

k=0

(−x

)

, we have the estimate

1 + x

− P

(x)

2n+2

1 + x

280 Approximation by Polynomials

Thus

lim

x→0

|f(x) − P

(x)|

2n+1

= lim

x→0

|x|

1 + x

= 0.

By Exercise 10.1.C, it follows that this is indeed the Taylor polynomial for f not

only of order 2n, but also of order 2n + 1.

So the Taylor series is

∞

k=0

(−x

)

. The radius of convergence is readily seen to

be 1, since for |x| ≥ 1 the terms to do not go to 0; while for |x| < 1, the geometric

series does converge. Moreover, the limit is our function f (x). In Example 8.4.8,

we saw that convergence is uniform on each set [−r, r], for r < 1.

We conclude that even if the function is deﬁned and C

∞

on the whole real line,

the Taylor series may only converge on a ﬁnite interval.

10.1.6. EXAMPLE. In the last example, we showed that for any r < 1, the

series for 1/(1 + x

) converges uniformly on [−r, r]. Thus we may integrate this

series term by term by Theorem 8.3.1. For |x| = r < 1,

tan

−1

(x) =

1 + t

dt =

lim

n→∞

k=0

(−t

)

= lim

n→∞

k=0

(−t

)

= lim

n→∞

k=0

(−1)

2k + 1

2k+1

∞

k=0

(−1)

2k + 1

2k+1

This is the Taylor series for tan

−1

(x). It also has radius of convergence 1 and

converges uniformly on [−r, r] for any r < 1. This series also converges at x = ±1

by the alternating series test.

The next thing to notice is that this series does converge to tan

−1

(x) uniformly

on [−1, 1]. To see this, we use the alternating series test at each point x ∈ [−1, 1].

We have P

(x) =

n−1

k=0

(−1)

2k + 1

2k+1

. This is a sequence of polynomials of degree

2n−1 that converges to tan

−1

(x) at each point in [−1, 1]. The corresponding series

is alternating in sign with terms of modulus |x|

2k+1

/(2k + 1) tending monotonely

to 0. Thus the error is no greater than the modulus of the next term.

tan

−1

(x) − P

(x)

|x|

2n+1

2n + 1

≤

2n + 1

Therefore,

sup

|x|≤1

tan

−1

(x) − P

(x)

≤

2n + 1

So P

converges uniformly to tan

−1

(x) on [−1, 1].

10.1 Taylor Series 281

However, this sequence converges very slowly. Indeed, by the triangle inequal-

ity for the max norm in C[−1, 1],

2n + 1

= kP

− P

2n+2

∞

≤ kP

− fk

∞

+ kf − P

2n+2

∞

So max

− f k

∞

, kf − P

2n+2

∞

≥

4n + 2

, which is a rather slow rate of

convergence.

On the other hand, this estimate shows that the error on [−r, r] is no more

than r

2n+1

/(2n + 1), which goes to zero quite quickly as n → ∞, if r is small.

So Taylor series can sometimes be a good approximation in a limited range. See

Exercise 10.1.E for a method of rapidly computing π using these polynomials.

Taylor polynomials can be used to evaluate limits. Perhaps you have seen

L’H

opital’s Rule in calculus. Taylor polynomials are equally powerful and provide

a better method because their application follows naturally from an understanding

of approximation rather than blindly following a rule.

For convenience, we introduce the big O notation (pronounced big oh). A

function f(x) is O(g) near x = a if there is a constant M and a δ > 0 so that

|f(x)| ≤ M|g(x)| for all 0 < |x − a| < δ.

For example, Taylor’s Theorem concludes that |f(x) − P

(x)| = O

(x − a)

n+1

The advantage of big O notation is that it allows you to forget about the precise

constants involved in the inequality. The reader can check that the following simple

arithmetic rules are valid.

(1) O(f) ± O(g) = O(max{f, g})

In particular, O

(x − a)

± O

(x − a)

= O

(x − a)

min{m,n}

(2) O(f)O(g) = O(fg)

In particular, O

(x − a)

= O

(x − a)

m+n

(3)

(x − a)

= O

(x − a)

m−n

10.1.7. EXAMPLE. Consider lim

x→0

+ e

−x

− 2

. We saw in Example 10.1.4

that e

= 1 + x +

+ O(x

) near x = 0. Hence

+ e

−x

− 2

1 + x +

+ O(x

) + 1 −x +

+ O(x

) − 2

+ O(x

)

= 1 + O(x).

Hence lim

x→0

+ e

−x

− 2

= lim

x→0

1 + O(x) = 1.

282 Approximation by Polynomials

10.1.8. EXAMPLE. Now consider a more complicated limit lim

x→0

cot

x −

We will use the Taylor polynomials for sin and cos:

sinx = x − x

/6 + O(x

) and cosx = 1 −x

/2 + O(x

Then

cot

x −

cos

sin

−

1 − x

/2 + O(x

)

1 − x

/6 + O(x

)

−

1 − x

+ O(x

)

−

1 − x

/3 + O(x

)

1 − x

/3 + O(x

)

−2/3 + O(x

)

1 − x

/3 + O(x

)

Hence

lim

x→0

cot

x −

= lim

x→0

−2/3 + O(x

)

1 − x

/3 + O(x

)

= −

10.1.9. EXAMPLE. Even if f has derivatives of all orders that we can evaluate

accurately and the Taylor series converges uniformly, the Taylor polynomials may

not converge to the right function! The classic example of this is the function

f(x) =

(

−1/x

if x 6= 0

0 if x = 0.

Figure 10.2 shows just how ﬂat this function is near zero.

0.5

–4 4

FIGURE 10.2. The graph of e

−1/x

We will show that f is C

∞

on all of R and f

(n)

(0) = 0 for all n. We claim that

there is a polynomial q

(x) of degree at most 2n so that

(n)

(x) =

(x)

−1/x

for x 6= 0.