Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond
Подождите немного. Документ загружается.


9.4 Glassy aging dynamics 471
the solution (9.3.71) requires that α = δa and g
i
(x) ∼ B
i
x
−ia
for x 1, where the
variable x is defined as τ = t −t
= xt
δ
. On the other hand, for the aging regime x 1,
on comparing with (9.3.72) we obtain g
i
(x) ∼ x
i
. In this case the exponent δ for the
crossover time scale is related to the exponent κ of the aging behavior (9.3.74) through
the relation δ + α = μ (Andreanov and Lefèvre, 2006). The corresponding relation to the
power-law exponent a of the FDT regime is δ(1 +a) = μ. In the final relaxation process
over the time scale of τ ∼ O(t), the behavior of the correlation function is controlled by
φ(λ), always decaying to zero since h(t) is a monotonically ascending function of time.
Thus, for any time t
, if one waits long enough, there is always a t for which the correlation
function decays to zero. This is termed quasi-ergodic behavior.
The nonequilibrium dynamics of the mean-field p-spin model discussed so far in this
section has not been extended to deal with the structural-glass problem involving multiple
slow variables. However, in a somewhat simplified approach, these mean-field equations
for the time evolutions of the correlation and response functions have been applied to study
nonequilibrium dynamics in some cases, e.g., in theproblem of nonlinear rheology (Berthier
et al., 2000) and for the dynamics of hetero-polymers (Pitard and Shakhnovich, 2001).
9.4 Glassy aging dynamics
The effective temperature T
eff
for the nonequilibrium state defined above refers to a partic-
ular mode O of the system. However, as the system equilibrates the effective temperatures
linked to the different such observables should all approach the common bath tempera-
ture. The process of thermalization in the dynamics of the nonequilibrium state can be
understood using the equations of motion of the mean-field model discussed above.
9.4.1 Thermalization
To generalize the above formulation, let us consider here a set of slow modes labeled as
a, b, c,...for which we write down the dynamical equations for the correlation C =(C
ab
)
and the response function R =(R
ab
). This is done in the same manner as was done before
for the single-spin model (see eqns. (9.3.14) and (9.3.15)),
∂
∂t
C
ab
(t, t
) =−
c
z
ac
(t)C
cb
(t, t
) + 2R
ab
(t
, t)
+
c
t
0
dt
ac
(t, t
)R
cb
(t
, t
)
+
t
0
dt
c
ac
(t, t
)C
cb
(t
, t
), (9.4.1)
∂
∂t
R
ab
(t, t
) =−
c
z
ac
(t)R
cb
(t, t
) + δ(t − t
)δ
ab
+
t
t
dt
c
ac
(t, t
)R
cb
(t
, t
). (9.4.2)

472 The nonequilibrium dynamics
For the sake of definiteness we take t > t
. The time-ordered property of the response func-
tion, i.e., R
ab
(t, t
) = 0fort < t
due to causality, has been used in writing eqns. (9.4.1)
and (9.4.2). As before, we have two qualitatively different types of regimes characterizing
the dynamics.
(a) The quasi-equilibrium or FDT regime for t, t
→∞and t − t
finite. In this case TTI
holds and we have the usual FDT relation
R
ab
(t − t
) =
1
T
∂
∂t
C
ab
(t − t
), (9.4.3)
where we have used the units in which k
B
=1. R
ab
(t, t
) vanishes for t
> t due to
causality. The memory functions of the corresponding TTI quantities are related,
ab
(t − t
) =
1
T
∂
∂t
ab
(t − t
). (9.4.4)
In this regime eqns. (9.4.1) and (9.4.2) for the correlation functions and response
functions reduce to a single equation of the equilibrium MCT.
(b) The aging regime in which t, t
→∞such that (t − t
)/t ∼ O(1). The corresponding
correlation and response functions obey the relations
˜
C
ab
(t, t
) =
˜
C
ab
h
ab
(t
)
h
ab
(t)
, (9.4.5)
˜
R
ab
(t − t
) =
m
ab
T
∂
∂t
˜
C
ab
(t − t
), (9.4.6)
where the h
ab
(t) are monotonically ascending functions of time and the m
ab
are con-
stants. The equations for the time evolution of the correlation and response functions
reduce to a closed set with a suitable ansatz for the different effective temperatures.
Cugliandolo et al. (1997b) proposed two types of scenarios concerning the effective
temperatures for the nonequilibrium dynamics. Each scheme represents a correspond-
ing characteristic thermalization process.
I. In the quasi-equilibrium or FDT regime the effective temperatures corresponding to
two different observables O
1
and O
2
are equal to each other and equal to the temper-
ature of the bath. Here the FDT is satisfied and we have for the memory functions, to
which the corresponding TTI quantities are related,
ab
(t − t
) =
1
T
∂
∂t
ab
(t − t
). (9.4.7)
In the aging regime the effective temperatures corresponding to O
1
and O
2
are equal
to each other but not necessarily equal to that of the heat bath,
˜
R
11
(t − t
) =
m
11
T
∂
∂t
C
11
(t − t
), (9.4.8)
˜
R
22
(t − t
) =
m
22
T
∂
∂t
C
22
(t − t
), (9.4.9)

9.4 Glassy aging dynamics 473
with m
11
= m
22
. The behavior of effective temperature in the aging regime being
independent of the observable is termed thermalized aging. In this situation O
1
and O
2
are strongly coupled, and for the off-diagonal elements of the correlation and response
functions we have
˜
R
12
(t − t
) =
¯m
T
∂
∂t
˜
C
12
(t − t
), (9.4.10)
where ¯m > 0 and is of the same order as the similar quantities appearing in the cor-
responding relations for self-response functions R
11
, R
22
, etc. Thus m
11
= m
22
=
m
12
= m
21
≡¯m. The corresponding memory functions in the aging regime satisfy
˜
ab
(t − t
) =
¯m
T
∂
∂t
ab
(t − t
), ∀a, b. (9.4.11)
The scaling functions h
ab
(t) for the aging dynamics are the same for all a and b in this
case, such that
˜
C
ab
(t, t
) =
˜
C
ab
[h(t
)/ h(t)].
II. In the quasi-equilibrium or FDT regime the effective temperatures corresponding to
two different observables O
1
and O
2
are equal to each other and equal to the temper-
ature of the bath. This is the same as in scheme I. However, in the aging regime the
effective temperatures are not equal to each other and neither is equal to that of the heat
bath. Thus m
11
= m
22
. Therefore the effective temperature in the aging regime is dif-
ferent for different observables. In this situation O
1
and O
2
are effectively decoupled
and hence for the off-diagonal elements of the correlation and response functions we
have
˜
R
12
(t − t
) =
m
12
T
∂
∂t
˜
C
12
(t − t
), (9.4.12)
where m
12
, m
21
→ 0. This is termed unthermalized aging behavior.
9.4.2 Aging dynamics: experiments
In deeply supercooled liquids the relaxation is typically nonexponential, a behavior that has
been linked in the recent literature to the heterogeneous nature of the dynamics of the liquid
particles. Spatially extended and structurally heterogeneous regions appear in the nonequi-
librium state and the dynamic properties of the undercooled liquid change with its aging.
Lehny and Nagel (1998) studied the dielectric response of a typical glass-forming mate-
rial, glycerol (fragility index m =53), following a quench from a high temperature to one
below the glass-transition temperature T
g
. Those authors studied the dielectric response of
the liquid for different values of the aging time t
age
, which is measured conveniently from
the instant of quenching. The dielectric susceptibility
(ν,t
age
) =
(ν, t
age
) + i
(ν, t
age
) (9.4.13)
is a function of the frequency as well as the aging time. In the equilibrated system, for
large enough t
age
the spectrum is time-independent and the imaginary part
(ν) displays
a broad peak whose position ν
p
decreases with temperature following a Vogel–Fulcher
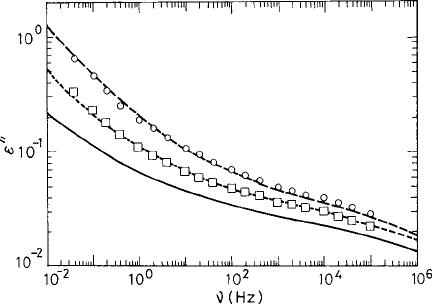
474 The nonequilibrium dynamics
Fig. 9.10 Plots of
(ν, t
age
) of glycerol vs. frequency ν following a quench from 206.2 K to
177.6 K corresponding to two different aging times: t
age
= 200 s (circles) and t
age
= 2 × 10
4
s
(squares). The lines are equilibrium spectra at three temperatures: 177.6 K (solid), 180.1 K (dotted),
and 182.5 K (dot–dashed). The spectra after 200 s and 2 × 10
4
s for the nonequilibrium liquid fol-
lowing this quench closely approximate the equilibrium spectra at 182.5 K and 180.1 K, respectively.
Reproduced from Lehny and Nagel (1997).
c
American Physical Society.
law. At T = T
g
= 185 K the peak frequency for glycerol is ν
p
≈ 10
−3
Hz. The aging
experiment for the nonequilibrium state was done for frequencies above this value. For
quenches to not far below T
g
the
(ν, t
age
) vs. ν curves for different values of t
age
mimic
the equilibrium response
eq
(ν) vs. ν curve at a higher temperature. This behavior is dis-
played in Fig. 9.10 for a quench from T = 206.2Kto T = 177.6 K. The lower the value
of t
age
, the higher the temperature for the corresponding equilibrium curve. This important
observation indicates that, at least for quenches close to the glass-transition temperature
T
g
, the spectral shape of the dielectric susceptibility changes similarly with time during the
aging process. The identification of the aging system with the corresponding equilibrium
one provides us with a way of associating a temperature with the out-of-equilibrium glassy
state. This is similar to the phenomenological fictive temperature T
fic
discussed above. For
temperatures far below T
g
such a mapping does not follow, however.
Modified Kohlrausch–William–Watts (MKWW) relaxation
Let us consider another important aspect of the aging behavior, i.e., the manner in which
a typical response function for the nonequilibrium state (in this case that of the dielec-
tric response) changes with the aging time t
age
. The dielectric-loss response function
for glycerol quenched to temperature 179 K (T
g
= 185 K ) fits well to the Kohlrausch–
Williams–Watts (KWW) form over the frequency range ν =1Hz −10
5
Hz. The fitted
form is
t
age
=
(
st
−
eq
)
exp
!
−(t
age
/τ
age
)
β
age
"
+
eq
. (9.4.14)

9.4 Glassy aging dynamics 475
The subscripts “st” and “eq” in the above formula respectively refer to the initial (t
age
→ 0)
and long-time (t
age
→∞) limiting values of
.Both
st
and
eq
are obtained as corre-
sponding parameter values to obtain the best fit of the experimental data to the above
form. The relaxation time τ
age
and the stretching exponent β
age
are also treated as free fit
parameters. Generally all these parameters for data fitting are dependent on the frequency
ν for the corresponding response function. The τ
age
or β
age
obtained in this procedure,
however, do not agree with the corresponding equilibrium (extrapolated) parameter values.
τ
α
and β
α
.
1
The stretching exponent β
age
is usually much smaller than β
α
. For example,
in the case of glycerol β
age
≈ 0.29 while the extrapolated β
α
= 0.55. An important
observation in this regard was made by Lunkenheimer et al. (2005) who demonstrated that
using a modified KWW (MKWW) fitting function the aging-time dependence of the above
dielectric-response-function data for the different frequencies (ν) can be simultaneously
fitted very well with frequency-independent τ
age
and β
age
. The relaxation time τ
age
in the
stretched exponential function is itself dependent on the aging time t
age
(Zotev et al., 2003;
Bissig et al., 2003).
t
age
=
(
st
−
eq
)
exp
−
t
age
/τ
age
(t
age
)
β
age
+
eq
. (9.4.15)
The aging-time dependence of τ
age
(t
age
) can be obtained in two different ways, implying
two very different mechanisms for the aging process in the supercooled liquid. Let us
consider both.
I. Lunkenheimer et al. (2005) defined the dependence of the relaxation time τ
age
on t
age
in the MKWW in terms of a corresponding “time-dependent” frequency ν
age
intro-
duced as
τ(t
age
) =
1
2πν
age
(t
age
)
. (9.4.16)
The aging-time dependence of ν
age
is chosen in the parametric form
ν
age
t
age
=
ν
st
− ν
eq
exp
−
2πν(t
age
)t
age
β
age
+ ν
eq
. (9.4.17)
In the above definition τ
age
→ 1/(2πν
st
) and 1/(2πν
eq
) as t
age
→ 0 and ∞, respec-
tively. An almost-perfect fit for the dielectric data over the whole frequency range
is obtained with the above choice of the time dependence for the relaxation time.
β
age
and β
age
are now the same for the response-function data at different frequen-
cies ν = 1 −10
5
Hz. This scaling of the response function is shown in Fig. 9.11.An
important feature of the above fitting procedure is that the best-fit values for the stretch-
ing exponent β
age
for a number of glass-forming systems are found to be the same as
those of the corresponding α-relaxation β
α
. Furthermore, the best-fit value obtained
for ν
eq
in (9.4.17) corresponds to a time τ
eq
= 1/(2πν
eq
), which agrees well with the
corresponding α-relaxation time τ
α
(for a given substance) obtained by extrapolation
1
At the sub T
g
temperature, the equilibrium counterpart of τ
age
, denoted τ
α
, is obtained by extrapolating the results of the
corresponding equilibrium
α-relaxation times at T > T
g
.
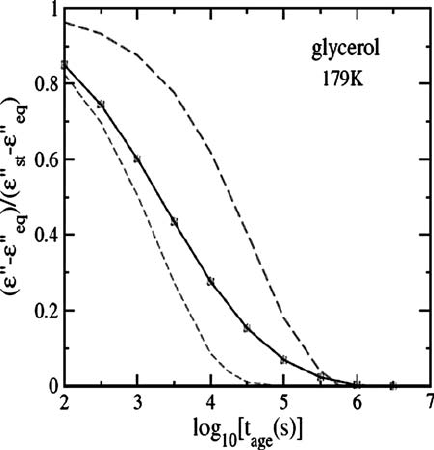
476 The nonequilibrium dynamics
Fig. 9.11 Scaling of the dielectric-response function of glycerol at 179 K for different frequencies.
The fits are obtained with τ
age
(t
age
) in the modified KWW ansatz using two schemes (see the text):
(i) eqns. (9.4.18) and (9.4.19) (the solid line) and (ii) eqns. (9.4.15)–(9.4.17) (the dashed line almost
coincident with the solid line). Also shown are the curves obtained with the normal KWW form, in
both of which (i) the stretching exponent is fixed at β
α
, and (ii) the relaxation time τ
age
is respectively
equal to τ
st
(short-dashed line) and τ
eq
(long-dashed line). From Lunkenheimer et al. (2005) and Sen
Gupta and Das (2007).
c
American Physical Society.
from higher temperatures (T > T
g
) to sub-T
g
regions. In Fig. 9.12 the variation τ
α
with
inverse temperature 1/T is shown for a number of glass formers. The same figure also
displays (with stars) the corresponding value of τ
eq
= 1/(2πν
eq
) obtained from the
best-fit value in the above MKWW fitting scheme. It lies on the extrapolated curve of
the α-relaxation times in the sub-T
g
regime. The equilibrium α-relaxation thus seems
to be closely related to the aging process. The stretching exponents being the same in
both cases (β
age
= β
α
) possibly implies that the stretching of the relaxation remains
unaffected by aging and hence conforms to the validity of the time–temperature super-
position during the aging process. Thus, if the aging behavior is indeed due to the
structural rearrangements of heterogeneous regions, we expect that τ
age
and β
age
are
primarily controlled by the α-relaxation mechanism.
II. As an alternative to the above scheme, an equally good fit to the aging data is obtained
(Sen Gupta and Das, 2007) by choosing the t
age
dependence of the relaxation time τ
age
in the MKWW function in a more natural manner
τ
age
(t
age
) =
(
τ
st
− τ
fn
)
F(t
age
) + τ
fn
. (9.4.18)
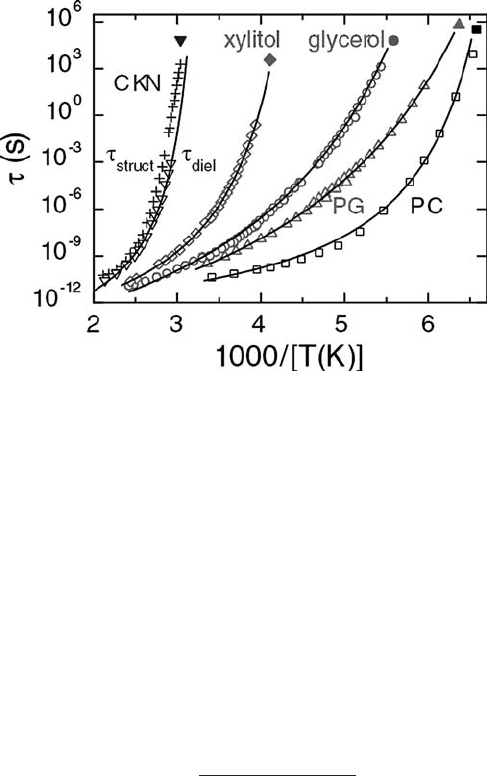
9.4 Glassy aging dynamics 477
Fig. 9.12 Plots of α-relaxation times τ
α
from measurements of equilibrium dielectric properties for
different glass formers (open symbols). The lines are fit with the Vogel–Fulcher–Tammann law. For
CKN the structural-relaxation times from mechanical spectroscopy are also displayed (+signs).The
closed symbols show the best-fit values obtained from the fitting of the aging-time dependence of the
nonequilibrium data using eqns. (9.4.15)–(9.4.17). From Lunkenheimer et al. (2005).
c
American
Physical Society.
The function F (t) reduces to the value 1 or 0, for t → 0 and ∞, respectively, so that the
relaxation time τ
age
attains the asymptotic values τ
st
and τ
fn
respectively in the above
two limits. A perfect fit is obtained for all the
(t
age
) data at different frequencies
using eq. (9.4.14) with τ
age
(t
age
) being determined with the ansatz (9.4.18). Among the
different choices of the function f (t) in (9.4.18) the best-quality fit is obtained with
(Sen Gupta and Das, 2007)
f (t) =
2
1 + exp{2t/τ
age
(t)}
β
age
(9.4.19)
The fittings over the whole frequency range of the dielectric data are shown in Fig. 9.11,
in which all the data scale into a single master curve. This fitting scheme suggests the
following alternative scenario for explaining the dielectric-relaxation data as follows:
The aging process involves two basic steps. In the first stage, the aging data fits to
the MKWW form with a time-dependent relaxation time τ
age
. The time dependence of
τ
age
(t
age
) (given by eqn. (9.4.18)) is somewhat more natural than that of Lunkenheimer
et al.(givenbyeqn. 9.4.17). As t
age
reaches a characteristic time scale τ
fn
the data can
now be described in this second stage with a simple KWW form having a constant
relaxation time comparable to τ
fn
. This holds simultaneously for relaxation data for
the response functions at different frequencies (ν). The aging-time dependence of the
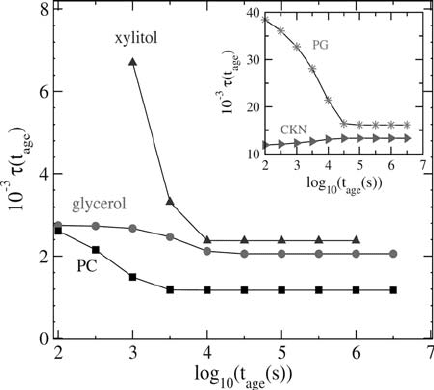
478 The nonequilibrium dynamics
Fig. 9.13 The MKWW relaxation time τ
age
(t
age
) vs. t
age
as obtained by fitting the dielectric-
relaxation data using the scheme given by eqn. (9.4.18) for various glass-forming materials. From
Sen Gupta and Das (2007).
c
American Physical Society.
relaxation time τ
age
is shown in Fig. 9.13 for various glass-forming materials. How-
ever, unlike the first fitting scheme, the limiting value of τ
fn
obtained here is not the
same as τ
α
discussed above. The stretching exponent is also very different from that
of the α-relaxation. This might equally well be indicative of a different mechanism
controlling the nonequilibrium dynamics apart from the equilibrium α-relaxation.

Appendix to Chapter 9
A9.1 The energy of the oscillator
We present here the calculation of the potential energy of the oscillator being driven by
eqn. (9.2.11). The oscillator variable x(t) is coupled to the observable O.Tosolvethe
inhomogeneous partial differential equation we use the following definition in terms of a
corresponding Green function G:
x(t) = ε
t
0
dt
G(t, t
)
˜
O(t
). (A9.1.1)
The Laplace transform of the Green function G(t, t
) is then obtained as
G(ω, t) =
1
−ω
2
+ ω
2
0
−
2
χ(ω,t)
. (A9.1.2)
In eqn. (A9.1.2) we have used the following definitions:
G(ω, t) =
t
0
dt
G(t, t
)e
−ω(t−t
)
, (A9.1.3)
χ(ω,t) =
t
0
dt
R
O
(t, t
)e
−ω(t−t
)
. (A9.1.4)
In order to take the inverse transform of (A9.1.2) one must find the poles of the denominator
on the RHS. Assuming that the coupling is weak enough (small ε), we consider the poles
in the vicinity of ω =±ω
0
in the following form:
ω ≈±ω
0
1 −
i
ω
0
τ
c
(t)
, (A9.1.5)
where the characteristic time τ
c
(t) for the damped oscillator is given by
τ
c
(t) =
2ω
0
ε
2
χ
(ω
0
, t)
. (A9.1.6)
Now, evaluating the contour integral in terms of the residue at the relevant pole, we obtain
for the Green function in real time
G(t, t
) = exp
−
t − t
τ
c
(t)
sin[ω
0
(t − t
)]θ(t − t
). (A9.1.7)
479

480 Appendix to Chapter 9
Now let us consider the mean-square displacement x
2
(t) of the oscillator (t ω
−1
0
) mea-
sured in a short interval at time t . Using the definition (A9.1.1), we now obtain for the
average of the square of the displacement
+
x
2
(t)
,
= ε
2
t
0
dt
t
0
dt
G(t, t
)G(t, t
)
˜
O(t
)
˜
O(t
). (A9.1.8)
On making changes of variables τ = t − t
and τ
= t − t
, we obtain
x
2
(t)=ε
2
t
0
dτ
t
0
dτ
G(t, t − τ)G(t, t − τ
)C
O
(t − τ,t − τ
). (A9.1.9)
Since causality requires that G(t, t
) = 0fort
> t, we can extend the lower limits of τ
and τ
to −∞. Also, since G(t, t
) decays exponentially with t − t
for large t, we can
extend the upper limits for τ and τ
to +∞. With these approximations we obtain
x
2
(t)=ε
2
+∞
−∞
dτ G(t, t − τ)
+∞
−∞
dτ
G(t, t − τ
)
×
+∞
−∞
dω
2π
C
O
(ω, t − τ)e
iω(τ−τ
)
. (A9.1.10)
The exponential decay of the Green function implies that the major contribution to the
above integral comes from the small-τ part and hence C
O
(ω, t −τ)in (A9.1.10) is replaced
by C
O
(ω, t), to obtain
x
2
(t)=ε
2
+∞
−∞
dω
2π
G(ω, t)G(−ω, t)C
O
(ω, t)
=
+∞
−∞
dω
2π
C
O
(ω, t)
χ
(ω, t) − χ
(−ω, t)
1
D
−
−
1
D
+
, (A9.1.11)
where we have used the definitions D
±
= ω
2
− ω
2
0
+ ε
2
χ
(±ω, t). The integral on the
RHS of the above expression for x
2
is computed by the method of residues. The poles
are obtained from the zeros of D
±
which appear in the denominators of the two terms
within square brackets on the RHS of (A9.1.11). The only singularities which contribute
to the integral are obtained by closing the latter on the upper half-plane. They lie in the
vicinity of
ω =±ω
0
+i ε
2
χ
(ω
0
, t)
2ω
0
. (A9.1.12)
Using the fact that the imaginary part χ
(ω) is an odd function of ω, we obtain from the
above the average of the square of the displacement x(t) to leading order in ε as
x
2
(t)=
C
O
(ω
0
, t)
ω
0
χ
(ω
0
, t)
,
(A9.1.13)
