Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

10.3 Self-generated disorder 501

Computation of the effective potential G

(q,β)

In order to compute the average (over the frozen conﬁgurations y)ofthelnZ

we use the

replica technique from spin-glass theory (Mézard et al., 1987). This is based on the identity

ln Z = lim

n→0

− 1

, (10.3.9)

where the overbar indicates the average of the corresponding quantity. On writing

as a

product of n identical replicas we obtain

=−k



−β H(x

)

Z(β)



···



exp



−β





α=1

H(x

) − γ



α=1

q(x

, y

)



. (10.3.10)

We have denoted above y ≡ x

. Evaluation of the RHS of eqn. (10.3.10) involves comput-

ing thermodynamic properties of an (n + 1)-component mixture in the n →0 limit. Note

that the replica denoted by x

is nonsymmetric with respect to the rest of the n replicas

denoted by {x

} for r =1,...,n. In the ﬁnal limit, unlike in the typical spin-glass prob-

lem, in the present case the number of replicas tends to one, not zero. Similar situations

occur in applying the replica trick to liquids (Stell, 1963; Goldbart et al., 1996) in which

the disorder is external or quenched, rather than being self-generated disorder as in the

present case. In the (n + 1)-component mixture which one has to deal with in order to

evaluate the effective potential, the special component x

interacts with all other replicas

via the potential

−N γ



α=1

q(x

, x

) =−γ



α=1



i, j=1

(

− x

)

. (10.3.11)

The effective potential is obtained using HNC closure for the (n + 1)-component mixture

in terms of the pair correlation function g

between the different replicas a and b.The

details of this calculation involving applying the HNC to the mixture can be found in the

original references (Morita, 1960; Morita and Hiroike, 1961; Mézard and Parisi, 1996).

10.3.2 A model calculation

We discuss here the results obtained by applying the above method to the case of a hard-

sphere potential (Cardenas et al., 1999) of diameter σ . With the choice r

=0.3 and o(r)

as a step function we obtain

o(r) =

1, for r ≤ 0.3,

0, for r > 0.3,

(10.3.12)

where length has been scaled with respect to σ . At a ﬁxed density of the hard-sphere sys-

tem, for a given value of q (where 0 < q < 1), the corresponding value of γ is obtained from

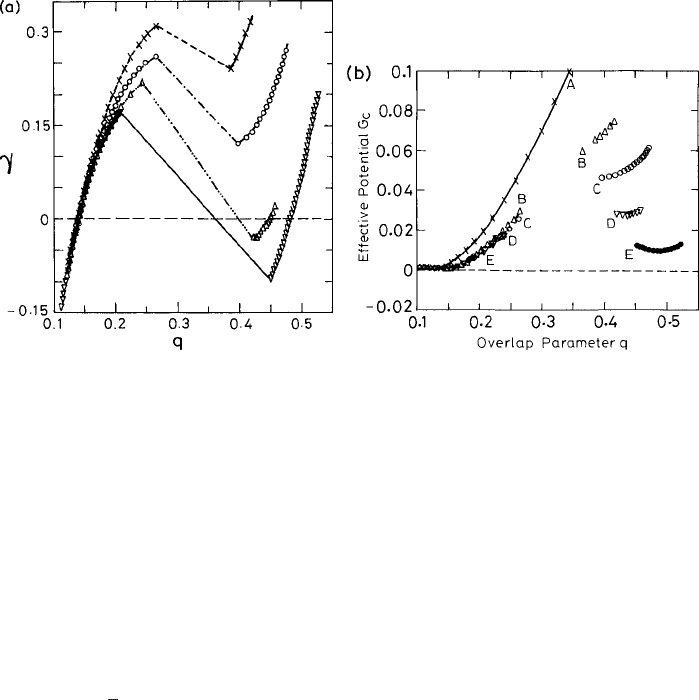
502 The thermodynamic transition scenario

Fig. 10.2 (a) The plot of q vs. γ (see the text) like a pressure–volume diagram for a hard-sphere

system using the hypernetted-chain-closure (HNC) structure. The different curves (from right to left)

are for densities n

=1.14, 1.17, 1.19, and 1.20. The lines connect the two branches correspond-

ing to the same density. (b) The effective potential (see the text) calculated for the results shown

in (a) for the hard-sphere system treated with HNC. The different curves from top to bottom corre-

spond to the densities in the earlier ﬁgure in increasing order. For low densities a single minimum is

present, whereas at high densities two minima exist, depicting the localized and delocalized states.

Reproduced from Cardenas et al. (1999). Both parts

 American Institute of Physics.

the optimization of (F(γ ) + qγ) for the pair of values of {q,γ}. The effective potential

(q) is then obtained by evaluating the RHS of (10.3.8) corresponding to this optimum

value of γ . The plot of γ with q is shown in Fig. 10.2(a) for a few ﬁxed densities. The

density n

is expressed in units of σ

here so that the close-packed f.c.c. structure has a

density n

√

Two qualitatively different types of minima are identiﬁed from this plot of q vs. γ .One

is at a small q value, which signiﬁes the delocalized liquid-like conﬁgurations with con-

tinuous motion of the ﬂuid particles. At high densities a new minimum, corresponding to

q ∼1, is observed. This corresponds to the glassy state in which the large-scale motions

are frozen, behaving as self-generated disorder. Only vibrational modes in the frozen states

occur, resulting in large overlap between the two replicas. Consider the speciﬁc results for

the hard-sphere system (Cardenas et al., 1999)showninFig. 10.2(a). For n

∼1.14, cor-

responding to γ>0, there are two values of the overlap parameter q at which the minima

are observed. Thus, at this density, in order to maintain the high-q state, the presence of the

coupling γ between the replicas is required. At relatively low densities in the limit γ →0,

only the delocalized state corresponding to small q is present. This is clear from the curves

corresponding to n

=1.14 and 1.17 in Fig. 10.2(a). However, as the density is increased

to n

∼1.19, even in the γ →0 limit, the high-q state appears. The latter represents the

frozen state with a high value for the overlap function q(x, y).

10.3 Self-generated disorder 503

The corresponding plots of the effective potential are displayed in Fig. 10.2(b). For den-

sities n

=1.01, 1.14, and 1.17, only a single minimum in the effective potential G

occurs.

These correspond to low q values conforming to the continuous liquid-like dynamics with

ergodic behavior. For the two densities n

=1.19 and 1.20, on the other hand, a high-q

minimum distinct from the one at low q appears. It is important to note that the relative

height of the two minima at a given density of the effective potential in Fig. 10.2(b) is not

an indicator of the relative stability of the two states. In fact, from our discussion above

it is clear that both of them are manifestations of the same phase. At high densities the

appearance of the secondary minimum at small q values signals the breaking of ergodicity.

The phase space breaks into many regions, which are mutually inaccessible. The overlap

between the conﬁgurations belonging to the different regions is small. The small-q min-

imum signiﬁes this. On the other hand, the overlap between conﬁgurations belonging to

the same region is high (q ≈ 1) and is manifested in the high-q minimum of the effective

potential.

The above calculation of the effective free-energy curve has been used to deﬁne the

conﬁgurational entropy of the supercooled state. Let 

denote the number of mutually

inaccessible regions into which the phase space splits. By virtue of the deﬁnition of the

conﬁgurational entropy S

we can relate it to 

=−k

ln 

. (10.3.13)

If we choose the conﬁguration y randomly, the probability that x will be in the same region

decreases as 1/

. From the perspective of the effective potential shown in Fig. 10.2(b),

the occurrence of such an event will imply going from the small-q state to the large-q state.

This implies activating over the barrier in the effective potential, i.e., G

, the difference

between the heights of the two minima. We therefore make the following link between the

effective potential and the conﬁgurational entropy:

exp



−





= exp

[

−NβG

]

, (10.3.14)

or TS

/N =G

. This result for S

is shown for various densities in Fig. 10.3 for a hard-

sphere system and leads to the identiﬁcation of the “Kauzmann density” ρ

=1.203 (cor-

responding to a packing-fraction value ϕ

=0.628) at which the conﬁgurational entropy

becomes zero. This is the extrapolated point at which a thermodynamic transition to an

ideal glassy phase is envisaged in the hard-sphere system.

The above-described approach to the study of structural glasses is in close analogy with

the methodology used for spin glasses. The idea of an effective potential for the liquids

was originally developed to study metastable states in mean-ﬁeld spin-glass models (Franz

and Parisi, 1997, 1998). The p-spin interaction models are the typical mean-ﬁeld systems

displaying a Kauzmann-like entropy crisis. The conﬁgurational entropy is an increasing

function of the temperature in the domain T

< T ≤T

and vanishes at T

. The overlap

504 The thermodynamic transition scenario

Fig. 10.3 The conﬁgurational entropy S

as deﬁned in eqn. (10.3.14) vs. density ρ

∗

for the hard-

sphere system using the effective potential. S

extrapolates to zero, giving the Kauzmann density

=1.203. Reproduced from Cardenas et al. (1999).

 American Physical Society.

function q(x, y) discussed above was also used (Franz and Parisi, 2000) for deﬁning

four-point functions χ

(t) similar to those which have been introduced in Section 4.4.2

for the structural liquids. The deﬁnitions (10.3.1)–(10.3.2) for q(x, y) can be interpreted

as a weighted product of densities ρ

(x) and ρ

(y) corresponding to the conﬁgurations X

and Y with weight function o(|x

− y

|). The four-point susceptibility is then a correlation

of the q(X, Y ) at two different times 0 and t .

(t) = β

+

, X

)

−



q(X

, X

)q(X

, X

)



(10.3.15)

To compute this correlation of the q-functions, we consider a system in equilibrium at t = 0

with Hamiltonian H (X) which evolves for positive times with a modiﬁed Hamiltonian

tot

(X) = H(X) − εq(X, X

). (10.3.16)

Linear response theory then obtains the correlation function as

(t) = β

+

, X

)

−



q(X

, X

)q(X

, X

)



∂

∂ε



q(X

, X

)



(10.3.17)

For the p-spin models the susceptibility diverges at the mean-ﬁeld transition at T

The model liquids discussed here are generally characterized by short-range repulsive

interactions. Since in the supercooled liquid slow dynamics takes place over enormous

length and time scales, the implications of having long-range interaction producing the

slow dynamics are important (they are discussed in the next section). Nucleation in disor-

dered systems with large-but-ﬁnite-range KAC-type (Kac et al., 1963; van Kampen, 1964;

Lebowitz and Penrose, 1966) interactions has been studied (Franz and Toninelli, 2004,

2005; Franz, 2005).

10.4 Spontaneous breaking of ergodicity 505

10.4 Spontaneous breaking of ergodicity

We now discuss the statistical mechanics of the supercooled liquid in keeping with the

scenario of an ideal glass transition that is characterized by the vanishing of the conﬁgu-

rational entropy S

at a point T =T

(say). This formulation, as we will see, also gives

rise in a natural way to a ﬁrst-principles approach to formulating the thermodynamics of

the amorphous solid state or the glass. In a standard thermodynamic description, above the

freezing point T

, the disordered liquid state with a (time-averaged) constant density has

the minimum free energy. The liquid cooled below its freezing point continues to remain

in the disordered state, provided that crystallization is avoided. The free energy of the

metastable liquid is obtained from a functional of a suitable order parameter ψ (say) for

the state. Generally ψ is the inhomogeneous density ρ(x), which is written in a parametric

form involving a set of coefﬁcients. The latter deﬁnes the multidimensional-space free-

energy landscape (FEL) (see also Section 4.3.2 for discussion). The supercooled liquid

is in a metastable state characterized by local minima of the free energy F[ρ], while the

crystalline state is the most stable state for the deepest minimum in this landscape. Distinct

basins exist in the FEL corresponding to different local minima of the free energy. This

picture described here is somewhat analogous to the potential-energy landscape (PEL) of

the N-particle system discussed earlier. However, the PEL is independent of temperature

whereas the FEL changes with temperature. At T = 0 all the local minima coincide with

the minimum of the potential energy as a function of the particle coordinates. In the vicin-

ity of the freezing point the hight-temperature behavior of the liquid is described in terms

of the single free-energy minimum for the uniform liquid state. In the deeply supercooled

state, well below the freezing point, the corresponding FEL breaks up into an exponen-

tially large number of basins with local minima. The metastable liquid is viewed as being

caught in one of these many possible basins. This transformation in the supercooled liquid

has been termed a spontaneous breakdown of ergodicity. In the case of structural glasses

which is the subject of interest here, this occurs without the presence of any quenched

disorder in the system.

Let us consider evaluation of the partition function for such a system. The partition func-

tion is obtained by equating the summation of the Boltzmann factor over different possible

states and has two main contributions. The ﬁrst one comes from the evaluation of the

Boltzmann weight with the system being conﬁned to a given basin having a characteristic

free-energy minimum. The number of such minima at a given temperature accounts for the

conﬁgurational entropy of the supercooled liquid. The second contribution involves differ-

ent states corresponding to a given basin, referred to as vibrations within the basin. This

accounts for the vibrational contribution to the entropy of the supercooled liquid. Indeed,

an idealized situation like this will require inﬁnite barriers between different states such

that the system conﬁned within a given basin is undergoing only vibrations around the

corresponding minimum. In mean-ﬁeld p-spin models in which every spin interacts with

every other spin (see Section 8.4 for more discussion) this is a more appropriate situation.

We will apply this scheme for evaluating the partition function in the structural glasses in

order to compute the thermodynamic properties of the glassy state.

506 The thermodynamic transition scenario

We begin with the ﬁrst part, namely the conﬁgurational contribution. We adopt the nota-

tion in which a particular basin α has a free energy F

and hence a free-energy density

= F

/N. With the above hypothesis of the FEL for the N -particle system being divided

into separate basins, the partition function Z

for the N -particle system is obtained by

summing up the contributions







x∈α

dx e

−β H(x)



−β Nf

(T )

, (10.4.1)

where H denotes the microscopic Hamiltonian as a function of phase-space variables

denoted as x and β =1/(k

T ) is the inverse temperature. At high temperature there is

only one global minimum of the free energy F(β) contributing to Z

. Close to T

there

may appear an exponentially large number of metastable states with energies higher than

F(β). However, the role of these metastable states is not “seen” in the evaluation of the

Gibbs partition function as long as their number does not compensate for their small (com-

pared with that of the global minimum) Boltzmann weight. At some temperature ∼

(say)

the number of metastable states becomes large enough to make up for the difference and

contribute to the partition function. In a system with ﬁnite-range interactions the ergodic-

ity breaking at

is not complete. The dynamics is slow during this stage, but activated

hopping processes can make the liquid reduce its free energy and ﬁnally relax to the liquid

state.

To describe the physics of the supercooled liquid below

, we need to analyze the

partition function evaluated as in eqn. (10.4.1). In the thermodynamic limit we will treat the

free energy f

as a continuous variable spanning over the range f

max

(T )> f

> f

min

(T )

at a given temperature T . The number of states corresponding to a given f is exponentially

large and is given by

( f ) ≡ exp



( f, T )





δ( f − f

), (10.4.2)

where S

( f, T ) denotes the conﬁgurational entropy by deﬁnition.

The partition function

is now obtained from the RHS of eqn. (10.4.1),



df ν

( f )e

−β Nf



max

min

df e

β N{TS

( f,T )− f }

. (10.4.3)

This scenario has often led to the conjecture that

is similar to the ideal transition temperature T

of the MCT described in

the previous sections. Such an interpretation presumably is more appropriate for the mean-ﬁeld

p-spin model. For a structural

glass, as we have seen, the dynamics is formulated for ﬂuctuations around the uniform liquid state, and ergodic behavior is

indeed recovered below

, even in the absence of any activated hopping processes.

It should be noted that this is only one particular way of deﬁning the conﬁgurational entropy using the above description of

the supercooled liquid in terms of the free-energy basins.

can also be deﬁned, as we have seen in previous sections, in

terms of local minima in the PEL or by dividing phase space at sufﬁciently low energy into many disconnected regions



described in the previous section.

10.4 Spontaneous breaking of ergodicity 507

In the thermodynamic limit (N →∞) the term which dominates the integral above cor-

responds to the free-energy density f = f

∗

for which the exponent {S

( f, T ) − β f } is a

minimum. Hence the optimum value f

∗

is obtained from the solution of

( f )

f =f

∗

. (10.4.4)

For high enough temperatures (which includes temperatures below T < T

but close to

) the saddle-point energy f

∗

lies between f

min

and f

max

. In keeping with the scenario of

a thermodynamic transition, the saddle point f

∗

shifts towards the corresponding f

min

(T )

as the liquid is further supercooled towards the Kauzmann temperature T

and ﬁnally

reaches f

∗

= f

min

at T

. The temperature T

marks the point below which the saddle point

sticks at f

∗

= f

min

(T ). In this scenario there is a phase transition in the liquid at T =T

It is a second-order transition since the free energy is continuous through the transition and

no latent heat is absorbed. The conﬁgurational entropy vanishes at T

and remains absent

for all T < T

. Only a small (nonexponential) number of valleys will contribute to the

partition function for T ≤ T

. These are the basins with free-energy minima at f

min

10.4.1 The replica method for self-generated disorder

An important contribution to our understanding of the FEL of the glassy systems and spon-

taneously broken ergodicity in systems without any quenched disorder came from the work

of Monasson (1995) in which an ingenious way of extending the replica trick to such sys-

tems was proposed. In this approach the conﬁgurational entropy S

of the liquid is obtained

by dealing with a composite system consisting of m replicas of the original system, with

their being coupled through a weak interaction. As we will see, this is quite different from

the replica approach which was applied to the spin-glass problem earlier (Mézard et al.,

1987). To illustrate this, let us consider a free-energy functional F

in terms of a coarse-

grained ﬁeld φ(x). For example, F[n] denotes the free-energy functional which depends

on the coarse-grained density function n(x) of the N -particle system treated as a ﬁeld.

For certain density distributions represented by the coarse-grained function n(x), the func-

tional F reaches a local minimum representing a metastable state. The equilibrium Gibbs

free energy for the system in terms of the ﬁeld φ(x) is obtained as

(β) =−β

−1



Dφ(x) exp{−β H [φ]}. (10.4.5)

The function space of φ(x) covers the minima corresponding to the different basins of

the FEL. Now, in order to compute the free-energy values at the bottom of a basin, we

consider the presence of a pinning ﬁeld ψ(x), which acts as an external quenched ﬁeld and

is coupled to φ(x ) with a coupling g > 0. The corresponding free energy is obtained as a

generalization of eqn. (10.4.5) to

[g,β]=−β

−1



Dφ(x) exp

−β H[φ]−



dx[ψ(x) − φ(x)]

. (10.4.6)

508 The thermodynamic transition scenario

Note that the free energy F

[g,β]is minimum when we have the pinning ﬁeld ψ(x) iden-

tical to the φ(x) corresponding to the minimum of the unperturbed free energy given by

eqn. (10.4.5). For a state in which ergodicity is spontaneously broken, spanning the func-

tion space of ψ(x) should therefore be able to pick up the contribution from the minima of

different basins in the FEL at temperature β

−1

. Let us therefore use F

[g,β]as a “Hamil-

tonian” for the ﬁeld ψ(x). The corresponding free energy F (in the limit in which the

coupling g goes to zero) at some chosen temperature

β =mβ is obtained as

β]=−

−1

lim

g→0





Dψ(x) exp

−

βF

[g,β]



=−

−1

ln Z

(

β). (10.4.7)

The corresponding internal energy will be computed using the relation since U =−(∂/∂

)

ln Z

β) =−

∂

ln Z

(

β)

∂

∂m

{

mF [β, m]

}

. (10.4.8)

In writing the last equality we have chosen β as a constant. In general, it is difﬁcult to

compute the integral on the RHS of eqn. (10.4.7). However, if m is chosen to be a positive

integer it is straightforward to compute the integral by introducing m identical replicas of

the original system (Monasson, 1995). The ﬁeld φ(x) for the composite system with dif-

ferent replicas is denoted as {φ}={φ

}{φ

}···{φ

}. It is straightforward to integrate

out the Gaussian ﬁeld ψ on the RHS of (10.4.7) to obtain the result

F[β,m]=−

βm

lim

g→0

⎡

⎣



μ=1

Dφ

(x)

× exp

⎧

⎨

⎩

−β



μ=1

H[φ

]−



μ<ν



[φ

(x) − φ

(x)]

⎫

⎬

⎭

⎤

⎦

≡−

βm

ln W, (10.4.9)

where W is the partition function and H (together with the inter-replica coupling of strength

g) is the Hamiltonian for the replicated system. In the next section we consider the calcu-

lation of the free energy of this replicated system, i.e., −β

−1

ln W. The quantities F(β, m)

and U(β, m) represent, at temperature β

−1

, the (per-replica) free energies and the internal

energies of the composite system, respectively.

If we now consider the limit m =1, the difference, i.e., β(U − F ), is equal to the

“entropy” of the original system. The quotes around the word entropy are intended to

indicate the peculiarity of the quantity obtained here with the special counting described

above. This is achieved using the pinning ﬁeld ψ(x), making it feasible to enumerate the

10.4 Spontaneous breaking of ergodicity 509

number of potential-energy basins in the FEL. This is the conﬁgurational entropy S

of the

supercooled liquid with spontaneously broken ergodicity. Note that it is different from

the standard entropy β

(∂F

/∂β) associated with the ﬁeld φ.Fromeqn. (10.4.8) we obtain

the useful result

= β



∂

∂m

F[β, m]



m=1

. (10.4.10)

Below T

eqn. (10.4.10) cannot hold, since it predicts a negative conﬁgurational entropy

for states having a lower free energy than F

. It follows from the deﬁnition (10.4.7) of

(

β). Physically, even at T < T

, freezing into a small (nonextensive) number of states

will still occur, and S

remains zero in these states. However, the effective temperature

β =βm associated with the pinning ﬁeld ψ remains pinned at β

for the physical system

and different from the actual temperature β for φ. Understanding the physics for T < T

will require analytically continuing the theory to the region m < 1. We will discuss this

case for the properties of the amorphous solid in the next section.

10.4.2 Free energy of the Replicated liquid

The free-energy landscape (FEL) of a high-temperature liquid has a single minimum cor-

responding to a uniform liquid state. In the supercooled state the FEL transforms to one

with an exponentially large number of metastable minima. This transformation is charac-

terized by the liquid developing a ﬁnite conﬁgurational entropy S

per particle. With the

model described above S

is obtained from eqns. (10.4.9) and (10.4.10). We express the

free energy and hence the conﬁgurational entropy S

in terms of the correlation matrix

G in the replica space. In this respect it is useful to exploit the symmetry in the space

of identical replicas to simplify the different elements of the matrix G of the correlation

functions,

=φ

(x)φ

(y)=G(x − y) for a = b (10.4.11)

= F(x − y) for a = b. (10.4.12)

We have assumed above that in the liquid state φ(x)=0. Hence in this case the off-

diagonal elements of the correlation matrix in the replica space are zero. With the spon-

taneous breakdown of the ergodicity there appear the distinct basins in the FEL, each of

which with has a nonzero value of φ(x) for the liquid. In this case, for the replicated

liquid, the off-diagonal elements of the correlation matrix φ

(x)φ

(y) (for a = b) are also

nonzero. If P

is the weight factor for the α-th state or the basin in the FEL, then



φ(x)φ(y)

, for a = b (10.4.13)



φ(x)

φ(y)

, for a = b. (10.4.14)

510 The thermodynamic transition scenario

The small extensive interactions between the identical copies or replicas force all the m

replicas to fall in the same state, i.e., simultaneously belong to the same free-energy basin.

The breaking of ergodicity, however, implies a coupling between replicas and nonzero off-

diagonal elements F(x −y) even in the g→0 limit.

Assuming the symmetry of the replica

indices, which is also present in the coupling (g) term on the RHS of (10.4.6), we obtain

the matrix G of correlation functions in the convenient form

G = (G − F )I + FE (10.4.15)

where I is the identity matrix and E has all its elements as unity, both matrices being of

size m ×m.

With purely Gaussian or quadratic Hamiltonian H,them dependence of replicated quan-

tity F[m] trivially drops out in the vanishing limit of the inter-replica coupling g. In that

case we have S

= 0. Hence consideration of non-Gaussian free energies is essential in

investigating the ergodicity-breaking transition. With the special form (10.4.15) of the cor-

relation matrix G, it follows that its inverse should also have a similar form (see below for

a proof of this). The inverse of the correlation matrix G corresponding to a non-Gaussian

theory is written in the form of the Schwinger–Dyson equation

−1

= G

−1

+  −

E (10.4.16)

which deﬁnes the self-energy matrix . G

is the correlation function in the absence

both of the nonlinearities and of the g-coupling. Since the different replicas are com-

pletely decoupled in this case, we have for the zeroth-order matrix G

= G

I. There-

fore, from eqn. (10.4.16) we argue that the self-energy matrix  should also have the

form (10.4.15)

 ={

− 

}I + 

E. (10.4.17)

Hence the inverse of the matrix G is obtained in the form

−1

={G

−1

+ 

− 

}I + 

E. (10.4.18)

Note that the Gaussian part of the correlation matrix is assumed to keep the form G

−1

I. We absorb the g-dependent part by redeﬁning 

and 

. We now use the fact that

any two matrices of the form (10.4.15) will have a product that is also of the same form.

Hence, with A

= a

I + b

E for i = 1, 2, we obtain that the product has the form

= a

I + (a

+ b

+ mb

)E. (10.4.19)

In case the of spin glasses De Dominicis (1978a) has noted that the correlation in the replica space can be obtained in terms of

the long-time limit of dynamic correlations or the Edward–Anderson order parameters. Hence, using the MSR method for the

dynamics, averages over the quenched randomness can be performed without relying on the corresponding replica trick in

which the replica index is taken to zero at the end.

We adopt here an opposite sign compared with that in eqn. (7.1.27) in Chapter 7 for the MSR theory.