Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

10.5 The amorphous solid 521

molecule and another is effectively rescaled here by a factor m. For small enough m,the

interaction between the particles is weak and the composite system is a liquid, which is

rather peculiar in nature. The thermodynamic properties of the amorphous glassy state

below T

are determined (Mézard and Parisi, 1999) in terms of those of this m-replicated

liquid (m < 1).

The free energy of the replicated system of m clones for T < T

is obtained from the

saddle-point contribution in eqn. (10.5.67). We denote the free energy as mF(m, T ).

Let

f = f

∗

denote the saddle point in the integral on the RHS of eqn. (10.4.7) and be obtained

from the solution of eqn. (10.5.68). Explicitly evaluating the saddle-point integral (10.5.67)

at f = f

∗

gives

mF (m, T ) =−

ln Z

= mf

∗

− TS

( f

∗

, T ). (10.5.69)

Each of the m systems does not reach the lowest possible free energy, but the composite

one does by balancing the free energy and the conﬁgurational entropy S

as given in eqn.

(10.5.69). The free energy f per replica and the conﬁgurational entropy S

are evaluated

from eqn. (10.5.69) and using the condition (10.5.68),

∗

∂

∂m

[

mF (m, T )

]

(10.5.70)

∂

∂m

[

F(m, T )

]

. (10.5.71)

The free energy of the cloned system F(m, T ) is a convex function of m having a maxi-

mum at m = m

∗

. This observation turns out to be consistent from the ﬁnal result which

follows. By virtue of eqn. (10.5.71), S

= 0atm = m

∗

.Form > m

∗

we run into an

unphysical situation since the RHS of eqn. (10.5.71) becomes negative.

How do we estimate the free energy in the glassy state at T < T

? Studying the cloned

liquid is useful in this respect since it helps us to locate the relevant minima in which

the system is frozen in terms of m

∗

(T ). However, the free energy at T < T

cannot be

obtained from the m→1 case of the cloned liquid described above. This is because the

phase transition to the nonergodic state occurs at m = m

∗

(T )<1. However, we can

determine the free energy below T

in terms of that of the cloned liquid state using the

fact that in the glassy state the conﬁgurational entropy S

is zero. It then follows from

eqn. (10.5.71) that the free energy per replica F(m, T ) is independent of m. Hence the

free energy F(m = 1, T ) of the original system is obtained by mapping from F(m =

∗

(T ), T ). The latter is evaluated from the liquid-state free energy at the boundary m =

∗

(T ) using the fact that the free energy is continuous through the transition at m

∗

.This

is the crucial mapping of the free energy of the glass at T < T

into that of the replicated

“liquid” consisting of molecules with m atoms.

We keep the notation of eqn. (10.4.7) introduced in the previous section for the liquid state above the thermodynamic

transition of vanishing entropy.

522 The thermodynamic transition scenario

To summarize the method, we are required to estimate the replicated free energy

mF (m, T ) for the molecular liquid phase with each molecule consisting of m atoms. At

T < T

, an analytic continuation in the unphysical range of m < 1forF (m, T ) actu-

ally maps the replicated-liquid free energy into that of the glassy solid. In the present

scenario, the supercooled liquid when cooled slowly enough undergoes a second-order

phase transition at T = T

and the conﬁgurational entropy remains zero in the glassy

phase following a kink at the transition point. The glassy state is caught in one of the

subexponential number of free-energy minima for the system. In some sense this map-

ping is reminiscent of the mapping of the crystalline solid into a low-density liquid in the

weighted-density-functional theories of the freezing transition discussed in Chapter 2.

10.5.1 The Mézard–Parisi model

The idea sketched out above for obtaining the thermodynamic properties of the glass is sim-

ple and based on plausible hypotheses. The glassy state is mapped here into a replicated-

liquid state with N molecules, each having m atoms. However, given the fact that one has to

focus here on the unphysical domain m < 1, implementing the scheme appears somewhat

strange. We are required to analytically continue the expressions for the free energy into

the domain m < 1. In order to develop a statistical-mechanical formulation starting from a

two-body interaction potential v(r), we therefore need to start from a microscopic Hamil-

tonian. In the following we consider an explicit formulation (Mézard and Parisi, 1999a)of

the scheme proposed above for summing the partition function in terms of contributions

from different free-energy basins. The partition function for the N -particle system moving

in a volume V in d dimensions is obtained as

N !

i=1



exp

⎡

⎣

−

N 



i, j=1

v(r

−r

)

⎤

⎦

. (10.5.72)

The thermodynamic limit in the present context involves taking N, V →∞, with the den-

sity n = N/ V remaining ﬁxed. We construct the replicated liquid by introducing the m

identical replicas of the original system. We have m clones of each particle in the compos-

ite system forming a molecular liquid. We denote the position of the ith particle of replica

a as r

with a ∈1, 2,...,m. To avoid clutter, we will write the position x dropping the

vector notation here. The partition function Z

of this composite system is obtained as

i=1

a=1



N !

exp



−β H

"

. (10.5.73)

is the Hamiltonian for the composite system consisting of the m clones of the original

liquid,

⎧

⎨

⎩

N 



i, j=1

(

−r

)

− 



i, j=1

m 



a,b=1

(

−r

)

⎫

⎬

⎭

. (10.5.74)

10.5 The amorphous solid 523

In the above, as well as in the following, we adopt the notation that the prime in the sum

indicates the absence of the a =b term. w(r) is the weak attractive potential of a short

range, which is less than the typical inter-particle distance in the solid state. We now test

whether a temperature T

can be identiﬁed from the above model such that for T < T

the free energy F (m, T ) of the replicated liquid reaches a maximum corresponding to

∗

(T )<1. For this F(m, T ) has to be evaluated for real positive values of the param-

eter m. In the ﬁnal calculation, we will take lim

w→0

after taking lim

N →∞

.Webeginby

evaluating the partition function given in eqn. (10.5.74) with a simple-harmonic approx-

imation for the Hamiltonian in terms of u. Several other methods have been developed

(Mézard and Parisi, 1999b) for the problem, but we focus our discussion on the harmonic

approximation.

The location r

of the i th atom of replica “a”inthem-atom molecular liquid is expressed

in terms of the center-of-mass coordinate r

= r

+ u

, (10.5.75)

where r

is the center-of-mass coordinate for the ith molecule consisting of m identical

atoms. By deﬁnition, r

is obtained as



. (10.5.76)

Hence, from eqn. (10.5.75), it follows that sum of individual displacements u

for the ith

molecule of the cloned system must satisfy



= 0. (10.5.77)

In the expression (10.5.73) for the partition function Z

, we make a change of variables





→



, u



for a =1, 2,...,m, and i =1, 2,...,N. It is useful to check some details

of this coordinate transformation in order to keep track of the proper m dependence in

the partition function Z

. There are in total mNd displacement variables u

and Nd

center-of-mass coordinates r

. Taking into account the Nd delta functions due to the con-

straints given by (10.5.77), the total number of independent variables is (mN − N + N )

d =mNd as expected. With this change of variables, taking into account the factor of m

due to the Jacobian, the partition function is obtained as

N !





i=1







× exp

⎧

⎨

⎩

−

N 



i, j=1



(

−r

)

−





m 



a,b=1

(

− u

)

⎫

⎬

⎭

. (10.5.78)

524 The thermodynamic transition scenario

In writing the above equation, we have simpliﬁed the notation by using on the RHS the

following abbreviations for the differential elements:

≡

i=1



, du

≡

i=1

a=1



. (10.5.79)

The inter-particle potential v

(

−r

)

is expanded in terms of the displacements u

around the respective centers of mass as

(

−r

)

= v

(

−r

+ u

− u

)

= v(r

−r

) +

∞



p=2

(

− u

)

( p)

−r

), (10.5.80)

where v

( p)

(r) denotes the pth-order derivative of the two-body potential v(r).Usingthe

above expression for v in the partition function, we obtain

N !







× exp

⎧

⎨

⎩

−

N 



i, j=1

⎡

⎣

v(r

−r

) +

∞



p=2



− u



( p)

−r

)

⎤

⎦

−





a,b=1



− u



⎫

⎬

⎭

N !



exp

⎧

⎨

⎩

−

βm

N 



i, j=1

v(r

−r

)

⎫

⎬

⎭

, (10.5.81)

where we have denoted the product of Nd delta-function constraints with δ





(

)

≡

i=1







. (10.5.82)

The integral I

representing the contributions from the vibrations of the individual atoms

about the corresponding center of mass is deﬁned as



(

)

exp[−A

]. (10.5.83)

The quantity A

in the exponent on the RHS of eqn. (10.5.83) represents the inter-replica

interaction. For low temperatures we will make the crucial approximation that the u

are

small so that the expansion in the second term in the exponent on the RHS of (10.5.80)

is considered only up to quadratic order (p =2). With this approximation the partition

function reduces to an integral of the quantity I

over the center-of-mass coordinates.

10.5 The amorphous solid 525

We express the full partition function Z

as an average over the center-of-mass coordi-

nates, which we denote by putting a subscript ∗ on the angular brackets:

⎡

⎣

N !



exp

⎧

⎨

⎩

−

βm

N 



i, j=1

v(r

−r

)

⎫

⎬

⎭

⎤

⎦

= Z

∗

)I



∗

, (10.5.84)

where Z

denotes the partition function for a system involving only the motion of the

center of mass of the m-atom molecules at a temperature T

∗

=T /m. The integral I

rep-

resents the contributions from the vibration of the atoms around the corresponding center

of mass and is obtained by performing the Gaussian mNd-dimensional integrals over the

variables with Nd delta functions. We describe this calculation in Appendix A10.3.

Here we just continue with the result,

= C

exp



−

m −1

Tr ln M



, (10.5.85)

where the matrix M, which is dependent on the center-of-mass coordinates {r

} and the

corresponding Hessian matrix for the interaction potential v(r

−r

), is obtained as

iμ, jν

= δ



(μν)

−r

) − v

(μν)

−r

), (10.5.86)

where we have used the abbreviation v

μν

≡ ∂

∂

v(r

− r

). The constant C

is obtained

in Appendix A10.3 as

= m

Nd/2

(2π)

(m−1)Nd/2

. (10.5.87)

On substituting this result and (10.5.85) into eqn. (10.5.84), we obtain the total partition

function Z

evaluated in the harmonic approximation,

= Z

∗

)



exp

−

m −1

Tr ln M

∗



. (10.5.88)

The above expression therefore approximates the partition function of the molecular

liquid with m replicas at temperature T as a sum of two contributions: ﬁrst, the contribution

from the center-of-mass motion of the r

,fori =1,...,N molecules, each with m

atoms at an effective temperature T

∗

=T /m; and second, the contribution in the square

brackets on the RHS of eqn. (10.5.88) from the vibration modes giving rise to the Tr ln M

term. Evaluating the second part described by M, which is related to the Hessian matrix

of the glassy state, requires further approximations. This contribution, which accounts for

the vibration of the individual atoms in the ith molecule around the center of mass at r

,is

evaluated in a non-self-consistent approximation, i.e., we ignore the feedback effects from

the vibration on the {r

} coordinates. In this approximation we write

exp



−

(m −1)Tr ln M

.

∗

≈ exp



−

(m −1)



Tr ln M



∗



. (10.5.89)

526 The thermodynamic transition scenario

This is termed the quenched approximation (Mézard and Parisi, 1999b). Even after this

approximation has been made, evaluation of the above term involving the “trace log” of the

matrix M is difﬁcult. An approximate evaluation of the RHS of eqn. (10.5.89) is given in

Appendix A10.3. The deﬁnition of the free energy F(m, T ) per molecule of the replicated

liquid is given in eqn. (10.5.69). The partition function Z

includes contributions separated

into center-of-mass and vibrational parts as given by eqn. (10.5.88):

βF(m, T ) =−

ln Z

=−



ln Z

∗

) + ln C

−

m −1



Tr ln M



∗



. (10.5.90)

The quantity f

intheﬁrsttermontheRHSofeqn. (10.5.92) denotes the free-energy

density (per particle) of this center-of-mass system at a temperature T

∗

= T /m,

∗

) =−

ln Z

. (10.5.91)

∗

) is obtained from standard integral-equation theories of liquid-state physics.

Using the results from eqns. (10.5.87) and (A10.4.16), we obtain the free energy F(m, T )

per replica as

βF(m, T ) = β f

∗

) +

m −1

−

(2π)

m−1

, (10.5.92)

where I

in the second term on the RHS is obtained as





(2π)



[˜a

(k)]+(d − 1)L

[˜a

⊥

(k)]



−



dr g

∗

(r)



μν

(μν)

(r)

¯r

⎤

⎦

+ d ln(βr

). (10.5.93)

Using the above analytic expression in eqn. (10.5.92) requires application of the so-called

quenched approximation, as well as treating multi-particle correlations with a superposi-

tion approximation. These are discussed in Appendices A10.3 and A10.4. It is important

to note here that evaluating this approximate expression for the free energy requires only

knowledge of the thermodynamic properties of the N -particle system in which the ith par-

ticle is located at the center of mass of the corresponding molecule in the replicated liquid.

The interaction potential between the particles at i and j is v(r

−r

The integral I

in the second term on the RHS is obtained in terms of the pair cor-

relation function g

∗

and derivatives of the interaction potential v(r). The function L

deﬁned as L

(x) = ln(1 − x) +x +x

/2. The quantities ˜a

(k) and ˜a

⊥

(k) appearing in the

arguments of L

are obtained from the Fourier transform of g

∗

(r)v

(μν)

(r) with respect to

the wave vector k. In the isotropic system the transformed function is expressed in terms

10.5 The amorphous solid 527

of two components, which are referred to as “parallel” and “perpendicular” with respect to

the wave vector,



dr g

∗

(r)



∂

v(r)

∂r



ik · r

(k) +



μν

−



⊥

(k). (10.5.94)

For the arguments of the function L

on the RHS of eqn. (10.5.92), we deﬁne ˜a

(k) =

(k)/¯r

and ˜a

⊥

(k) =a

⊥

(k)/¯r

.Them dependence of expression (10.5.92) is totally ana-

lytic and is therefore suitable for analytically continuing F (m, T ) to the region m < 1of

the parameter space.

The above model was studied for different interaction potentials. For soft-sphere poten-

tials v(r) =1/r

in three dimensions (Mézard and Parisi, 1999a). The Kauzmann temper-

ature T

is obtained from eqn. (10.5.68) using the calculated value of the conﬁgurational

entropy. By computing the free energy f

(T /m) and the pair correlation function g

∗

(r)

with the hypernetted-chain approximation, the analytic expression for the replicated free

energy is evaluated. By locating the maximum of the free energy, m

∗

(T ) is obtained. The

Kauzmann temperature corresponds to m

∗

) =1. In the present case this is obtained

at T

=0.194 and density n

=1.0. This temperature and density together correspond to

the dimensionless parameter 

eff

−1/4

 1.51. The corresponding result observed

in computer simulations of the same system is  =1.6(Bernuet al., 1985; Roux et al.,

1989). The various properties of the ideal glass phase follow from the model in a natu-

ral way. For the soft-sphere interaction potential the various parameters characterizing the

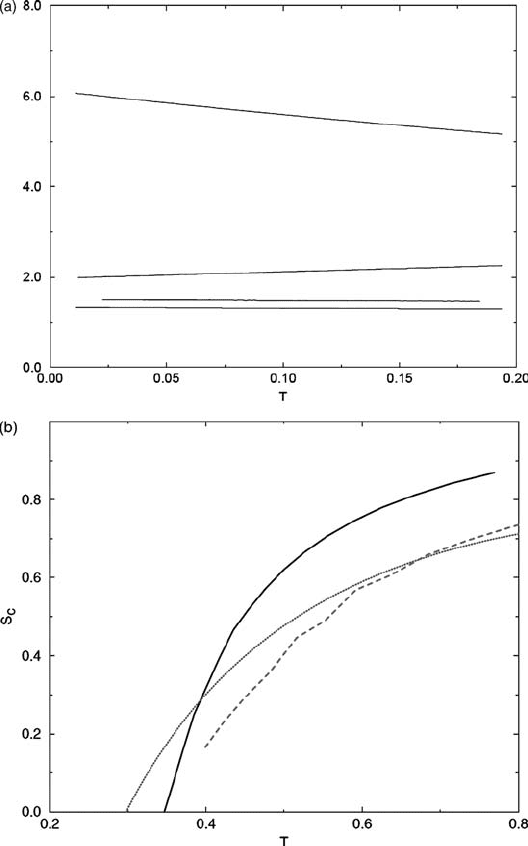
glassy state are shown in Fig. 10.5(a). The effective temperature is given by T

∗

=T /m

∗

where m

∗

is the value of m at which the free energy has a maximum. T

∗

varies very little

in the glass phase, remaining close to T

.BelowT

, in the glass phase the speciﬁc heat

computed from the derivative of the internal energy remains almost constant at

.Thisis

the result expected from the Dulong–Petit law for a classical solid, which is the model fol-

lowed in the present analysis. The model was applied to other systems (which have more

commonly been investigated in order to study the glass transition), namely binary mixture

of soft spheres (Coluzzi et al., 1999). More recently, this model has been applied to the

study of hard-sphere ﬂuids (Parisi and Zamponi, 2010). The (Kauzmann) packing fraction

at which the conﬁgurational entropy vanished is 0.62, which is comparable to the result

of 0.628 obtained from Fig. 10.5(b) with application of the result (10.3.14).

The nature of the proposed transition at T

is somewhat ambiguous. The conﬁgurational

entropy S

vanishes at T

and remains zero for T < T

. The thermodynamic transition at

characterized by the conﬁgurational entropy S

remains continuous on passing through

the transition with a kink at T

. No latent heat is absorbed. In this sense the thermodynamic

transition at T

is continuous. On the other hand, we deﬁne below an order parameter,

which changes discontinuously on passing through the transition. The square of the size of

the cage seen by each atom in the system is deﬁned as

A =

1

−x





. (10.5.95)

528 The thermodynamic transition scenario

Fig. 10.5 (a) The various quantities characteristic of the glass phase vs. temperature. From top to

bottom: the inverse effective temperature 1/T

∗

=βm of the reference liquid, the internal energy,

the speciﬁc heat, and the quantity 100A/T ,whereA is the square of the cage radius deﬁned in

eqn. (10.5.95). Reproduced from Mézard and Parisi (1999a). (b) The conﬁgurational entropy S

the binary Lennard-Jones system. The full curve shows the theoretical prediction obtained from the

Mézard–Parisi model using cloned liquid (Coluzzi et al., 1999). The dashed curve shows the results

from the simulations of Sciortino et al. (2000) using an inherent-structure approach to the potential-

energy-landscape studies. The dotted curve shows the results from simulations by Coluzzi et al.

(2000).

 Institute of Physics.

10.5 The amorphous solid 529

In the ergodic liquid state, when the particles are not localized, the inverse A

−1

vanishes.

This inverse cage size changes discontinuously at the transition, as is evident in the way the

model is constructed. In the glass phase the inverse of A is ﬁnite and the partition function

is evaluated by approximating the dynamics in terms of harmonic vibrations around the

center-of-mass coordinates. Naturally, A ∝ T for the glass phase. The speciﬁc heat also

jumps from its liquid-state value above the transition to one close to that of the crystalline

state below the transition.

The thermodynamic entropy is computed from the formula (10.5.71) obtained above

using the analytic form (10.5.92) for the free energy,

∂

∂m

[

F(m, T )

]

m=1

∗

∂ f

∗

)

∂m

m=1

−

[

d ln(2πe) − I

]

= S

liq

− S

sol

, (10.5.96)

where S

liq

is the entropy of the liquid,

∂ f

∗

)

∂m

∂T

∗

∂m

∂

∂T

∗

)

∗

liq

∗

), (10.5.97)

and T

∗

= T at m = 1. S

sol

represents the entropy of the harmonic solid, which is given by

sol

{

d ln(2πe) − I

}

. (10.5.98)

Indeed, as is clear from the above, we are computing the conﬁgurational entropy S

of the

supercooled liquid by subtracting from the liquid-state entropy the vibrational entropy in

the supercooled state. The latter is obtained by performing a harmonic expansion around

the center-of-mass coordinates. S

is zero at T =T

.InFig. 10.5(b) the theoretically calcu-

lated conﬁgurational entropy of the BMLJ system obtained from the formulation described

above is compared with that of models studied with computers using potential-energy

landscapes.

The above calculation of the conﬁgurational entropy S

for T > T

by going to the

m =1 limit of the center-of-mass contribution for the cloned molecular liquid is in fact

similar to the analysis of the previous section. In the present context, however, the partition

function is evaluated by performing the phase-space integrals in the harmonic approxima-

tion. The calculation presented here in terms of the short-range interaction potential is not

motivated to locate the spontaneous breaking of ergodicity from the normal liquid state.

Assuming the occurrence of such a transition, the thermodynamic properties of the amor-

phous solid (with S

=0) are obtained here using the microscopic interaction potential as

an input.

It is useful to note here that the replica index m

∗

(T ) depends linearly on the temperature

T . This is similar to the case of one-step replica symmetry breaking, which was originally

530 The thermodynamic transition scenario

introduced in the context of spin glasses (Mézard et al., 1987). Kirkpatrick and Thirumalai

(1987a) observed the analogy between the phase transition of discontinuous spin glasses

and the thermodynamic glass transition. We have discussed in Section 8.4 the close analogy

between the (dynamic) ergodic–nonergodic transition in p-spin models and that predicted

for structural glasses. Indeed, Kirkpatrick and Thirumalai in their 1987 work discussed

the possibility of a thermodynamic transition as a one-step replica symmetry breaking

at a temperature below the dynamic transition at T

. A similar replica approach has been

applied to the density-functional model for studying the phase diagrams of classical liquids

in a quenched random pinning potential by Thalmann et al. (2000) as well as for computing

correlations in a ﬂux liquid in a strongly anisotropic, layered superconductor with random

point pinning sites, as was proposed by Menon and Dasgupta (1994). The consequences of

long-range interaction for glassy behavior have also been studied (Rostiashvili and Vilgis,

2000a, 2000b) using the old type of replica approach, in which the replica index going to

the limit zero is to be invoked at the end.

It is important to note here the difference between the uses of replicas in the cases of a

spin glass and a structural glass. For spin glasses the replicas are used as a computational

trick to calculate the average of the logarithm of the partition function, and in the end

one needs to take the replica index to the limit zero. On the other hand, in the above

discussion of the thermodynamics of structural glasses the idea of replicas has a more

physical interpretation (Derrida, 1981; Gross and Mézard, 1984). In the structural glass

there is no quenched disorder and hence there is no need to average over the logarithm of

the partition function. Replicas are introduced here as a means to locate the spontaneous

ergodicity-breaking transition or to study properties of the amorphous solid state within the

framework of equilibrium statistical mechanics. We do not need to take the “zero-replica”

limit. However, there is an analytic continuation in the number of replicas m becoming less

than 1. An alternative way of describing the glassy state is to introduce a real coupling of

strength γ (see Section 10.3.1) with another system, which has thermalized. In the latter

case, however, the use of replicas to compute the logarithm of a partition function is in fact

similar to that for the spin-glass problem.