Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond
Подождите немного. Документ загружается.


9.3 A mean-field model 461
∂
∂t
+ z(t)
C(t, t
) =
t
0
ds
!
(t, s)R(t
, s) + (t, s)C(s, t
)
"
−
t
t
ds (t, s)R(t
, s). (9.3.25)
We consider first the second integral on the RHS. In the FDT limit with s lying between t
and t
, TTI holds and R(t
, s) ≡ R(t
− s) is related to the correlation function C(t
− s)
through the relation (9.3.23). Hence the second term on the RHS reduces to the form
−
t
t
ds
F
(t − s)
∂
∂s
C
F
(t
− s), (9.3.26)
where the subscript F denotes the FDT regime in which TTI holds. Next we consider the
first integral on the RHS of eqn. (9.3.25). The limits of this definite integral are split into
two parts,
I (t, t
) =
t
0
ds
!
(t, s)R(t
, s) + (t, s)C(s, t
)
"
≡
t−δ
0
+
t
t−δ
. (9.3.27)
The time scale δ is chosen such that for the FDT regime (of t and t
) in the second integral
on the RHS of (9.3.27) the relation (9.3.23) holds. Thus δ represents a time scale much
smaller than t or t
. On the other hand, for the first integral on the RHS of (9.3.27) the
correlation and response functions have time arguments that are sufficiently separated that
TTI does not hold. This is the aging regime. The RHS of (9.3.27) is thus obtained as
I (t, t
) =
t−δ
0
ds
!
A
(t, s)R
A
(t
, s) +
A
(t, s)C
A
(s, t
)
"
+
t
t−δ
ds
!
F
(t, s)R
F
(t
, s) +
F
(t, s)C
F
(s, t
)
"
≡ I
A
+ I
F
, (9.3.28)
where the subscripts A and F, respectively, denote the corresponding quantities for the FDT
and aging regimes. In the aging regime the correlation and response functions are written
in terms of scaling functions as
C
A
(t, t
) = qφ
h(t
)
h(t)
, R
A
(t, t
) =
h
(t
)
h(t)
R
h(t
)
h(t)
, (9.3.29)
.
where h(t) is a monotonically ascending function of time and the prime indicates a deriva-
tive with respect to its argument. q is the nonergodicity parameter and the scaling function
has the property φ(λ → 1) = 1. This is in keeping with the form of the correlation
and response functions seen in simulations and experiments on aging. In the simplest case,
when h(t) ∼ t (Bouchaud, 1992; Bouchaud and Dean, 1995), the above relations reduce to
C
A
(t, t
) = qφ(t
/t), R
A
(t, t
) = t
−1
R(t
/t). (9.3.30)

462 The nonequilibrium dynamics
Using the ansatz (9.3.29), the integral I
A
in (9.3.28) reduces to the form
I
A
=
t−δ
0
dt
∞
p=2
a
p
q
p−1
φ
p−1
(λ
)
dλ
dt
R(λ
)
+ ( p − 1)q
p−2
φ
p−2
(λ
)
dλ
dt
R(λ
)qφ(λ
/λ)
=
1−δ/t
0
dλ
∞
p=2
a
p
q
p−1
R(λ
)
φ
p−1
(λ
) + ( p − 1)φ
p−2
(λ
)φ(λ
/λ)
,
(9.3.31)
where we have changed the integration variable t
to λ
= h(t
)/ h(t) and defined λ =
h(t
)/ h(t). In the limit t, t
→∞and with δ much smaller than both t and t
, this leads to
λ → 1. The integral I
A
is now obtained as
I
A
=
∞
p=2
a
p
pq
p−1
I
q
, (9.3.32)
where the integral I
q
is defined as
I
q
=
1
0
dλ
φ
p−1
(λ
)R(λ
). (9.3.33)
The integral I
F
in (9.3.28) is calculated by applying the relation (9.3.23). Using the explicit
forms for and , we obtain
I
F
=
∞
p=2
a
p
t
t−δ
ds
C
p−1
F
(t − s)
∂
∂s
C
F
(t
− s) +C
F
(t
− s)
∂
∂s
C
p−1
F
(t − s)
=
∞
p=2
a
p
t
t−δ
ds
∂
∂s
C
p−1
F
(t − s)C
F
(t
− s)
=
∞
p=2
a
p
!
C
F
(t − t
) − q
p
"
. (9.3.34)
In writing the last equality we have used the constraint condition that C(t, t) = C
F
(0) = 1
and that the time scale δ by definition ensures that both C
F
(δ) and C
F
(δ − (t − t
)) → q.
Now, by combining the results of (9.3.32) and (9.3.34), we obtain for the integral I (t, t
)
the result
I (t, t
) =
∞
p=2
a
p
{C
F
(t − t
) − q
p
}+pq
p−1
I
q
. (9.3.35)

9.3 A mean-field model 463
Evaluating the RHS of eqn. (9.3.25), using the results of (9.3.26) and (9.3.35), and making
some rearrangement of variables, eqn. (9.3.14) finally reduces to the form
∂
∂τ
C
F
(τ ) =−z
∞
C
F
(τ ) −
τ
0
dτ
1
F
(τ − τ
1
)
∂
∂τ
1
C
F
(τ
1
)
+
∞
p=2
a
p
C
F
(τ ) − q
p
+ pq
p−1
I
q
, (9.3.36)
where z
∞
denotes the Lagrange multiplier z(t) in the limit t →∞. We can rearrange the
above equation further to obtain the following result for the TTI correlation function C(t )
(we drop the subscript F from now on for simplicity):
∂
∂t
+ 1
C(t) +
t
0
dτ(t − τ)
∂
∂τ
C(τ ) +˜z
∞
[C(t) − 1]
= 1 − z
∞
+
∞
p=2
a
p
1 − q
p
+ pq
p−1
I
q
, (9.3.37)
where ˜z
∞
is defined as
˜z
∞
= z
∞
− 1 −
∞
p=2
a
p
. (9.3.38)
The RHS of eqn. (9.3.37) is computed from the expression for z(t) given by eqn. (9.3.18).
From the definition (9.3.27) it follows that
z(t) = 1 + I (t, t
+
). (9.3.39)
On taking the t →∞limit of the above equation, we obtain, by applying the constraint
C(t, t) = 1 and using the result (9.3.35),
z
∞
= 1 +
∞
p=2
a
p
1 − q
p
+ pq
p−1
I
q
, (9.3.40)
implying that the RHS of eqn. (9.3.37) is zero. The TTI equation for the correlation
function in the FDT regime is therefore obtained as
∂
∂t
+ 1
C(t) +
t
0
dτ(t − τ)
∂C(τ )
∂τ
+˜z
∞
[C(t) − 1]=0. (9.3.41)
Equation (9.3.15) for the response function R also reduces to the same TTI equation
(9.3.41) in the FDT limit. To see this, it is best to work with the integrated response function
M(t, t
) defined as
M(t, t
) =
t
t
R(t, s)ds. (9.3.42)

464 The nonequilibrium dynamics
In the FDT regime, on applying (9.3.23), the above definition reduces to
M(t, t
) =
t
t
∂
∂s
C(t, s)ds = 1 −C(t, t
), (9.3.43)
since the spherical constraint ensures that C(t, t ) = 1. Now, by integrating eqn. (9.3.15)
for the response function R(t, s) from s = t
to t, we obtain the equation
∂
∂t
M(t, t
) =−z(t)M(t, t
) + 1 +
t
t
ds
t
s
dt
(t, t
)R(t
, s). (9.3.44)
Let us focus on the integral in the last term on the RHS of (9.3.44).Weshowin
Appendix A9.2 that this integral reduces to the form
τ
0
dτ
(τ − τ
)
∂
∂τ
C(τ ) +[1 − C(τ )]
∞
p=2
a
p
, (9.3.45)
where τ = t − t
. Thus eqn. (9.3.44) reduces in the FDT regime to the following form:
∂
∂τ
M(τ ) =−z(t)M(τ ) +1 +
τ
0
dτ
(τ −τ
)
∂
∂τ
C(τ ) +[1 − C(τ )]
∞
p=2
a
p
.
(9.3.46)
Using the relation (9.3.43) in the FDT limit as M(τ) = 1 − C(τ),forlarget the above
equation reduces to
∂
∂τ
+ 1
C(τ ) +˜z
∞
[C(τ ) − 1]+
τ
0
dτ
(τ − τ
)
∂
∂τ
C(τ
) = 0, (9.3.47)
where ˜z
∞
is as given by eqn. (9.3.38). Thus both the correlation-function and the response-
function equations, (9.3.14) and (9.3.15), respectively, reduce in the FDT limit to the
identical form given by either eqn. (9.3.47) or eqn. (9.3.41). This form is very similar
to the basic equation (8.1.8) of the mode-coupling theory for structural glasses (discussed
earlier in Section 8.1.1), apart from there being an inertial term in the latter. On the other
hand, the term proportional to ˜z
∞
is peculiar to the case of the spherical spin model. The
latter makes the dynamics somewhat different in this case below the dynamic-transition
point. From the long-time limit of eqn. (9.3.47) we obtain for the nonergodicity parameter
(NEP), i.e., the long-time limit of the correlation function q, the following equation:
− z
∞
+
∞
p=2
a
p
(1 − q
p−1
) =−
1
1 − q
, (9.3.48)
where z
∞
is given by the relation (9.3.40). The solution of these equations gives the value
of the NEP as well as the dynamic-transition point (in terms of the critical couplings a
p
).
However, for obtaining z
∞
we need the solution for the correlation and response functions
in the aging regime involved in the definition of I
q
(see eqn. (9.3.33)). This is discussed
next.
9.3 A mean-field model 465
9.3.3 The aging regime
For t and t
both going to infinity in such a way that (t − t
)/t
∼ O(1) analytic solutions
for the correlation and response functions in the aging regime, denoted by C
A
(t, t
) and
R
A
(t, t
), respectively, are obtained from (9.3.14) and (9.3.15) by separating the integrals
appearing in each equation into contributions coming from the aging and FDT regimes.
In the present case both t and t
are large, and also they are very widely separated. Two
times δ and δ
enter the problem, respectively separating (as in the previous section) the
corresponding time scales t and t
into FDT and aging regimes. Since t and t
are very
widely separated, the time derivatives on the LHS of both (9.3.14) and (9.3.15) can be
ignored. We analyze the two equations below.
The equation for the correlation function
From eqn. (9.3.14) for the correlation function C(t, t
) we obtain, on setting the LHS of
this equation to zero in the aging regime,
0 ≈−z
∞
C(t, t
) +
t
−δ
0
ds
A
(t, s)R
A
(t
, s) +
t
t
−δ
ds
A
(t, s)R
F
(t
, s)
+
t−δ
0
ds
A
(t, s)C(s, t
) +
t
t−δ
ds
F
(t, s)C
A
(s, t
). (9.3.49)
The subscripts A and F in the kernels and denote the corresponding quantities in the
aging and FDT regimes, respectively. The integrals on the RHS of eqn. (9.3.49) are denoted
as I
i
(i = 1,..., 4). Equation (9.3.49) therefore reduces to
0 =−z
∞
qφ(λ) +
4
i=1
I
i
. (9.3.50)
Note that in the third integral (I
3
)ontheRHSofeqn. (9.3.49) we do not indicate a subscript
on the correlation function C(s, t
).Ass varies from 0 to t − δ the correlation function
C(s, t
) passes through both the aging and the FDT regime. For 0 ≤ s ≤ t
− δ
and also
for t
+ δ
≤ s ≤ t − δ, the correlation function has the aging behavior C
A
; and for the
range t
−δ
≤ s ≤ t
+δ
it has FDT behavior C
F
. Therefore this integral I
3
separates into
three integrals as follows:
I
3
=
t
−δ
0
ds
A
(t, s)C
A
(s, t
) +
t
+δ
t
−δ
ds
A
(t, s)C
F
(s, t
)
+
t−δ
t
+δ
ds
A
(t, s)C
A
(s, t
)
≡ I
31
+ I
32
+ I
33
. (9.3.51)

466 The nonequilibrium dynamics
We compute the integrals I
i
(i = 1,...,4) on the RHS of eqn. (9.3.50) in Appendix A9.2.2
to obtain the following result:
0 = qφ(λ)
⎡
⎣
−z
∞
+
∞
p=2
a
p
(1 − q
p−1
) + (1 −q)
∞
p=2
a
p
q
p−2
φ
p−2
(λ)
⎤
⎦
+
∞
p=2
a
p
q
p−1
&
( p − 1)
1
0
dλ
R(λ
)φ
p−2
(λ
)φ({λ
/λ}
sg(λ−λ
)
)
+
1
0
dλ
φ
p−1
(λλ
)R(λ
)
'
. (9.3.52)
We substitute for the first two terms within the square brackets on the RHS of (9.3.52)
using the relation (9.3.48) and obtain
0 = qφ(λ)
⎡
⎣
−
1
1 − q
+ (1 −q)
∞
p=2
a
p
q
p−2
φ
p−2
(λ)
⎤
⎦
+
∞
p=2
a
p
q
p−1
&
( p − 1)
1
0
dλ
R(λ
)φ
p−2
(λ
)φ({λ
/λ}
sg(λ−λ
)
)
+
1
0
dλ
φ
p−1
(λλ
)R(λ
)
'
. (9.3.53)
The equation for the response function
From eqn. (9.3.15) for the response function R(t, t
) we obtain, on setting the LHS of this
equation to zero in the aging regime,
0 ≈
∂
∂t
R
A
(t, t
) =−z
∞
R
A
(t, t
) +
t
+δ
t
ds
A
(t, s)R
F
(s, t
)
+
t−δ
t
+δ
ds
A
(t, s)R
A
(s, t
) +
t
t
−δ
ds
F
(t, s)R
A
(s, t
). (9.3.54)
In writing the expression for the response function in the aging regime, we express the
RHS of the above equation in terms of integrals J
i
(i = 1,...,3) as
0 =−z
∞
t
−1
R(λ) + J
1
+ J
2
+ J
2
. (9.3.55)
We evaluate the integrals J
1
, J
2
, and J
3
in Appendix A9.2.2 and, using J
1
, J
2
, J
3
, and z
∞
in eqn. (9.3.55), we obtain the relation
0 = R(λ)
⎡
⎣
−z
∞
−
∞
p=2
a
p
#
( p − 1)q
p−2
φ
p−2
(λ)[q − 1]+[1 −q
p−1
]
$
⎤
⎦
+
∞
p=2
a
p
( p − 1)q
p−2
1
λ
dλ
λ
φ
p−2
(λ
)R(λ
)R(λ/λ
). (9.3.56)
9.3 A mean-field model 467
Now, using the relation (9.3.48) in the RHS of (9.3.57), we simplify it further to the form
0 = R(λ)
⎡
⎣
−
1
1 − q
+ (1 −q)
∞
p=2
a
p
( p − 1)q
p−2
φ
p−2
(λ)
⎤
⎦
+
∞
p=2
a
p
( p − 1)q
p−2
&
1
λ
dλ
λ
φ
p−2
(λ
)R(λ
)R(λ/λ
)
'
. (9.3.57)
We have now obtained from the above analysis eqns. (9.3.53) and (9.3.57) treating eqns.
(9.3.14) and (9.3.15), respectively, in the aging regime. These two relations between the
correlation and response functions in the aging regime should also be consistent with nec-
essary boundary conditions so as to match with the corresponding solutions in the FDT
regime. Therefore in the limit t → t
or λ →1wehaveφ(λ = 1) ∼ 1 and R(λ = 1) = 0.
Using these conditions and eqns. (9.3.53) and (9.3.57) in the limit λ →1, we obtain
q
⎡
⎣
−
1
1 − q
+ (1 −q)
∞
p=2
a
p
q
p−2
⎤
⎦
+
∞
p=2
a
p
pq
p−1
I
q
= 0, (9.3.58)
−
1
(1 − q)
2
+
∞
p=2
a
p
( p − 1)q
p−2
= 0. (9.3.59)
The dynamic-transition point and the corresponding NEP q are computed from the solution
of the equation
(1 − q)
−2
=
∞
p=2
a
p
( p − 1)q
p−2
. (9.3.60)
By substituting eqn. (9.3.59) into eqn. (9.3.58) we obtain
(1 − q)
∞
p=2
a
p
( p − 2)q
p−1
=
∞
p=2
a
p
pq
p−1
I
q
. (9.3.61)
To evaluate the integral I
q
on the RHS we need more information on the correlation and
response functions. The correlation and response functions in the aging regime are no
longer linked through the FDT. We consider here the modified relation (9.1.1) in terms of
a constant FDT-violation parameter m as
R
A
(t, t
) = m
∂
∂t
C
A
(t, t
). (9.3.62)
Using the solution (9.3.29) in the aging regime, the corresponding relation of the scaling
functions is obtained as
R(λ) = mq
∂
∂λ
φ(λ). (9.3.63)
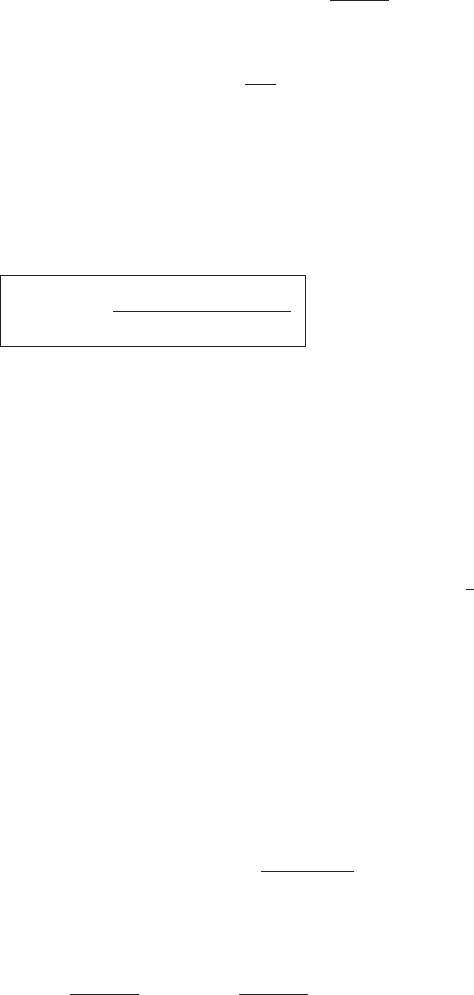
468 The nonequilibrium dynamics
Now we evaluate the RHS of (9.3.61) involving the integral I
q
,
∞
p=2
a
p
pq
p−1
I
q
= m
∞
p=2
a
p
pq
p
1
0
dλ
φ
p−1
(λ
)
dφ(λ
)
dλ
= m
∞
p=2
a
p
q
p
1
0
dλ
d
dλ
φ
p
(λ
)
*
*
*
*
1
0
= m
∞
p=2
a
p
q
p
. (9.3.64)
Therefore we obtain from eqn. (9.3.61) the following expression for the FDT-violation
parameter m:
m = (1 −q)
5
∞
p=2
a
p
q
p−2
( p − 2)
5
∞
p=2
a
p
q
p−1
. (9.3.65)
Let us now consider two special cases.
(a) Case I Here we include only the quadratic term in the expression for the memory
kernel containing only the p = 3 term, i.e., (t, t
) = a
3
C
2
(t, t
). In this case we have
the following two equations for q and m:
(1 − q)
−2
= 2a
3
q, (9.3.66)
m = q
−1
− 1. (9.3.67)
For the state in which the FDT is satisfied we have m = 1 and hence q =
1
2
and
a
3
= 4. The coupling-constant value a
3
= 4 marks the transition to the nonergodic
state. Note that for this case we have, from (9.3.48) and (9.3.38), that the constant
˜z
∞
= 0, rendering eqn. (9.3.47) in the FDT regime the same as that in the schematic
model of a structural glass.
(b) Case II We consider the situation in which the kernel includes the p = 2and3terms
in the expansion
(t, t
) = a
2
C(t, t
) + a
3
C
2
(t, t
). (9.3.68)
The two equations involving a
2
and a
3
are obtained as
(1 − q)
−2
= a
2
+ 2a
3
q, m =
a
3
q(1 − q)
a
2
q + a
3
q
2
. (9.3.69)
For the ergodic state in which the FDT is satisfied, i.e., m = 1, the above two equations
for a
2
and a
3
are solved to obtain
a
2
=
1 − 2q
(1 − q)
2
, a
3
=
1
(1 − q)
2
.

9.3 A mean-field model 469
On eliminating q from the above relation we obtain the following line of dynamic
transition:
a
2
= 2
√
a
3
− a
3
. (9.3.70)
In the equilibrium limit this model is identical to what is termed the φ
12
model in the
literature and gives rise to the stretched-exponential relaxation. The relaxation behav-
ior for the equilibrium correlation function for this model has been discussed in detail
in Chapter 8. Numerical solution of eqns. (9.3.14) and (9.3.15) (Singh and Das, 2010,
unpublished) gives the correlation and response functions, respectively, in the nonequi-
librium states. The different stages of the dynamics as depicted in the above analysis
are displayed in Fig. 9.9 in a form similar to the corresponding results from computer
simulations shown in Fig. 9.5.
9.3.4 Quasi-ergodic behavior
Let us consider the behavior of the correlation and response functions in the two regimes
which emerges from the above analysis. First, within the FDT regime the behavior follows
the typical mode-coupling equation given by (9.3.47). The solution for the correlation
function as discussed in the previous chapter is of the form
10
–3
10
0
10
3
10
6
t
0.0
0.5
1.0
0.0
0.5
1.0
C
0.0
0.5
-M
Fig. 9.9 Results from the theoretical model with the kernel given by eqn. (9.3.68), showing the
quantity [1 − C
k
(t)]/T involving the correlation function (solid line) and the integrated response
function −M
k
(t) (dashed line) vs. time t. The parameter values are a
2
= 0.5anda
3
= 6.0. The two
curves overlap when the FDT is satisfied for small t and for larger values of the correlation functions.
This is qualitatively similar to the simulation results displayed in Fig. 9.4. The two curves become
identical in equilibrium and the corresponding solution is shown with the dot–dashed line (Singh and
Das, 2010, unpublished).

470 The nonequilibrium dynamics
C
F
(t, t
) ≡ C
F
(t − t
) = q + B
1
τ
−a
+···. (9.3.71)
The correlation function decays over the time scale of the FDT regime to the plateau value
given by the nonergodicity parameter q. On the other hand, within the aging regime the
scaling form for the correlation function follows C(t, t
) ∼ qφ(λ), where λ = h(t
)/ h(t).
For τ = t −t
small compared with t , this result is expressed in terms of a Taylor expansion
around λ = 1as
C(t, t
) ≡ qφ(λ) = q +
i
A
i
(1 − λ)
i
= q − A
1
{τκ(t)}+···. (9.3.72)
By expanding λ ≡ h(t
)/ h(t) around λ = 1(t = t
) we obtain κ(t) as
κ(t) =
d ln h(t)
dt
. (9.3.73)
κ(t) ∼t
−1
corresponds to the case of simple aging, i.e., h(t ) ∼t
γ
with exponent γ .
However, a more general form of the asymptotic dynamics is envisaged with the choice
κ(t) =t
−μ
, which gives for the aging function h(t) the result
h(t) = exp
t
1−μ
1 − μ
, (9.3.74)
the corresponding integration constant being chosen to be unity. The case of μ = 0
corresponds to the case h(t) ∼ exp(t) and hence h(t + t
w
)/ h(t
w
) ∼ exp(t), implying
time-translational invariance of the correlation function. On the other hand, μ = 1 cor-
responds to h(t) ∼ t, which is termed simple aging (h(t + t
w
)/ h(t
w
) ∼ f (t/t
w
). Thus,
the sub-aging behavior will give 0 <μ<1. Numerical solutions of eqns. (9.3.14) and
(9.3.15) were obtained by Kim and Latz (2003) for the p = 3 case in which the memory
functions are given by eqns. (9.3.18) and (9.3.19) with μ = pβ
2
/2(β = 1/k
B
T is the
inverse temperature). For T = 0.61 the numerical solution conforms to the above empiri-
cal form of h(t) with μ = 0.82. For lower temperatures the exponent μ becomes larger to
make the data for correlation and response functions collapse on a single curve.
The behavior of the correlation function over the intermediate time scales is obtained by
matching the solutions in the FDT regime and the aging regime. Let there be a crossover
time scale t
δ
expressed in terms of the exponent δ (δ<1). Over this time the nature of
the correlation function changes from the FDT behavior (9.3.71) to the form given by
(9.3.72). For large enough τ ∼O(t) the decay crosses over to the aging behavior. The
above two forms are similar to the power-law relaxation of equilibrium correlation func-
tions discussed in the previous chapter. The von Schweidler-like exponent b is unity in this
case. For the plateau region the solution is written in a general form in terms of the scaling
functions g
i
as
C(t, t
) = C(t − t
) = q + g
1
(τ/t
δ
)t
−α
+···. (9.3.75)
The correlation function (9.3.75) reduces to the above two behaviors, respectively given
by (9.3.71) and (9.3.72), in two limiting cases. In the FDT limit, matching (9.3.75) with
