Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond
Подождите немного. Документ загружается.


9.2 The effective temperature 451
9.2.1 The phenomenological approach
The nonequilibrium state of the supercooled liquid in the glass-transition region (near the
calorimetric glass-transition temperature T
g
) has time scales of relaxation that are much
larger than the laboratory time scales. The nonequilibrium liquid is in a frozen state that
is characterized in terms of a time-dependent fictive temperature T
fic
. The nature of this
dependence for the fictive temperature is defined from a phenomenological approach. In
the limiting case of equilibrium liquid at high temperature the time dependence is absent
and T
fic
= T . Near the glass-transition range generally T
fic
> T . The time dependence of
T
fic
is prescribed in terms of the nonlinear differential equation
dT
fic
dt
=−
T
fic
− T
τ(T, T
fic
)
. (9.2.2)
The time τ(T, T
fic
) depends self-consistently on the fictive temperature T
fic
(t) itself, as
well as on the temperature of the bath T . The resulting T
fic
(t) is obtained by making some
suitable phenomenological choices for τ(T , T
fic
) in eqn. (9.2.2). An example (Tool, 1946;
Gardon and Narayanaswamy, 1970; Narayanaswamy, 1971; Moynihan et al., 1976; Jäckle,
1986)is
τ(T, T
fic
) = τ
0
exp
xA
T
+
(1 − x) A
T
fic
, (9.2.3)
where the parameter x ∈[0, 1]. A and τ
0
are constants related to the dynamics of the sys-
tem. For very low temperatures T
fic
→T
g
. This time-dependent fictive temperature there-
fore follows from a purely phenomenological basis.
9.2.2 A simple thermometer
Here some generic property of the nonequilibrium state, e.g., violation of the fluctuation–
dissipation theorem (FDT), is used in extending the usual thermodynamic description of
the equilibrium state to systems that are out of equilibrium. Let us consider the most typical
thermodynamic property, namely the “temperature” of the nonequilibrium system. We note
that in equilibrium the temperature is measured with some auxiliary device (thermometer)
linked to the original system in a state of equilibrium. The measurement of the “tempera-
ture” of the system is then done in terms of the properties of the “contents” of the device.
Similarly, for the nonequilibrium system the measuring device or “thermometer” couples
to some observable O (say) of the system. A crucial step for describing the nonequilibrium
state involves the extension of the equipartition law of equilibrium statistical mechanics to
the out-of-equilibrium state of the thermometer. The average kinetic or potential energy per
degree of freedom for the thermometer is equal to (k
B
T
eff
)/2, where T
eff
is the effective
temperature of the system. The underlying assumption here in extending the thermody-
namic concept of temperature, of course, is that the system has reached a state in which the
flow of heat is very small. We demonstrate below that the effective temperature T
eff
of the
nonequilibrium state defined in this manner is linked to the fluctuations and responses of

452 The nonequilibrium dynamics
the observable(s) O of the nonequilibrium system (Cugliandolo et al., 1997a; Cugliandolo,
2003). In equilibrium these are related through the FDT. Thus the effective temperature in
the equilibrium limit reduces to the bath temperature. For the out-of-equilibrium case this
is closely linked to the FDT-violation factor.
The measurement of the effective temperature T
eff
requires a device (thermometer)
whose characteristic time scale matches with that of T
eff
. The simplest example of such
a device we consider is a harmonic oscillator with characteristic oscillation frequency ω
0
.
It measures the temperature of a nonequilibrium system S by coupling to an observable
denoted by O, and the system is kept in contact with a heat bath at temperature T .IfS is
in equilibrium at temperature T , then the energy of the oscillator will satisfy E
osc
=k
B
T
(Cohen-Tannoudji et al., 1977). The Hamiltonian for the system plus the thermometer is
obtained as
H
tot
= H(S) + H
osc
+ H
int
, (9.2.4)
where the energy of the oscillator is
H
osc
=
˙x
2
2
+
ω
2
0
x
2
2
. (9.2.5)
Assuming linear coupling, we obtain for the interaction part
H
int
=−εOx. (9.2.6)
The oscillator’s equation of motion is given in terms of the characteristic frequency,
¨x =−ω
2
0
x + εO(t). (9.2.7)
Assuming that εx(t) is small, the effect of the thermometer (oscillator) on the observable
O is computed from the linear response theory. Let us assume that the fluctuating part of
the observable O in the off-equilibrium system is denoted by
˜
O. The observable O(t) is
therefore obtained as
O(t) =
˜
O(t) +ε
t
0
dt
R
O
(t, t
)x(t
), (9.2.8)
where the response function R
O
for the observable O is defined as
R
O
(t, t
) =
δ
δ{εx(t
)}
O(t ). (9.2.9)
The angular brackets represent the average over the fluctuations. The correlation function
for the observable O (in the absence of the coupling to the oscillator) is defined as
C
O
(t, t
) =
˜
O(t)
˜
O(t
). (9.2.10)
Using the relation (9.2.8) in eqn. (9.2.7), we obtain the following fluctuating equation for
the oscillator variable x(t):
¨x − ε
2
t
0
dt
R
O
(t, t
)x(t
) + ω
2
0
x(t) = ε
˜
O(t). (9.2.11)

9.2 The effective temperature 453
The above equation of motion for the oscillator indicates that it takes up energy through
fluctuations of
˜
O and dissipates through the response of the system. We solve eqn. (9.2.11)
in Appendix A9.1 to obtain the average mean-square displacement after a time t
w
that is
much larger than the characteristic time scale ω
−1
0
of the oscillator. The average potential
energy of the oscillator coupling to the system through the observable O, measured at time
t
w
, is given by
ω
2
0
2
x
2
t
w
=
ω
0
C
O
(ω
0
, t
w
)
2χ
(ω
0
, t
w
)
, (9.2.12)
where have we defined
C
O
(ω, t) = Re
t
0
dt
C
O
(t, t
)e
−ω(t−t
)
, (9.2.13)
χ
(ω, t) = Im
t
0
dt
R(t, t
)e
−ω(t−t
)
. (9.2.14)
The effective temperature defined above is analogous to the kinetic temperature of the
system and is obtained by equating the average potential energy to k
B
/2 times the “tem-
perature” T
O
(ω
0
, t
w
) of the out-of-equilibrium system. Thus we obtain the result
T
O
(ω
0
, t
w
) =
ω
0
C
O
(ω
0
, t
w
)
χ
(ω
0
, t
w
)
(9.2.15)
defining the temperature in units of k
B
. The above example of the thermometer being iden-
tified with a single oscillator can easily be generalized to a more general measuring device
(Cugliandolo et al., 1997b). The effective temperature obtained above is thus dependent on
(a) the waiting time t
w
at which the temperature is being measured,
(b) the characteristic frequency (ω
0
) or time
ω
−1
0
of the thermometer, and
(c) the observable O of the system to which the thermometer is coupled.
In equilibrium the effective temperature is independent of all of the above three quantities
and becomes equal to the thermodynamic temperature of the bath. The above expression
for the effective temperature also shows that it is compatible with the Fourier-transformed
expression for the FDT-violation parameter X (C), assuming that it does not vary too
fast with ω
0
. The latter condition is generally satisfied in systems with slow dynamics
(Cugliandolo et al., 1997b). From the MD studies of FDT violation (Kob and Barrat, 1997)
discussed above, the effective temperature has been obtained for the BMLJ mixture after an
initial quench. The effective temperature was studied in a laboratory glass-forming system,
glycerol, by Grigera and Israeloff (1999), who did an experiment similar to the oscillator
model described above. These authors studied the FDT below the glass-transition temper-
ature T
g
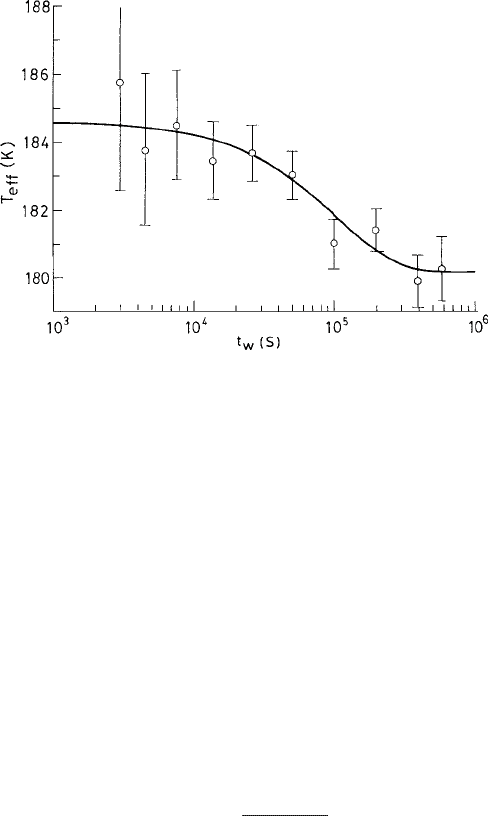
by measuring the dielectric susceptibility and the noise correlations. Figure 9.6
displays the effective temperature T
eff
of glycerol following a quench to T =179.8K
against the corresponding waiting time t
w
. T
eff
relaxes to T on a time scale that is compa-
rable to that for the aging of the susceptibility as seen in the experiment.
454 The nonequilibrium dynamics
Fig. 9.6 The effective temperature of glycerol T
eff
(see the text) vs. the waiting time t
w
following
a quench to T =179.8 K. The points display the experimental data while the solid line presents the
exponential decay to the equilibrium temperature. Reproduced from Grigera and Israeloff (1999).
c
American Physical Society.
We have considered above the case for the nonequilibrium state with relaxational
dynamics. As already indicated, the out-of-equilibrium situation can also be created by
applying a steady-state perturbation to the system, e.g., applying a homogeneous steady
shear flow (Berthier and Barrat, 2002). The steady shear flow is characterized by the corre-
sponding shear rate γ
0
, which creates a nonequilibrium steady state with time translational
invariance. The inverse of the shear rate γ
−1
0
introduces a time scale and acts as a control
parameter in studying the nonequilibrium state, similarly to the waiting time t
w
in relax-
ational dynamics. In this case a simple harmonic oscillator is used as a thermometer by
coupling it to the system through the observable O. This analysis gives rise to the def-
inition of an effective temperature T
O
(ω
0
) for the liquid in the steady state (with time
translational invariance),
T
O
(ω
0
) =
ω
0
C
O
(ω
0
)
χ
(ω
0
)
, (9.2.16)
where we have used the definitions
C
O
(ω) = Re
∞
0
dt C
O
(t)e
ωt
, (9.2.17)
χ
(ω) = Im
∞
0
dt R(t)e
ωt
. (9.2.18)
To test the above idea of effective temperature being measured with an oscillator, Berthier
and Barrat (2002) simulated an 80 : 20 mixture of N = 2916 Lennard-Jones particles of
types A and B with the same interaction as that described in Section 4.3.1. Lees–Edwards
9.2 The effective temperature 455
boundary conditions are used in a cubic simulation box of size L = 13.4 in units of the
length σ
AA
defined by the Lennard-Jones interaction potential. The liquid is in a state of
steady shear with γ
0
= 10
−3
and in contact with a heat bath at temperature T = 0.3.
The units of time and temperature are as defined for the binary Lennard-Jones mixture
in Chapter 1. The simulated mixture includes 10 massive tracer particles, whose masses
are given by m
tr
∈[1, 10
7
]. They are otherwise identical to the particles of type A. The
equilibrium structure of the simulated system is the same as that of the system with normal
“light” particles. The Einstein frequency ω
E
of the tracer particles is defined by
ω
E
=
n
0
3m
tr
dr g(r)∇
2
U (r)
1/2
, (9.2.19)
where g(r) is the pair correlation function and U (r) represents the interaction potential
between the particles. ω
E
characterizes the oscillation frequency for a fluid particle in
the cage formed by its neighbors. From eqn. (9.2.19) it follows that the corresponding
oscillation frequency falls by three orders of magnitude for the most massive tracer particle.
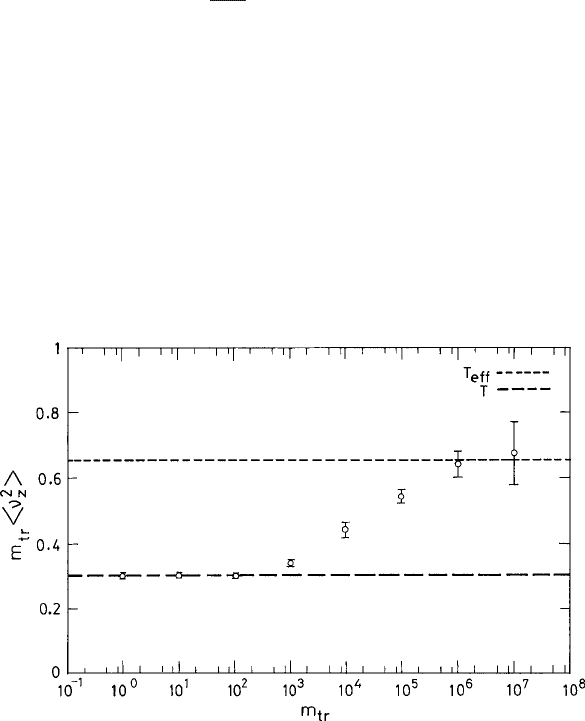
Berthier and Barrat computed the effective temperature from the average kinetic energy
or the average mean-square velocity in the direction transverse to the flow of the tracer
particles. In Fig. 9.7 the plot of m
tr
1
v
2
z
2
≡ T
eff
vs. the mass m
tr
shows how the effec-
tive temperature varies with the mass of the tracer particles. While for the light particles
the effective temperature is the same as that of the bath (T = 0.3 in this simulation), it
crosses over to T
eff
= 0.65 for the heaviest particles. The dynamics of the tracer particles
Fig. 9.7 The mean kinetic energy in the z direction vs. the mass m
tr
(m
tr
∈[1, 10
7
]) of the tracer
particle in a BMLJ system for T
f
=0.3 and shear rate γ =10
−3
. The horizontal lines are for
T =0.3andT
eff
=0.65. Reproduced from Berthier and Barrat (2002).
c
American Institute of
Physics.
456 The nonequilibrium dynamics
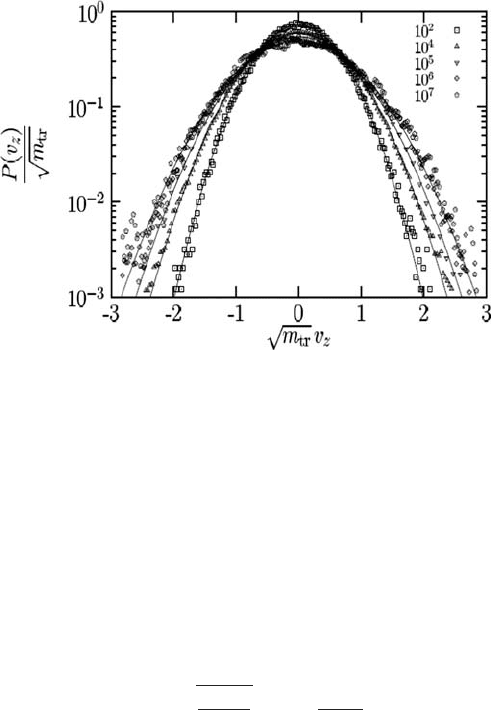
Fig. 9.8 The probability distribution function P(v
z
) of the velocity v
z
for various massive tracers
(m
tr
∈[1, 10
7
] as shown on the figure) of type A in the BMLJ system. Plots of P(v
z
) for dif-
ferent tracer particles follow Gaussian shapes (shown with full lines) with corresponding effective
temperatures. For m
tr
=10
2
, T
eff
=0.3 (the equilibrium case); for m
tr
=10
4
–10
5
, T
eff
=0.44–0.54
(the crossover region); and for m
tr
=10
6
–10
7
, T
eff
=0.65 (the asymptotic effective temperature).
Reproduced from Berthier and Barrat (2002).
c
American Institute of Physics.
represents a low-frequency filter coupled to fluctuations in the host fluid. Hence they act as
thermometers measuring the corresponding effective temperatures in the nonequilibrium
steady state over the characteristic time scales (determined by the corresponding inverse
frequencies) of the respective tracer particles. In Fig. 9.8 it is shown that the probability
distribution of the velocity P(v
z
) follows a Gaussian form,
P(v
z
) =
9
m
tr
2π T
eff
exp
−
m
tr
v
2
z
2T
eff
, (9.2.20)
which implies a Maxwellian distribution form with T
eff
replacing the temperature.
9.3 A mean-field model
In this section we consider a theoretical model for the slow dynamics in the nonequilibrium
state. The mean-field theory considered here reduces in the equilibrium limit to a form
very similar to the mode-coupling model discussed in the previous chapter. So far in our
discussion of the mode-coupling theory we have assumed that time translational invariance
(TTI) holds in the supercooled liquid state, i.e., the correlation of the fluctuations at times
t and t
depends only on the difference t − t
of the two times. However, in the case of
glassy relaxation, when the supercooled liquid is out of equilibrium, the TTI property does
not hold. To be more specific, the dynamic correlation C(t, t
) between two times depends
both on t and on t
and is not a function of t − t
only. We consider here the mean-field

9.3 A mean-field model 457
dynamics of the spherical p-spin model in a situation in which TTI does not hold. The time
evolution of the p-spin spherical model is given by the dissipative Langevin equation,
−1
0
∂
∂t
σ
i
(t) = z(t)σ
i
(t) −
δ H
δσ
i
(t)
+ ς
i
(t), (9.3.1)
where
−1
0
is a bare kinetic coefficient. Here z(t) is the Lagrange multiplier which ensures
the spherical constraint on the spins {σ
i
},
1
N
N
i=1
σ
2
i
= 1. (9.3.2)
To reach the dynamical equations for the correlation function averaged over the noise ς
i
,
in a situation in which TTI does not hold, we start from the Schwinger–Dyson equation,
G
−1
0
(1, 2) = G
−1
(1, 2) −
A
(1, 2). (9.3.3)
In the MSR formalism G has elements corresponding to a set of slow variables {ψ
α
} (to
be denoted as α) as well as a conjugate set of hatted fields {
ˆ
ψ
α
} (to be denoted as ˆα). The
matrix structure of this equation contains both the correlation and the response functions
as elements of the matrix G. An important property of this matrix is that the elements of
its inverse, i.e., G
−1
ψψ
, with both the indices as unhatted fields must be zero. This is required
by the structure of the MSR field theory. See the text given above eqn. (7.2.31) for proof
of this. Then
[G
−1
]
αα
=. (9.3.4)
Hence the inverse of the full matrix G
−1
takes the form
G
−1
≡
⎡
⎢
⎣
[R
−1
0
− ]
α
ˆ
β
[R
−1
0
− ]
ˆαβ
−
˜
ˆα
ˆ
β
⎤
⎥
⎦
. (9.3.5)
In writing the above expression for G
−1
, we denote the elements of the self-energy matrix
corresponding to the response functions, i.e., with the matrix indices being hatted–unhatted
(i.e., ψ
ˆ
ψ) fields, by and the elements of the G
−1
matrix between hatted fields (i.e.,
ˆ
ψ
ˆ
ψ)
by . Considering the general form of the MSR action (see eqn. (8.4.22)) and taking into
account the Gaussian random nature of the noise terms whose correlations are expressed
in terms of the bare transport coefficients
0
αβ
, we obtain for
˜
on the RHS of (9.3.5)
˜
ˆα
ˆ
β
(t, t
) = 2
0
αβ
δ(t − t
) +
ˆα
ˆ
β
(t, t
). (9.3.6)
The explicit form of the operator R
−1
0
in the case of the p-spin model is obtained from the
linear part of the equation of motion (9.3.1) for a single-spin variable σ as
R
−1
0
≡
∂
∂t
+ z(t)
. (9.3.7)
458 The nonequilibrium dynamics
On taking the inverse of the above matrix to obtain G we have
G ≡
⎡
⎢
⎣
R
α ˆν
˜
ˆν
ˆ
δ
R
ˆ
δ
β
R
α
ˆ
β
R
ˆαβ
⎤
⎥
⎦
, (9.3.8)
where we write
˜
in terms of the single ˆσ ˆσ element of the self-energy matrix as
˜
(t, t
) = 2δ(t − t
) + (t, t
), (9.3.9)
with time being rescaled with the bare transport coefficient
0
. Therefore the correlation
of the hatted fields G
ˆ
ψ
ˆ
ψ
remains equal to zero (Martin et al., 1973; Kirkpatrick and Thiru-
malai, 1987a) in order to maintain causality. For the correlation function elements we
obtain the relation
C = R
˜
R. (9.3.10)
On applying the operator R to the Schwinger–Dyson equation for the response elements
we obtain
R
−1
0
R = δ(t − t
) + R. (9.3.11)
For the correlation function matrix C we obtain from eqn. (9.3.10)
R
−1
C =
˜
R. (9.3.12)
Now, on replacing R
−1
= R
−1
0
− using the Schwinger–Dyson equation, we obtain
R
−1
0
C =
˜
R +C. (9.3.13)
From eqns. (9.3.13) and (9.3.11), respectively, we obtain the following equations for the
dynamics of the correlation and the response functions between times t and t
:
∂
∂t
C(t, t
) =−z(t)C(t, t
) + 2R(t
, t) +
t
0
dt
(t, t
)R(t
, t
)
+
t
0
dt
(t, t
)C(t
, t
), (9.3.14)
∂
∂t
R(t, t
) =−z(t)R(t, t
) + δ(t − t
) +
t
t
dt
(t, t
)R(t
, t
). (9.3.15)
For the sake of definiteness we take t > t
. The fact that the time-ordered property of the
response function, i.e., R(t, t
), is zero for t < t
due to causality has been used in writing
eqns. (9.3.14) and (9.3.15). The nonequilibrium dynamics for all times t and t
are thus
given by the first-order integro-differential equations which admit a unique solution for
finite times. At equal times the conditions maintained are
C(t, t) = 1, R(t, t
−
) = 1, (9.3.16)
∂
∂t
C(t, t
±
) =±1. (9.3.17)
9.3 A mean-field model 459
The spherical constraint and the boundary conditions at t = t
require that the Lagrange
multiplier z(t) is determined in terms of the kernel functions. We apply eqn. (9.3.14) for
the case t
= t
+
and obtain, using the above boundary conditions (9.3.16),
z(t) = 1 +
t
0
ds
!
(t, s)R(t
+
, s) + (t, s)C(t
+
, s)
"
. (9.3.18)
We have not specified yet the form of the self-energy matrices or the kernels and
which represent the effect of nonlinearities in the equations of motion. Further discussion
of the dynamics requires specification of these kernels.
9.3.1 The mode-coupling approximation
In our discussion so far we have absorbed all the effects of the nonlinearities into the self-
energy matrix elements and .Forthep-spin Hamiltonian (8.4.2) discussed in Chapter
8, the kernels and are obtained as
(t, t
) = μ( p − 1)C
p−2
(t, t
)R(t, t
),
(t, t
) = μC
p−1
(t, t
), (9.3.19)
where μ = pβ
2
/2 with β = 1/T the inverse temperature. For subsequent treatment of
the nonequilibrium discussion we generalize the expressions (9.3.19) for the self-energy or
the memory-kernel matrix elements (which are consequences of the nonlinear dynamics)
to the following general forms involving polynomials expressed in terms of a series of
coupling constants {a
p
}:
(t, t
) =
∞
p=2
a
p
( p − 1)C
p−2
(t, t
)R(t, t
),
(t, t
) =
∞
p=2
a
p
C
p−1
(t, t
). (9.3.20)
The above polynomial form for the memory functions in the context of MCT of liquids
was proposed by Das et al. (1985a). It has very often been used in the mode-coupling
literature with respect to schematic models (Götze, 1991). Recently, such forms for mem-
ory kernels have also been argued (Singh and Das, 2009) to apply for amorphous solids,
on treating individual particle displacements as soft spins. We use this general form for the
memory function for discussion of the asymptotic dynamics here. This approach of writing
the kernel functions and as functionals of the correlation and response functions con-
stitutes the basic ingredient of the mode-coupling approximation. It has also been argued
(Bouchaud et al., 1996) that, in systems where the force term in the Langevin equation
of the slow modes is obtained from a potential and detailed balance holds, the following
relation holds:
(t, t
) =
[C(t, t
)]R(t, t
), (9.3.21)

460 The nonequilibrium dynamics
with
(x) = d(x)/dx. For systems in which the equality (9.3.21) does not hold, there
is violation of the detailed balance. The mode-coupling dynamics with kernels satisfying a
modified version of eqn. (9.3.21) in the simple form (with a parameter ¯μ)
(t, t
) =¯μ
[C(t, t
)]R(t, t
) (9.3.22)
has been taken (Cugliandolo et al., 1997a) to describe driven systems.
The asymptotic dynamics for both t and t
large is obtained from the solution of the
differential equations (9.3.15) and (9.3.14). The solutions of these equations are obtained
(Cugliandolo and Kurchan, 1993) in analytic form for the following two broad regimes.
A crucial factor driving the nonequilibrium dynamics comes from z(t), which is explicitly
time-dependent.
A. Both t and t
are large such that (t − t
)/t → 0. Over this time scale the differ-
ence between the two time arguments in the two-point correlation functions is small
and translational invariance is satisfied. This is the region in which the fluctuation–
dissipation theorem (FDT) holds, and will be referred to as the FDT regime.
B. Both t and t
are large such that (t − t
)/t ∼ O(1). Over this time scale the differ-
ence between the two time arguments in the two-point correlation functions is large
and nonequilibrium dynamics does not obey time translational invariance. This will be
referred to as the aging regime.
We discuss the dynamics in these two regimes below.
9.3.2 The FDT regime
In the FDT regime, the correlation function C(t, s) and the response function R(t, s) are
only functions of the difference of the two times (t − s) as a result of time translational
invariance (TTI). Let these be denoted by C
F
and R
F
, respectively, being related through
the FDT expression
R
F
(t − s) = (t − s)∂
s
C
F
(t − s), (9.3.23)
where ∂
s
denotes the derivative with respect to s and we have absorbed the k
B
T factor
into the definition of the correlation function. In this case, it follows directly from the
expressions (9.3.20) for the memory functions that the corresponding TTI quantities are
related:
F
(t − t
) =
∂
∂t
F
(t − t
). (9.3.24)
In the following we will show that eqns. (9.3.14) and (9.3.15) for the correlation and
response functions, respectively, reduce to a single equation for their corresponding TTI
counterparts C
F
and R
F
. Let us consider the equation for the correlation function (9.3.14).
The two integrals on the RHS are rearranged to write the equation in the form
