Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

8.2 Evidence from experiments 401

Table 8.1 A list of T

and the corresponding T

in degrees

Kelvin for some commonly studied glass-forming materials.

Material T

CKN 483 378 333 1.1

PC 218 190 160 1.2

OTP 329 290 243 1.2

Salol 315 263 218 1.2

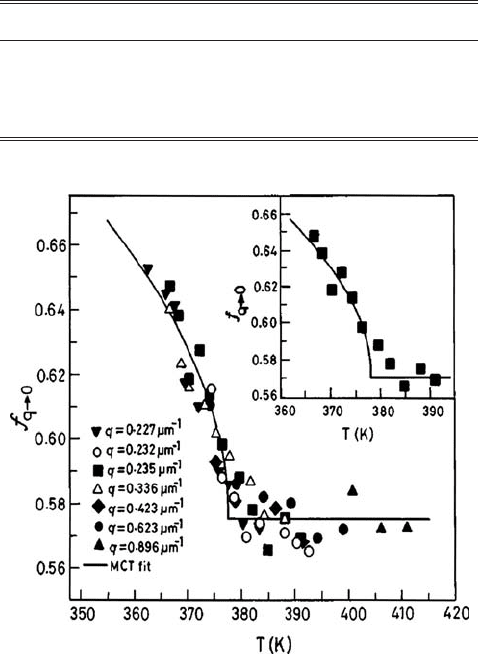
Fig. 8.5 The effective Debye–Waller factor for CKN vs. temperature T at q =0. The q =0value

is obtained from the corresponding results at different q values measured with impulsive light-

scattering spectroscopy. The curves are ﬁts to the square-root cusp. Reproduced from Yang and

Nelson (1996).

 American Institute of Physics.

delta function π f

δ(ω) to the dynamic structure factor at densities beyond the dynamic

transition point. In reality, however, the NEP is determined from the area under the α-peak

having ﬁnite width. If the correlation function is obtained with respect to time, the NEP

is approximated by the plateau value of the density correlation function or the tagged-

particle correlation function, for f

and f

, respectively. By projecting the temperature

dependence of the NEP into a cusp-like behavior, the mode-coupling transition tempera-

ture T

is identiﬁed. The elastic modulus measured in the impulsive stimulated scattering

of light from different wave vectors q (Yang and Nelson, 1996) is converted to obtain NEPs

at q =0 relating to density ﬂuctuations for macroscopic wavelengths. In Fig. 8.5, a plot of

402 The ergodic–nonergodic transition

the effective Debye–Waller factor vs. temperature T is shown for CKN (0.4Ca(NO

)

–

0.6KNOB

) at q =0. The critical temperature estimated is T

=378 ± 2K. InTable 8.1,

the mode-coupling temperature T

and the corresponding T

for a few commonly studied

materials are listed. The cusp behavior was similarly analyzed to identify T

in other mate-

rials listed in Table 8.1: o-terphenyl (OTP) (Tölle et al., 1997), CKN (Kartini et al., 1996;

Pimenov et al., 1996), salol (Toulouse et al., 1993; Yang and Nelson, 1995), and propy-

lene carbonate (PC) (Yang et al., 1996). The relative change of the NEP in the asymptotic

range where the cusp behavior dominates is not very large and hence the identiﬁcation of

tracing a cusp-like behavior (see the inset of Fig. 8.5) in the NEP is somewhat arbitrary.

Power-law relaxations

1. The critical decay: The decay (t/τ

)

−a

given by eqn. (8.1.47) has been observed in

several systems beyond microscopic time scales. The dielectric-loss data for the molten

salt CRN (0.4Ca(NO

)

–0.6RbNO

) show such a decay with an exponent a =0.20

over three decades in time (Lunkenheimer et al., 1997b). The NEP f , the amplitude

of the power law h, and the time τ

are treated here as ﬁtting parameters. This critical

power-law type relaxation is expected only over a limited time or frequency window

where the correction terms indicated in eqn. (8.1.53) can be neglected. However, direct

numerical solution of the MCT equations for a one-component Lennard-Jones system

(Smolej and Hahn, 1993) indicates that the critical decay is observed for a relative

distance from the dynamic transition (in terms of density) of  ≈ 4.2 ×10

−4

only.

2. Von Schweidler (VS) relaxation. Like the critical decay described above, identiﬁcation

of this second power-law regime is also problematic due to several factors. For times

t that are not long enough, the correlation function is above the critical plateau value,

merging the VS relaxation (8.1.48) with the critical decay (8.1.47). On the other hand,

higher-order corrections dominate at long times. Even the choice of the plateau is also,

in many cases, a bit arbitrary. The critical decay is observed only in the close vicinity

of the transition, while the range of validity of the VS relaxation is not known a priori,

thus making their observation rather subtle.

Owing to problems with the direct ﬁt of the time correlation-function data, it is some-

times convenient to do the data analysis for identifying the power-law behaviors in terms

of the frequency-dependent (dynamic) susceptibility function. The susceptibility function

is deﬁned in terms of the Laplace-transformed quantity

χ(z) = φ(t = 0) + zφ(z). (8.2.1)

The corresponding Fourier-transformed function is given by the imaginary part χ



.The

two power-law decays of t

−a

and t

in the time correlation function give rise to corre-

sponding frequency dependences in χ



of the form ω

and ω

−b

, respectively. As a result

of these two opposite trends, χ



reaches a minimum at an intermediate frequency ω =ω

min

In the region of this minimum the susceptibility function is interpolated with the schematic

form

8.2 Evidence from experiments 403



(ω) =



min

a + b





min



+ a



min





. (8.2.2)

The frequency corresponding to the susceptibility minimum ω

min

is inversely proportional

to the β-process time scale τ

, i.e., to 

1/(2a)

. Therefore the plot of (ω

min

)

vs. the cor-

responding temperature T of the liquid is expected to follow a straight line extrapolating

to meet the temperature axis at the dynamic transition point T

. The susceptibilities for

CKN at temperatures in the range T =468–383 K ﬁt well (Li et al., 1992) with the scal-

ing function for λ =0.81. This choice of λ corresponds to power-law exponents a =0.27

and b =0.46, respectively. In comparison, the susceptibility curves from the dielectric-loss

spectra (Lunkenheimer et al., 1997b) of CKN exhibit the minimum for T ≤ 417 K with

the master function corresponding to a somewhat lower value of λ =0.76. In general, the

range of validity of the scaling behavior over the time or the frequency scale increases as

the temperature T of the system approaches T

from above.

Similarly to the behavior ω

min

∼ τ

−1

∝|

1/(2a)

for the minimum of the susceptibil-

ity function, the position of the α-relaxation peak of the susceptibility function at ω

also

corresponds to the time scale τ

and ω

∼ τ

−1

∝|

, where γ =1/(2a) + 1/(2b).

Furthermore, the intensity χ



min

is proportional to

√



. Therefore plots of ω

, ω

1/γ





min



with temperature T should follow a straight line and meet the T axis on extrapola-

tion at T =T

(

=0) (Götze and Sjögren, 1992). This analysis is suitable for estimating

from the high-temperature side. This was applied to dielectric-loss spectra for CKN

(Lunkenheimer et al., 1997b). The exponents a and γ were used as ﬁtting parameters.

Figure 8.6 shows this estimation of T

for CKN and CRN, which was done by plotting

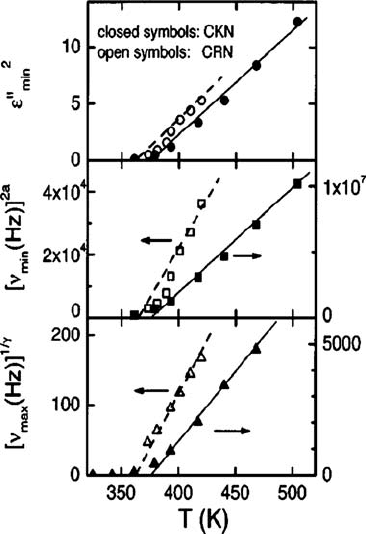
the temperature dependence of, respectively, from the top panel down, the height, the

position of the dielectric-loss minimum, and the α-peak position for CKN (closed sym-

bols) and CRN (open symbols). The best-ﬁt results a =0.30 and γ =2.6 were obtained

for CKN (corresponding to exponent parameter λ =0.76). The transition temperature T

for CKN obtained by extrapolating the dielectric-loss data is close to 375 K. This is com-

parable to the corresponding result T

=378 ± 2 K obtained by studying the location of

the square-root cusp as given by eqn. (8.1.24) or eqn. (8.1.40) for the NEP from the low-

temperature side. Similar ﬁts with ω

min

extracted from light-scattering data (Li et al., 1992)

for CKN give a =0.28 and γ =2.9, corresponding to λ =0.81, roughly in agreement with

the above dielectric-spectroscopy results. For CRN these exponent values are respectively

a =0.20 and γ =4.3 (corresponding to λ =0.91) and the estimate for T

lies between

360 K and 375 K.

Consider the case of another typical glass-forming material, propylene carbonate (PC).

Schneider et al. (1999) studied this material both in the normal and in the supercooled state

using dielectric spectroscopy over more than 18 decades of frequency. Analysis done with

the minimum of the dielectric-susceptibility data as well as the α-relaxation time scales

gives T

=187 K. The minimum in the dielectric-susceptibility function is described with

the scaling form (8.2.2) corresponding to a =0.29 and b =0.50 and is consistent with the

404 The ergodic–nonergodic transition

Fig. 8.6 Identiﬁcation of the mode-coupling temperature T

in two supercooled liquids, CKN (solid

symbols) and CRN (open symbols), from plots of the temperature (T ) dependences of three different

quantities: top panel, the height of the dielectric-loss minimum; central panel, the position of the

dielectric-loss minimum; and bottom panel, the α-peak position. Representations along the vertical

axes have been chosen so as to produce straight lines according to the predictions of MCT. The

solid lines are consistent with a critical temperature of T

=375 K for CKN, and the dashed lines

with T

=365 K for CRN. Reproduced from Lunkenheimer et al. (1997b).

 American Physical

Society.

exponent parameter value λ =0.78. The value T

=187 K is also in agreement with previous

results from light-scattering studies by Du et al. (1994) and solvation-dynamics experi-

ments (at 176 K) by Ma et al. (1996) on the same material. The neutron-scattering stud-

ies by Börjesson et al. (1990), however, gave a much higher value for T

(180–200 K).

Subsequent reexamination of PC by Wuttke et al. (2000) with neutron-scattering mea-

surements improved this result. Those authors obtained T

≈ 182 K (corresponding

to λ =0.72).

The α-relaxation regime

The relaxation of the correlation function beyond the corresponding plateau f

of the

so-called NEP and subsequent to the von Schweidler decay is generally referred to as α-

relaxation. In the close vicinity of the dynamic-transition point the α-relaxation is

8.2 Evidence from experiments 405

described to leading order in terms of a temperature-independent master function. This

also implies time–temperature superposition. However, as the distance from the transition

increases, correction terms of O(

) to this master function become signiﬁcant (see

eqn. (8.1.58)). Furthermore, the effects of ergodicity-restoring mechanisms of the extended

MCT will also inﬂuence the predictions for ﬁnal relaxation in the theoretical model. A few

characteristic properties of α-relaxation can be listed as follows.

1. The temperature dependence of the α-peak. The time scale of α-relaxation τ

increases as |

−γ

with γ =1/(2a) + 1/(2b). The temperature dependence of the

peak frequency is therefore of the form ω

∼ (T − T

)

. This is shown in the low-

est panel of Fig. 8.6, in which ω

1/γ

for CKN is plotted against temperature. The values

of a =0.28 and γ =2.9 used are kept the same as those obtained in ﬁtting ω

and χ

min

as described above. Similar ﬁts with τ

and τ

extracted from light-scattering data

(Li et al., 1992)forCKNgivea =0.28 and γ =2.9 with the corresponding λ =0.81.

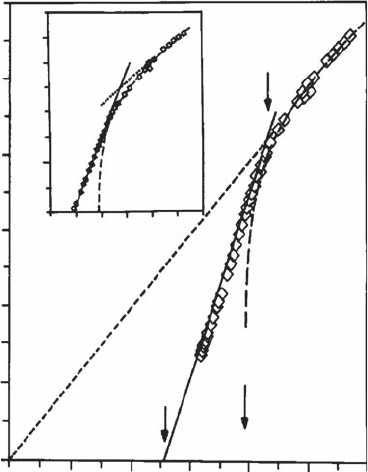
Schönhals et al. (1993) carried out an extensive study of the α-relaxation in PC. The

result for the transition temperature T

=186.6 K is comparable to the correspond-

ing transition temperature T

=180 K from neutron-scattering results (Börjesson et al.,

1990; Elmroth et al., 1992). The temperature dependence of the α-peak frequency ν

(∼ω

) for PC ﬁts to a power law proposed by MCT, ν

∼ (T − T

)

with exponent

γ =2.45, as shown in Fig. 8.7 (Schönhals et al., 1993). The data also ﬁt an Arrhenius

behavior. Beyond a temperature T

, the power-law behavior crosses over to a Vogel–

Fulcher form. The MCT T

(186.6 K) lies in between the temperatures T

and T

, which

are equal to 130 K and 216.6 K, respectively, for PC.

2. The scaling in the α-regime. Time–temperature superposition for the α-relaxation is

a leading-order asymptotic behavior in the simple MCT. Theoretically, even within the

simple MCT, away from the transition temperature-dependent corrections add to the

master function. The role of ergodicity-restoring processes can further affect the sim-

ple result of time–temperature superposition. Experimentally, there have been claims

and counter-claims regarding the validity of this. For depolarized light-scattering spec-

troscopy of o-terphenyl (OTP) (Cummins et al., 1997), the α-peak can be ﬁt with a

Kohlrausch–William–Watts (KWW) form. A temperature-independent stretching expo-

nent β =0.78 was found to ﬁt the data, provided that the higher-frequency wing was

interpreted as an overlap from the β-process or the von Schweidler-type decay. The cor-

responding VS exponent b =0.6 is obtained from the analysis of the β-process (Cum-

mins et al., 1997). Similarly, the temperature-independent β for T > T

was obtained

(a) from light-scattering-spectroscopy data for CKN (Li et al., 1992), glycerol (Wut-

tke et al., 1994), and PC (Du et al., 1994); and (b) from the dielectric-loss data for

CKN (Pimenov et al., 1996), glycerol (Lunkenheimer et al., 1996), and PC (Lunken-

heimer et al., 1997a). Arguments in favor of the temperature independence of β are

based on the reasoning that the observed temperature dependence of β,ifany,isa

result of ignoring the β-process. It has also been argued that the α-relaxation data

conform to a temperature-dependent stretching exponent. From dielectric-susceptibility

406 The ergodic–nonergodic transition

0.30

0.25

0.20

0.15

0.10

150

0.10

0.20

log

∞

)

0.30

200 250

0.05

0.00

100

150

T [K]

MCT behavior

VFT behavior

Arrhenius behavior

1/log

∞

)

T [K]

200

250

300

Fig. 8.7 A plot of 1/ log

(ν

∞

/ν

) vs. temperature T for propylene carbonate (PC) with

log

∞

=13.11. The Vogel–Fulcher–Tamann (VFT) temperature T

,theMCTT

, and the

crossover temperature T

are indicated by arrows. The crossover behavior is demonstrated more

clearly in the inset. Reproduced from Schönhals et al. (1993).

 American Physical Society.

data for low-relative-molecular-mass glass-forming liquid PC over 15 decades, Schön-

hals et al. (1993) obtained a temperature-dependent stretching exponent β – a result that

contradicted the earlier light-scattering results (Elmroth et al., 1992) of a temperature-

independent β.

8.2.2 Glass transition in colloids

Among the various experimental systems studied for testing signatures of the ergodic–

nonergodic transition predicted in the MCT, the nature of the slow dynamics of colloidal

suspensions shows the most prominent agreement. A colloid consists of suspended parti-

cles in a solvent liquid treated as an inert continuous background. Although colloids are

very different from an atomic system, certain characteristic properties are similar. The

effective interactions between the suspended particles in the colloid are made steeply

repulsive in the suspension using suitable techniques and hence its equilibrium phase

behavior mimics that of a hard-sphere system. For example, the melting volume fraction

ϕ =ϕ

=0.542 ± 0.003 in this system is in agreement with that obtained from simulation

8.2 Evidence from experiments 407

for hard-sphere crystals (Hoover and Ree, 1968). The microscopic dynamics in the col-

loid particles involves frequent collisions of solvent molecules, but the positions of these

suspended particles change on a much slower time scale. This vast separation of time

scales allows use of the stochastic Langevin equations for the dynamics of the colloid

particles, in contrast to the deterministic Newtonian equations of motion in an atomic sys-

tem. However, over long time scales the dynamics of the two types of systems are similar,

showing essentially diffusive behavior. The diffusive dynamics becomes extremely slow at

high density, leading to effective freezing in an amorphous conﬁguration. The predictions

of the fully wave-vector-dependent MCT model were compared extensively with the data

from dynamic-light-scattering studies on colloidal systems (van Megen and Underwood,

1993a, 1993b, 1994).

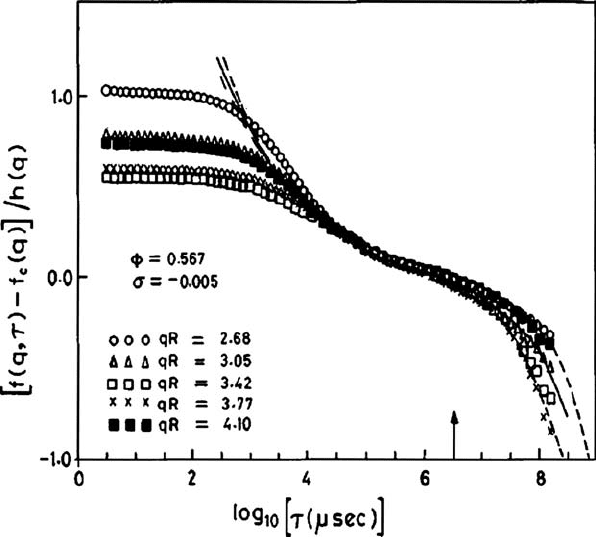
The normalized density correlation function φ(q, t) computed in the light-scattering

experiment on the colloids almost freezes to a constant value for a change of the pack-

ing fraction within 1% around ϕ

=0.574. This structural arrest (within the range

0.574 <ϕ

< 0.581) in colloids has been identiﬁed with the dynamic transition of the

simple MCT. From the relaxation data the β-scaling of MCT is demonstrated in Fig. 8.8.

This plot also tests the q independence of the LHS of (8.1.55) over a suitable range of

time. The theoretical curve shown in Fig. 8.8 consists of the contribution from the β-

process (given by (8.1.49))aswellastheα-relaxation master function . The experimental

data ﬁt to a β-scaling function obtained with the exponent parameter λ =0.758. Using the

hard-sphere structure factor in the formula (8.1.43), the corresponding value of the expo-

nent parameter is obtained as λ =0.77. The agreement between theory and experiments

is thus remarkable in the regime of the β-process. However, it is worth noting that many

parameters are involved in the ﬁtting procedure (see the discussion below). Also, the com-

parisons described above are all based on the simple MCT predicting a dynamic transition.

It has generally been argued that, since the momentum exchange with the colloid particles

occurs on much shorter time scales, the cutoff mechanism is weak in these systems. The

data, even at the highest density, do not rule out the existence of an ergodicity-restoring

process.

8.2.3 Molecular-dynamics simulations

Computer simulation of the dynamics of a small number of particles has been used as an

effective tool for testing the predictions of the MCT. Here the theory can be tested without

any adjustable parameter and using the structural data directly as input. The predictions

of MCT were tested more extensively with MD simulation of a binary soft-sphere sys-

tem by Roux et al. (1989, 1990). These works conﬁrmed the factorization property and

predicted deviations from the Stokes–Einstein relation in the vicinity of the transition.

The extrapolated self-diffusion coefﬁcient vanishes for both components of the mixture

with a power-law exponent roughly equal to 2 (Bernu et al., 1987). Kob and Andersen

(1994, 1995a, 1995b) later investigated a binary Lennard-Jones mixture (BMLJ) exten-

sively against various predictions of MCT. The mixture consisted of 800 type-A and 200

408 The ergodic–nonergodic transition

Fig. 8.8 The density correlation function φ

(t) ≡ f (q,τ) in the scaled form [φ

(t) − f

]/ h

vs.

time t =τ . R is the hard-sphere radius; σ is the separation parameter, and φ is the packing fraction.

The solid line corresponds to the MCT master function σ

1/2

−

(

t )] (see eqns. (8.1.49)–(8.1.52))

corresponding to the exponent parameter λ =0.758; dashed lines are for λ =0.70 and 0.80. The

vertical arrow on the time axis corresponds to the β-relaxation time scale τ

. Reproduced from van

Megen and Underwood (1994).

 American Physical Society.

type-B particles of the same mass m, interacting through the Lennard-Jones potential

(see eqn. (4.3.11) for details). Length is rescaled in units of σ

, temperature in units

of 

, and time in units of

mσ

/(48

)

1/2

. The temperature range studied was

from T =5.0 to a lowest value of T =0.466.

A characteristic transition temperature T

has been identiﬁed for the Kob–Andersen mix-

ture by extrapolating to zero the power-law ﬁt for the self-diffusion coefﬁcient obtained

from simulation. Analysis of the simulation data of a BMLJ gave T

=0.435. On the

other hand, Nauroth and Kob (1997) solved the mode-coupling equations of Bosse and

Thakur (1987) using the corresponding required structure factor directly from the sim-

ulation results and obtained a transition temperature T

=0.922. This was subsequently

improved by application of a different version of the mode-coupling model (Harbola and

Das, 2002) obtained from an approach that takes into account proper momentum conser-

vation in the system. Solution of the equations of the latter model with the same input

8.2 Evidence from experiments 409

structure factors shows that down to T = 0.435 there is no nonzero solution for the

NEPs. This model has so far not been extended to compute the mode-coupling effects

on the self-diffusion coefﬁcient in a binary system. However, the diffusion coefﬁcient D

has been computed using a model for the dynamics of the tagged particle as described in

Section 8.1.3. In this case the memory function for the tagged particle is simply enslaved

to the decay of the density correlation functions C



(see eqn. (8.1.88)). Using results for



obtained from the model of Harbola and Das (2002), D

has been calculated (Harbola

and Das, 2003) and found to extrapolate to zero at T

≈ 0.44.

The MD simulation of the Kob–Andersen mixture has also revealed signatures of the

two-step relaxation process predicted from MCT. A generic feature of the tagged-particle

correlation, signifying cage formation in the dense ﬂuid, is the plateau it reaches over inter-

mediate times prior to ﬁnal relaxation. In the MD simulations the observed plateau ranges

over almost three decades at T =0.466. The height of the plateau has been identiﬁed to be

the value of the NEP and the corresponding time interval treated as the β-process regime

(Kob and Andersen, 1994). Over the time range 3 ≥t ≥1868 corresponding to the so-called

β-relaxation (process) regime and close to the transition point, the simulation data agree

with the factorization property of MCT (see Eq. (8.1.53)). The critical power-law relax-

ation (t

−a

) is not seen in the simulation data. This is rationalized by assuming a strong

inﬂuence of the microscopic dynamics on the early part of the power-law regime. In the

later part of the β-regime, the von Schweidler relaxation with a positive exponent is visible.

Beyond the power-law behaviors, on the scale of α-relaxation the correlation-function data

ﬁt to a stretched-exponential form with stretching exponent β, which is different from the

VS exponent discussed above. At low temperature the relaxation time in the stretched-

exponential form τ

(T ) follows a power-law increase, appearing to diverge (Kob and

Andersen, 1995b) at the same temperature T

as that at which the diffusion coefﬁcient

extrapolates to zero. The exponent of the divergence, γ =2.7, approximately follows the

MCT prediction. However, the exponents of divergence of τ and D

−1

are not the same.

For the self-diffusion coefﬁcients, both the temperature T

and the exponent γ



(say) are

found to be the same for both types of species in the mixture. However, the exponent γ



does not match the corresponding exponent γ found from ﬁtting the diverging behavior of

the α -relaxation time scale around T

. A similar behavior was reported by Schröder et al.

(2000). This presumably indicates that the mechanism of the slowing down for the density

ﬂuctuations is not the same as that for the self-diffusion.

8.2.4 Discussion

In general, the above-cited items of evidence from experiments or simulations in support

of the MCT involve a large number of ﬁtting parameters. In most cases, especially for sys-

tems like CKN and OTP, the crucial inputs of the mode-coupling model are treated as free

ﬁtting parameters. The typical adjustable quantities used are the time scale of transients t

the NEP f , the amplitude h, the transition point T

, the prefactor of the α-relaxation time

scale C, and the exponent parameter λ – there are up to as many as six such adjustable

410 The ergodic–nonergodic transition

parameters. In addition, most of the tested relaxation behaviors are predictions from the

theory at leading order, in the close vicinity of the transition. Often this requires care-

ful adjustment of the time range or temperature range in order to be able to observe the

predicted effect. Thus, for example, the predicted factorization property is valid only close

to the transition and over the time window of power-law relaxation. It is not valid in the

longer-time part of the α-relaxation. Similarly, the predicted temperature independence of

the stretching exponent β (and hence time–temperature superposition) is expected to hold

only when the liquid is neither too close to T

(so that the ergodicity-restoring mechanisms

do not intervene) nor too far from the transition (in which case the leading-order behavior

would not hold). Additional correction terms to the leading-order results of the β-scaling,

as well as the α-scaling, become important (Hinze et al., 2000) as the distance from the

transition increases.

It is important to note that in the above analysis of experimental data the existence

of a dynamic transition point is inferred only indirectly. The critical exponents related

to the divergences in the MCT are completely system-dependent and cannot be classi-

ﬁed into universality classes. In fact, the experiment really never showed a direct sig-

nature of T

. Assuming that there is a substantial blurring or rounding of the transition,

which masks it, ﬁtting the experimental data with scaling assumptions is usually pos-

sible, within some error around the rounded “singularity.” This ﬁtting procedure which

seeks consistency between the two steps of relaxation also identiﬁes, indirectly, the loca-

tion of the dynamic-transition point. On the other hand, using the static structure fac-

tor of the liquid as an input, the corresponding MCT equations can be solved to obtain

the location of the dynamic-transition point. This is a ﬁrst-principles calculation without

any adjustable parameter. However, the transition density thus obtained from the MCT

for a simple hard-sphere system does not seem to agree well with the corresponding

control-parameter value at which a possible structural arrest is interpreted in the simu-

lations or experiments. This is presumably linked with the low-order perturbative nature

of MCT, in which the one-loop model is used to obtain the renormalized transport

coefﬁcient.

It should be noted here that the two-step relaxation of MCT is different from Goldstein’s

picture of two time scales, which was discussed in Section 4.3. The former occurs above

, where barrier hopping is not dominating the dynamics, and is related to the initial

stages of supercooling. The vibrational and conﬁgurational parts of the dynamics depicted

in Goldstein’s picture of an energy-landscape description, on the other hand, occur when

barrier hopping is strongly inﬂuencing the dynamics. The MCT, at least in its present form,

is not suitable for understanding the behavior of the deeply supercooled liquid in which the

viscosity rises by 14 orders of magnitude (equivalent to time scales of the order of 10

or so). More recently, phenomenological extensions of MCT have been proposed in order

to extend the theory further in this direction (Bhattacharyya et al., 2005). Another related

and important issue here is the intervention of the crystallization process, which becomes

more likely with increasing supercooling. In the MCT approach depicted above, the liquid

dynamics is considered to be in a stationary state not too far below its freezing point and it is