Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

8.1 Mode-coupling theory 381

the nonlinear coupling of δρ

and δρ in the equation of motion for the tagged-particle

momentum, we obtain

∂g

∂t

+ 

+ v

∇

+ V

[q − k, k]ρ

(k)δρ(|q − k|) = ζ

. (8.1.84)

The vertex function V

in the third term on the LHS is given by

(q − k, k) =

βm

c(k). (8.1.85)

The RHS of the expression (8.1.81) for the tagged-particle correlation is obtained as

(q, z) =



z −

z + i 

(q, z)



−1

. (8.1.86)

The kernel 

in (8.1.81) is now renormalized due to the nonlinear coupling of the tagged-

particle density ρ

with ρ in the equation of motion (8.1.84) for the tagged-particle density,



(q, z) = 



izt



(q, t)dt. (8.1.87)

At one-loop order the mode-coupling contribution is obtained as



(q, t) =

βm



(2π)

[(

q · k)c(k)]

S(k)F

(q − k, t)φ(k, t ) ≡˜m

(q, t), (8.1.88)

where

q denotes the unit vector. The correlation of the tagged-particle momentum also

follows in a straightforward manner from the above analysis. The renormalized expression

for the longitudinal tagged-particle current–current correlation is obtained as

(q, z) =

z + i 

(q, z)

. (8.1.89)

The transverse current correlation has a similar form. It is useful to note here that the

renormalized model given by (8.1.86)–(8.1.88) for the tagged-particle correlation is also

obtained in the so-called microscopic approach of the projection-operator formalism by

following a procedure similar to that described in Appendix A7.4 (Götze, 1991). This

involves taking projections on the space of coupled slow modes C

(kp ...)=

δρ (k)δρ

(p)... The same model for tagged-particle correlation was studied in order to

argue that the self-diffusion coefﬁcient goes to zero (Bengtzelius et al., 1984) at the dynamic

transition point of MCT.

Let us consider the implication of having a mode-coupling kernel of the form (8.1.88)

described above. The time evolution of the tagged-particle correlation function is now com-

pletely enslaved to that of the density correlation function. The self-correlation F

(q) in

(8.1.81), driven by the memory function (8.1.88), freezes to f

at the dynamic transition

382 The ergodic–nonergodic transition

point of the MCT described by (8.1.31)–(8.1.33). The corresponding equation for the non-

ergodicity parameter f

(the long-time limit of the tagged-particle correlation F

(q, t))is

1 − f



˜m

(q, t →∞) ≡ H

[ f

], (8.1.90)

with 

. This is similar to the corresponding equation (8.1.36) for the total den-

sity correlation function. In the close vicinity of the dynamic transition, on the liquid side

(q, t) follows a sequence of relaxation similar to that of the density correlation function

as discussed earlier in Section 8.1.1. Away from the transition, a correction similar to what

was already discussed for the density correlation function applies (Fuchs et al., 1998)in

this model for the tagged-particle motion.

The hydrodynamic behavior of the tagged-particle motion is obtained from the q → 0,

z → 0 limit of the correlation function F

(q, z) given by eqn. (8.1.86). There is diffusive

behavior, as follows from the result

(q, z) =

z + iq

(0, 0)

, (8.1.91)

where the renormalized diffusion coefﬁcient is obtained as

(0, 0) =

βm

(0, 0)

. (8.1.92)

At the dynamic transition point, the mode-coupling contribution given by eqn. (8.1.88)

develops a 1/z pole in 

. This is a consequence of the freezing of the density correla-

tion function at the transition. Hence the self-diffusion coefﬁcient D

→ 0 in the long-

time limit. The corresponding mean-square displacement

(t)

freezes in time, signifying

complete localization of the particle.

The above model for the tagged-particle correlation has been very widely used in the

literature for studying slow single-particle dynamics in a dense liquid. In this theory the

tagged-particle correlation completely freezes and the self-diffusion coefﬁcient goes to

zero at the mode-coupling or the ENE transition point. This is a consequence of the simi-

larity of the renormalized model for the self-correlation function given by (8.1.86)–(8.1.88)

to its counterpart for the total density correlation. In its present form the memory kernel for

the tagged-particle dynamics is completely enslaved to the collective density correlations

and causes the self-diffusion coefﬁcient to vanish at the MCT transition point.

This coupling of the autocorrelation of the total density ﬂuctuations and that of the

tagged-particle density in the memory function is rooted in construction of the model for

single-particle dynamics as described above. The two-step continued-fraction form for the

self-correlation follows from the equations for the tagged-particle density ρ

and its current

. These equations are similar to the corresponding equations for the total mass density ρ

and momentum density g, both of which are microscopically conserved quantities. In the

case of single-particle dynamics, only the tagged-particle density ρ

(and not its current g

)

is a microscopically conserved property.

8.1 Mode-coupling theory 383

The microscopic variables ˆρ

and ˆg

are connected by the simple continuity equation

(8.1.62), but it is not possible to justify the relation (8.1.70) connecting the coarse-grained

quantities ρ

and g

. Since g

is not a slow variable, the dynamic equation for ρ

should

in fact involve dissipation and noise. There is also no basis for assuming a separation of

time scales between the “noise” and “regular” parts in the equation for g

. The theory of

the single-particle dynamics should in fact follow in a natural way from the one-particle

limit of the binary mixture. Of related interest is the Smoluchowski level description for

single-particle dynamics in a colloid, which is formulated (Schweizer and Saltzman, 2003,

2004) by treating the displacement r(t) of the particle as a slow variable.

8.1.4 Dynamical heterogeneities and MCT

The MCT takes into account the effects of correlated dynamics of the particles in a high-

density liquid. The different aspects of dynamical heterogeneities seen in the computer

simulations should follow in a natural way from these mode-coupling models. Thus, for

example, the non-Gaussian parameter α

(t) (see eqn. (1.3.61) for its deﬁnition) is obtained

by evaluating the tagged-particle correlation function F

(q, t) for very small q truncated

at O(q

) (Kaur and Das, 2002; Fuchs et al., 1998). From the expansion given in eqn.

(1.3.58), it follows that for small q the curve (1/q

)(1 − F

(q, t)) vs. q

is a straight line

with intercept r

(t)/6 and slope −r

(t)/120. The term α

(t) can then be evaluated

using these two quantities from eqn. (1.3.61). In a simple hard-sphere system, for example,

the bare contribution to 

(q, t) is given by 

=2/(3t

), t

being the Enskog collision

time deﬁned in eqn. (5.3.101). The direct correlation function c(k) and the static structure

factor S(k) are obtained as the Percus–Yevick solution with Verlet–Weiss correction. To

evaluate the F

(q, t) in the small-q range, the memory function



(q, t) is expressed as

an expansion in q given by



(q, t) =



(0)

(t) + q



(2)

(t) + q



(4)

(t) +···. (8.1.93)

The successive



(n)

are obtained by using the Taylor-series expansions of F

(|q −



k|, t)

and V

(q − k, k) in eqn. (8.1.88).Theα

(t) obtained from the mode-coupling equation

develops a peak over a time scale longer than the microscopic times and is similar to

the one observed in the computer-simulation studies of Kob et al. (1997) discussed in

Section 4.4.1. In the simple MCT model with the ideal dynamic transition at η

, the time

at which this peak of α

(t) occurs keeps growing on approaching η

. Above η

this peak

never occurs; instead, α

(t) attains a constant value for long times for the packing fraction

of 0.540 for the hard-sphere system. In reality, however (as we will see later in this chapter),

the dynamic transition at η

is ﬁnally removed due to ergodicity-restoring mechanisms

operating in the compressible liquid. The peak in α

(t) therefore survives at high density

in an extended version of the MCT. The behavior of α

(t) with increasing density is shown

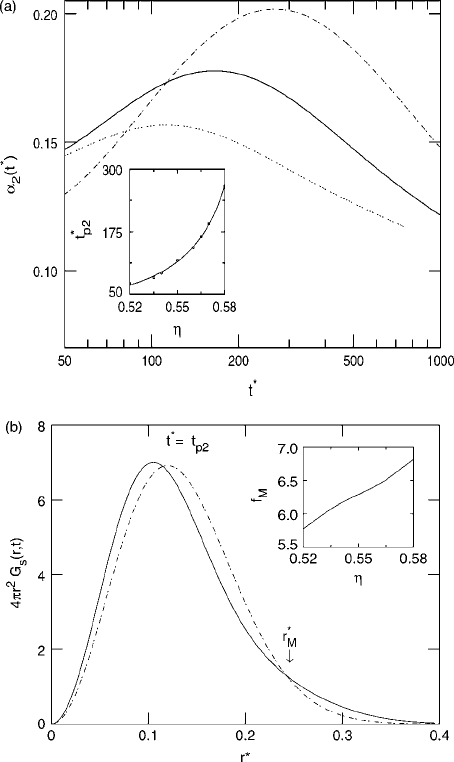
in Fig. 8.2(a).

The result for the tagged-particle correlation G

(r, t) vs. r obtained from the MCT is

used to set a criterion for identifying a set of particles that are more mobile than the rest

384 The ergodic–nonergodic transition

Fig. 8.2 (a) The non-Gaussian parameter α

vs. t

∗

for the hard-sphere system at packing frac-

tions η =0.550 (dotted), η =0.565 (solid), and η =0.580 (dot–dashed) as obtained from solution

of extended MCT equations. In the inset, the variation of t

vs. η is shown for this model. (b) The

fraction of mobile particles obtained using the MCT: G

(r, t

) vs. r

∗

=r/σ for the hard-sphere

system at packing fraction η =0.565. The dashed curve is the corresponding Gaussian distribution

function G

(r, t

) (see the text). The inset shows the variation of the fraction of mobile particles f

vs. η. Reproduced from Kaur and Das (2002). Both parts

 American Physical Society.

of the particles. This was already described in Section 4.4.1 with eqns. (4.4.3) and (4.4.4)

for the BMLJ systems (Kob et al., 1997). The Gaussian function G

(r, t) is deﬁned in

terms of r

(t) and compared with the full G

(r, t). The distance r

is identiﬁed from

the largest value of r at which the two curves G

and G

intersect (see Fig. 8.2(b)). The

time t

at which the tagged-particle correlation is considered is chosen (similarly to what

8.1 Mode-coupling theory 385

is done in simulations) to be the one at which the corresponding non-Gaussian parameter

(t) shows a large peak. The fraction f

of particles that have traveled a distance larger

than r

is obtained from the area under the G

(r, t

) vs. r curve beyond this distance r

and is displayed in the inset.

The mode-coupling model has also been extended (Biroli and Bouchaud, 2004) to study

the four-point correlation function which is associated with the dynamic correlation length

discussed in Section 4.4.2. The density being the dominant variable, one can focus on

the four-point correlation function deﬁned in terms of the collective density

(r, t;r

, t

) =



ρ(0, 0)ρ(r

, t

)ρ(r, t)ρ(r + r

, t + t

)



−



ρ(0, 0)ρ(r

, t

)



ρ(r, t)ρ(r + r

, t + t

)



. (8.1.94)

(r, t;r

, t

) is a measure of the cooperativity of the dynamics. The corresponding

Fourier–Laplace transform χ

of the four-point function in the small-wave-vector limit

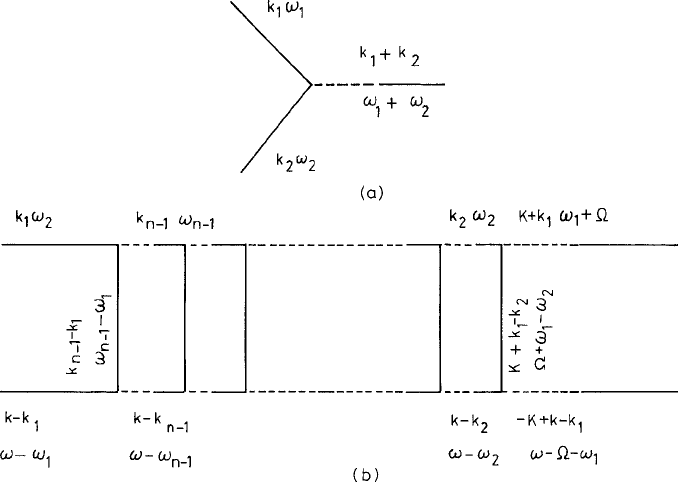
is obtained using diagrammatic methods. The four-point function has been dealt with by

making simpliﬁcations such as that there is only one type of cubic vertex involving the

density ρ and its conjugate MSR ﬁeld ˆρ. The four-point correlation function is expressed

as a sum of ladder diagrams (shown in Fig. 8.3). The diagrammatic expansion to all orders

then takes the form of an inﬁnite geometric series,

≡ 1 +

M[ψ(t)]+

[ψ(t)]+···

1 −

M[ψ(t)]

, (8.1.95)

where

M[ψ(t)]is the corresponding one-loop contribution in the ladder diagrams in terms

of the correlation function C. This also requires assuming the validity of the ﬂuctuation–

dissipation theorem for the relation between the correlation and response functions. The

ideal transition point corresponds to the solution of the one-loop equation for the non-

ergodicity parameter {f

} at the transition point T

M[ψ(t)]=1. For T < T

the

density correlation ψ(t) = f + ψ

(t) (see eqn. (8.1.9)). By expanding the denominator of

the RHS of eqn. (8.1.95) around f = f

and using the result that in the nonergodic phase

f − f

∼

√

 (see eqn. (8.1.24)), we obtain that the four-point correlation χ

for T < T

diverges like 1/

√

. The wave-vector-dependent propagator behaves like (



√

)

−1

For T > T

, on the other hand, a simple Taylor-function expansion around the criti-

cal f

shows that the propagator behaves like (k

+ )

−1

. Using the analogy with the

typical Ornstein–Zernike form for the two-point functions, the above result for the prop-

agators indicates that the corresponding dynamic correlation length ξ

diverges like 

−ν

with ν =

and ν =

for T < T

and T > T

, respectively. Later, three-point correlation

functions similar to eqn. (4.4.18) have been considered in the so-called inhomogeneous

mode-coupling theory (Biroli et al., 2006), and it was predicted that the exponent ν =

;

above is in fact ν =

, predicting a slower growth of ξ

on approaching the transition

from above. In a related work Szamel (2008) did an analysis of the four-point correla-

tion function for interacting Brownian particles, claiming that the former can be expressed

in terms of three-point functions closely related to the three-point susceptibility introduced

386 The ergodic–nonergodic transition

Fig. 8.3 (a) The crucial cubic vertex in the MSR action functional constructed with the DDFT equa-

tion for density. (b) The typical ladder diagram for the four-point correlation function constructed

with the cubic vertex of (a). From Biroli and Bouchaud (2004). Both parts

 Europhysics Letters.

by Biroli et al. (2006) and the standard two-point correlation function. Since the order

parameter in MCT is a two-point function relating ﬂuctuations at two different times, the

corresponding susceptibility is a four-point function. The divergence of the latter is used

as an indicator of diverging correlation length. However, as outlined above, obtaining this

result involves using rather simple arguments and approximate treatment of the diagram-

matic expansion for the four-point correlation function with a class of ladder diagrams only.

Finally, since the transition at T

is cut off, the divergence predicted here does not imply a

sharp increase of ξ

, in agreement with ﬁndings in simulations. The normalized four-point

correlation function χ(t) =|δρ (k

m,t

)δρ(−k

m,0

/|δρ (k

)δρ(−k

|

evaluated at the

peak of the structure factor (k

) displays a peak that grows with density. This quantity has

recently been computed from a direct solution of the nonlinear Langevin equations (see

Section 8.3.3) for a one-component Lennard-Jones system. The result for this four-point

function showing a growing peak is shown in Fig. 8.4.

Other cases of growing correlation length have also appeared in mode-coupling models.

The ﬁrst of such cases refers to the random diffusion model (RDM) (Mazenko, 2008;

2006), which is somewhat similar to the so-called DDFT model with a single density

variable. Here, unlike in the above example of higher-order correlations, the growing

correlation length has been identiﬁed from the dynamic structure factor. We discuss this

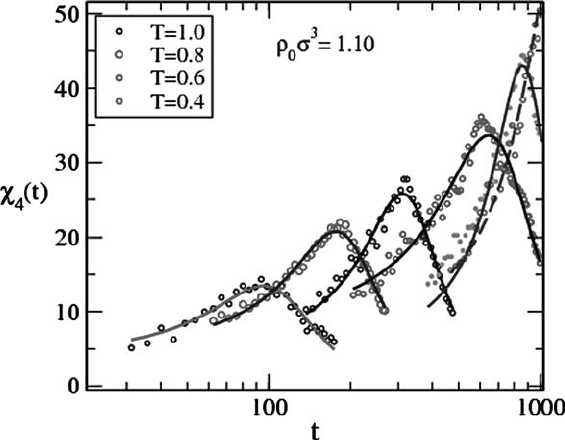
8.1 Mode-coupling theory 387

Fig. 8.4 Results from numerical solution of the equations of nonlinear ﬂuctuating hydrodynamics.

The four-point function χ

, t) at the peak of the structure factor q

(see eqn. (8.3.17) for its

deﬁnition) is shown vs. time t in reduced Lennard-Jones units. The reduced density is ﬁxed at 1.10

and the corresponding reduced temperatures are shown in the ﬁgure. The lines are best ﬁts of the

points to a Lorentzian form (Sen Gupta and Das, 2010, unpublished work).

below at the end of Section 8.1.6. Another example of a growing length scale refers to the

viscoelastic behavior of the supercooled liquid. The MCT, which provides a microscopic

explanation for visco-elasticity, has been used (Alhuwalia and Das, 1998; Das 1999) to

identify a growing length scale l

. The latter is associated with the maximum wavelength

of the shear waves. Identiﬁcation of this length scale from computer simulations of an

equimolar mixture of soft-sphere liquids was discussed in Section 4.3.1. The crossover in

the behavior of the diffusive shear mode to propagating shear waves is obtained from the

solution of the self-consistent set of MCT equations given by (7.3.69)–(7.3.72). The relax-

ation of the shear mode is obtained here using the static structure factor of the liquid as the

sole input. The solution of the MCT equations identiﬁes the minimum wave number q

min

above which the shear mode is propagating. This crossover in the behavior of the shear

modes is intimately connected to the shear viscosity of the supercooled liquid. If the shear

viscosity diverges, implying that the corresponding Laplace transform develops a pole,

η(z) ∼ 1/z, then from eqn. (7.3.69) it follows that the shear modes are propagating for

all wave numbers, i.e., q

min

=0. Hence, as the shear viscosity diverges at the ideal transi-

tion point, the corresponding l

also diverges. Therefore, in the ideal nonergodic phase, for

all temperatures below the dynamic transition point l

→∞. This is unlike a correlation

length, which shows divergence only at the transition point. In reality, however, since the

388 The ergodic–nonergodic transition

ideal transition is cut off, the divergence of l

is avoided, but l

grows with increasing shear

viscosity. Recently evidence of such length scale was reported (Torchinsky et al., 2011)

from study of shear acoustic phonons in supercooled triphenylphosphite (TPP).

8.1.5 Linking DFT with MCT

In this section we demonstrate that some of the results from the mode-coupling models

for the dynamics of the frozen supercooled liquid are linked to a static density-functional

description of the amorphous solid state. This link is established here, focusing on the

tagged-particle dynamics as predicted from the two different descriptions of the frozen

solid. For the mode-coupling model we have seen that, within the approximations made

in the naive mode-coupling theory, the self-diffusion coefﬁcient D

of a tagged particle is

zero below the dynamic transition point. In the thermodynamic picture, on the other hand,

the glassy state is characterized as one in which the individual particles are oscillating

around a set of lattice sites {R

} situated on a random lattice. In the case of harmonic

motion of these particles, the system is termed a harmonic solid. The present discussion,

which is based on Kirkpatrick and Wolynes (1987), bridges the two basic theories we are

dealing with in this book, i.e., the density-functional theory (DFT) and the mode-coupling

theory (MCT).

The key quantity for analyzing the single-particle dynamics is the tagged-particle den-

sity correlation function given by (8.1.86). The Laplace transform of the related quantity

tagged-particle current correlation is obtained in the form (8.1.89). The mode-coupling

effects are included here in terms of the self-energy



(0, t) given by eqn. (8.1.88).In

the naive mode-coupling model, the transition of the supercooled liquid to the nonergodic

glassy state occurs at a critical density. This is driven by a key feedback mechanism as

a result of which the density correlation function freezes in the long-time limit. As was

pointed out above, due to the form (8.1.88) of the mode-coupling contribution the freez-

ing of the density correlation function implies that the Laplace transform of the memory

function



(0, t) develops a 1/z pole. In the small-z limit we write



(z) =



∞

+ RT, (8.1.96)

where



∞

is the long-time limit of



(0, t),



∞



(t →∞), (8.1.97)

and RT represents the regular terms. The self-diffusion coefﬁcient of the tagged particle

goes to zero, implying complete localization. The development of the 1/z pole or nonzero

value for 

∞

is therefore crucial for the localized motion of the single particle. Assuming

the latter to be harmonic in nature, a simple relation is reached between the corresponding

spring constant and



∞

. Using the form (8.1.96) for the Laplace transform of the self-

energy



(t), it easily follows from the denominator of the RHS of eqn. (8.1.89) that

the current correlations represent damped harmonic waves signifying vibration around the

8.1 Mode-coupling theory 389

lattice sites. The corresponding frequency of oscillation ω

and hence the spring constant

of the vibration can be obtained from the pole as

mκ

= ω



∞

. (8.1.98)

The above relation follows from a purely dynamic route (MCT) for the localized single-

particle dynamics.

In the DFT described earlier in Chapters 2 and 3 the equilibrium free energy of the solid

state is obtained by a minimization of the suitable functional with respect to the inhomo-

geneous density function. The solid-state density is characterized by particles oscillating

around their mean positions forming a lattice. In the case of a crystal this lattice has long-

range order, whereas for an amorphous solid this is a random structure representing a

metastable state. The test density function which has been most effectively used in the

DFT approximates the density proﬁles in terms of normalized Gaussian functions centered

around a set of lattice points {R

n(x) =

(

)

3/2



−α(x−R

)

≡



i=1

(|x − R

|), (8.1.99)

where φ

(r) = (α/π)

3/2

exp(−αr

). In the harmonic solid the spring constant of oscilla-

tion of a single particle around the lattice site is simply related to the width parameter α

for the Gaussian proﬁles. To see this, we ﬁrst note that for the harmonic solid the average

kinetic and potential energies are the same, each being equal to k

T /2, i.e.,

p



x

=

. (8.1.100)

The average mean-square displacement for the single particle in this case is given by

x

=1/(2α). On combining this with eqn. (8.1.100) we obtain the relation

= 2(k

T )α (8.1.101)

linking the spring constant with the width parameter. Now, using the relation (8.1.98),the

width parameter α is related to the self-energy



∞

α =

βm



∞

. (8.1.102)

The above relation then serves as the key link between the DFT description of the harmonic

solid and the mode-coupling kernel. In the ergodic state



∞

→0 and hence α vanishes,

corresponding to the liquid state in the DFT description. The long-time limit



∞

for the

memory kernel



(t) follows from the result (8.1.88):



(0, t) =

3βm



(2π)

(k)S(k)F

(−k, t)φ(k, t). (8.1.103)

Equation (8.1.102) for α is now obtained in the form

α =



(2π)

(k)S(k)F

(−k, t →∞)φ(k, t→∞). (8.1.104)

390 The ergodic–nonergodic transition

A self-consistent equation for the width parameter α is thus obtained by applying the

Vineyard approximation φ(k, t) = F

(k, t). For the localized Gaussian density proﬁles the

long-time limit of the tagged-particle density correlation is expressed in terms of the width

parameter as

(k, t →∞) = exp



−

4α



. (8.1.105)

Using this approximation, the RHS of the expression (8.1.104) for the width parameter α

reduces to the form

α =



(2π)

c(k)h(k)exp



−

2α



(8.1.106)

We deﬁne h(k) =c(k)S(k). The above result is an expression for the width parameter of

the localized Gaussian density proﬁles obtained from dynamic considerations using the

simple mode-coupling model for tagged-particle dynamics.

In the DFT approach, for the harmonic solid we can estimate the spring constant κ

also using equilibrium considerations. Here we start from the corresponding expression

for the free-energy functional treated as a function of the inhomogeneous density of the

harmonic solid. In Appendix A8.1 we compute the variation of the free energy of the solid

corresponding to a displacement δR

for a single particle tagged as 1. The free energy as a

quadratic functional of the displacement δR

is obtained as

βF





c(|x − x







i=2

(|x



− R

|)∇

∇

(|x − R



· δR

δR

+···

≡

δ R

1 j

. (8.1.107)

In the last equality we treat the quadratic expression for the free energy to obtain κ

as the

tensor of spring constants for the harmonic motion of the tagged particle 1 around R

.For

an isotropic system we denote this as κ

, which is a scalar. We obtain from (8.1.107),

with some simple algebra, the following result for α:

α =



2π

c(k)h

(k)exp



−

2α



(8.1.108)

where c(k) is the Fourier transform for the direct correlation function c(x) for the isotropic

liquid. The function h

(k) on the RHS of (8.1.108) is obtained as

(k) =



i=j=1

ik ·(R

−R

)

, (8.1.109)