Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

A7.2 The MSR ﬁeld theory 351

the Jacobian is therefore essential in maintaining causality. The latter also ensures that the

response functions are time-ordered. In our discussion of the models described in this book,

we treat the Jacobian as a constant. In some cases (see the discussion with a p-spin model

in Section 8.4, eqn. (8.4.10)) the Jacobian can also be simply absorbed as a correction

term in the action functional (De Dominics, 1978; De Dominicis and Pelti, 1978)inthe

thermodynamic limit.

A7.2 The MSR ﬁeld theory

Here we establish the crucial relations (7.1.28)–(7.1.31) which express self-consistently

the self-energy  of the MSR ﬁeld theory in terms of the full correlation functions G.

We start from the standard functional identity,



D(%)

δ%(1)

−A

i(%)

]=0, (A7.2.1)

corresponding to the action functional (7.1.22) having cubic vertices. The above identity is

equivalent to

δ A

δ%(1)

= 0. (A7.2.2)

Using the expression (7.1.22) for the MSR functional, we obtain

−1

2)G(

2) + V (1

3)%(

2)%(

3)=ξ(1). (A7.2.3)

We have adopted in the above equation the summation convention, i.e., the repeated indices

(with a bar) are summed over. We also use the fact that the three-point vertex function

V (123) is symmetric under exchange of the indices. This is an important property of the

vertex function V and we use it repeatedly in this chapter:

δξ(2)

G(1) =

δξ(2)



−A

%(1)

=%(1)%(2)−%(1)%(2)

=δ%(1)δ%(2)≡G(12). (A7.2.4)

The above equation reduces to the standard result

%(1)%(2)=%(1)%(2)+G(12). (A7.2.5)

On reorganizing the terms in (A7.2.3), we obtain

−1

2)G(

2) + V (1

2)G(

3) + G(

= ξ(1). (A7.2.6)

352 Appendix to Chapter 7

On taking one more derivative of eqn. (A7.2.6) w.r.t. the current ξ(2), we obtain the

equation

−1

2)G(

22) + V (1



22)G(

3) + G(

2)G(

32) +

δξ(

32)



= δ(12).

(A7.2.7)

Starting from the deﬁnition of the inverse of a matrix,

−1

2)G(

21) = δ(12), (A7.2.8)

and differentiating with respect to ξ(3), we obtain

δG

−1

δξ(3)

22) + G

−1

δG(

22)

δξ(3)

= 0, (A7.2.9)

or, equivalently,

δG(23)

δξ(4)

=−G(2

δG

−1

(

δξ(4)

43). (A7.2.10)

By substituting (A7.2.9) into (A7.2.7) we obtain

−1

2)G(

22) + 2V (1

2)G(

3)G(

22)

− V (1

3)G(



δG

−1

(

δξ(



52) = δ(12). (A7.2.11)

On formally deﬁning the self-energy matrix  in terms of the inverse of the full Green

function, we obtain



−1

2) −

(1

22) = δ(12), (A7.2.12)

where the inverse of the full Green-function matrix in the form of the Schwinger–Dyson

equation is given by:

−1

= G

−1

2) − (1

2). (A7.2.13)

The self-energy matrix  is obtained as

(12) =−2V (12

3)G(

3) + V (1

3)G(



δG

−1

(

42)

δξ(



, (A7.2.14)

with the renormalized three-point vertex function R(123) deﬁned as

−

δ(12)

δξ(3)

≡

δG

−1

(12)

δξ(3)

= R(12

3)G(

33). (A7.2.15)

The following self-consistent expression is obtained for the self-energy  matrix in terms

of correlation functions:

(12) =−2V (12

3)G(

3) + V (1

3)G(

4)R(

5)G(

3). (A7.2.16)

A7.2 The MSR ﬁeld theory 353

Next we obtain a self-consistent equation for computing the vertex function R as a pertur-

bation series in the bare vertex V .Fromeqn. (A7.2.6) we see that ξ(1) can be expressed

in terms of G(1) and G(12), order by order in perturbation theory. We therefore make a

change of variables from ξ(1) to {G(1), G(12)} and use the chain rule to write

δG

−1

(12)

δξ(3)

δG

−1

(12)

δG(

δξ(3)

δG

−1

(12)

δG(

δξ(3)

. (A7.2.17)

Now, on substituting the useful identity (A7.2.10), the above relation reduces to

δG

−1

(12)

δξ(3)

δG

−1

(12)

δG(

43) −

δ(12)

δG(

δG

−1

(

δξ(3)

4). (A7.2.18)

We use the Schwinger–Dyson equation (A7.2.13) to replace the functional derivatives

δG

−1

(12)

δξ(3)

−→ −

δ(12)

δξ(3)

(A7.2.19)

and obtain eqn. (A7.2.18) in the form

δ(12)

δξ(3)

δ(12)

δG(

33) +

δ(12)

δG(

δ(

δξ(3)

4). (A7.2.20)

The above relation is written as the following self-consistent equation for the three-point

vertex function R(123):

R(123) = (123) +U (12

4)G(

5)G(

6)R(

53), (A7.2.21)

with the three- and four-point vertex functions (123) and U (1234) deﬁned as

(123) ≡

δ(12)

δG(3)

, (A7.2.22)

U (1234) ≡

δ(12)

δG(34)

. (A7.2.23)

Equation (A7.2.21) for the renormalized vertex function can easily be rearranged with the

following formal rearrangements (to avoid clutter we drop the arguments of the various

functions, with the understanding that all the indices and coordinates except the external

three points (123) are summed over):

R =  + UGGR

=  +UGG +UGGUGGR

=  +UGG +UGGUGG +UGGUGGUGGR

=  +

[

U + UGGU + UGGUGGU +···

]

GG

=  + T GG, (A7.2.24)

where the new four-point vertex T is now obtained in terms of the integral equation

T = U + UGGU + UGGUGGU +···≡U + UGGT . (A7.2.25)

354 Appendix to Chapter 7

Hence we obtain the following self-consistent integral equations for the vertex functions:

R(123) = (123) + T (1

53)G(

6)G(

7)(

62). (A7.2.26)

The four-point kernel T (1234) is to be determined from the integral equation

T (1234) = U (1234) +U (1

34)G(

4)G(

5)T (

423). (A7.2.27)

The three-point vertex function (123) is obtained by solution of the following self-

consistent equation:

(123) =

δG

−1

(12)

δG(3)

=−

δ(12)

δG(3)

−

δ(12)

δG(

δG(3)

= 2V (123) +



δ(12)

δG(



6)G(

δG

−1

(

δG(3)

. (A7.2.28)

In obtaining the last equality we express the derivative in the second term on the RHS as

δG(12)

δG(3)

=−G(1

δG

−1

(

δG(3)

32). (A7.2.29)

The above result follows from the identity (A7.2.10). Equation (A7.2.28) is now obtained

in the form of a self-consistent equation for the three-point vertex function (123),

(123) = 2V (123) +U (12

5)G(

6)G(

7)(

7). (A7.2.30)

Equations (A7.2.16), (A7.2.26), (A7.2.27), and (A7.2.30) provide a formal structure of the

renormalization of the linear theory in terms of the self-energy matrix  expressed in terms

of correlation functions. The lowest-order contribution (in the perturbation theory in terms

of the bare vertex function V )to(12) is obtained by replacing both R and  with the

bare vertex 2V ,

(12) = 2V (1

3)G(

4)V (

5)G(

3), (A7.2.31)

where we assume that the symmetric state corresponds to current ξ = 0 and that the one-

point function G(1) = 0, and hence the ﬁrst term in (A7.2.16), disappears. Using this form

for  in the deﬁnition (A7.2.22), the lowest-order contribution to the four-point vertex

function is obtained as

U (1234) = 4V (12

3)G(

4)V (34

4). (A7.2.32)

The above result for U, when substituted into the renormalization for the vertex func-

tion  (and hence R), gives the two-loop contribution to the self-energy. The bare vertex

function V (123) is determined from the nonlinearities in the equations of motion for the

slow modes. The standard set of graphs representing the coupled equations (A7.2.16) and

(A7.2.26) is shown in Fig. A7.1. A graphical expansion for  in terms of the bare vertices

V and the full correlation functions G can be obtained to any arbitrary order in principle.

In Fig. A7.2 the diagrammatic expansion up to second order in k

T is shown. In practice

the renormalization has been considered only up to one-loop order.

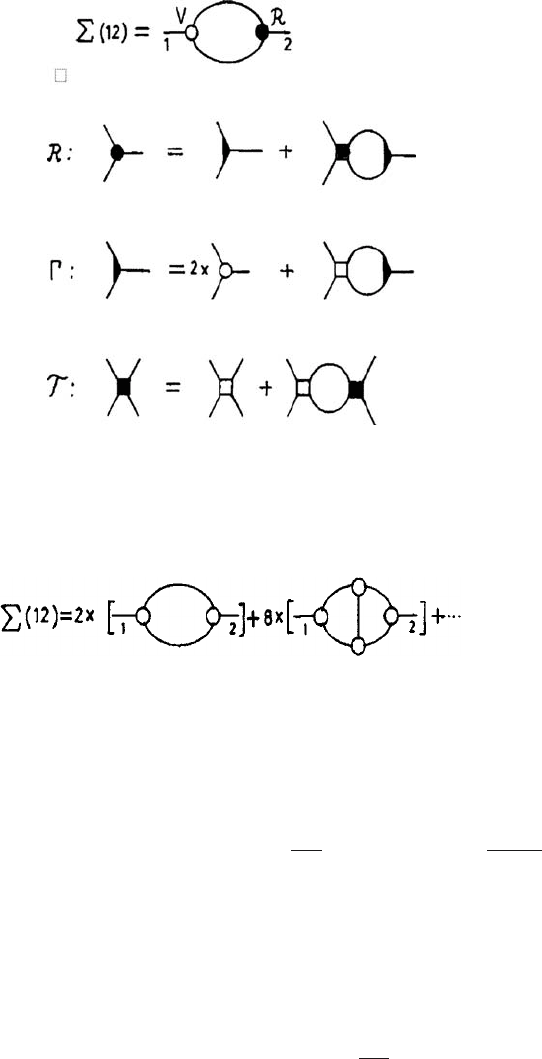
A7.3 Invariance of the MSR action 355

Fig. A7.1 The diagrammatic expansion for the self-energy  as given by the self-consistent expres-

sions in eqns. (A7.2.16)–(A7.2.27). Open and closed  each with three attached legs represent

V (123) and R(123), respectively. Closed  with three attached legs represent (123). Open and

closed squares with four attached legs represent U (1234) and T (1234), respectively. The lines

joining both ends with the vertices represent fully renormalized correlation or response functions.

Fig. A7.2 The expansion for the self-energy  as given in Fig. A7.1 up to second order in k

T .

A7.3 Invariance of the MSR action

Now let us consider the MSR action (7.1.13) for this Langevin dynamics:

A[ψ,

ψ]=





(t)β

−1

(t) + i

(t)



∂ψ

∂t

−

[ψ]−L

δF

δψ

(t)



(A7.3.1)

The time-reversal property of the MSR action A[ψ,

ψ] depends on how the ﬁelds ψ and

ψ change under T . While the change for ψ is given by eqn. (A7.3.1), we need to specify

the change for

ψ. For this we note that the action functional A involves, apart from ψ

and

, the functional derivative δF/δψ

. Therefore we use the following prescription for

(t) =

(−t) =−κ



(t) − γ



δF

δψ



, (A7.3.2)

356 Appendix to Chapter 7

where κ and γ are open parameters that can be chosen so as to control the behavior of A

under T . We now consider using (A7.3.1) and (A7.3.2), the effect of time reversal on the

MSR action:

TA= β

−1





(−t) − γ



δF

δψ



−t





(−t) − γ



δF

δψ



−t



+i κ





(−t) − γ



δF

δψ



−t







∂ψ

(−t)

∂(−t)

−



[ψ(−t)]+L





δF

δψ



−t



= β

−1

+i κI

. (A7.3.3)

The two integrals I

and I

are evaluated in the following forms:



dt L



− 2γ



δF

δψ



+ γ



δF

δψ



δF

δψ



−t

(A7.3.4)

and





∂ψ

∂t

−

(

[ψ]+L

)

δF

δψ

4

−t

− γ





δF

δψ



∂ψ

∂t



−t

+ γ





δF

δψ

[ψ]+L

δF

δψ



−t

= I



+ J

, (A7.3.5)

where we have denoted on the RHS of both equations by use of the subscript “−t” that the

ﬁelds ψ and

ψ within the square brackets are evaluated at time −t. We ﬁrst evaluate the

integrals J

, and J

=−γ





δF

δψ

∂ψ

∂t



−t

=−γ



−t

∂ F

∂t

=−γ

−t

− F

−t

, (A7.3.6)

= γ





δF

δψ

[ψ]

δF

δψ



−t

. (A7.3.7)

In evaluating J

we have used the fact that





δF

δψ

[ψ]

δF

δψ



−t

= 0, (A7.3.8)

A7.4 The memory-function approach 357

since Q

is odd under the exchange of i and j.Usingeqns. (A7.3.6) and (A7.3.8) in eqn.

(A7.3.5), we obtain for the integral I

the result





∂ψ

∂t

−

(

[ψ]+L

)

δF

δψ

4

−t

− γ

−t

− F

−t

+ γ





δF

δψ

[ψ]

δF

δψ



−t

. (A7.3.9)

Using the results of (A7.3.4) and (A7.3.9),ineqn. (A7.3.3), we obtain

TA[ψ,

ψ]=κ





−1

−t

− γ

−t

− F

−t



iκ



∂ψ

∂t

− Q

[ψ]

δF

δψ

+i {2iβ

−1

κγ − 1}L

δF

δψ



−t

+ (iκγ + β

−1

)





δF

δψ

[ψ]

δF

δψ



−t

. (A7.3.10)

We now adjust the parameters so that the MSR action remains invariant under the transfor-

mation T . We therefore require that

= 1, 2iβ

−1

κγ − 1 = 1, i κγ + β

−1

= 0. (A7.3.11)

More speciﬁcally, we choose κ =−1 and β

−1

γ = i so that

TA[ψ,

ψ]=



−t



−1



∂ψ

∂t

−

[ψ]−L

δF

δψ



−

−t

− F

−t

= A[ψ,

ψ]+

−t

− F

−t

, (A7.3.12)

since ﬁnally we take the limit t

=−t

→∞. This makes the transformation T which

leaves the MSR action invariant (up to a constant) as follows:

(x, −t) → 

(x, t), (A7.3.13)

(x, −t) →−



(x, t) − iβ

δF

δψ

(x, t)



. (A7.3.14)

If F is a non-Gaussian functional of the ﬁelds {ψ

} then the above transformations which

leave the MSR action invariant are nonlinear.

A7.4 The memory-function approach

We present below an alternative deduction of the mode-coupling model using the

projection-operator method.

358 Appendix to Chapter 7

A7.4.1 The projection-operator method

The projection-operator scheme provides us with a way of describing the dynamics of a

many-particle system in terms of a reduced set of variables, given a proper deﬁnition of

their inner product. In the present context of the dynamics of ﬂuids, we use the set of local

densities of the conserved properties of mass, momentum, and energy to constitute the

chosen set of slow modes. The average w.r.t. equilibrium ensemble is taken as the inner

product. In general, for the deterministic equations of hydrodynamics the conserved densi-

ties refer to the corresponding ﬂuctuating quantity averaged over some suitable statistical

ensemble. The projection-operator technique, on the other hand, constructs the equations

of motion which apply to the time evolution of the corresponding ﬂuctuating property in

any single member of the ensemble.

Let us consider a set of dynamic variables {A

(r, t)} whose time evolution follows from

the Liouville equation,

∂ A

∂t

+ LA

= 0, (A7.4.1)

involving the Liouville operator L (Hansen and McDonald, 1986). The formal solution

of the above equation gives A

(t) = exp(iLt) A

. We deﬁne A

such that its equilibrium

average is equal to zero and use the notation A

(t = 0) ≡ A

. The correlation function C

of the variables A

is deﬁned as

(t) =

∗

(t) A

(0)

, (A7.4.2)

where the angular brackets denote an average over the equilibrium distribution. The pro-

jection operator P is deﬁned through its action on a dynamic variable B(t),

P B(t) =



j,k

B(t)A

∗

−1

. (A7.4.3)

The operator

Q = 1 −P (A7.4.4)

denotes the projection in the orthogonal subspace. The projection operator satisﬁes the

properties

= P, Q

= Q, PQ = QP = 0. (A7.4.5)

Next we make use of the following operator identity:

itL

= e

itQL



ds e

i(t−s)L

PLe

isQL

. (A7.4.6)

The above identity is proved easily by taking the Laplace transform of the RHS and then

applying the convolution theorem. Deﬁning the Laplace transform of a function f (t) as

f (z) = (−i)



∞

dt e

izt

f (t), Im(z)>0, (A7.4.7)

A7.4 The memory-function approach 359

we obtain

z + QL

−

z + L

z + QL

−

z + L

{

L − QL

}

z + QL

z + L



z + L − L + QL

z + QL



z + L

. (A7.4.8)

The ﬁnal expression reached is the Laplace transform of the LHS of (A7.4.6).Nextwe

operate with both sides of this operator identity on QL A

. The LHS gives, using Q =1 −P,

itL

QLA

= e

itL

− e

itL

PLA

∂

∂t

itL

A −e

itL

(LA

∗

−1

∂ A

(t)

∂t

−

(LA

∗

−1

(t). (A7.4.9)

In eqn. (A7.4.9) we have used the fact that the averaged quantities are independent of

phase-space variables and the operator L does not act on them. Using the identity (A7.4.6)

for e

itL

on the LHS,

(t) +



ds e

i(t−s)L

(LR

(s)) A

∗

−1

= R

(t) +



(LR

(s)) A

∗

A



−1

(t − s), (A7.4.10)

where we have deﬁned

(t) = e

itQL

QLA

= e

itQLQ

QLA

. (A7.4.11)

We have used the property (A7.4.5) of the operator Q in reaching the last equality. There-

fore, on equating the two sides of eqn. (A7.4.9), an equation for the time evolution of the

dynamic variables A

(t) is obtained in the following matrix form:

A(t) − i  · A(t) +



M(t − s) · A(s)ds = R(t). (A7.4.12)

A refers to a column vector with the A

, i = 1,..., n (say) as elements.  is the n × n

frequency matrix. Using the anti-Hermitian nature of the operator L, the matrix elements



are obtained as





∗

iL A

∗

−1

. (A7.4.13)

R is a column matrix with elements R

(i = 1,..., n) given by eqn. (A7.4.11).

Equation (A7.4.12) is in fact a simple consequence of the Liouville equation arranged

in a different form. The construction of this mathematical identity involves the projection

operator P, which is based on a suitably chosen inner product. Its physical meaning is clear

only when we interpret this equation as a Langevin equation for a set of “slow” variables

}. The many remaining degrees of freedom other than {A

} for the system are spanned

360 Appendix to Chapter 7

by the operator Q. Their role in the dynamics is given by R

(t) in (A7.4.12), and they are

treated as “noise.” The identiﬁcation of this equation with the Langevin equation (A7.4.12)

is therefore closely linked to R

(t) having the characteristics of the Langevin noise with

respect to the slow variables {A

}. The average of the noise over the initial nonequilibrium

ensemble must be zero. Using the maximum-entropy principle, similarly to what we did in

the case of the equilibrium ensemble, we write the nonequilibrium distribution 



(, 0) = 

()

1 + μ

∗

() +···

, (A7.4.14)

where the {μ

} represent the Lagrange multipliers to be determined in terms of the corre-

sponding averages A

 in the nonequilibrium ensemble. Using (A7.4.14), we obtain for

the average of the noise over the initial nonequilibrium ensemble

R

(t)=



d R

(t)

()

⎡

⎣

1 +



∗

() + O(μ

)

⎤

⎦

. (A7.4.15)

The ﬁrst term on the RHS gives a vanishing contribution, since for the equilibrium state,

for any time,

A(t)=A

= 0, (A7.4.16)

and hence, from the equation of motion, we obtain

R

(t)

= 0. (A7.4.17)

For the second term on the RHS to vanish we must have

R

(t)=



d R

(t)

()A

∗

() = 0. (A7.4.18)

At this point the equilibrium average is taken as the inner product in the deﬁnition of the

projection operator. This identiﬁcation ensures that the noise average is zero to linear order

in deviation from the equilibrium, with R

(t) remaining orthogonal to the space of A at all

times,

∗

(t)

= 0. (A7.4.19)

The kernel matrix M in (A7.4.12) links the dynamics of A to its values at earlier times and

is termed the memory-function matrix. M is expressed in terms of the correlation of the

force R(t ) in the orthogonal subspace of Q. The correlation function in the second term on

the RHS of (A7.4.10) is simpliﬁed using the anti-Hermitian nature of L,

(LR

(s)) A

∗

=−R

(s)(L A

)

=−R

(s)(1 −P)(LA

). (A7.4.20)

In obtaining the last equality, we have made use of the property

R

(s)P(LA

)=0, (A7.4.21)