Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond
Подождите немного. Документ загружается.


7.3 Renormalization 341
The renormalized theory takes a simpler form in the hydrodynamic limit of small wave
number and frequency. In the transverse case in which the hydrodynamic modes are diffu-
sive the self-energies
T
(q,ω) are analyzed for ω ∼ q
2
in the limit of small q. In doing
the analysis in this limit, we first identify the explicit factors of q and ω in the different
self-energies necessitated by symmetry and conservation laws. We have, for example, that
T
ˆgv
=−iq
2
γ
T
ˆgv
(q,ω), (7.3.38)
T
ˆg ˆg
=−q
2
γ
T
ˆg ˆg
(q,ω), (7.3.39)
T
ˆg ˆv
=−iq
2
γ
T
ˆg ˆv
(q,ω). (7.3.40)
As a consequence of conservation of momentum, every external ˆg
i
vertex contribution to
T
ˆgv
supplies a factor of q
i
. Since the system is isotropic, all of the
T
ˆgβ
then must be of
O(q
2
). Using the fluctuation–dissipation theorem the following nonperturbative relations
between the self-energies are obtained (Das and Mazenko, 1986) in the hydrodynamic
limit:
γ
T
ˆg ˆg
(0, 0) = 2β
−1
γ
T
ˆgv
(0, 0), (7.3.41)
T
ˆv ˆv
(0, 0) = 2β
−1
ω
−1
T
ˆvv
(0,ω). (7.3.42)
The last equation presented above tells us that
T
ˆvv
(0, 0) = 0 since
T
ˆv ˆv
(0, 0) is nonzero
and finite. Therefore, in the hydrodynamic limit we can write down the transverse corre-
lation functions in the same form as the corresponding zeroth-order quantity obtained for
those in the Gaussian action, with the renormalized viscosity being given in terms of
η
R
=
η
0
+ γ
ˆgv
(0, 0)
ρ
T
−1
(7.3.43)
or, in terms of the ˆg ˆg self-energy, as
η
R
=
η
0
+
β
2
γ
ˆg ˆg
(0, 0)
ρ
T
−1
, (7.3.44)
where
ρ
T
= ρ
0
+
T
ˆvv
(0, 0). (7.3.45)
The results (7.3.43) and (7.3.44) indicate that, in the hydrodynamic limit, the transverse
correlation and response functions corresponding to the dynamics with the full nonlinear-
ities are obtained in terms of the renormalized (generalized) shear viscosity. The renor-
malization of the latter is obtained from either the correlation self-energy (involving both
hatted field indices)
T
ˆg ˆg
or equivalently from the response self-energy (involving a single
hatted field index)
T
ˆgv
. This result is a direct consequence of the fluctuation–dissipation
result (7.3.29).

342 Renormalization of the dynamics
The longitudinal case
The longitudinal case is somewhat more complicated than the transverse one since here
we have to deal with three fields {ρ,g, v} both in the hatted and in the unhatted sets. The
correlation functions are obtained by inverting the longitudinal part of the G
−1
matrix. The
response functions are presented in the form (7.2.34). The fluctuation–dissipation theorem
(7.3.29) once again is used to link the response function to the correlation function similarly
to what we have already discussed in the transverse case. The crucial relation used in this
regard is given by (7.2.31). In the longitudinal case there are traveling modes and hence the
self-energies
L
are analyzed in the limit ω ∼ q as q → 0. We first define the self-energy
elements in terms of the explicit factors of q and ω necessitated by conservation laws and
symmetry. We have, for example, that
L
ˆg ˆg
=−q
2
γ
ˆg ˆg
, (7.3.46)
L
ρ ˆv
= qγ
ρ ˆv
, (7.3.47)
L
ˆgv
=−iq
2
γ
ˆgv
, (7.3.48)
ρ ˆg
= qγ
ρ ˆg
. (7.3.49)
Relations between the different elements of the self-energy matrix follow directly from
the analysis of the fluctuation–dissipation theorem (Das and Mazenko, 1986). We will
discuss here two results that are particularly useful for our subsequent analysis of the
self-consistent mode-coupling theory. First, we consider the relation between the matrix
elements which are involved in the renormalization of the viscosity,
γ
ˆg ˆg
(0, 0) = 2β
−1
γ
ˆgv
(0, 0) +˜γ
ρ ˆg
, (7.3.50)
where we have defined the limiting quantity
˜γ
ρ ˆg
= lim
ω→0
ω
−1
γ
ρ ˆg
(0,ω). (7.3.51)
The renormalization of the longitudinal viscosity
0
is computed in terms of the response
self-energy
ˆgv
as
L(q,ω) =
0
+ γ
ˆgv
(0, 0) +˜γ
ρ ˆg
ρ
−1
L
(7.3.52)
or in term of the correlation self-energy
ˆg ˆg
as
L(q,ω) =
0
+
β
2
γ
ˆg ˆg
(0, 0)
ρ
−1
L
, (7.3.53)
with ρ
L
given by
ρ
L
= ρ
0
+
ˆvv
(0, 0). (7.3.54)
Thus for both the shear and the longitudinal viscosities the renormalization can be com-
puted by analyzing either
ˆg ˆg
or the response self-energies
ˆgv
and
ˆgρ
. We have there-
fore established nonperturbatively the renormalizability of the theory in the hydrodynamic

7.3 Renormalization 343
limit. This is obtained using only the fluctuation–dissipation theorem (7.3.29). In this limit
of small ω and q the renormalization of the full correlation functions involves the replace-
ments c
0
→ c and
0
→ L(q,ω)in the zeroth-order expressions. Since both
ˆvv
(0, 0) and
ρ ˆg
(0, 0) vanish in the hydrodynamic limit, the renormalized quantities ρ
L
and c are real.
Finally, we consider a useful relation for the self-energy matrix element
ˆvρ
. Note that
the latter involves the nonlinear vertex concerning the conjugate field ˆv. This vertex is a
consequence of the nonlinear constraint (6.2.22) introduced in the theory to deal with the
1/ρ nonlinearities in the dynamics,
ˆv ˆv
(0, 0) =
2ρ
L
βc
2
γ
ρ ˆv
(0, 0), (7.3.55)
where the renormalized speed of sound is given by c
2
= c
2
0
− γ
ρ ˆg
(0, 0). This result
also follows from the analysis of the fluctuation–dissipation theorem (7.3.29) in the hydro-
dynamic limit.
7.3.3 One-loop renormalization
We now consider the renormalization of the transport coefficients at one-loop order. This
calculation in a natural way gives rise to the self-consistent mode-coupling model which
forms the basis of our discussion in the subsequent chapters on equilibrium and nonequi-
librium dynamics in the glassy state. The MSR action A for the specific case of the
compressible liquid can now be written from (7.2.8) in the symmetrized form
A[ψ,
ˆ
ψ]=
1
2
d1
d2
α,β
ψ
α
(1)
G
0
αβ
−1
(12)ψ
β
(2)
+
1
3
d1
d2
d3
αβγ
V
αβγ
(123)ψ
α
(1)ψ
β
(2)ψ
γ
(3)
+
1
4
d1
d2
d3
d4
αβγ μ
V
αβγ μ
(1234)ψ
α
(1)ψ
β
(2)ψ
γ
(3)ψ
μ
(4),
(7.3.56)
where the repeated indices α, β, γ , and μ in all three terms are summed over. We adopt
a notation in which we denote the different fields as ψ
α
(1) with the index 1 represent-
ing the space-time point (x
1
, t
1
), where α represents the corresponding slow variable and
runs over ρ, ˆρ, g
i
, ˆg
i
,v
i
, and ˆv
i
. Let us focus on the non-Gaussian part of the action. The
symmetrized cubic vertices in the action (7.3.56) are obtained as
V
αβγ
(123) =
1
2
˜
V
αβγ
(123) +
˜
V
βαγ
(213) +
˜
V
αβγ
(321)
+
˜
V
αγβ
(132) +
˜
V
βγα
(231) +
˜
V
γαβ
(312)
, (7.3.57)

344 Renormalization of the dynamics
where
˜
V
αβγ
(123) =
3
i=1
˜
V
(i)
αβγ
(123). (7.3.58)
ThelastlineontheRHSofeqn. (7.3.56) represents a four-point vertex function. This arises
from the convective nonlinearity ∇
j
[g
i
g
j
/ρ]≡∇
j
(ρv
i
v
j
) in the equation of motion for
the momentum density.
From the polynomial form of the action discussed in the previous section the vertex
functions are obtained. Specifically, for the flat-structure-factor case,
˜
V
(1)
αβγ
(123) = i
i
δ
α, ˆg
i
∇
i
1
χ
−1
2
δ(1, 2)δ(1, 3)δ
β,ρ
δ
γ,ρ
, (7.3.59)
˜
V
(2)
αβγ
(123) = iρ
0
i, j
δ
α, ˆg
i
∇
i
1
δ(1, 2)δ(1, 3)δ
β,v
i
δ
γ,v
j
, (7.3.60)
˜
V
(3)
αβγ
(123) =−i
i
δ
α, ˆv
i
δ
β,ρ
δ
γ,v
i
. (7.3.61)
The vertices presented above arise from the pressure term, the convective term in the
generalized Navier–Stokes equation (6.2.20), and the nonlinear constraint (6.2.22), respec-
tively. Similarly the quartic vertex is a sixth of the sum of all permutations of the vari-
ables (α, 1), (β, 2), (γ , 3), and (μ, 4) labeling the unsymmetrized vertex
˜
V
αβγ μ
(1234),
where
˜
V
αβγ μ
(1234) = i
i, j
δ
α, ˆg
i
δ
β,ρ
δ
γ,v
i
δ
μ,v
j
∇
i
1
[δ(1, 2)δ(1, 3)δ(1, 4)]. (7.3.62)
The role of these four-point vertices with respect to the long-time tails in viscosities has
already been indicated in Section 6.1.1. In three-dimensional systems the contributions
from such terms can be taken into account through a redefinition of the bare transport
coefficient. In the following we ignore this nonlinearity. Using the above expressions for
the vertex functions, the different elements of the self-energy matrix are obtained in
a self-consistent form in terms of the full correlation function from the formula (7.1.28).
This has so far been achieved only at one-loop order.
We saw in the earlier section that the renormalizations of the viscosities
0
(longitudinal)
and η
0
(shear) are obtained from the corresponding components of the self-energy
ˆg
i
ˆg
j
.
A detailed diagrammatic analysis of the corresponding self-energy diagrams (shown in
Fig. 7.1) gives the renormalized longitudinal viscosity at one-loop order as
L(q, z) =
0
+
dt e
izt
MC
(q, t)
=
0
+
∞
0
dt e
izt
dk
(2π)
3
V
L
MC
(q, k)G
ρρ
(k, t)G
ρρ
(q − k, t), (7.3.63)
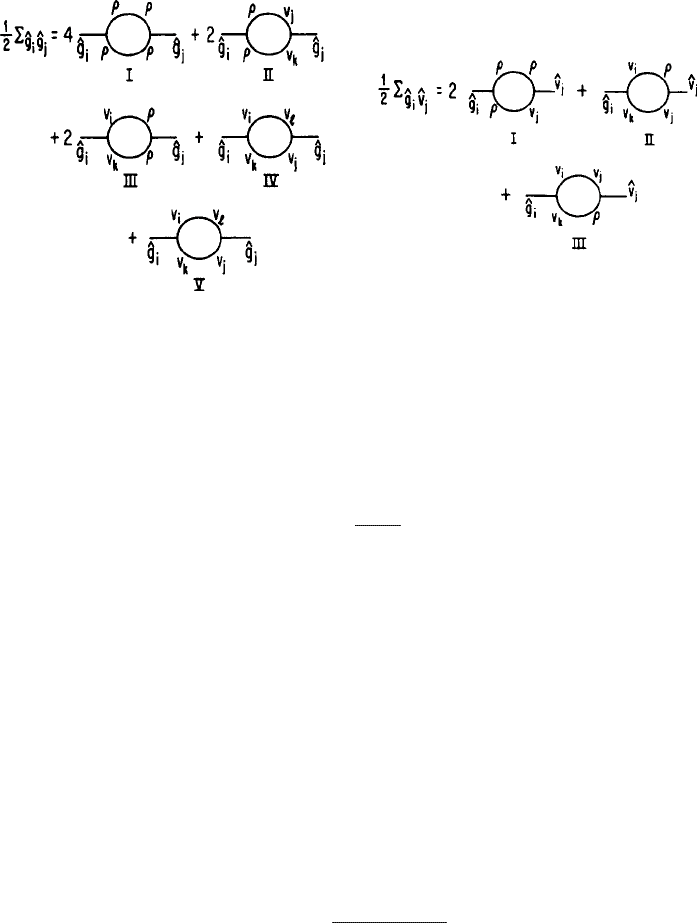
7.3 Renormalization 345
Fig. 7.1 The one-loop diagrams at O(k
B
T ) for the self-energy
ˆg
i
ˆg
j
. The lines joining both ends
with the vertices represent fully renormalized correlation functions as labeled. The vertices with three
legs attached to them are as indicated in (7.3.59)–(7.3.61).
where V
L
MC
(q, k) denotes vertex functions determined in terms of thermodynamic prop-
erties of the liquid. For example, in the wave-vector-independent model with the form
(7.3.59) we obtain
V
L
MC
≡
βχ
−2
2ρ
0
. (7.3.64)
It is important to note that the above one-loop correction to the longitudinal viscosity
is obtained with some simplifications and approximations. In the supercooled state the
slow decay of the density fluctuations is assumed to produce the dominant contribution
to the transport properties. The contributions to
ˆg ˆg
from diagrams involving the convec-
tive vertices (resulting from nonlinear coupling of currents in the equations of motion) are
relatively small in the supercooled state and are absorbed by redefining the corresponding
bare transport coefficient. This is a key approximation made in the study of slow dynamics
using the mode-coupling models.
3
The renormalized density correlation function
A key quantity of interest in all subsequent discussions will be the density–density correla-
tion function. We define the normalized correlation function with respect to the equal-time
value as
ψ(q, t) =
G
ρρ
(q, t)
G
ρρ
(q, t = 0)
. (7.3.65)
The renormalization is easily extended to the case in which a realistic structure factor with
a proper wave-vector dependence is taken into account. With the wave-vector-dependent
3
This approximation is further justified with the dynamic density-functional model. This is formulated in terms of the density
only and the momentum density is integrated out of the model using the adiabatic approximation. The renormalized theory in
this case has a very similar wave-vector dependence to that obtained above ignoring the role of the convective nonlinearity.
This is discussed later in Section 8.1.6.
346 Renormalization of the dynamics
model in which the dynamics is given by eqns. (6.2.28) and (6.2.29), the renormalized
transport coefficient L(q, z) is obtained from the relevant set of self-energies. The latter
are expressed in terms of the correlation functions and response functions. A renormalized
perturbation expansion for the transport coefficients at arbitrary order in the nonlineari-
ties can thus be constructed in principle. The renormalized longitudinal viscosity with the
mode-coupling contribution at one-loop order is given by
L(q, z) =
0
+
∞
0
dt e
izt
dk
(2π)
3
V
L
q,k
ψ(k, t)ψ(q − k, t ), (7.3.66)
where
0
is the bare viscosity. The vertex function V
L
q,k
is determined in terms of the
thermodynamic properties of the liquid as
V
L
q,k
=
n
0
2mβ
dk
(2π)
3
!
(
ˆ
q · k)c(k) +
ˆ
q · (q − k)c(|q − k|)
"
2
S(k)S(|q − k|), (7.3.67)
where S(q) denotes the static structure factor for the liquid. Using the renormalizability of
the nonlinear theory (in the hydrodynamic limit) which was proved in the previous section,
the density correlation function is obtained using the renormalized transport coefficient
L(q, z) in the expression given in eqn. (7.2.20),
ψ(q, z) =
z −
2
q
z + iq
2
L(q, z)
−1
, (7.3.68)
where
q
represents a microscopic frequency characteristic of the liquid state. Similarly,
the normalized transverse current correlation function φ
T
(q, z) takes the form
φ
T
(q, z) =
1
z + iq
2
η
R
(q, z)
, (7.3.69)
with the renormalized shear viscosity η
R
(q, z) obtained as
η
R
(q, z) = η
0
+
dt η
MC
(q, t)e
izt
. (7.3.70)
For the wave-vector-dependent model, the mode-coupling contribution η
MC
obtained from
the transverse part of the self-energy
ˆg ˆg
at one-loop order is
η
MC
(q, t) =
1
2βρ
0
dk
(2π)
3
V
T
q,k
G
ρρ
(k
1
, t)G
ρρ
(k, t). (7.3.71)
The vertex function V
T
q,k
is obtained as
V
T
q,k
=
[
c(k) − c(k
1
)
]
2
{1 − (
ˆ
q ·
ˆ
k)
2
}. (7.3.72)
Another simple and systematic approach to computing the memory function was taken
by (Zaccarelli et al., 2001) by considering the equation for ρ
q
(Fourier transform of density
ρ(x, t)). This is obtained in the form of a linear equation
¨ρ
q
+
2
q
ρ
q
(t) +
t
o
L
q
(t − s) ˙ρ
q
(s)ds = f
q
(t). (7.3.73)
7.3 Renormalization 347
A self-consistent expression for the memory function L
q
is obtained in terms of a nonlin-
ear function of ρ
q
s exploiting the proper fluctuation–dissipation relation. The final form
(8.1.33) is reached here by assuming that the noise f
q
is an additive Gaussian process. A
similar approach was used by Wu and Cao (2003) for obtaining the memory kernel for a
linear molecular liquid.
Note that in the wave-vector-dependent models the length scales over which the fluctu-
ations are considered are very small. Near the static structure-factor peak the length scale
is of the order of the diameter of a constituent particle. This involves extending the the-
ory to much shorter length and time scales beyond the hydrodynamic limit. This is the
regime of generalized hydrodynamics. It is, however, important to note that the validity
of the renormalized perturbation theory in terms of correlation functions has so far been
established only in the hydrodynamic limit, and the extension of the equations of fluctu-
ating nonlinear hydrodynamics to large wave vector is merely a plausible assumption at
this point. At high densities the mean free path of the liquid particles is small and hence
the validity of hydrodynamics is pushed to short length scales. Both in the field-theoretic
model and in the so-called memory-function approach (discussed in Appendix A7.4)the
wave-vector dependence of the vertex functions at large k involves invoking this limit. This
indeed goes back to the very basic problem of extending the dense-liquid-state theory to
the finite-wave-number and -frequency limit.
Recently a fundamental theory for the kinetics of systems of classical particles has been
presented (Mazenko, 2010). This involves a unification of kinetic theory, Brownian motion,
and the MSR field theory. Here, instead of following the standard method of constructing
the field theory with the conserved densities, one works with the microscopic equations of
motion. It is the dynamic generalization of the functional theory of fluids in equilibrium.
In this model the conjugate set of (hatted) MSR fields is introduced at the microscopic
level and the perturbation theory is organized self-consistently in terms of the interaction
potential. At the second order, the renormalized equations for the density correlation func-
tions constitute a dynamic feedback mechanism and give rise to the ergodic–nonergodic
(ENE) transition. This is very similar to ENE transition in the standard mode-coupling
theory to be discussed in the next chapter. While the model with microscopic Brownian
dynamics applies naturally to colloidal systems, the approach in general allows for com-
patible approximations for higher-order correlation functions and is in fact applicable to
a large set of dynamical systems. These include reversible and dissipative systems with
Newtonian and Fokker–Planck dynamics.
To summarize, we have obtained here, using the field-theoretic approach, the expres-
sions for the density–density correlation in terms of generalized transport coefficients,
including the effects from the coupling of the slow modes. The MSR field-theoretic model
presents a suitable technique by which to obtain the renormalized perturbation theory in
a self-consistent form. In the next chapters we discuss how this self-consistent model is
used for understanding the slow dynamics characteristic of the dense liquid approaching
vitrification.

Appendix to Chapter 7
In this Appendix we present a simple deduction (Kawasaki, 1995) for the basic model of
mode-coupling theory without going into many technical complications. In the following,
we simplify the notation by writing the vectors q ≡ q etc. The two basic equations of
nonlinear fluctuating hydrodynamics (6.2.16) and (6.2.28) are written in the simplified
form
∂ρ
∂t
+∇.g = 0(A7.1)
∂g
i
∂t
+∇
i
dx
U (x, x
)δρ(x
, t) −
j
dx
L
0
ij
(x − x
)
g
j
(x
, t)
ρ
0
+
dx
1
dx
2
V
i
(x, x
1
, x
2
)δρ(x
1
, t)δρ(x
2
, t) = f
i
(x, t). (A7.2)
First, we ignore the convective nonlinearity involving products of the momentum field g
i
from the momentum equation (6.2.28) and focus on the role of density couplings rele-
vant for the supercooled liquid. Second, we simplify the dissipative term in the momentum
equation by taking the bare transport coefficient matrix as diagonal, i.e., L
0
ij
(x − x
) ∼
ρ
0
B
δ
ij
∇
2
δ(x −x
), and ignore the 1/ρ nonlinearity produced by the corresponding equi-
librium quantity 1/ρ
0
. The noise f
i
(x, t) is related to the bare transport matrix through the
FDT relation
f
i
(r, t) f
j
(r
, t
)=2k
B
TL
0
ij
(r, r
)δ(t − t
). (A7.3)
On taking the divergence of eqn. (A7.2) and combining with the continuity equation (A7.1),
we obtain a second-order equation for the density fluctuation as
∂
2
ρ
∂t
2
−
1
βm
∇
2
dx
S
−1
(x − x
)δρ(x
, t) +
B
∂ρ(x
, t)
∂t
+∇.
dx
1
dx
2
V
i
(x, x
1
, x
2
)δρ(x
1
, t)δρ(x
2
, t)
= θ(x , t), (A7.4)
348

Appendix to Chapter 7 349
where the random noise is defined in terms of the divergence θ(x, t) =∇. f
i
(x, t).The
first term on the RHS of eqn. (A7.4) involves the inverse of the two-point function S(r),
whose Fourier transform is the static structure factor S(k).Usingeqn. (6.2.29),itfollows
that the latter is related to the Fourier transform of the two-point direct correlation function
c(k) through the Ornstein–Zernike relation S(k) = (1 − n
0
c(k))
−1
. On taking a Fourier
transform of eqn. (A7.4), we obtain
∂
2
∂t
2
+
B
q
2
∂
∂t
+
2
q
ρ
q
(t) + R
q
(t) = θ(q, t), (A7.5)
where ρ
q
(t) and θ(q, t), respectively, denote the Fourier transforms of the density fluctu-
ation δρ (r) and the noise θ(x, t).
q
= 1/
√
βmS(k) represents a microscopic frequency
of the liquid state. The linear terms in the above equation represent damping of density
fluctuations controlled by the bare transport coefficient
B
. The nonlinear term R
q
in the
above equation is obtained using the expression (6.2.30) for V
i
as
R
q
(t) =
1
βm
dk
(2π)
3
q.kc(k) + q.(q − k)c(q −k)
ρ
k
ρ
q−k
. (A7.6)
In order to obtain the renormalization of the dynamics due to R
q
we interpret the latter as
a sum of two terms,
R
q
(t) =−
t
0
dt
R
(q, t − t
)
∂ρ
q
(t
)
∂t
+
˜
θ(q, t), (A7.7)
where the first term on the RHS is a regular contribution representing memory effects in
terms of a kernel function
R
(t) and the second is the random component
˜
θ. Note that,
for a memory function with the property
R
(t) =
R
(−t), the first term remains invariant
under time reversal. Indeed, the source of the nonlinear term R
q
is from the reversible part
of the dynamics. The random part
˜
θ defined in eqn. (A7.7) is related to the corresponding
dissipative part involving
R
through the fluctuation–dissipation relation
R
(q, t) =
˜
θ(q, t)
˜
θ(−q, 0)|ρ
q
|
2
−1
. (A7.8)
Using the definitions (A7.6) and (A7.7) in the relation (A7.8), it is straightforward to
show that
R
(q, t) =
1
2ρ
0
β
dk
(2π)
3
q.kc(k) + q.(q − k)c(q −k)
2
S(k)S(q − k)
× φ
k
(t)φ
q−k
(t), (A7.9)
where φ
k
(t) is the normalized density correlation function defined as φ
k
(t) =(ρ
q
)(t)
ρ
−q
(0)|ρ
q
|
2
−1
. In reaching eqn. (A7.9) one needs to make the crucial approximation
of equating four-point correlations of density fluctuation to products of two-point density
correlation functions (see Appendix A7.4.2). This closes the mode-coupling equation at
the lowest level. Using eqn. (A7.8) in eqn. (A7.5), we obtain a second-order differential
equation for ρ
q
(t). On multiplying this equation by ρ
−k
(0) and averaging with respect

350 Appendix to Chapter 7
to the noise θ we obtain the following differential equation for the normalized density
correlation function:
¨
φ
q
(t) +
2
q
φ
q
(t) +
B
˙
φ
q
(t) +
t
0
dt
R
(q, t − t
)
˙
φ
q
(t
) = 0, (A7.10)
where
R
(t) is given by eqn. (A7.9). The above equation for φ
q
(t) constitutes the basic
equation for the mode-coupling model discussed in Chapter 8 for the ergodicity–
nonergodicity transition.
A7.1 The Jacobian of MSR fields
In obtaining the action in terms of the physical field ψ and its hatted conjugate
ˆ
ψ in the
MSR field theory we treat as constant the functional Jacobian which appears in the calcu-
lation of the generating function for computing statistical averages. More specifically, the
Jacobian is associated with the functional delta function which ensures that the field vari-
able ψ is a solution of the equation of motion. Thus the Jacobian links the field variable ψ
with the noise θ through the equation of motion for the field variable. It therefore naturally
depends on the manner in which the equation of motion is discretized in time. To explain
this, let us consider a one-dimensional case (Jensen, 1981) of a single variable ψ:
∂ψ(1)
∂t
=−
U
1
[1]+U
2
[1
¯
2]ψ(
¯
2) + W
3
[1
¯
2
¯
3]ψ(
¯
2)ψ(
¯
3)
+ θ(1), (A7.1.1)
where we adopt the convention that the repeated (barred) indices are summed or integrated
over. On a discrete-time grid the above equation of motion is written in the form (for
example)
1
!
ψ(t
i
) − ψ(t
i−1
)
"
= a
1
U
1
[t
i
]+b
1
U
1
[t
i−1
]+···
+ a
n
U
n
[t
i
, t
¯
2
,...,t
¯n
]ψ(t
¯
2
)...ψ(t
¯n
)
+ b
n
U
n
[t
i−1
, t
¯
2
]ψ(t
¯
2
). . .ψ(t
¯n
) +···+( ˜aθ
i
+
˜
bθ
i−1
), (A7.1.2)
with the constraint that the numbers a
i
and b
i
for all i satisfy a
i
+ b
i
= 1 and ˜a +
˜
b = 1.
The discretization scheme is arbitrary with these constraints and in the limit → 0we
expect that all of them should become identical. In the one-dimensional case, for example,
if we choose, for all i, a
i
= 0 and b
i
= 1, then the Jacobian is a constant,
J =
%
i∈
d+1
1
≡ C
0
. (A7.1.3)
Although in the → 0 limit C
0
is diverging, it is canceled out by a similarly large quantity
from the denominator in the final expression for a statistically averaged quantity. In general
the arbitrariness in the discretization of the equation of motion can be used to set the
Jacobian J equal to a constant. What is important is to note that the Jacobian links the field
ψ at time t
i
to its values as well as that of the noise for an earlier time t
i
< t
i
. The role of
