Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond
Подождите немного. Документ загружается.


A6.1 The coarse-grained free energy 311
We have used above the notation “Tr” for the differential
Tr ≡ δr δp =
1
N !
N
%
α=1
dr
α
dp
α
h
3
, (A6.1.6)
where h is Planck’s constant. The Hamiltonian H for the fluid is written as
H =
N
α=1
p
2
α
2m
+U (r
1
, r
2
,...,r
N
), (A6.1.7)
where U is the interaction term and is a function of the spatial coordinates and r
α
is the
position of the αth particle (α = 1,...,N ) and will be simply denoted as U (r).TheRHS
of eqn. (A6.1.5) is further simplified by using integral representations for the Kronecker
delta δ
k
and the Dirac δ given, respectively, by
δ
k
ρ
a
−
N
α=1
mψ
a
(r
α
)
=
?
dz
a
2πiz
a
exp
i
ρ
a
−
N
α=1
mψ
a
(r
α
)
ln z
a
(A6.1.8)
and
δ
g
a
−
N
α=1
p
α
ψ
a
(r
α
)
=
∞
−∞
dy
a
(2π)
3
exp
iy
a
· g
a
−
N
α=1
y
a
· p
α
ψ
a
(r
α
)
, (A6.1.9)
where the integral
@
in (A6.1.8) is with ln z
a
and denotes the integral along a closed contour
around the origin (Carrier et al., 1966). On substituting the representations (A6.1.8) and
(A6.1.9) into eqn. (A6.1.5) we obtain
e
−β F
=
%
a
?
dz
a
2πiz
a
∞
−∞
dy
a
(2π)
3
exp
!
i(y
a
· g
a
+ ρ
a
ln z
a
) + φ(z, y)
"
. (A6.1.10)
The function φ(z, y) is obtained as
e
φ(z,y)
=
δr δpe
−β H
exp
−i
N
α=1
(
m ln z(r
α
) + p
α
· y(r
α
)
)
. (A6.1.11)
We have introduced above the functions ln z(r) and y(r),
ln z(r) =
a
{ln z
a
}ψ
a
(r),
y(r) =
a
y
a
ψ
a
(r). (A6.1.12)
The momentum integral in eqn. (A6.1.11) is computed by completing the perfect square
and then performing the Gaussian integral. This gives the result
e
φ(ζ)
=
1
N !
dr
1
... dr
N
exp
−βU (r) − N ln
3
0
−im
N
α=1
ln ζ(r
α
)
, (A6.1.13)
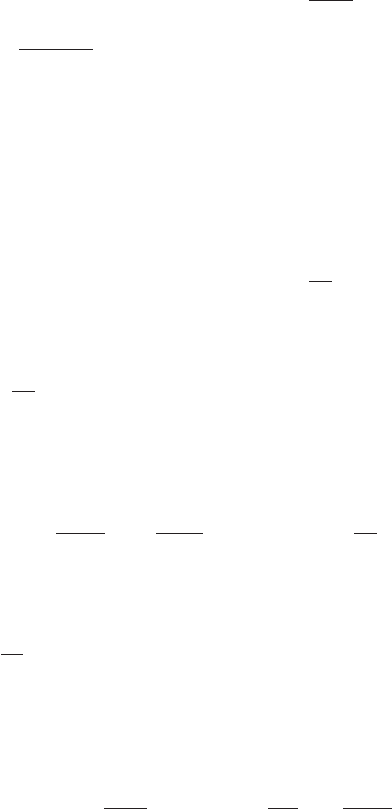
312 Appendix to Chapter 6
where
ζ(r) = z(r) exp
−i
y
2
(r)
2β
(A6.1.14)
and
0
= h/
√
2πmk
B
T is the thermal de Broglie wavelength (Huang, 1987). We identify
the variables ζ
a
for the cells, which are similar to z
a
and y
a
in eqn. (A6.1.12), in terms of
the characteristic functions ψ
a
in the following manner:
ln ζ(r) =
a
{ln ζ
a
}ψ
a
(r). (A6.1.15)
From the property (A6.1.1) it follows easily that
ln z
a
= ln ζ
a
+i
y
2
a
2β
. (A6.1.16)
Equation (A6.1.13) now reduces to the form
e
φ(ζ)
=
1
N !
dr
1
... dr
N
e
−βU(r
α
)−N ln
3
0
%
a
e
−i ln ζ
a
{m
5
α
ψ
a
(r
α
)}
. (A6.1.17)
On using eqn. (A6.1.16) in (A6.1.10) and changing the integration variable from z
a
to ζ
a
,
we obtain
e
−β F
=
%
a
?
dζ
a
2πi ζ
a
∞
−∞
dy
a
(2π)
3
exp
i
y
a
· g
a
−
ρ
a
2β
y
2
a
+ θ(ζ
a
)
, (A6.1.18)
where
e
θ(ζ
a
)
=
1
N !
dr
1
... dr
N
e
−βU(r
α
)−N ln
3
0
exp
i
&
ρ
a
− m
α
ψ
a
(r
α
)
'
ln ζ
a
.
(A6.1.19)
The variable y in eqn. (A6.1.18) is now integrated out by completing the perfect square
and performing the Gaussian integral, obtaining
e
−β F
=
%
a
β
2πρ
a
3/2
exp
−β
g
2
a
2ρ
a
?
dζ
a
2πi ζ
a
e
θ(ζ
a
)
. (A6.1.20)
The coarse-grained free energy F ≡ F[ρ(x), g(x)] is obtained by taking the continuum
limit, i.e.,
cl
→ 0 and a →∞. In this limit the cell values of the densities of mass and
momentum can be treated as continuous fields,
ρ
a
→ ρ(x)
cl
, (A6.1.21)
g
a
→ g(x)
cl
. (A6.1.22)
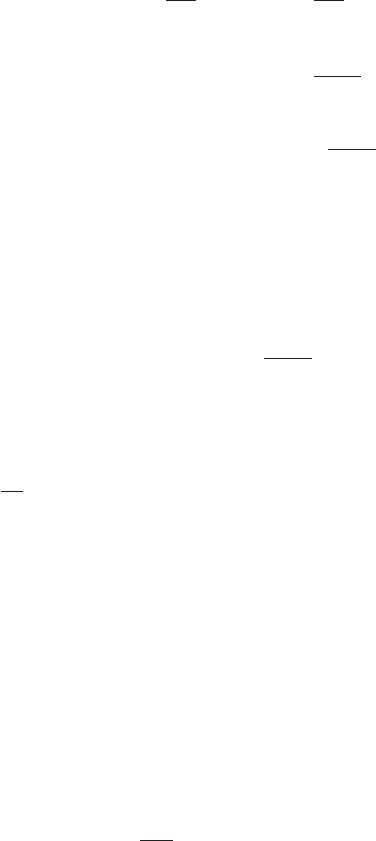
A6.1 The coarse-grained free energy 313
The momentum-density-dependent part of the free energy in the exponent on the RHS
of eqn. (A6.1.20) is now obtained in the form of a volume integral involving the field
variables,
lim
cl
→0
%
a
exp
g
2
a
2ρ
a
= exp
a
g
2
a
2ρ
a
≡ exp
a
g
2
(x)
2ρ(x)
cl
= exp
dx
g
2
(x)
2ρ(x)
. (A6.1.23)
The density-dependent part of the coarse-grained free energy is separated into two parts,
F = F
K
[ρ,g]+F
U
[ρ]. (A6.1.24)
The part F
U
[ρ] is dependent only on the density ρ, while the kinetic part F
K
is dependent
on the momentum density as well. The latter is given in units of β
−1
= k
B
T as
F
K
[g,ρ]=
dx
g
2
(x)
2ρ(x)
. (A6.1.25)
On substituting for e
θ(ζ)
from eqn. (A6.1.19), the integral in eqn. (A6.1.18) reduces to the
form
e
β F
U
[ρ]
=
1
N !
dr
1
... dr
N
e
−βU(r
α
)−N ln
3
0
%
a
δ
k
ρ
a
−
N
a=1
mψ
a
(r
α
)
.
(A6.1.26)
An approximate form of the coarse-grained form of the free-energy functional is obtained
by evaluating the integrals over the spatial variables {r
α
} in terms of occupation num-
bers {n
a
} of the cells, where n
a
= ρ
a
/m. The volume element dr
1
... dr
N
/N! with the
delta-function constraints on the RHS of eqn. (A6.1.26) is evaluated in terms of a local-
ized distribution of the particles in the cells, in which n
a
identical particles are in a given
cell of volume
cl
. The volume element is obtained as a product over the cells given by
<
a
n
a
cl
/n
a
!
. The effect of interaction between the particles is included through F
in
[{ρ
a
}]
involving the densities ρ
a
in the cells. The coarse-grained function F
U
[ρ] is written in
terms of cell contributions in the form
exp
−β F
U
[ρ]
=
%
a
n
a
cl
n
a
!
e
−N ln
3
0
exp
−β F
in
[{ρ
a
}]
. (A6.1.27)
Thus F
U
[ρ] is obtained as a sum of an ideal-gas part F
id
and an interaction contribution
F
in
,
F = F
id
+ F
in
. (A6.1.28)
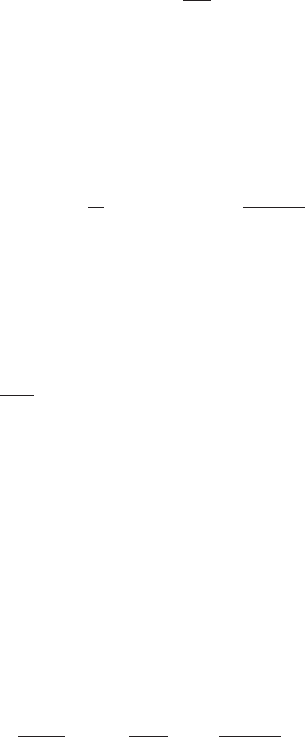
314 Appendix to Chapter 6
The ideal-gas contribution corresponding to a noninteracting system (U = 0) F
id
is
obtained from eqn. (A6.1.27) using the Starling approximation,
β F
id
=
a
n
a
ln
n
a
cl
− n
a
+ N ln
3
0
. (A6.1.29)
In the continuum limit the RHS of (A6.1.29) (using the constraint
5
a
n
a
= N) reduces to
the form
β F
id
=
a
n(x) ln
n(x)
3
0
− n(x)
cl
→
1
m
dx ρ(x)
ln
ρ(x)
3
0
m
− 1
, (A6.1.30)
where
0
is the thermal de Broglie wavelength. The above result is identical to the ideal-
gas contribution to the free energy obtained in Chapter 2. The interaction part F
in
is a
consequence of the interaction U . For example, the two-body interaction term defined in
the Hamiltonian (1.1.16) is expressed as
U [r
α
]=
1
2m
2
dx
dx
ˆρ(x
)u(x − x
) ˆρ(x
) ≡ U[ˆρ(x)] (A6.1.31)
in terms of the microscopic density functions ˆρ(x). If the coarse graining were an exact
mapping T [ρ|ˆρ] at every point, we would be able to write the interaction part defined in
eqn. (A6.1.27) above as
F
in
= U [ρ(x)]. (A6.1.32)
In reality this is the simplest approximation since the coarse graining maps the densities
over the coarse-graining volume into a smooth average function. The approximate coarse-
grained free-energy functional is therefore obtained as
F[ρ, g]=F
K
[ρ,g]+F
U
[ρ]
=
dx
g
2
(x)
2ρ(x)
+ k
B
T
ρ(x)
m
ln
ρ(x)
3
0
m
− 1
+U [ρ(x)]
(A6.1.33)
in terms of the bare-interaction-potential function.
The free-energy functional F[ρ,g,v]
We have seen that in an appropriate formulation of the dynamics of the compressible liquid
to take into account all the relevant nonlinearities a new field v enters the fluctuating-
hydrodynamics description. It is defined in terms of the nonlinear constraint
g = ρv. (A6.1.34)

A6.1 The coarse-grained free energy 315
Let us consider the implications of extending the space of coarse-grained variables to
{ρ,g,v}. The corresponding driving free-energy functional F[ρ, g,v] is connected to its
counterpart F[ρ, g] through the relation
exp
−β F [ρ,g,v]
= exp
−β F [ρ,g]
˜
[ρ · g, v], (A6.1.35)
where the free-energy functional in terms of variables {ρ,g} is obtained as F[ρ,g]=
F
K
[ρ,g]+F
U
[ρ]. The function
˜
[ρ · g, v] on the RHS of eqn. (A6.1.35) ensures that the
nonlinear constraint (A6.1.34) is maintained, i.e.,
Dg
˜
[ρ · g, v]=1. (A6.1.36)
Now we define the density-dependent function
˜
F[ρ] by integrating out the variables g and
v from the fluctuating-hydrodynamics description as
exp
−β
˜
F
U
[ρ]
=
Dg
Dv exp
{
−β F [ρ,g,v]
}
. (A6.1.37)
The multiple integral on the RHS of eqn. (A6.1.37) can be evaluated in different orders
yielding an identical result. Let us demonstrate this for consistency.
First, we integrate g. Using the explicit form of the momentum-dependent part F
K
[ρ,g]
(see eqn. (A6.1.25) above) and the definition (A6.1.36), the integral on the RHS in eqn.
(A6.1.37) reduces to the form
exp
−β
˜
F
U
[ρ]
= I
v
[ρ]e
−F
U
[ρ]
, (A6.1.38)
where I
v
[ρ] is the Gaussian integral on the RHS with respect to g,
I
v
[ρ]=
Dv exp
3
−
dx ρ(x)
v
2
(x)
2
4
. (A6.1.39)
On the other hand, we obtain, on integrating out v first,
exp
−β
˜
F
U
[ρ]
= I
0
[ρ]I
g
[ρ]e
−F
U
[ρ]
, (A6.1.40)
where the integrals I
0
[ρ] and I
g
[ρ] are defined as
I
0
[ρ]=
Dv
˜
[ρ · g, v], (A6.1.41)
I
g
[ρ]=
Dg exp
3
−
dx
g
2
(x)
2ρ(x)
4
. (A6.1.42)
For the integral I
0
we use the representation of the delta function in terms of a normalized
Gaussian function,
˜
[ρ,g, v]∼δ(g − ρv)
= lim
σ →0
1
(2πσ
2
)
3/2
exp
−
(g − ρv)
2
2σ
2
(A6.1.43)

316 Appendix to Chapter 6
We now make a change of variable v→v + g/ρ. With another change of variable v/σ→˜v
(before taking the delta-function limit of width σ going to zero), the integral I
0
reduces to
a Gaussian form
I
0
=
D
˜
v exp
−
dxρ
2
(x)
˜v
2
(x)
2
. (A6.1.44)
All three integrals I
0
, I
g
, and I
v
have the same form,
I
ϑ
[ f ]≡e
A
ϑ
[f ]
=
Dϑ exp
−
dx f
2
(x)
ϑ
2
(x)
2
. (A6.1.45)
with f (x) ∼ ρ(x), ρ
−1/2
(x) and ρ
1/2
(x), respectively. ϑ(x) is a vector field of the same
dimension as g or v. Dϑ ≡
<
i
Dϑ
i
. The integral (A6.1.45) is evaluated using the identity
Dϑ
δ
δϑ
j
(x
)
ϑ
i
(x) exp
−
dx
f
2
ϑ
2
2
, (A6.1.46)
which leads to the result
f
2
(x)
Dϑϑ
i
(x)ϑ
j
(x
) exp
−
dx
f
2
ϑ
2
2
= δ
ij
δ(x − x
)I
ϑ
. (A6.1.47)
In the limit x → x
, on setting i = j and summing over i, we obtain for d dimensions
f
2
(x)
Dϑϑ
2
(x) exp
−
dx
f
2
ϑ
2
2
= dδ(0)I
ϑ
, (A6.1.48)
where δ(0) =
6
3
/(2π)
d
for a short-wavelength cutoff of 2π/ in the theory. On the
other hand, on taking a derivative of (A6.1.45) with respect to f and using eqn. (A6.1.48),
one obtains
δI
ϑ
δ f (x)
≡ I
ϑ
[ f ]
δ A
ϑ
δ f (x)
=−f (x)
Dϑϑ
2
(x)e
−
6
dx f
2
(x)
ϑ
2
(x)
2
=−dδ(0)
I
ϑ
[ f ]
f (x)
. (A6.1.49)
On solving eqn. (A6.1.49), one obtains A
ϑ
[ f ] as
A
ϑ
[ f (x)]=−dδ(0) ln
f (x)
f
0
, (A6.1.50)
where f
0
is the value of f for which A
ϑ
[ f ]=0. I
0
, I
g
, and I
v
, respectively, correspond
to f (x) being ρ(x), ρ
−1/2
(x), and ρ
1/2
(x), and satisfy
I
0
I
g
= I
v
= exp
−
d
2
δ(0) ln
ρ(x)
ρ
0
, (A6.1.51)
rendering the RHS of eqn. (A6.1.38) and that of eqn. (A6.1.40) identical. We obtain the
result
Dg
Dv e
−β F[ρ,g,v]
= e
−β F
U
[ρ]
e
−
d
2
δ(0) ln
(
ρ(x)
ρ
0
)
, (A6.1.52)

A6.1 The coarse-grained free energy 317
which is consistent with the fluctuating-hydrodynamics description in terms of the fluc-
tuating fields {ρ,g, v}. We consider the density-dependent part as F
U
[ρ] and ignore the
second factor on the RHS of eqn. (A6.1.45). The latter is absorbed as a renormalization of
the static behavior in terms of an extra field ϑ(x),
β F [ρ,g,v,ϑ]=β F [ρ,g,v,ϑ]+
dx
ϑ
2
(x)
2ρ(x)
(A6.1.53)
so as to write
Dg
Dv
Dϑ e
−β F[ρ,g,v,ϑ]
= e
−β F
U
[ρ]
. (A6.1.54)
By suitably choosing the dynamics of the field ϑ, the equations of motion for {ρ,g, v} are
kept unchanged and decoupled from that for ϑ. Thus, the dynamics at the level of ρ,g, and
v remains the same even though the equilibrium distribution is renormalized. This choice,
however, cannot be considered definitive. The lack of uniqueness in the problem is also
seen from the fact that a transformation F [ρ,g,v,ϑ]→F [ρ,g,v,ϑ]−μ
6
dx ρ(x),
where μ is a constant, leaves the equations for the dynamics invariant. The final equilib-
rium probability distribution of the coarse-grained fields is undetermined up to a factor of
exp{−μ
6
dx ρ(x)}. The dynamical equations do not uniquely determine ρ
0
.
7
Renormalization of the dynamics
We have discussed the construction of the nonlinear Langevin equations for the slow modes
in a number of different systems in the previous chapter. Next, we analyze how the non-
linear coupling of the hydrodynamic modes in these equations of motion affects the liquid
dynamics. In particular, we focus here on the case of a compressible liquid in the super-
cooled region. In this book we will primarily follow an approach in which the effects of
the nonlinearities are systematically obtained using graphical methods of quantum field
theory. Such diagrammatic methods have conveniently been used for studying the slow
dynamics near the critical point (Kawasaki, 1970; Kadanoff and Swift, 1968) or turbulence
(Kraichnan 1959a, 1961a; Edwards, 1964). The present approach, which is now standard,
was first described by Martin, Siggia, and Rose (1973). The Martin–Siggia–Rose (MSR)
field theory, as this technique is named in the literature, is in fact a general scheme applied
to compute the statistical dynamics of classical systems.
The field-theoretic method presented here is an alternative to the so-called memory-
function approach. The latter in fact involves studying the dynamics in terms of non-
Markovian linearized Langevin equations (see, for example, eqn. (6.1.1) which are obtained
in a formally exact manner with the use of so called Mori–Zwanzig projection operators.
This projection-operator scheme is described in Appendix A7.4). The generalized trans-
port coefficients or the so-called memory functions in this case are frequency-dependent
and can be expressed in terms of Green–Kubo forms of integrals of time correlation func-
tions. These memory functions account for the long-time effects, i.e., the role of correlated
dynamics of the particles in the dense fluid. The renormalized perturbation expression for
the memory function finally leads us to the model for the slow dynamics characteristic of
the dense liquid. The latter is termed the mode-coupling theory (MCT) for liquids and has
proved to be an essential tool for understanding the slow dynamics in a metastable liquid
below the freezing point T
m
. The evaluation of the memory function in terms of correla-
tion functions using the projection-operator method is also presented in the appendix. This
approach, though somewhat ad hoc, is often taken as an alternative way of obtaining the
self-consistent mode-coupling model.
The MSR field-theory approach discussed below is particularly aimed towards analyz-
ing the full implications of the nonlinearities in the equations of generalized hydrody-
namics introduced in Section 6.2.1. These fluctuating nonlinear Langevin equations are
318
7.1 The Martin–Siggia–Rose theory 319
Markovian. The random forces or the noises in the nonlinear stochastic equations of motion
are related to the bare transport coefficients of the system through the usual fluctuation–
dissipation relations.
1
The corrections to the bare transport coefficients due to the nonlin-
earities provide what is termed the mode-coupling contributions. With the field-theoretic
methods described below, these corrections can be computed in a systematic manner in
successive orders in a perturbation theory. Finally, apart from the above two approaches,
the simplest form of the mode-coupling model is also obtained directly from the equations
of nonlinear fluctuating hydrodynamics without getting into an involved formalism. We
present this deduction (Kawasaki, 1995) in Appendix A7.
7.1 The Martin–Siggia–Rose theory
The MSR theory is constructed in terms of a generating functional from which both the
time correlation and the response functions are obtained. The original theory (Martin et al.,
1973; Dekker and Haake, 1975; Phythian, 1975, 1976; Andersen, 2000) was developed
with an operator formalism involving the field ψ and an additional adjoint operator
ˆ
ψ.
The ψ operator does not commute with its hatted counterpart. The correlation between
ψ and
ˆ
ψ corresponds to the response functions, which are computed together with the
usual correlation functions between the ψ s. The MSR field theory applied to the case of
classical continuous fields satisfying a linear or nonlinear Langevin equation has subse-
quently been formulated using the functional integral approach (Janssen, 1976; Bausch
et al., 1976; Phythian, 1977; De Dominicis and Pelti, 1978). By construction this for-
mulation also involves, in addition to the field variable, an associated hatted field in a
manner that is very similar to the operator approach of the original MSR theory. In the
following we will adhere to the functional integral formulation of the MSR. It has been
applied extensively in a variety of problems: to mention a few examples, for the study of
diffusion in disordered media (Bouchaud and Georges, 1990); polymer solution dynamics
(Fredrickson and Helfand, 1990); domain-growth problems in dynamics of phase transition
(Mazenko, 1990); diffusion in random media (Deem and Chandler, 1994); driven diffusive
systems (Garrido et al., 1990); diffusion of a Brownian particle in a fluid with random time-
independent velocity fields (Deem, 1995); critical dynamics of driven interfaces in random
media (Narayan and Fisher, 1993); interface growth using Kadar–Parisi–Zhang (Kadar
et al., 1986; Medina et al., 1989) equations in field-theoretic models (Sun and Plischeke,
1994; Frey and Tauber, 1994); dynamics of liquid crystals (Milner and Martin, 1986); study
of turbulence (Eyink, 1994; Mou and Weichman, 1995); and roughening surface transitions
in the presence of a disordered pinning potential (Scheidl, 1995). Our primary focus in the
present discussion is on the formulation of the MSR model for studying the dynamics of
supercooled liquids. The field-theoretic model for the dense liquid has been studied by var-
ious authors (Das and Mazenko, 1986, 2009; Kim and Mazenko, 1991, Mazenko and Yeo,
1994; Yeo and Mazenko, 1995, Das and Schilling, 1993, Kawasaki and Miyazima, 1997;
1
These bare transport coefficients L
0
ij
s introduced here are treated as input parameters to be determined from kinetic theories
dealing with the short-time dynamics of the fluid.

320 Renormalization of the dynamics
Kawasaki and Kim, 2001; Harbola and Das, 2002; Andreanov et al., 2006; Miyazaki and
Reichman, 2005; Kim and Kawasaki, 2008; Mazenko, 2010; Yeo, 2010). The formulation
of the MSR theory presented here gives rise in a very natural way to a model for the renor-
malized (due to the nonlinearities) liquid-state dynamics in a self-consistent form. As we
will see in the next chapter, this gives rise to the feedback mechanism of mode-coupling
theory (MCT) for slow dynamics.
Let us first outline the construction of the field-theoretic model for renormalization of
the dynamics of the compressible liquid (Das and Mazenko, 1986). The associated MSR
field theory involves two sets of fields {ρ,g, v} and their corresponding hatted counterparts
{ˆρ,
ˆ
g,
ˆ
v}. The noise-averaged correlation functions of the field variables are expressed in
terms of generalized transport coefficients with wave-vector and frequency dependences.
Such dependences result in the MSR theory from the renormalization of the bare transport
coefficients due to the nonlinearities in the equations of motion. The corrections to the
transport coefficients are obtained as a perturbation series expansion involving graphs that
are evaluated in terms of correlation and response functions. For a dense liquid approach-
ing the glass transition, the evaluation of the perturbation series for the transport coef-
ficient is done assuming that the effects of coupling of strong density fluctuations are
dominant.
7.1.1 The MSR action functional
Let us begin with a field ψ whose dynamics is given by the stochastic equation of motion,
∂ψ(1)
∂t
1
=−{U
1
[1]+U
2
[1
¯
2]ψ(
¯
2) +U
3
[1
¯
2
¯
3]ψ(
¯
2)ψ(
¯
3)}+θ(1)
≡−W [ψ]+θ(1). (7.1.1)
In the above equation the numbers 1,
¯
2,... etc. label space, time, and any other index
associated with the fields {ψ} representing the slow variables. In eqn. (7.1.1) it is implied
that the repeated barred indices are integrated or summed over. The noise θ is assumed to
be simply additive. The correlation of the noise is defined in terms of the matrix L
0
of bare
or short-time kinetic coefficients for the system,
θ(1)θ(2)=2k
B
TL
0
(1, 2). (7.1.2)
The above description of the dynamics can be generalized to the case in which the noise
is multiplicative (Jensen, 1981). The functional f [ψ] of the field ψ which satisfies the
equation of motion (7.1.1) is formally written in the form
f [ψ]=
Dψ
δ(ψ − ψ
) f [ψ
], (7.1.3)
