Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond
Подождите немного. Документ загружается.


6.1 Nonlinear Langevin equations 281
The dynamic part
Let us now consider the dynamic part K
(d)
φ
¯
φ
(z) of the memory function given by (6.1.35).
This part is in general frequency-dependent and is considerably more complicated. From
our discussion in the previous section on the memory function it is known that the linear
part of the dynamics of the collective variables {
ˆ
φ
i
} does not contribute to this part. In
the present chapter we treat this part within the framework of the Markov approximation.
We will work with the assumption that the dynamic part of the memory function depends
only on the fast variables in the system. At the formal level the expression on the RHS of
(6.1.35) simplifies to the following form on using the result (6.1.38) for Lg
φ
:
K
(d)
φφ
(z)P[φ
]≡
ij
∂
∂φ
i
∂
∂φ
j
ij
φφ
(z)
, (6.1.52)
where
ij
φφ
(z) is a functional of φ and φ
. In reaching the expression on the LHS of eqn.
(6.1.52) the diagonal property of the static correlation S
¯
φφ
is used in a manner similar to
what has been done in the case of the static part. We finally obtain
K
(d)
φ
¯
φ
(z)S
¯
φφ
≡
D(
¯
φ)K
(d)
φ
¯
φ
(z)δ(
¯
φ − φ
)P[φ
]
= K
(d)
φφ
(z)P[φ
]. (6.1.53)
A detailed expression for
ij
φφ
(z) may be obtained from the defining relation (6.1.35)
for the dynamic part K
(d)
φφ
of the memory function. However, in the present discussion of
the dynamics of the many-particle system using the nonlinear fluctuating-hydrodynamics
approach we treat this dynamic part in an indirect manner. We approximate the dynamic
component of the memory function only in terms of the short-time dynamics of the system.
The Markov approximation
In the simplest approximation the matrix elements
ij
φφ
(z) are assumed to be frequency-
independent and are obtained in terms of the short-time transport coefficients of the system.
In Section 5.3.1 we have shown in eqn. (5.3.48) that for the linear Langevin equation the
correlation of the noise, which is assumed orthogonal to the slow modes, is obtained in
terms of the dynamic part of the memory function. On applying this in the present context
for the Langevin equation (6.1.33), the noise correlation satisfies
f
φ
(t) f
φ
(t
)=K
(d)
φφ
(t − t
)P[φ
]
= 2i
ij
∂
∂φ
i
∂
∂φ
j
ij
φφ
δ(t − t
). (6.1.54)
To obtain the RHS we have taken the inverse Laplace transform of (6.1.52) to obtain
K
(d)
φφ
(t − t
). In the fluctuating-hydrodynamics approach these short-time transport coeffi-
cients denoted by L
0
ij
act as phenomenological inputs in the theory and may be determined
from a detailed microscopic kinetic-theory approach to the system’s dynamics. The bare

282 Nonlinear fluctuating hydrodynamics
kinetic coefficients L
0
ij
(φ) in general can depend on the field φ. We assume as a defining
relation
ij
φφ
=−iβ
−1
L
0
ij
(φ)δ(φ − φ
)P[φ
], (6.1.55)
which is designed so that the contribution from the dynamic part of the memory function
represents dissipation. L
0
ij
(φ) is the matrix of generalized transport coefficients for the
system. The frequency-independent form of the dynamic part influences the construction
of the linear Langevin equation for g
φ
(t) in two important ways.
(1) The correlation of the noise f
φ
of the Langevin equation (6.1.33) is now given by
f
φ
(t) f
φ
(t
)=K
(d)
φφ
(t − t
)P[φ
]
= 2β
−1
ij
∂
∂φ
i
∂
∂φ
j
#
L
0
ij
(φ)δ(φ − φ
)P[φ
]
$
δ(t − t
). (6.1.56)
(2) The ansatz (6.1.55) for the dynamic part of the memory function is useful in expressing
the corresponding contribution in the Langevin equation (6.1.33) (given by the third
term on the LHS of this equation) in terms of the bare transport coefficients L
0
ij
.On
substituting this ansatz into (6.1.55) we obtain for K
(d)
φ
¯
φ
(z)
K
(d)
φφ
(z)P[φ
]=−iβ
−1
ij
∂
∂φ
i
∂
∂φ
j
L
0
ij
(φ)δ(φ − φ
)P[φ
]
=−iβ
−1
ij
∂
∂φ
i
L
0
ij
(φ)
&
∂
∂φ
j
δ(φ − φ
)
'
P[φ
]+δ(φ − φ
)
∂ P[φ
]
∂φ
j
= iβ
−1
ij
∂
∂φ
i
L
0
ij
(φ)
∂
∂φ
j
δ(φ − φ
) + β
∂ F[φ]
∂φ
j
δ(φ − φ
)
P[φ
].
(6.1.57)
On canceling out the common factor of P[φ
] from both sides of (6.1.57) we obtain
the result
K
(d)
φφ
(z) = iβ
−1
ij
∂
∂φ
i
L
0
ij
(φ)
β
∂ F[φ]
∂φ
j
+
∂
∂φ
j
δ(φ −
¯
φ)
= iβ
−1
ij
∂
∂φ
i
#
L
0
ij
(φ)
˜
D
( j)
φ
δ(φ −
¯
φ)
$
. (6.1.58)
Using the result (6.1.58) in the dynamic part of the memory function, the third term on
the LHS of the linear Langevin equation (6.1.33) for g
φ
(t) reduces to
iK
(d)
φ
¯
φ
g
¯
φ
(t) =−β
−1
ij
∂
∂φ
i
#
L
0
ij
(φ)
˜
D
( j)
φ
δ(φ −
¯
φ)g
¯
φ
(t)
$
=−β
−1
ij
∂
∂φ
i
L
0
ij
(φ)
˜
D
( j)
φ
g
φ
(t), (6.1.59)
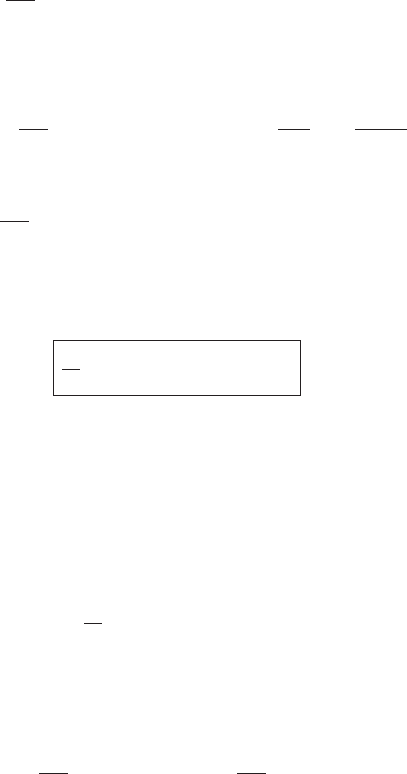
6.1 Nonlinear Langevin equations 283
with the L
0
ij
(φ) being bare kinetic coefficients defining the correlation of the noise
f
φ
(t) through eqn. (6.1.56).
The Fokker–Planck equation
On adding the static and dynamic parts given by (6.1.51) and (6.1.59), respectively, we
obtain for the contribution of the memory function to the Langevin equation
iK
φ
¯
φ
g
¯
φ
(t) = i
K
(s)
φ
¯
φ
+ K
(d)
φ
¯
φ
g
¯
φ
(t)
=
i
∂
∂φ
i
⎡
⎣
V
i
[φ]−β
−1
ij
L
0
ij
(φ)
˜
D
( j)
φ
⎤
⎦
g
φ
(t) ≡−D
φ
g
φ
(t), (6.1.60)
where the operator D
φ
is defined as
D
φ
=−
i
∂
∂φ
i
⎡
⎣
V
i
[φ]−β
−1
j
L
0
ij
(φ)
∂
∂φ
j
+ β
∂ F[φ]
∂φ
j
⎤
⎦
=
i
∂
∂φ
i
⎡
⎣
V
i
[φ]−β
−1
j
L
0
ij
(φ)
˜
D
( j)
φ
⎤
⎦
. (6.1.61)
On substituting the result (6.1.60) into the generalized Langevin equation (6.1.33) for
g
φ
(t), the latter reduces to the form
∂
∂t
g
φ
(t) = D
φ
g
φ
(t) + f
φ
(t). (6.1.62)
The above equation is a generalized form of the Fokker–Planck equation (Fokker, 1914;
Planck, 1917; Risken, 1996) with noise f
φ
whose correlation is given by (6.1.56) in terms
of the bare kinetic coefficients. This is the key result of the present section and is essential
in obtaining the nonlinear Langevin equation for the collective variables.
The average quantity g
φ
(t) represents the probability that the collective modes {
ˆ
φ
i
}
have the value {φ
i
}. Taking the average of (6.1.62) and using (6.1.27) gives a Fokker–
Planck equation:
∂
∂t
g
φ
(t)=D
φ
g
φ
(t) (6.1.63)
with D
φ
as the corresponding driving operator. For the equilibrium state, g
φ
(t)≡P[φ]
do not have any explicit time dependence, so D
φ
g
φ
(t)=0. Indeed, this equation is
satisfied by P[φ], as can be seen from direct substitution. Using (6.1.61) we have
D
φ
P[φ]=−
i
∂
∂φ
i
{
V
i
[φ]P[φ]
}
+ β
−1
∂
∂φ
i
j
L
0
ij
(φ)
˜
D
( j)
φ
P[φ], (6.1.64)
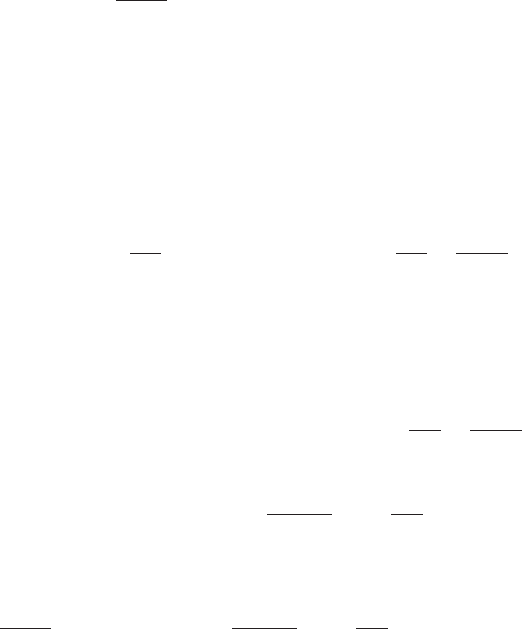
284 Nonlinear fluctuating hydrodynamics
where the operator D
φ
is as defined in (6.1.61).Using(6.1.46) and (6.1.49),theRHSof
(6.1.61) is equal to zero.
The nonlinear Langevin equation
To summarize the discussion so far, we have reached a linear Langevin equation (6.1.62)
for the collective variable g
φ
(t) defined through the relation (6.1.10). The dynamics is
assumed to have a clear difference in the time scale for the collective modes and that for
the noise f
φ
. The correlation of the noise is given in eqn. (6.1.56) by the short-time trans-
port coefficients L
0
ij
. A set of nonlinear Langevin equations for the slow modes {
ˆ
φ
i
(t)} is
obtained by integrating (6.1.62) with respect to the function {φ
i
}. Considering the equation
for the collective variable
ˆ
φ
i
, we note that
ˆ
φ
i
(t) =
D(φ)φ
i
g
φ
(t). (6.1.65)
On taking the first moment of eqn. (6.1.62) we obtain the nonlinear Langevin equation,
∂
ˆ
φ
i
(t)
∂t
=
D(φ)φ
i
D
φ
g
φ
(t) + θ
i
(t). (6.1.66)
The noise θ
i
(t) is obtained from the first moment of f
φ
as
θ
i
(t) =
D(φ)φ
i
f
φ
. (6.1.67)
The first term on the RHS of (6.1.66) is given by
D(φ)φ
i
D
φ
g
φ
(t)
=−
D(φ)φ
i
j
∂
∂φ
j
V
j
[φ]−
k
L
0
jk
(φ)
β
−1
∂
∂φ
k
+
∂ F[φ]
∂φ
k
g
φ
(t).
(6.1.68)
Upon integrating by parts with the derivative ∂/∂φ
j
acting on φ
i
on the RHS, eqn. (6.1.68)
reduces to the form
D(φ)φ
i
D
φ
g
φ
(t) =
D(φ)
⎡
⎣
V
i
[φ]−
j
L
0
ij
(φ)
β
−1
∂
∂φ
j
+
∂ F[φ]
∂φ
j
⎤
⎦
g
φ
(t)
= V
i
[
ˆ
φ]+
j
β
−1
∂ L
0
ij
(
ˆ
φ)
∂
ˆ
φ
j
− L
0
ij
∂ F
∂
ˆ
φ
j
. (6.1.69)
The corresponding Langevin equation is given by
∂
ˆ
φ
i
(t)
∂t
= V
i
[
ˆ
φ]+
j
β
−1
∂ L
0
ij
(
ˆ
φ)
∂
ˆ
φ
j
− L
0
ij
∂ F
∂
ˆ
φ
j
+ θ
i
(t). (6.1.70)

6.1 Nonlinear Langevin equations 285
The correlation of the noise θ
i
(t) is computed from the definition (6.1.67) as
θ
i
(t)θ
j
(t
)=
D(φ)
D(φ
)φ
i
φ
j
f
φ
(t) f
φ
(t
). (6.1.71)
UsingontheRHSofeqn. (6.1.72) the ansatz (6.1.56) which defines the correlation of the
noise f
φ
in terms of the bare transport coefficients L
0
ij
, it reduces to the following relation
θ
i
(t)θ
j
(t
)
= 2β
−1
D(φ)D(φ
)φ
i
φ
j
kl
∂
∂φ
k
∂
∂φ
l
#
L
0
kl
(φ)δ(φ − φ
)P[φ
]
$
δ(t − t
). (6.1.72)
On partially integrating (6.1.72) we obtain,
θ
i
(t)θ
j
(t
)=2β
−1
D(φ)D(φ
)
#
L
0
ij
(φ)δ(φ − φ
)P[φ
]
$
δ(t − t
)
= 2β
−1
D(φ)L
0
ij
(φ)P[φ]δ(t − t
)
= 2β
−1
1
L
0
ij
(φ)
2
δ(t − t
), (6.1.73)
where
1
L
0
ij
(φ)
2
denotes the equilibrium averaged form of the matrix of the bare transport
coefficients.
For the somewhat simplified case in which the dependence of the bare transport coef-
ficients on the slow modes
ˆ
φ
i
is ignored, we obtain from (6.1.71) the nonlinear Langevin
equation for the dynamics of the slow variables {
ˆ
φ
i
},
∂
ˆ
φ
i
(t)
∂t
= V
i
[
ˆ
φ]−
j
L
0
ij
∂ F
∂
ˆ
φ
j
+ θ
i
(t), (6.1.74)
where (a) F is the equivalent Hamiltonian for the system expressed as a functional of
the slow modes {
ˆ
φ
i
} such that the equilibrium distribution function at temperature T is
P[φ]=Z
−1
exp[−F/(k
B
T )], (b) the streaming current V
i
is given by (6.1.48), and (c) the
correlation of the noise θ
i
(t) is given by
θ
i
(t)θ
j
(t
)=2k
B
TL
0
ij
δ(t − t
) (6.1.75)
in terms of the matrix of bare transport coefficients L
0
ij
. Similarly to the case of the
linearized Langevin equation, the first and second terms on the RHS of (6.1.75) have oppo-
site signatures with respect to the time reversal. The above Langevin equation is further
simplified to the form
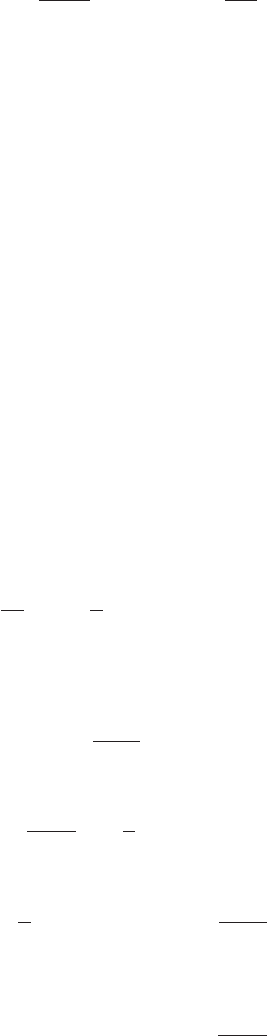
286 Nonlinear fluctuating hydrodynamics
∂
ˆ
φ
i
(t)
∂t
=
Q
ij
− L
0
ij
δF
δψ
j
, (6.1.76)
where the second term on the RHS of eqn. (6.1.48) has been ignored.
(i) From the definition of the Poisson bracket it follows that Q
ij
(−t) =−
i
j
Q
ij
(t),
where
i
denotes the time-reversal property of the slow mode
ˆ
φ
i
, i.e.,
ˆ
φ
i
(−t) =
i
ˆ
φ
i
(t). It follows from the expression (6.1.48) for V
i
that this part of the equation of
motion for
ˆ
φ
i
remains invariant under time reversal. Hence V
i
represents the reversible
part of the dynamics.
(ii) Assuming that the matrix L
0
ij
satisfies under time reversal the property
L
0
ij
(−t) =
i
j
L
0
ij
(t), (6.1.77)
the second term on the LHS of (5.3.51) breaks the reversal symmetry of the equation
of motion and hence represents dissipation.
The Gaussian noise
The noise correlation given by (6.1.76) for the case of the bare-transport-coefficient matrix
L
0
ij
is independent of the slow variables
ˆ
φ and in fact corresponds to the noise θ
i
having a
Gaussian distribution function. Thus the average of a dynamic variable A[θ] with respect
to the noise is defined as
A[θ] =
D(θ) A[θ ]P[θ ], (6.1.78)
where the Gaussian distribution function P[θ] for the noise is given by
P[θ]=
1
Z
θ
exp
⎡
⎣
−
β
4
ij
+∞
−∞
d
¯
t θ
i
(
¯
t)[L
0
]
−1
ij
θ
j
(
¯
t)
⎤
⎦
. (6.1.79)
Z
θ
is a normalization constant so as to ensure that
6
D(θ)P[θ]=1. In order to compute
the noise correlation with respect to P[θ], we start from the functional identity
D(θ)
δ
δθ
i
(t)
{
P[θ]A[θ]
}
= 0. (6.1.80)
With the form (6.1.80) for P[θ ], its derivative with respect to the noise is given by
δ P[θ ]
δθ
i
(t)
=−
β
2
[L
0
]
−1
ik
θ
k
(t)P[θ]. (6.1.81)
The identity (6.1.81) then implies
β
2
[L
0
]
−1
ik
θ
k
(t) A[θ ] =
-
δ A[θ]
δθ
i
(t)
.
. (6.1.82)
On multiplying eqn. (6.1.83) by the matrix L
0
from the left we obtain the equivalent
relation
θ
i
(t) A[θ ] = 2β
−1
L
0
ik
-
δ A[θ]
δθ
k
(t)
.
. (6.1.83)

6.2 The compressible liquid 287
Now, on choosing A[θ]≡θ
j
(t
), we obtain
θ
i
(t)θ
j
(t
)=2β
−1
L
0
ik
-
δθ
j
(t
)
δθ
k
(t)
.
= 2β
−1
L
0
ij
δ(t − t
), (6.1.84)
which is the same as (6.1.76) obtained above. In all subsequent treatment of the fluctuat-
ing hydrodynamics in this book we confine the discussion to the case of Gaussian white
noise.
6.2 The compressible liquid
We consider an appropriate set of slow variables {
ˆ
φ
i
} for the compressible liquid and con-
struct the corresponding equations for the dynamics of these collective modes. These equa-
tions, which are generalizations of the corresponding macroscopic hydrodynamic laws, are
applied here to study phenomena at microscopic frequencies and wavelength. The collec-
tive modes are deviations from the equilibrium state whose properties are assumed to be
known. For the chosen set of variables there is a vast difference in the time scales of varia-
tion in comparison with that of the large number of microscopic variables of the fluid. The
origin of these slow variables for a specific system can vary, e.g., microscopic conserva-
tion laws as in the present case, the heavy mass of a Brownian particle or breaking of a
continuous symmetry (Forster, 1975) of a many-particle system. In the present chapter we
discuss the formulation of these nonlinear fluctuating equations for a few generic cases.
The fluctuating nonlinear Langevin equations for the liquid are Markovian in form and
involve bare transport coefficients related to the noise through a standard fluctuation–
dissipation relation,
∂
ˆ
φ
i
(r, t)
∂t
+ V
i
[
ˆ
φ]+
dr
j
L
0
ij
(r, r
)
∂ F
∂
ˆ
φ
j
(r
, t)
= θ
i
(r, t). (6.2.1)
The matrix of bare transport coefficients L
0
ij
of the liquid defines the correlation of the
noise θ
i
. The transport properties of the liquid for short times are determined by L
0
ij
.For
long-time dynamics the bare coefficients are renormalized due to the nonlinearities in the
equations of motion leading to generalized transport coefficients. In the theory we discuss
here the equations of nonlinear fluctuating hydrodynamics (NFH) are conveniently used
for computing the corrections to the linear model. Before we turn to the development of
the formalism for renormalization of the nonlinear theory in the next chapter, we obtain
the appropriate set of nonlinear fluctuating hydrodynamic equations for the compressible
liquid in the present chapter.
6.2.1 The one-component fluid
We consider the model for the compressible liquid with a set of slow variables consisting
of (a) the mass density ρ(r, t) and (b) the momentum density g(r, t) (Das and Mazenko,

288 Nonlinear fluctuating hydrodynamics
1986; Das, 1987, 1990). These collective densities are defined in terms of the phase-space
variables {r
α
, p
α
} as
ˆρ(x, t) =
α
mδ(x − r
α
), (6.2.2)
ˆ
g
i
(x, t) =
α
p
i
α
δ(x − r
α
). (6.2.3)
The energy fluctuations are ignored in the present analysis for simplicity. The nonlinear
Langevin equations for these slow variables are constructed using the standard prescrip-
tions given above in eqn. (6.2.1). The two main ingredients in reaching the nonlinear
equations of motion are the Poisson brackets and the coarse-grained free-energy functional.
The Poisson brackets
The reversible part of the generalized Langevin equation involves the classical Poisson
brackets Q
ij
. These are computed from the corresponding microscopic definitions (6.2.2)
of the respective slow modes in terms of the phase-space variables. Using the canonical
Poisson-bracket relation,
#
r
i
α
, p
j
β
$
= δ
ij
δ
αβ
, (6.2.4)
we obtain the following results for the Poisson brackets between hydrodynamic variables
in the one-component fluid:
{ˆρ(x), ˆρ(x
)}=0,
{ˆg
i
(x), ˆg
j
(x
)}=−∇
j
x
[δ(x − x
) ˆg
i
(x)]+∇
i
x
[δ(x − x
) ˆg
j
(x
)], (6.2.5)
{ˆρ(x), ˆg
i
(x
)}=−∇
i
x
[δ(x − x
) ˆρ(x)].
The Poisson brackets are by definition antisymmetric, Q
ij
=−Q
ji
.
The coarse-grained free-energy functional
In order to compute the reversible streaming-velocity terms as well as the dissipative terms,
we need the driving free-energy functional F[a]=F[ρ,g] as a functional of the coarse-
grained variables. In Appendix A6.1 we discuss the computation of F for the compressible
liquid as a functional of the coarse-grained densities. The functional dependence of F on
the hydrodynamic fields, i.e., ρ and g, is divided into two parts,
F[ρ, g]=F
K
[g,ρ]+F
U
[ρ]. (6.2.6)
The momentum-density-dependent kinetic part F
K
is obtained as
F
K
[g,ρ]=
dx
g
2
(x)
2ρ(x)
. (6.2.7)
The derivation of the kinetic part F
K
as given in eqn. (6.2.7) can also be obtained from a
microscopic approach (Langer and Turski, 1973) starting from a calculation of the

6.2 The compressible liquid 289
equilibrium partition function. This is discussed in Appendix A6.1. The potential part
F
U
of F is treated as a functional of the density ρ only. In Appendix A6.1 we have
discussed the simplest approximation in which F[ρ] is obtained from the bare particle
interactions as U[ρ]. In the following we discuss a scheme in which the F
U
[ρ] in terms of
the coarse-grained density ρ(x) is constructed by maintaining the analogy with the static
or thermodynamic description of the liquid. We use the mass density ρ(x) here instead
of the number density n(x). In order to be consistent with the discussions in the earlier
chapters and to avoid clutter, we take the two to be the same, i.e., the mass of the fluid par-
ticles m = 1. For the one-component system ρ(x) = mn(x). A simple way of constructing
the free-energy functional is to choose a form that preserves the static or the equal-time
correlation function in the equilibrium state. Consider a formal expansion for F
U
that is
quadratic in density fluctuations,
β F
U
=
1
2
dx
dx
δρ (x)M(x − x
)δρ(x
). (6.2.8)
The equal-time correlation of the density fluctuations at two different points is obtained
by taking an average over the function space with respect to the equilibrium distribution
exp[−F],
χ
ρρ
(x − x
) =δρ (x)δρ(x
)=
Dn δρ (x)δρ(x
)
e
−F
U
[ρ]
Z
N
, (6.2.9)
where Z
N
is the partition function defined as
Z
N
=
Dρ e
−F
U
[ρ]
. (6.2.10)
In order to compute the static correlation function χ
ρρ
, we use the functional identity
Dn
δ
δρ (x
)
ρ(x)
e
−β F
U
Z
N
= 0, (6.2.11)
to obtain the result
-
δρ (x)
δF
U
δρ (x
)
.
= δ(x − x
). (6.2.12)
δρ (x) =ρ(x) −ρ
0
denotes thedensity fluctuation. Usingeqn. (6.2.12) anddefinition (6.2.9),
we obtain M ≡χ
−1
ρρ
. The Gaussian expression (6.2.8) for the free-energy functional F
U
in
terms of the fluctuations of the coarse-grained density is therefore obtained in terms of
the static correlation function χ
ρρ
. For liquids supercooled below the freezing point it is
well known that there is no drastic change in the equal-time correlation function. Theories
of the liquid state can therefore be extended to metastable densities to compute the static
correlation function and the latter can be used as an input in the expression for F
U
.The
simplest choice for the correlation χ
ρρ
(x −x
) would be to take a completely uncorrelated
structure, i.e., ∼δ(x − x
), corresponding to a wave-vector-independent structure factor.
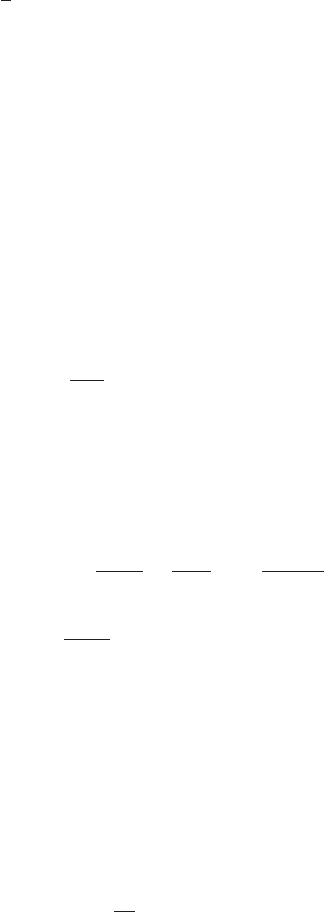
290 Nonlinear fluctuating hydrodynamics
However, at high density the structure is strongly correlated. Another possible choice for
the coarse-grained free-energy functional is to reproduce the first peak at wave vector
q =q
0
of the static structure factor in a Lorentzian form. This involves including terms
with the derivatives of density in F
U
,
β F
U
=
1
2
dx
A
0
δρ
2
(x) + κ
0
δρ (x)
#
∇
2
+q
2
0
$
2
δρ (x)
. (6.2.13)
The constants A
0
, κ
0
, and q
0
are temperature- and density-dependent fitting parameters to
match the static correlation functions (Das, 1987).
A more appropriate form of the coarse-grained free-energy functional is obtained by
making use of the expressions for the static correlations in terms of the Ornstein–Zernike
direct correlation function c(r). In the Fourier-transformed form, χ
nn
(k), or equivalently
the static structure factor S(k) defined in eqn. (1.2.79), relates to c(k) through the relation
(1.2.90). In general F
U
is split into an ideal-gas or entropic contribution F
id
and an inter-
action term F
in
(see Appendix A6.1). On expanding this entropic contribution in (A6.1.30)
to quadratic order in density fluctuations and using the relation (1.2.90) between S(k)
and c(k), we obtain the following expression for the interaction part of the free-energy
functional up to quadratic order of the coarse-grained density:
β F
in
[ρ]=−
1
2m
2
dx dx
c
(2)
(x − x
)δρ(x)δρ(x
). (6.2.14)
The coarse-grained free-energy functional F
U
[n] therefore takes the form referred to as the
Ramakrishnan–Yussouff form in Chapter 2. The total free energy is obtained as
F[ρ, g]=F
K
[ρ,g]+F
U
[ρ]
=
dx
g
2
(x)
2ρ(x)
+
ρ(x)
βm
ln
ρ(x)
3
0
m
− 1
−
1
2βm
2
dx dx
c
(2)
(x − x
)δρ(x)δρ(x
). (6.2.15)
The mode-coupling models for glassy dynamics in this book will be largely based on the
above Gaussian form of F
U
[ρ].
Langevin equations
Let us first consider the equation for mass density ρ(x, t). The momentum dependence of
F[ρ, g] is such that the continuity equation
∂ρ
∂t
+∇· g = 0 (6.2.16)
